网站地图
-
在数字全息显微中，相位信息被包裹在(-π，π]之间，称之为包裹相位，从包裹相位中提取实际相位的过程被称为相位解包裹[1]。相位解包裹是干涉测量法的许多应用中不可或缺的一步，如干涉合成孔径雷达[2]、核磁共振成像[3]、电子散斑模式干涉等[4]。但是，在实际情况中，存在诸如相位噪声、相邻像素之间相位不连续，以及相位混叠等问题，使得异常情况下的相位解包裹比较困难。
近年来，相位解包裹的算法可以分为以下几个方向：路径跟踪算法、最小范数法、时间相位展开法和基于深度学习的相位解包裹算法。其中路径跟踪算法又包括枝切法[5]、质量导向算法[6]、掩模切割算法[7]和最小不连续算法[8]等等。枝切法首先通过找到所有残差点[2]，将最近的两个正负极性残点以最近的路径连接起来，连接完所有的残差点后再任意选取一个非残差点作为起点，在不跨越残差点路径的条件下，沿着积分路径进行解包裹，然而在有大量残差点的情况下，残差点之间的路径可能会围成一个封闭环，使得解包裹不完全。质量导向法首先通过一种计算方法(如2阶相位差分[9]、相关系数、伪相关系数[1]等等)来生成质量图，接着按照每个像素点的质量从高到低依次进行解包裹，但是该方法比较依赖质量图的质量，解包裹性能不稳定。掩模切割法结合了前两种算法的优点，以残差点为起点，质量由低到高，形成掩模线，且线上所有残差点正负极性抵消，最后在不跨过掩模线的条件下进行积分，完成解包裹，它的缺点同样是需要高质量的质量图。最小不连续算法中将相邻像素的包裹相位值超过π定义为一个不连续，通过一个特定路线引导相位展开，使得最后不连续的总和最小，但是该算法需要占用较大的内存和较长的处理时间。
最小范数法的解包裹过程与路径无关，它是通过对代价函数的最小化来获得解包裹相位。当代价函数中的指数为2时，它也被称之为最小二乘法。最小二乘法的实质就是求解纽曼条件下的泊松方程[10]，它也可分为不带权重的最小二乘法和带权重的最小二乘法两种。前者可以通过基本迭代法、离散余弦变换或傅里叶变换来求解泊松方程；后者则是将质量图或掩模图等作为权重，以达到减小噪声和残点对解包裹的影响。
相对于空间相位解包裹算法对空间像素的依赖，时间相位解包裹算法和多幅不同频率图像的同一位置有关。它主要包括多频法相位解包裹[11]和多频外差法相位解包裹[12]等。多频法通过使用多个不同频率的条纹照射物体，并提取出它们的截断相位，频率最小的条纹周期会覆盖整个物体，使得该频率下的相位不需要被解包裹，最后依次解出其高频下的相位信息。多频外差法同样将不同频率的条纹照射到被测物体上，但它需要对两个不同频率的条纹做差，得到一个等效的差频相位，它的周期同样能覆盖住整个被测物体，所以不需要对此进行解包裹，便可以逐级展开高频相位。
由于在实际情况中存在严重噪声、噪声不连续、噪声混叠等影响，传统相位解包裹方法对这类问题的响应不太理想。随着神经网络的发展，它能在输入与输出之间建立新的映射关系，使得在极端情况下相位解包裹的性能更好。近年来，WANG等人[13]以U型网络(U-Net)和残差网络为基础构建了深度学习相位解包裹网络(deep learning phase unwrap-net work, DLPU-Net)，实现了从带有高斯噪声的包裹相位恢复出绝对相位的端到端方法。ZHOU等人[14]以U-Net为生成器、马尔可夫判别器(patch-generative adversial network, Patch-GAN)，构造了一步相位解包裹的端到端网络——相位解包裹生成对抗网络(phase unwrap-generative adversial network, PU-GAN)。FANG等人[15]通过融合dense卷积的条件生成对抗网络学习散斑包裹的相位和去噪后的解包裹相位之间的映射过程。SPOORTHI等人[16]提出的Phase-Net首次将标签设定为相位的包裹计数，将相位解包裹转化为了语义分割的问题；次年，他们[17]又在网络中加入了dense模块，并提出了新的损失函数，实现了从包裹相位图到包裹计数再到绝对相位的解包裹过程。CHEN等人[18]将MobilenetV3和注意力机制融入到U-Net中，多尺度卷积提升了模型的泛化性，注意力机制提高了网络的学习性能，实现了更具鲁棒性的数字全息解包裹。
深度学习方法需要大量的数据进行训练，为了克服该问题，本文中提出了一种改进的swin-UNet-denoise网络，可在小样本上得到较好的结果。对于网络的改动如下，在swin block中，首先将归一化层后置，其次用余弦相似度取代点积运算，最后用对数位置偏移代替相对位置偏移。在上采样模块中，融入反卷积。最后在300对小样本数据集上进行训练，得到的去噪结果再经由最小二乘法进行相位解包裹。
-
本文中使用的数据是在参考文献[19]的基础上再添加散斑噪声[20]形成的带有散斑噪声的包裹相位图。散斑的形成基于光学4f系统，在第一个透镜的后焦面插入一个半径为R的圆形膜片，用来控制散斑颗粒的大小。目标域的单点复振幅可以通过原始域的单点复振幅和点扩散函数的卷积获得。点扩散函数[20]如下式所示：
$ \begin{aligned} & P=-\frac{\mathrm{i}}{\lambda f} \exp \left(\frac{2 \mathrm{i} \mathtt{π} f}{\lambda}\right) \exp \left[\frac{\mathrm{i} \mathtt{π}}{\lambda f}\left(X^2+Y^2\right)\right] \times \\ & \iint U\left(x^{\prime}, y^{\prime}\right) \exp \left[-\frac{2 \mathrm{i} \mathtt{π}}{\lambda f}\left(x^{\prime} X+y^{\prime} Y\right)\right] \mathrm{d} x^{\prime} \mathrm{d} y^{\prime} \end{aligned} $
(1) 式中：P表示点扩散函数；λ是波长；f是透镜的焦距；i是虚数单位；X和Y分别是目标域上的横纵坐标；U(x′, y′)是4f系统中间位置隔膜的瞳孔函数[20]，x′和y′分别表示隔膜上的横纵坐标，当x′2+y′2≤R时，U(x′, y′)=1，否则为0。在4f系统的原始域分别建立一个“参考”散斑场和一个“变形”散斑场，经过点扩散函数后，最后计算两光场之间的相位差。
仿真图的具体步骤如下：(a)生成一个大小为320× 320的随机矩阵，截取矩阵中心的256×256的部分，以减小相位图中4个角上的统计平均梯度分布(statistical average gradient distribution，SAGD)值，并可以使得再经过网络后的图像相对于不进行截取的图像的平均总体误差有所减小[19]，设置相位值范围在35 pixels~40 pixels之间；(b)构建相位随机分布在(-π，π]范围内的参考散斑场，将先前的变形相位叠加在随机相位上构成“变形”散斑场，在经过点扩散函数后，将两光场的散斑相位差包裹即为所得的仿真图。
图 1是peaks函数在不同孔径大小下生成的不同散斑颗粒大小的包裹相位图。4个小图中，图像的分辨率是256 pixels×256 pixels；2，4，6分别表示隔膜上的孔径大小占整个隔膜的1/2、1/4和1/6。从图中可以看出，隔膜上的孔径越大，散斑颗粒越小，即孔径大小与散斑颗粒大小成反比。
图 1 包裹散斑相位图
Figure 1. Wrapped speckle phase diagram
-
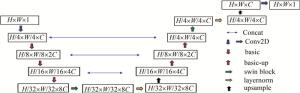
本文中提出的去噪算法是基于swin-UNet-denoise模型[21]，该算法是将swin block的思想和U-Net进行融合，将U-Net网络中实现特征提取模块的卷积方法替换为swin block中的窗口自注意力和滑动窗口自注意力。其中窗口自注意力将图像分成不同的图像块，接着在这些块中计算各自的注意力，其计算复杂度也只与窗口的大小有关。滑动窗口实现了不同图像块之间的交互，减少了不同图像块边缘之间的突兀，提升了模型的全局性。完整的模型结构如图 2所示。
图 2 Swin-UNet-dnoise模型
Figure 2. Swin-UNet-dnoise module
网络结构同U-Net较为相似，在编码器部分，下采样的过程中由basic模块代替卷积和池化，basic的结构图如图 3所示。
图 3 Basic模块
Figure 3. Basic module
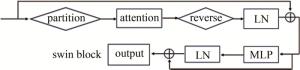
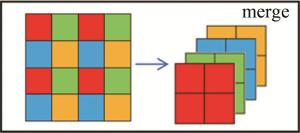
basic结构由8个swin block块和merge块构成。swin block的结构如图 4所示。图中LN(layer normalization)为层归一化。对输入的图像先进行分块操作，每个块的大小为窗口的大小，将分好块的图像进行窗口注意力和滑动窗口注意力的计算，再对计算完后的图像块进行复原，经过归一化层后结合残差与初始图像相加得到上半图的结果。多层感知器(multi-layer perceptron，MLP)模块包含两层全连接和激活函数。本文中用block V2结构[22]代替了原模型中的V1结构。不同之处在于：其一，将归一化层后置，使得不同层的激活值变得平稳；其二，用余弦相似度代替点积计算注意力以提升准确度；其三，用对数位置偏移代替相对位置偏移，使得即使在窗口变大时，在经过对数后，可以将空间范围减小。merge模块如图 5所示。将相同间隔的像素逐一取出，使得图像的大小减小，通道数增加，以此代替原来池化的作用。
图 4 Swin block模块
Figure 4. Swin block module
图 5 Merge模块
Figure 5. Merge module
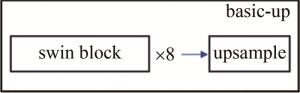
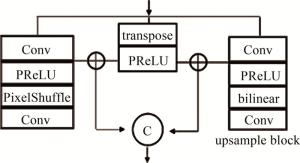
解码器部分由basic-up构成，结构如图 6所示。与basic相似，由8个swin block和上采样(upsample)组成。upsample的结构如图 7所示。图中，PreLU(parametric rectified linear unit)为带参数的线性整流单元[23]。上采样由3个部分组成，分别将输入的图像通过双线性插值法、PixelShuffle法和反卷积法。其中PixelShuffle法为merge模块的逆操作，将相邻通道的像素再合并到同一通道，3种方法分别将图像以不同的方式进行尺寸的扩展和通道的减少。区别于原模型，本文中将新增的反卷积先分别与另两种方法相结合，再将其在通道上进行合并，使得网络的精确性更高。
图 6 Basic-up模块
Figure 6. Basic-up module
图 7 上采样模块
Figure 7. Upsample module
跳跃连接部分与U-Net类似，连接编码器和解码器，将深层网络与浅层网络相结合，以防止网络的过拟合。合并后的高维图像再经过全连接将通道数复原。
-
由网络得到的去噪后的包裹相位再经过最小二乘法解得绝对相位。最小二乘法解包裹从包裹相位梯度出发，横向包裹梯度[24]Δgx如下式所示：
$ \Delta g^x=g(n+1, m)-g(n, m) $
(2) 式中：n和m分别表示图像像素的横纵坐标；g(n, m)为包裹相位值，即在图中(n，m)处的像素值。
纵向包裹梯度[24]Δgy如下式所示：
$ \Delta g^y=g(n, m+1)-g(n, m) $
(3) 最小二乘矩阵的求解方程[24]如下式所示：
$ \begin{gathered} \varPhi(n+1, m)+\varPhi(n-1, m)+\varPhi(n, m+1)+ \\ \varPhi(n, m-1)-4 \varPhi(n, m)=\Delta g^x(n, m)- \\ \Delta g^x(n-1, m)+\Delta g^y(n, m)-\Delta g^y(n, m-1) \end{gathered} $
(4) 式中：Φ(·)代表解包裹后的相位值。令等式右边等于ρ(n, m)，求解方程即为在纽曼边界条件下的离散泊松方程[24]，如式(5)和式(6)所示：
$ \frac{\Delta^2 \varPhi(n, m)}{\Delta n^2}+\frac{\Delta^2 \varPhi(n, m)}{\Delta m^2}=\rho(n, m) $
(5) $ \left\{\begin{array}{l} \Delta \varPhi^x(0, m)= \varPhi(1, m)-\varPhi(0, m)=0 \\ \Delta \varPhi^x(N, m)= \varPhi(N+1, m)-\varPhi(N, m)=0 \\ \quad\quad\quad\quad\quad\quad (m=1, \cdots, M) \\ \Delta \varPhi^y(n, 0)= \varPhi(n, 1)-\varPhi(n, 0)=0 \\ \Delta \varPhi^y(n, M)= \varPhi(n, M+1)-\varPhi(n, M)=0 \\ \quad\quad\quad\quad\quad\quad (n=1, \cdots, N) \end{array}\right. $
(6) 式中：ΔΦx和ΔΦy分别表示横向相位梯度和纵向相位梯度；矩阵网格的大小为N×M。将ρ通过离散余弦变换(discrete cosine transformation，DCT)转化为$ \hat{\rho}$，Φ在DCT域的精确解[24]如下式所示：
$ \hat{\varPhi}=\frac{\hat{\rho}}{2\left[\cos \left(\frac{\mathtt{π} n}{N}\right)+\cos \left(\frac{\mathtt{π} m}{M}\right)-2\right]} $
(7) 最后将$ \hat{\varPhi}$经过逆运算得到解包裹后的相位值。
-
本文中使用4种评价指标，结构相似度(structural similarity，SSIM)S如下式所示：
$ S=\frac{\left(2 \mu_1 \mu_2+C_1\right)\left(2 \sigma_{12}+C_2\right)}{\left(\mu_1{ }^2+\mu_2{ }^2+C_1\right)\left(\sigma_1{ }^2+\sigma_2{ }^2+C_2\right)} $
(8) 式中：μ1和μ2表示两幅图像的平均强度；σ1和σ2表示两幅图像的方差；σ12表示两幅图的协方差；C1和C2表示常数，用来起到避免分母为零和保持方程的稳定性的作用。结构相似度的值越大，代表两幅图像的相似度越高。
峰值信噪比(peak signal-to-noise ratio，PSNR)R如下式所示：
$ R=10 \lg \left(\frac{P^2}{E^2}\right) $
(9) 式中：P为图片像素中的最大像素值；E是两张图像的均方根误差，且$ E=\frac{1}{T} \sum\limits_{i=1}^T(W(i)-U(i))^2$；T代表总像素个数；i代表某个像素；W代表包裹图像的像素值；U代表解包裹图像的像素值。
均方根误差(root mean square error，RMSE)M如下式所示：
$ M=\sqrt{E} $
(10) 平均绝对误差(mean absolute error，MAE)A如下式所示：
$ A=\frac{1}{z} \sum\left|Y_i-X_i\right| $
(11) 式中：z为图像数量；Yi和Xi分别代表预测值和真值。MAE的值越小，代表两幅图像之间的差异也就越小。
-
实验使用CPU为12th Gen Intel(R) Core(TM) i5-12500H，RAM为16 GB，GPU为NVIDIA GeForce RTX 3050，显存4 G的计算机对图像进行处理。为了证明本文中的模型即使在面对少量样本时也依然可以得到较好的去噪结果，训练数据集一共只采用300组相位图像，其中3种不同散斑颗粒大小各占100组同时放入网络训练，使得网络对不同噪声影响的包裹相位图都能有积极的响应。测试集占训练集比重的20%，共60组数据。每张图像的分辨率皆为256 pixels×256 pixels。相位的最高高度随机分布在35 pixels~ 40 pixels之间，相位图的最低高度为0 pixel。
-
先对比了改进前后模型的去噪能力，本文中共进行了3种模型的实验对比，分别为原模型、将原模型中swin block V1模块替换为V2以及同时替换为V2和上采样模块的模型。图 8和图 9的折线图表明，3种网络在训练过程中，本文中提出的网络对验证集的去噪指标也普遍高于另两种网络，在100轮次时趋于收敛。
图 8 训练过程中3种网络对验证集的峰值信噪比的变化
Figure 8. Change of the peak signal-to-noise ratio of three kinds of networks to the verification set during training
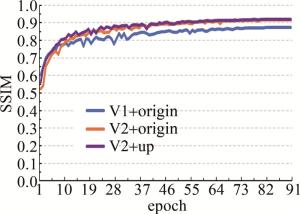
图 9 训练过程中3种网络对验证集的结构相似度的变化
Figure 9. Change of structural similarity of three kinds of networks to verification set during training
图 10为不同散斑噪声影响下，3种模型的去噪效果。在孔径为隔膜的1/2，即256/2 pixels时，由于此时噪声较小，所以3种网络去噪后的结果较为接近。当孔径为隔膜的1/4，即256/4 pixels时，可以发现V1+origin图像的最右侧，密集条纹发生了混叠的现象，但经过改进的网络后在V2+up中得到了改善，密集条纹的轮廓变得尤为清晰。当孔径只有隔膜的1/6，即256/6 pixels时在V1+origin的上侧更能清晰地看到这一混叠现象，而在V2+up中也得到了改善。
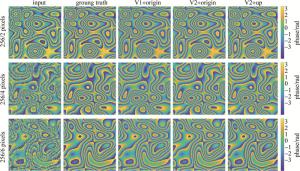
图 10 3种网络对于3种不同散斑程度相位图的去噪结果
Figure 10. Denoising results of three kinds of networks for three different speckle degree phase graphs
此外，可以从柱状图(见图 11和图 12)中看到不同散斑和不同网络之间的比较，且本文中所提出的网络的均方根误差和平均绝对误差最小。尤其是当V1模块替换成V2模块时，指标得到了大幅的提升。
图 11 3种网络在不同散斑噪声下的均方根误差
Figure 11. Root mean square error of three kinds of networks under different speckle noise
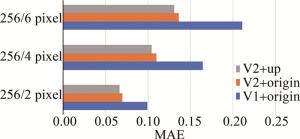
图 12 3种网络在不同散斑噪声下的平均绝对误差
Figure 12. Average absolute error of three kinds of networks under different speckle noise
随着散斑程度的增加，各个网络的指标也逐渐下降，在一些包裹条纹密集的地方，尤其是对于原先网络而言，相位条纹并没有完全复原，但所提网络得到的包裹相位条纹明显优于原网络，并且其指标依旧高于其它两个网络。表 1中是不同网络下对3种散斑噪声同时进行去噪时的平均值。本文中所提网络的指标有着明显的优势。
表 1 3种网络对测试集的评价指标的平均值
Table 1. Average value of the evaluation indexes of the three networks on the test set
mean SSIM PSNR RMSE MAE V1+origin 0.8803 20.4403 0.6196 0.1582 V2+origin 0.9211 22.2151 0.5053 0.1054 V2+up 0.9241 22.3827 0.4951 0.1005 -
经过本文作者提出的网络进行去噪后，将图像用最小二乘法求解，由于得到的结果在一些相位跳跃的位置过渡不平滑，所以将结果再经过中值滤波器，以此消除过渡不平滑的像素。此外，在解包裹阶段本文中方法与最小二乘法、PU-GAN和DLPU-Net法进行横向对比，对于深度学习方法训练集的数量都统一控制在300组数据集，得到的解包裹结果如图 13所示。其中最小二乘法在噪声较小时依稀可以看到模糊的相位，PU-GAN生成的图像带有类似棋盘效应的结果，使得分辨率较低，一步相位法在相位深度上与标签对比图有一定的差距。接着对测试集中图像的平均指标做出统计，如表 2所示。本文中提出的方法在4种指标上都明显优于其它3种方法。
图 13 不同方法对不同噪声程度的解包裹结果
Figure 13. Unwrapping results of different methods with different noise levels
表 2 不同方法得到的解包裹结果的评价指标
Table 2. Evaluation indexes of unwrapping results obtained by different methods
SSIM PSNR RMSE MAE least square 0.5344 9.6771 13.5715 12.0839 PU-GAN 0.9309 23.7721 3.0579 2.1431 DLPU-Net 0.9504 23.6297 3.0464 2.5411 propose 0.9977 39.9847 0.4864 0.4302 -
通过两步法进行散斑相位解包裹，散斑包裹相位先通过改进的swin-UNet-denoise网络进行去噪，再将去噪后的包裹相位通过最小二乘法获得绝对相位，最后通过中值滤波对图像进行平滑处理。实验结果表明，本文中的方法相较于其它几种方法具有较大的优势，分别在结构相似度、峰值信噪比、均方根误差和平均绝对误差上得到了较大的提升，并成功实现了从包裹散斑相位图的去噪并解包裹，且克服了深度学习需要大量训练集进行训练的缺点。由于难以获得真实的散斑相位图，故本文中使用模拟仿真的散斑包裹相位图进行训练和测试，可能对真实的散斑包裹相位图的解包裹性能有所下降。未来若是能收集足够的真实相位进行训练，相信能得到更具鲁棒性和泛化性的深度模型。
基于swin-UNet-denoise和最小二乘法的两步相位解包裹
Two-step phase unwrapping based on swin-UNet-denoise and least square method
-
摘要: 相位解包裹在众多领域应用中都占有重要地位，但总会受到噪声的影响，尤其是散斑噪声。为了去除散斑噪声对包裹相位图的影响，并从中恢复出实际的相位值，采用两步法进行了理论分析和实验论证，从不同程度散斑噪声包裹的相位中恢复出绝对相位。以swin-UNet-denoise网络为基础，将swin block中的归一化层后置，并用余弦相似度计算注意力值，然后将相对位移偏移替换为对数位置偏移，并在上采样模块融合反卷积层以此提升网络的去噪能力；将去噪结果通过最小二乘法解包裹，再通过中值滤波获得绝对相位。结果表明，结构相似度为99.77%，峰值信噪比为39.98，均方根误差为0.4864，平均绝对误差为0.4302。所有网络只在300组仿真数据集上进行训练验证，证明即使在小样本的条件下，该研究也能为更快速、更高效、更准确地实现带有散斑噪声的相位解包裹提供参考。Abstract: Phase unwrapping plays an important role in many applications, but it is always affected by noise, especially speckle noise. In order to remove the effect of speckle noise on the wrapping phase diagram, the actual phase value was recovered from it. The two-step method was used to make theoretical analysis and experimental demonstration, and the absolute phase was recovered from the phase covered by speckle noise in different degrees. In the first step, based on the swin-UNet-denoise network, the normalized layer in swin block was set back, and the attention value was calculated by cosine similarity. Then, the relative displacement offset was replaced by logarithmic position offset, and the deconvolution layer was fused in the upsampling module to improve the denoising ability of the network. In the second step, the denoising result was unwrapped by least square method, and then the absolute phase was obtained by median filtering. The results show that the structural similarity is 99.77%, the peak signal-to-noise ratio is 39.98, the root-mean-square error is 0.4864, and the average absolute error is 0.4302, respectively. In addition, all the networks are only trained and verified on 300 simulation data sets, which proves that the research can provide a reference for faster, more efficient and accurate phase unwrapping with speckle noise even under the condition of small samples.
-
Key words:
- holography /
- phase unwrapping /
- deep learning /
- least square method
-
图 8 训练过程中3种网络对验证集的峰值信噪比的变化
Figure 8. Change of the peak signal-to-noise ratio of three kinds of networks to the verification set during training
图 9 训练过程中3种网络对验证集的结构相似度的变化
Figure 9. Change of structural similarity of three kinds of networks to verification set during training
图 10 3种网络对于3种不同散斑程度相位图的去噪结果
Figure 10. Denoising results of three kinds of networks for three different speckle degree phase graphs
图 11 3种网络在不同散斑噪声下的均方根误差
Figure 11. Root mean square error of three kinds of networks under different speckle noise
图 12 3种网络在不同散斑噪声下的平均绝对误差
Figure 12. Average absolute error of three kinds of networks under different speckle noise
图 13 不同方法对不同噪声程度的解包裹结果
Figure 13. Unwrapping results of different methods with different noise levels
表 1 3种网络对测试集的评价指标的平均值
Table 1. Average value of the evaluation indexes of the three networks on the test set
mean SSIM PSNR RMSE MAE V1+origin 0.8803 20.4403 0.6196 0.1582 V2+origin 0.9211 22.2151 0.5053 0.1054 V2+up 0.9241 22.3827 0.4951 0.1005 
下载: 导出CSV
表 2 不同方法得到的解包裹结果的评价指标
Table 2. Evaluation indexes of unwrapping results obtained by different methods
SSIM PSNR RMSE MAE least square 0.5344 9.6771 13.5715 12.0839 PU-GAN 0.9309 23.7721 3.0579 2.1431 DLPU-Net 0.9504 23.6297 3.0464 2.5411 propose 0.9977 39.9847 0.4864 0.4302
下载: 导出CSV
-
[1] GHIGLIA D C, PRITT M D. Two-dimensional phase unwrapping: Theory, algorithms, and software[M]. New York: Wiley, 1998: 1-59. [2] YU H, LAN Y, YUAN Z, et al. Phase unwrapping in InSAR: A review[J]. IEEE Geoscience and Remote Sensing Magazine, 2019, 7(1): 40-58. doi: 10.1109/MGRS.2018.2873644 [3] SONG S M, NAPEL S, PELC N J, et al. Phase unwrapping of MR phase images using Poisson equation[J]. IEEE Transactions on Image Processing: A publication of the IEEE Signal Processing Society, 1995, 4(5): 667-676. doi: 10.1109/83.382500 [4] WYANT J C. Interferogram analysis: Digital fringe pattern measurement techniques[J]. Optical Engineering, 1993, 32(11): 2987-2988. doi: 10.1117/1.OE.32.11.bookreviews [5] GOLDSTEIN R M, ZEBKER H A, WERNER C L. Satellite radar interferometry: Two-dimensional phase unwrapping[J]. Radio Science, 1988, 23(4): 713-720. doi: 10.1029/RS023i004p00713 [6] XU W, CUMMING I. A region-growing algorithm for InSAR phase unwrapping[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(1): 124-134. doi: 10.1109/36.739143 [7] FLYNN T J. Consistent 2-D phase unwrapping guided by a quality map[C] //1996 International Geoscience and Remote Sensing Symposium. Lincoln, USA: IEEE Press, 1996: 2057-2059. [8] FLYNN T J. Two-dimensional phase unwrapping with minimum weighted discontinuity[J]. Journal of the Optical Society of America, 1997, A14(10): 2692-2701. [9] BONE D J. Fourier fringe analysis: The two-dimensional phase unwrapping problem[J]. Applied Optics, 1991, 30(25): 3627-3632. doi: 10.1364/AO.30.003627 [10] GHIGLIA D C, ROMERO L A. Minimum LP-norm two-dimensional phase unwrapping[J]. Journal of the Optical Society of America, 1996, A13(10): 1999-2013. [11] HYUN J S, ZHANG S. Enhanced two-frequency phase-shifting method[J]. Applied Optics, 2016, 55(16): 4395-4401. doi: 10.1364/AO.55.004395 [12] ZHANG S. Digital multiple wavelength phase shifting algorithm[J]. Proceedings of the SPIE, 2009, 7432: 74320N. doi: 10.1117/12.823903 [13] WANG K Q, LI Y, QIAN K M, et al. One-step robust deep learning phase unwrapping[J]. Optics Express, 2019, 27(10): 15100-15115. doi: 10.1364/OE.27.015100 [14] ZHOU L, YU H, PASCAZIO V, et al. PU-GAN: A one-step 2-D InSAR phase unwrapping based on conditional generative adversarial network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-10. [15] FANG Q, XIA H T, SONG Q H, et al. Speckle denoising based on a deep learning via conditional generative adversarial network in digital holographic interferometry[J]. Optics Express, 2022, 30(12): 20666-20683. doi: 10.1364/OE.459213 [16] SPOORTHI G E, GORTHI S, GORTHI R K S S. PhaseNet: A deep convolutional neural network for two-dimensional phase unwrapping[J]. IEEE Signal Processing Letters, 2018, 26(1): 54-58. [17] SPOORTHI G E, GORTHI R K S S, GORTHI S. PhaseNet 2.0: Phase unwrapping of noisy data based on deep learning approach[J]. IEEE Transactions on Image Processing, 2020, 29: 4862-4872. doi: 10.1109/TIP.2020.2977213 [18] 陈翠茹, 王华英, 赵宝群, 等. 基于UMnet的数字全息相位解包裹[J]. 激光技术, 2023, 47(1): 73-79. doi: 10.7510/jgjs.issn.1001-3806.2023.01.011 CHEN C R, WANG H Y, ZHAO B Q, et al. Digital holographic phase unwrapping based on UMnet[J]. Laser Technology, 2023, 47(1): 73-79(in Chinese). doi: 10.7510/jgjs.issn.1001-3806.2023.01.011 [19] WANG K Q, KEMAO Q, DI J L, et al. Deep learning spatial phase unwrapping: A comparative review[J]. Advanced Photonics Nexus, 2022, 1(1): 014001. [20] SILVIO M, PASCAL P. Quantitative appraisal for noise reduction in digital holographic phase imaging[J]. Optics Express, 2016, 24(13): 14322-14343. doi: 10.1364/OE.24.014322 [21] FAN Ch M, LIU T J, LIU K H. SUNet: Swin transformer UNet for image denoising[C] //2022 IEEE International Symposium on Circuits and Systems (ISCAS). Austin, USA: IEEE, 2022: 2333-2337. [22] LIU Z, HU H, LIN Y, et al. Swin transformer V2: Scaling up capacity and resolution[C]//2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orlean(LA), USA, IEEE Press, 2022: 11999-12009. [23] HE K M, ZHANG X Y, REN S Q, et al. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification[C] //2015 IEEE International Conference on Computer Vision(ICCV). New Yorks, USA: IEEE Press, 2015: 1026-1034. [24] QIAO X F. Information optics digital laboratory: Matlab edition[M]. Beijing: Science Press, 2015: 177-178(in Chinese). -
点击查看大图
图(13) / 表(2)
计量
- 文章访问数: 1381
- HTML全文浏览量: 56
- PDF下载量: 0
- 被引次数: 0
