-
红外成像是将景物辐射或反射的红外光线进行光电转换从而成像,广泛应用于军事、医疗和灾备等领域,但是红外图像往往会存在亮度较暗和对比度较低的不足,降低了红外图像的应用效果[1]。因此,红外图像增强非常必要,以此来改善其亮度和对比度。改善红外图像效果的方法总体上包括直方图映射类方法、基于Retinex颜色恒常性理论的方法和基于学习框架类的增强方法[2]。全局直方图均衡能大大地拉伸图像的对比度,但是对于平滑区域会出现过度增强、而对微小细节区域的增强不足。为了在提升全局对比度的同时,又能改善微小细节的效果,ABHISEK等人[3]提出了一种增强红外图像的方法,其基于平台阈值的直方图均衡化,对平滑区域的直方图进行裁剪,而对微小细节区域的直方图进行补偿。LI等人[4]提出基于自适应阈值裁剪的双平台直方图均衡化,但是平台阈值的确定缺乏鲁棒性,对于不同的图像难以确定最优的平台阈值。为了限制图像的过度增强效果,PAUL等人[5]提出一阵基于自适应限幅的双子直方图均衡算法,但是对图像的亮度和对比度的改善不明显。CHEN等人[6]将高斯差分滤波器与平台直方图结合,更好地提升图像的对比度和显著化边缘信息。YAN等人[7]将红外图像划分为前景和背景两部分,然后分别进行全局直方图均衡增强,虽然对微小细节有一定的增强效果,但是依然无法避免过度增强。SRINIVAS等人[8]采用Hopfield神经网络结构计算能量曲线,将能量曲线分为3个区域,然后分别进行均衡化处理。
Retinex理论认为,图像可分解为低频和高频部分,可根据各自的特征分别进行处理。GU等人[9]根据亮通道先验和Retinex模型将红外图像分解为基础图像和细节图像,用引导滤波和全变分平滑算子去除块效果,保持图像的局部平滑,而根据细节变化先验对细节图像进行锐化。LUO等人[10]将图像分解为多尺度的低频图像和高频图像,而对多尺度的低频图像进行伽马校正,改善图像的亮度和对比度。对图像的低频进行伽马校正能改善图像的亮度,但对图像的细节增强不明显。CHENG等人[11]将图像拆分为入射光部分和反射光部分,用平台直方图均衡增强入射光部分,而对反射图像进行对比度和细节增强,然后将入射光部分与反射光部分融合,但是所采用的多种增强技术以及融合处理,均固定参数不变,缺乏鲁棒性。
近年来,深度学习被广泛应用于红外图像处理中。FAN等人[12]设计一种突出红外图像的前景目标而抑制背景噪声的卷积神经网络,但是通过仿真对训练数据集进行扩充,在一定程度上失去了深度学习的意义。在参考文献[13]中,KUANG等人采用条件生成对抗网络,以进一步优化图像增强效果,但是在可见光图像上进行训练的模型,难以适用于红外图像。PANG等人[14]设计了红外细节增强子网络和全局内容不变子网络,在避免局部过增强的同时,增强图像的深度细节特征和保持图像的空间结构。参考文献[15]中建立了一种用于红外图像增强的渐进融合网络,利用红外光场图像之间丰富的角度视觉来探索和融合红外增强图像的辅助信息。基于深度学习的红外图像增强方法虽然能在一定程度上改善图像的效果,但是受限于红外图像数据集,缺乏鲁棒性,对于不同的图像数据,其效果差异较大[16-18]。
为了克服现有红外图像增强方法的缺陷,在避免过增强的同时,更好地提高红外图像的质量,本文作者提出了融合线性变换与局部均衡的红外图像增强方法。对红外图像分别进行自适应的分段线性变换和局部直方图均衡,然后对两张增强图像进行金字塔分解和对应的加权融合,获得最终的增强图像。实验数据以主、客观的方式证明了所提出的方法优于现有方法。
-
本文中方法的步骤为:先对红外图像分别进行自适应的分段线性变换增强和局部直方图均衡增强,再根据对比度特征、显著性特征和亮度分布特征分别计算两张增强图像的权重图,然后以拉普拉斯金字塔和高斯金字塔的方式,分别对增强图像和权重图进行分解,最后将分解的图像与对应的权重图进行多尺度的线性融合,获得效果理想的红外图像。
-
分段线性变换压缩分布较少的像素所占的灰度级区间,而拉伸分布较多的像素所占的灰度级区间,从而实现像素对灰度级空间的近似均匀分布,一方面改善图像的亮度,另一方面改善图像的对比度。令I(x)为红外图像I中灰度为x的像素,图像的灰度级数为L,灰度级x的动态范围为[0, L-1],像素的分段线性变换方法见下。
(a) 获取图像I的直方图h :
$ \boldsymbol{h}=\{h(x) \mid h(x)=\operatorname{count}(\boldsymbol{I}=x)\} $
(1) 式中:h(x)表示灰度值x对应的直方图中的值;count(I=x)表示统计图像I中灰度级为x的像素数。
(b) 对直方图进行累计求和并进行归一化,H(x)表示灰度级x对应于向量H中的值:
$ \begin{gathered} \boldsymbol{H}=\{H(x) \mid H(0)=h(0), \\ H(x)=H(x-1)+h(x)\} \end{gathered} $
(2) $ \boldsymbol{H}=\frac{\boldsymbol{H}}{H(L-1)} $
(3) (c) 为了保证绝大部分的像素尽可能均匀地分布于灰度级空间,将灰度级的映射目标范围[0, L-1]的5%和95%区间分点分别作为映射范围的上、下分段点:
$ y_1=\operatorname{round}(5 \% \times L)-1 $
(4) $ y_2=\operatorname{round}(95 \% \times L)-1 $
(5) 式中:round(·)为四舍五入取整函数。
(d) 将直方图累计频次为5%和95%对应的灰度级分别作为原图像灰度级的上、下分段点:
$ x_1=\underset{x \in[0, L-1]}{\arg }(H(x) \leqslant 0.05<H(x+1)) $
(6) 或
$ x_1=\underset{x \in[0, L-1]}{\arg }(H(x)<0.05 \leqslant H(x+1))+1 $
(7) $ x_2=\underset{x \in[0, L-1]}{\arg }(H(x) \leqslant 0.95<H(x+1)) $
(8) 或
$ x_2=\underset{x \in[0, L-1]}{\arg }(H(x)<0.95 \leqslant H(x+1))+1 $
(9) 式中:由于存在临界取值,根据H(x)=0.05还是H(x+ 1)=0.05,分段点x1分别有两种定义式;同样的,根据H(x)=0.95还是H(x+1)=0.95,分段点x2也分别有两种定义式。
(e) 分段线性变换。对红外图像I中灰度级为x的像素I(x)分段线性变换,可定义为:
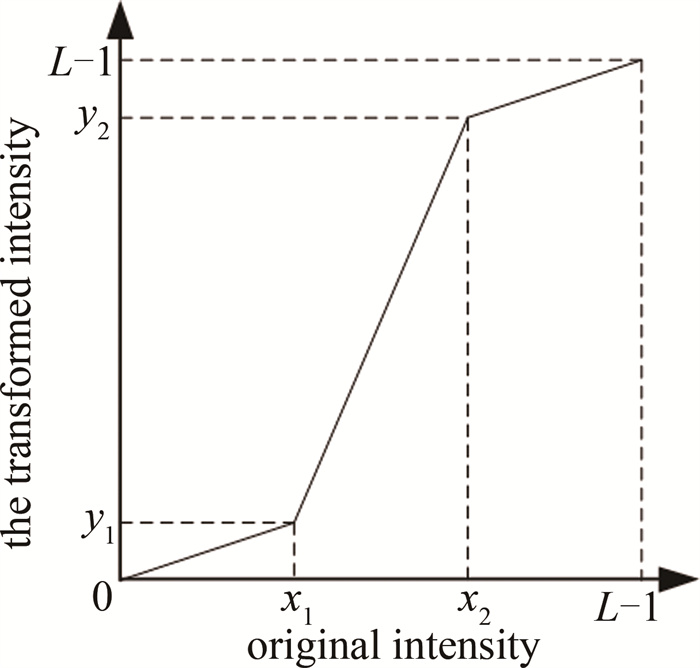
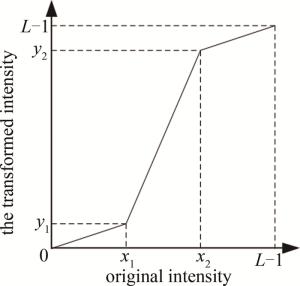
$ I(x)=\left\{\begin{array}{l} \frac{y_1}{x_1} x, \left(x<x_1\right) \\ y_1+\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right), \left(x_1 \leqslant x \leqslant x_2\right) \\ y_2+\frac{(L-1)-y_2}{(L-1)-x_2}\left(x-x_2\right), \left(x_2<x\right) \end{array}\right. $
(10) 分段线性变换的效果如图 1所示。将处于灰度级区间[x1, x2]的近90%的像素,根据灰度级的相对距离,重新分布于较大的灰度级区间[y1, y2],而将处于区间[0, x1]和[x2, L-1]中少数的像素,根据灰度级的相对距离,重新分布于较窄的区间[0, y1]和[y2, L-1]。分段线性变换将图像的像素在整个灰度级动态空间进行近似均匀的重分布,从而改善图像的亮度和对比度。
-
一般地,统一的直方图均衡能明显地拉大图像的对比度,但是会产生过度增强和增强不足。为克服此缺陷,部分学者对直方图均衡方法进行改进,将图像划分为子图像块,分别进行直方图均衡化,但是会产生放大噪声,同时会产生块状效应。于是本文作者提出了局部直方图均衡化方法:对每一像素I(x),令Nx(k)为以I(x)为中心的、大小为k×k的邻域;对邻域Nx(k)中的像素进行直方图均衡化,像素I(x)取对应直方图均衡化后的像素值。方法的具体步骤见下。
(a) 对每一像素I(x),分别统计邻域Nx(k)的最小灰度值m、最大灰度值M和直方图hx:
$ \left\{\begin{array}{l} m=\min \left(N_x(k)\right) \\ M=\max \left(N_x(k)\right) \end{array}\right. $
(11) $ \begin{gathered} h_x(x-m)=\operatorname{count}\left(N_x(k)=x\right) \\ (x=m, \cdots, M) \end{gathered} $
(12) 式中:min(·)和max(·)分别取元素的最小和最大值。
(b) 对直方图hx进行均衡化:
$ \begin{gathered} \boldsymbol{H}_x=\left\{H_x(y) \mid H_x(0)=h_x(0)\right. \\ \left.H_x(y)=H_x(y-1)+h_x(y)\right\} \\ (y=0, \cdots, M-m) \end{gathered} $
(13) (c) 对均衡化后的直方图Hx进行归一化:
$ \boldsymbol{H}_x=\frac{\boldsymbol{H}_x}{H_x(M-m)} $
(14) (d) 对像素I(x)进行灰度映射变换:
$ I(x)=m+H_x(x-m) \times(M-m) $
(15) 步骤(a)中参数k的取值,在一定程度上影响局部对比度的提升:取值过大,微小的边缘细节得不到有效增强;取值过小,整体对比度的提升不明显。本文中通过实验的综合比较,取k=13为最优值。
-
分段线性变换从像素分布上提升了图像的整体对比度,但是对局部的微小细节往往增强不足;而局部直方图均衡化能改善微小细节的对比度,但是对全局对比度的改善尚有欠缺。为了在改善红外图像的全局对比度的同时,局部细节也能得到清晰显示,分别对线性变换的增强图像和局部直方图均衡化增强的图像,根据对比度、显著性和亮度的权重图进行多尺度的金字塔融合,获得最终的增强图像。令线性变换的增强图像和局部直方图均衡化的增强图像分别为Il和Ih。
-
对比度权重矩阵采用拉普拉斯滤波FL的绝对值进行计算。下标t分别是l, h。
$ \boldsymbol{w}_{c, t}=\left|F_{\mathrm{L}}\left(\boldsymbol{I}_t\right)\right| $
(16) 基于对比度权重矩阵的图像融合,可以突出显示对比度较大的像素信息。
显著性权重定义为图像的平均值与高斯平滑滤波FG图像的绝对残差图像:
$ \boldsymbol{w}_{\mathrm{s}, t}=\left|\operatorname{mean}(\boldsymbol{I})-F_{\mathrm{G}}\left(\boldsymbol{I}_t\right)\right| $
(17) 基于显著性权重矩阵的图像融合,可以强调像素的显著性特征。
一般地,效果理想的红外图像的亮度均值为灰度级范围的中值。亮度权重矩阵采用图像与理想亮度的差值的指数函数进行计算:
$ \boldsymbol{w}_{\mathrm{h}, t}=\exp \left[-\frac{\left(\boldsymbol{I}_t-0.5\right)^2}{2 \operatorname{var}\left(\boldsymbol{I}_t\right)}\right] $
(18) 式中:var(·)表示求方差。基于亮度权重的图像融合,通过权重强调亮度适应的像素在结果图像中的作用,而削弱亮度较大或较小的像素的作用,可以有效调节图像的亮度。
增强图像Il和Ih的归一化权重图分别为:
$ \boldsymbol{W}_1=\frac{\sum\limits_{r \in\{\mathrm{c}, \mathrm{~s}, \mathrm{~h}\}} \boldsymbol{w}_{r, \mathrm{l}}}{\sum\limits_{r \in\{\mathrm{c}, \mathrm{~s}, \mathrm{~h}\}} \sum\limits_{t \in\{1, \mathrm{~h}\}} \boldsymbol{w}_{r, t}} $
(19) $ \boldsymbol{W}_{\mathrm{h}}=\frac{\sum\limits_{r \in\{\mathrm{cs, }, \mathrm{~h}\}} \boldsymbol{w}_{r, \mathrm{~h}}}{\sum\limits_{r \in\{\mathrm{c}, \mathrm{~s}, \mathrm{~h}\}} \sum\limits_{t \in\{1, \mathrm{~h}\}} \boldsymbol{w}_{r, t}} $
(20) -
高斯金字塔分解以原图像的高斯滤波图像为第1层,后续迭代地对图像进行下采样和高斯滤波,每一次的下采样和高斯滤波的结果为一层,直到获得指定层次的金字塔图像。
对权重图Wt进行n层的高斯金字塔分解的具体过程为:
$ \boldsymbol{T}_{\boldsymbol{W}, t}(1)=\boldsymbol{W}_t $
(21) $ \boldsymbol{P}_{W, t}(1)=F_{\mathrm{G}}\left(\boldsymbol{T}_{W, t}(1)\right) $
(22) …
$ \boldsymbol{T}_{\boldsymbol{W}, t}(l)=S_{\mathrm{DS}}\left(\boldsymbol{T}_{\boldsymbol{W}, t}(l-1)\right), (2 \leqslant l \leqslant n) $
(23) $ \boldsymbol{P}_{W, t}(l)=F_{\mathrm{G}}\left(\boldsymbol{T}_{W, t}(l)\right), (2 \leqslant l \leqslant n) $
(24) 式中:SDS为下采样;TW,t(l)为下采样金字塔;PW,t(l)为高斯分解的权重图金字塔。
-
$ \boldsymbol{T}_{I, t}(1)=\boldsymbol{I}_t $
(25) $ \boldsymbol{P}_{I, t}(1)=F_{\mathrm{G}}\left(\boldsymbol{T}_{I, t}(1)\right) $
(26) …
$ \boldsymbol{T}_{I, t}(l)=S_{\mathrm{DS}}\left(\boldsymbol{T}_{I, t}(l-1)\right), (2 \leqslant l \leqslant n) $
(27) $ \boldsymbol{P}_{I, t}(l)=F_{\mathrm{G}}\left(\boldsymbol{T}_{I, t}(l)\right), (2 \leqslant l \leqslant n) $
(28) $ \begin{aligned} \boldsymbol{P}_{I, t}(l)= & \boldsymbol{P}_{I, t}(l)-S_{\mathrm{US}}\left(\boldsymbol{P}_{I, l}(l+1)\right), \\ & (1 \leqslant l \leqslant n-1) \end{aligned} $
(29) 式中:SUS为上采样;PI,t(l)为拉普拉斯分解的图像金字塔。
-
$ \boldsymbol{f}(l)=\sum\limits_{t \in\{1, \mathrm{~h}\}} \boldsymbol{P}_{W, t}(l) \times \boldsymbol{P}_{I, t}(l), (1 \leqslant l \leqslant n) $
(30) -
迭代执行:
$ \begin{gathered} \boldsymbol{f}(l-1)=\boldsymbol{f}(l-1)+S_{\mathrm{US}}(\boldsymbol{f}(l)) \\ (l=n, n-1, \cdots, 2) \end{gathered} $
(31) 迭代最后输出的f (1)为金字塔融合的增强图像。
-
实验环境为I7 CPU和32G内存,以相关参考文献[5, 7, 11, 14]中提出的方法作为实验参照。分别根据增强图像的视觉感知效果和增强图像的客观质量指标,以主、客观的方式,证明本文中方法的实用性和优越性。实验素材来源于数据集OTCBVS Benchmark Dataset,其中包含室内和室外的红外图像、近景和远景的红外图像。
-
各方法对5个场景红外图像的增强结果如图 2所示。各方法均能在不同程度上改善红外图像的效果。
参考文献[5]中为限幅的直方图均衡化方法,在保持较亮的前景部分基本不变的情况下,而对较暗的背景部分的对比度有一定程度的改善,但是效果不明显,将直方图分为前景的直方图和背景的直方图,分别进行限幅的直方图均衡化,虽然具有一定的自适应性,且避免了图像的过增强,但是欠增强效果较明显,图像暗区域的增强效果非常有限,图像的整体亮度较暗。参考文献[7]中在方法原理上类似于参考文献[5],将红外图像分为前景部分与背景部分,分别进行直方图均衡化,但是不进行限幅操作;从增强图像上看,参考文献[7]中最明显的特点就是对比度较大,但是因其不进行直方图限幅,在前景部分产生过增强,且部分暗处的图像信息未能得到有效的增强。参考文献[11]中将红外图像分为光照部分和细节部分,分别对其进行平台直方图均衡化和对比度拉伸,基本上避免了图像的过增强,但是增强图像的亮度整体偏低;对部分图像的增强效果较好,比如图 2d2和图 2d3,对于其余图像的对比度增强不足,在部分暗区域产生欠增强,部分图像信息未能正常显示。参考文献[14]中为基于内容和细节深度学习的图像增强方法,从其增强图像可以看出,图像的前景部分会产生失真的效果,比如图 2e1的裤子和图 2e2的车头部分,而背景的对比度较低、雾霾效果比较明显。因为根据可见光图像进行学习训练,导致其难以完全适用于红外图像。
相对地,采用本文中的方法对红外图像增强后,亮度较为适宜,对比度较大,图像暗处的信息得到了有效的增强,前景和背景的场景信息均得到较明显的增强。本文中的方法将自适应的分段线性变换和局部直方图均衡化的增强结果进行了多尺度的金字塔融合,除了图 2f2的车头部分和图 2f5的右下角产生少部分过增强效果之外,本文中方法的增强性能相对于现有方法有一定的优势。
-
本文中采用信息熵[19]、平均梯度[20]和变异系数(coefficient of variation, CV)[21]作为增强图像的质量指标,对增强图像进行评价。信息熵度量图像的有效信息量越大,图像的信息含量越大;平均梯度度量图像的对比度越大,图像的对比度越大;变异系数反映像素的离散程度,值越大,图像的边缘细节越清晰。
对应于图 2,采用各方法对5个场景红外图像进行增强后的信息熵、平均梯度和变异系数分别如表 1~ 表 3所示。
表 1 增强图像的信息熵
Table 1. Entropy of enhanced images
表 2 增强图像的平均梯度
Table 2. Average gradient of enhanced image
表 3 增强图像的变异系数
Table 3. Coefficient of variation of enhanced images
根据表 1中增强图像的信息熵可以看出,参考文献[5]中对原图像的信息熵的提升不明显,未能明显增加图像的有效信息含量;参考文献[7]中对各图像增强后的信息熵较大,明显提升图像的信息含量;而参考文献[11]和参考文献[14]中信息熵次之,两者的信息熵相差不大,但次于参考文献[7]和本文中方法。相对地,本文中方法的信息熵最大,能更有效地增加图像的有效信息含量。
采用各方法对不同场景的红外图像进行增强处理后,所获得的平均梯度如表 2所示。很明显,参考文献[5]和参考文献[14]中的平均梯度较小,对图像对比度的改善不明显;而参考文献[11]中的平均梯度比参考文献[5]和参考文献[14]要大,但是相对原图像的平均梯度,提升的幅度依然不明显;参考文献[7]中和本文中的方法平均梯度较大,能明显地提升图像的对比度,但是参考文献[7]在前景部分会产生过增强,破坏部分图像信息,因此其平均梯度小于本文中方法。
采用各方法对红外图像增强后的变异系数如表 3所示。由比较可知,参考文献[14]中的变异系数较小,增强图像的边缘细节信息较模糊;参考文献[5]中的变异系数相对于原图像提升的幅度也不明显,所以难以有效地显示边缘和细节信息;参考文献[7]和参考文献[11]中的变异系数较大,两者相差不大,能在较大程度上改善图像的边缘细节的清晰度。相对地,本文中方法获得的变异系数更大,能更有效地提升图像的边缘细节的清晰度。
以上增强图像的视觉感知效果以及增强图像的信息熵、平均梯度和变异系数,均证明了本文中的方法能更理想地提升红外图像的质量,更能显著化红外图像的边缘和细节。
-
为了更有效地改善红外图像的效果,提出了融合线性变换和局部均衡的方法。对红外图像分别进行自适应的分段线性变换和局部直方图均衡,然后对增强图像进行多尺度的金字塔融合。实验数据显示,本文中的方法能规避图像的过度增强,而且能较理想地改善图像的亮度、对比度和边缘细节的清晰度,具有更好的红外图像增强效果。改善提出方法的计算逻辑、降低方法的计算复杂度,是课题组下一步的研究方向。
线性变换与局部均衡融合的红外图像增强
Infrared image enhancement by fusion of lineartransformation and local equalization
-
摘要: 为了改善红外图像的效果,提升对比度和清晰度,丰富边缘细节信息,提出了融合线性变换和局部均衡的红外图像增强方法。利用图像的像素值分布,对像素值进行自适应的分段线性变换,并用局部的直方图均衡增强图像;分别计算两张增强图像的权重图。对比度权重、显著性权重和亮度分布权重;以拉普拉斯金字塔和高斯金字塔的方式,分别对增强图像和权重图进行分解,将分解的图像与权重图进行多尺度线性融合,获得效果理想的增强图像。结果表明,相对于现有方法,本文中提出的方法增强图像的视觉效果更清晰,信息熵、平均梯度和变异系数分别比现有方法高出9.03%、23.87%和9.97%以上。该研究可更有效地提高红外图像增强的性能。Abstract: Aiming at improving the effect of infrared image, increasing its contrast and clarity and enriching its edge and detail information, an infrared image enhancement method by fusion of linear transformation and local equalization was proposed. According to the intensity distribution of image, adaptive piecewise linear transformation on the intensity of pixel was performed, and local histogram equalization on the image was carried out. Then, the contrast weight, saliency weight and brightness weight of the two enhanced images were calculated, respectively. Finally, multi-scale Laplace pyramid decomposition and Gaussian pyramid decomposition were performed on the enhanced images and the corresponding weights, respectively, and multi-scale linear fusion with the decomposed images and the corresponding weights were performed to obtain the final enhanced image. According to the experimental results, it is confirmed that the effectiveness of proposed method compared to existing methods, the enhanced images go with better visual effect, and the information entropy, average gradient and coefficient of variation are higher than existing methods by more than 9.03%, 23.87% and 9.97%, respectively. This study could improve infrared image enhancement performance more effectively.
-
表 1 增强图像的信息熵
Table 1. Entropy of enhanced images
表 2 增强图像的平均梯度
Table 2. Average gradient of enhanced image
表 3 增强图像的变异系数
Table 3. Coefficient of variation of enhanced images
-
[1] 陶昕辰, 朱涛, 黄玉玲, 等. 基于DDR GAN的低质量图像增强算法[J]. 激光技术, 2023, 47(3): 322-328. TAO X Ch, ZHU T, HUANG Y L, et al. Low-quality image enhancement algorithm based on DDR GAN[J]. Laser Technology, 2023, 47(3): 322-328 (in Chinese). [2] 顾振飞, 陈灿, 陈勇, 等. 基于透射先验的弱光照图像增强方法[J]. 传感技术学报, 2021, 34(10): 1300-1306. GU Zh F, CHEN C, CHEN Y, et al. Transmission prior-based enhancement method for low-lightimage[J]. Chinese Journal of Sensors and Actuators, 2021, 34(10): 1300-1306 (in Chinese). [3] ABHISEK P, PRANTIK B, PARITOSH B, et al. Power-log based plateau limit histogram equalization algorithm for infrared image enhancement[C]// 2017 Tenth International Conference on Contemporary Computing (Ic3). New York, USA: IEEE Press, 2017: 38-42. [4] LI S, JIN W, LI L, et al. An improved contrast enhancement algorithm for infrared images based on adaptive double plateaus histogramequalization[J]. Infrared Physics & Technology, 2018, 90: 164-174. [5] PAUL A, SUTRADHAR T, BHATTACHARYA P, et al. Adaptive clip-limit-based bi-histogram equalization algorithm for infrared image enhancement[J]. Applied Optics, 2020, 59(28): 9032-9041. doi: 10.1364/AO.395848 [6] CHEN Y, ZHANG H, ZHAO Z, et al. Ultra-fast detail enhancement for a short-wave infraredimage[J]. Applied Optics, 2022, 61(17): 5112-5120. doi: 10.1364/AO.455947 [7] 闫哲, 蒋砾, 杨帆, 等. 基于双直方图均衡算法的红外图像增强[J]. 红外技术, 2022, 44(9): 944-950. YAN Zh, JIANG L, YANG F, et al. Bi-histogram equalization algorithm for infrared imageenhancement[J]. Infrared Technology, 2022, 44(9): 944-950(in Chinese). [8] SRINIVAS K, BHANDARI A K, KUMAR P K, et al. A context-based image contrast enhancement using energy equalization with clippinglimit[J]. IEEE Transactions on Image Processing, 2021, 30: 5391-5401. doi: 10.1109/TIP.2021.3083448 [9] GU Z, JU M, ZHANG D. A novelretinex image enhancement approach via brightness channel prior and change of detail prior[J]. Pattern Recognition and Image Analysis, 2017, 27(2): 234-242. doi: 10.1134/S1054661817020055 [10] 罗国强, 陈家益. 改进双边滤波与平均γ矫正的图像增强[J]. 传感技术学报, 2022, 35(5): 644-649. LUO G Q, CHEN J Y. Image enhancement based on improved bila-teral filtering and averageγcorrection[J]. Chinese Journal of Sensors and Actuators, 2022, 35(5): 644-649(in Chinese). [11] 程铁栋, 卢晓亮, 易其文, 等. 一种结合单尺度Retinex与引导滤波的红外图像增强方法[J]. 红外技术, 2021, 43(11): 1081-1088. CHENG T D, LU X L, YI Q W, et al. Research on infrared image enhancement method combined with single-scale Retinex and guided imagefilter[J]. Infrared Technology, 2021, 43(11): 1081-1088(in Chinese). [12] FAN Z, BI D, XIONG L, et al. Dim infrared image enhancement based on convolutional neuralnetwork[J]. Neurocomputing, 2018, 272: 396-404. doi: 10.1016/j.neucom.2017.07.017 [13] KUANG X, SUI X, LIU Y, et al. Single infrared image enhancement using a deep convolutional neuralnetwork[J]. Neurocomputing, 2019, 332: 119-128. doi: 10.1016/j.neucom.2018.11.081 [14] PANG Z X, LIU G H, LI G S, et al. An infrared image enhancement method via content and detail two-stream deep convolutional neuralnetwork[J]. Infrared Physics & Technology, 2023, 132: 104761. [15] MA Y, WANG X, GAO W, et al. Progressive fusion network based on infrared light field equipment for infrared image enhancement[J]. IEEE/CAA Journal of Automatica Sinica, 2022, 9(9): 1687-1690. doi: 10.1109/JAS.2022.105812 [16] MA J, GAO W, MA Y, et al. Learning spatial-parallax prior based on array thermal camera for infrared imageenhancement[J]. IEEE Transactions on Industrial Informatics, 2022, 18(10): 6642-6651. [17] 刘翠连, 陶于祥, 罗小波, 等. 混合卷积神经网络的高光谱图像分类方法[J]. 激光技术, 2022, 46(3): 355-361. LIU C L, TAO Y X, LUO X B, et al. Hyperspectral image classification based on hybrid convolutional neural network[J]. Laser Technology, 2022, 46(3): 355-361(in Chinese). [18] 刘光晖, 杨琦, 孟月波, 等. 一种并行混合注意力的渐进融合图像增强方法[J]. 光电工程, 2023, 50(4): 220231. LIU G H, YANG Q, MENG Y B, et al. A progressive fusion image enhancement method with parallel hybrid attention[J]. Opto-Electronic Engineering, 2023, 50(4): 220231(in Chinese). [19] 郑伟, 李涵, 安晓林, 等. 基于ShearLab 3D变换的3维PET/MRI图像融合[J]. 激光技术, 2021, 45(1): 86-92. ZHENG W, LI H, AN X L, et al. 3-D PET/MRI image fusion based on ShearLab 3D transform[J]. Laser Technology, 2021, 45(1): 86-92(in Chinese). [20] ASHIBA M, TOLBA M, EL-FISHAWY A, et al. Hybrid enhancement of infrared night vision imagingsystem[J]. Multimedia Tools & Applications, 2020, 79(9/10): 6085-6108. [21] LI S, JIN W, WANG X, et al. Contrast enhancement algorithm for outdoor infrared images based on local gradient-grayscale statisticalfeature[J]. IEEE Access, 2018, 6: 57341-57352. -


 网站地图
网站地图

 下载:
下载: