-
高光谱图像丰富的光谱特征可以促进成像场景的表征,已被证明可极大提高目标检测[1]、环境监测[2]和图像分类[3]等任务的性能,在遥感应用中具有重要意义。然而,成像过程中存在许多因素,如噪声和低感知分辨率,都会导致采集过程中图像退化。在进一步处理之前,通常采用退化高光谱图像和退化多光谱图像的融合框架来重建高空间分辨率的高光谱图像。现有的高光谱超分辨率方法大致分为3类:基于矩阵分解的方法、基于张量分解的方法和基于深度学习的方法。
基于矩阵分解的方法中具有代表性的是耦合非负矩阵分解(coupled non-negative matrix factorization,CNMF)[4]。CNMF是一个典型的不适定逆问题,需要引入先验信息或添加正则项来缩小优化问题的解空间。YANG等人[5]在CNMF中引入近似最小体积单纯形正则和稀疏正则,并通过近似交替优化降低了模型的复杂度。AHMAD等人[6]扩展了线性混合模型,考虑解混模型中的非线性效应以增强高光谱图像的空间分辨率。然而,矩阵分解将3维高光谱数据展开成矩阵,会导致观测到的高光谱图像和多光谱图像的结构信息丢失,使重建图像的空间和光谱畸变程度增加。
基于张量分解的方法能够在不破坏原始数据结构的同时有效地重建高分辨率图像。常见的张量分解形式包括典范多因子(canonical polyadic,CP)[7]分解和Tucker分解[8]。KANATSOULIS等人[7]提出了一种基于CP分解的耦合张量分解模型,在空间和光谱下采样算子未知的情况下融合了高光谱图像和多光谱图像。MA等人[8]对Tucker分解的因子矩阵与核张量分别施加图平滑和低秩正则来重构高分辨图像。尽管张量分解的方法有效保存了高光谱图像的空间结构,但张量分解的物理意义并不明确,可能会导致算法的应用场景受限,而且这类算法的运算复杂度较高。
近年来,深度学习在高光谱数据处理中倍受关注,深度网络模型可以自适应地提取高光谱和多光谱图像之间的互补信息,进而重构同时具有高空间和高光谱分辨率的图像。卷积神经网络(convolutional neural network,CNN)[9]和生成式对抗网络(generative adversarial network,GAN)[10]是两种常用的模型。深度卷积网络可以提取图像的局部特征,并通过多层堆叠捕获全局特征。HU等人[9]将注意力机制整合到CNN中,提出了一种基于空间-光谱卷积的高光谱和多光谱图像融合算法。GAN通过联合训练生成器和判别器生成高分辨率的高光谱图像。XIAO等人[10]将空间和光谱退化模型引入GAN,通过光谱和空间的差异信息估计图像退化算子来融合高光谱和多光谱图像。然而,GAN模型在训练中存在动态平衡问题,且对超参数设置敏感。随着transformer模型的出现,利用注意力机制可以直接提取图像的全局特征。HU等人[11]将transformer模型应用于提取高光谱图像中不同全局特征之间的内在关系,并利用空间残差降低了网络的复杂度。
基于深度学习的方法虽然获得了强劲的性能,但忽略了退化模型中的模糊和降采样算子以及光谱响应函数。为了解决这一问题,结合物理优化模型和深度学习,本文作者提出了一种基于深度神经网络特征提取的高光谱超分辨率算法(hyperspectral super-resolution algorithm based on deep neural network feature extraction,DHSR)。首先,分别设计基于卷积神经网络的空间融合模块和光谱融合模块,用于提取观测图像的空间和光谱特征;然后,构建基于swin-transformer模型的深度特征融合模块(deep feature fusion module,DFFM),融合上一阶段提取到的特征信息;最后,将DFFM的输出反馈到物理优化模型,利用交替方向乘子法(alternating direction method of multipliers,ADMM)进行低复杂度求解得到最终的目标图像。仿真实验结果表明,本文中提出的模型可以在有效保持重构图像空间-光谱特征的同时抑制噪声的干扰。
-
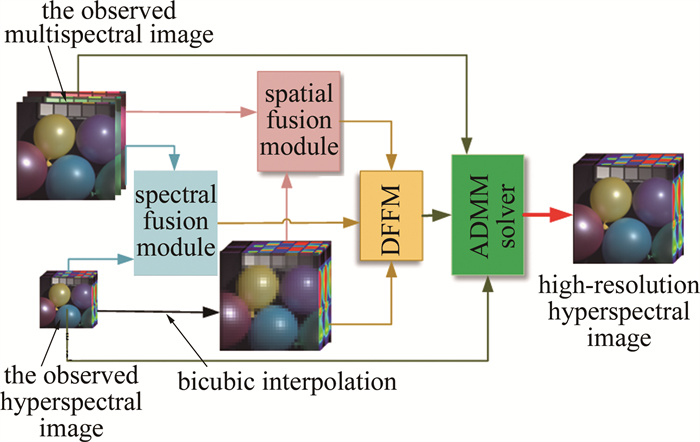
图 1是本文作者提出的DHSR算法的流程图。通过融合观测高光谱图像$ \boldsymbol{Y} \in \mathbf{R}^{n_{\mathrm{w}} \times n_{\mathrm{h}} \times N_{\mathrm{a}}}$和多光谱图像$ \boldsymbol{X} \in \mathbf{R}^{N_{\mathrm{w}} \times N_{\mathrm{h}} \times n_{\mathrm{a}}}$,最终重建高空间分辨率的高光谱图像$ \boldsymbol{Z} \in \mathbf{R}^{N_{\mathrm{w}} \times N_{\mathrm{h}} \times N_{\mathrm{a}}}$。观测高光谱和观测多光谱可以看作是目标图像分别在空间和光谱维度进行下采样得到的。R是实数域,表示高光谱的维度是实数;N表示参考的维度;n表示退化后的维度;下标w,h,a分别表示高光谱图像的宽、高(这是空间维度)和光谱维度。
图 1 基于自适应特征提取的高光谱图像超分辨率方法的流程图
Figure 1. Flowchart of hyperspectral image super-resolution method based on adaptive feature extraction
高光谱图像和多光谱图像的退化模型可以表示为:
$ \boldsymbol{Y}_{(3)}=\boldsymbol{Z}_{(3)} \boldsymbol{B}+E_y $
(1) $ \boldsymbol{X}_{(3)}=\boldsymbol{R} \boldsymbol{Z}_{(3)}+E_x $
(2) 式中:$ \boldsymbol{Z}_{(3)} \in \mathbf{R}^{N_{\mathrm{a}} \times N_{\mathrm{w}} \times N_{\mathrm{h}}}$,表示将3-D的目标图像 Z沿着光谱维度(以模-3的形式)展开得到;$ \boldsymbol{X}_{(3)} \in \mathbf{R}^{N_{\mathrm{a}} \times N_{\mathrm{w}} \times N_{\mathrm{h}}}$和$ \boldsymbol{Y}_{(3)} \in \mathbf{R}^{N_{\mathrm{a}} \times n_{\mathrm{w}} \times n_{\mathrm{h}}}$分别是多光谱图像和高光谱图像按模-3展开的矩阵形式;下标(3)表示模-3,是沿高光谱立方体的光谱维度;$ \boldsymbol{B} \in \mathbf{R}^{N_{\mathrm{w}} \times N_{\mathrm{h}} \times n_{\mathrm{w}} \times n_{\mathrm{h}}} \text { 和 } \boldsymbol{R} \in \mathbf{R}^{n_{\mathrm{a}} \times N_{\mathrm{a}}}$分别表示空间下采样矩阵和光谱下采样矩阵,通常可以通过传感器参数获取;Ey和Ex为误差项。
根据最优化理论,融合问题可以表示为:
$ \min _{\boldsymbol{Z}_{(3)}} \frac{1}{2}\left\|\boldsymbol{Y}_{(3)}-\boldsymbol{Z}_{(3)} \boldsymbol{B}\right\|_{\mathrm{F}}{ }^2+\frac{1}{2}\left\|\boldsymbol{X}_{(3)}-\boldsymbol{R} \boldsymbol{Z}_{(3)}\right\|_{\mathrm{F}}{ }^2 $
(3) 式中:下标F表示Frobenius范数。式(3)是一个不适定的逆问题,为了限制解空间,在此基础上引入了对目标图像Z(3)的自适应先验正则化,使重建图像能保留观测图像在空间和光谱上的先验特征。因此,最终的融合问题可以表示为:
$ \begin{gathered} \min _{\mathbf{Z}_{(3)}} \frac{1}{2}\left\|\boldsymbol{Y}_{(3)}-\boldsymbol{Z}_{(3)} \boldsymbol{B}\right\|_{\mathrm{F}}^2+ \\ \frac{1}{2}\left\|\boldsymbol{X}_{(3)}-\boldsymbol{R} \boldsymbol{Z}_{(3)}\right\|_{\mathrm{F}}^2+\alpha \phi\left(\boldsymbol{Z}_{(3)}\right) \end{gathered} $
(4) 式中:$ \phi(\cdot)$表示由深度网络自适应提取的深度先验正则项;α表示深度先验正则化参数。通过参数α可以平衡重建结果和神经网络所提取特征的吻合性。当α趋向于无穷大时,表示重建图像和深度神经网络提取到先验特征完全一致。
式(4)的正则项中,图像重建结果与网络提取到的深度先验信息有很强的相关性,如果网络能够提取到足够的先验信息,那么在选取合理的正则化参数之后可以显著提升图像的重建精度。对于先验特征的估计,设计了基于CNN的光谱融合模块和空间融合模块以及基于swin-transformer模型的DFFM特征融合模块来提取图像的全局先验,联合使用CNN和transformer模型可以同时提取到图像中的低频信息和高频信息[12]。
-
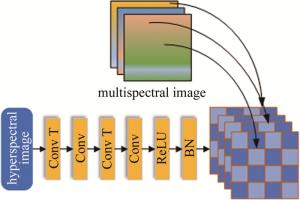
通常情况下认为高光谱图像包含丰富的光谱信息,而多光谱图像包含大量的空间信息,但实际上多光谱图像中仍然包含一定量的光谱信息,只是它所包含的光谱信息明显少于高光谱图像。为了充分利用这两种图像中的光谱信息,设计了一个光谱融合模块,如图 2所示。图中,BN(batch normailization)层是批量样本归一化层;Conv(convolution)是卷积层;Conv T是转置卷积层(反卷积层);ReLU(rectification linear unit)是修正线性单元,是激活函数层。
在此模块中,首先通过转置卷积将低空间分辨率的高光谱图像进行空间上采样,使其空间尺寸与多光谱图像相同;接着将上采样后的高光谱图像与多光谱图像在光谱维度上进行拼接。值得说明的是,图像拼接并不是直接对两张图像在光谱维度上进行堆叠,而是将多光谱图像均匀地插入通过转置卷积后的高光谱图像中。这种拼接方法使得高光谱图像和多光谱图像的光谱覆盖范围重叠,可以进一步降低融合图像的光谱畸变。
光谱融合模块的输出的特征图I可以表示为:
$ \boldsymbol{I}=F_1\left(\boldsymbol{Y}, \boldsymbol{X} ; \theta_1\right) $
(5) 式中:$ F_1(\cdot)$表示光谱融合模块;θ1表示光谱模块中的待学习参数。
-
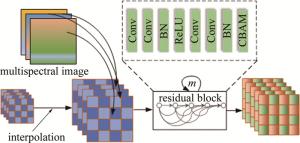
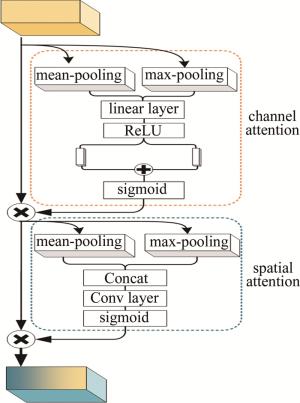
图 3是空间特征融合模块的结构图。首先使用双立方插值对高光谱图像Y进行空间插值,使其空间尺寸和多光谱图像相等;然后采取与光谱融合模块类似的操作,将多光谱图像均匀地插入到插值后的高光谱图像中,完成光谱维度的拼接;最后将拼接后的张量送入基于残差连接的网络中。残差网络由m个结构相同的残差块构成,每个残差块中主要包含卷积层和激活层,并在其输出端添加了卷积块注意力模块(convolutional block attention module,CBAM)[13]。CBAM包括通道注意力和空间注意力两部分,结构如图 4所示。图中,Concat(concatenate)是连接层。
通过计算输入特征图中每个通道和每个位置的重要性并分别加权,从而使得神经网络聚焦于重要的特征,忽略背景等其它次要特征。在高光谱图像中,应用通道注意力可以使网络更加关注主要的光谱特征,从而降低光谱畸变;应用空间注意力可以使网络更加关注前景特征而忽略背景信息。最终,空间融合模块提取到的特征图I2可以用下式表示:
$ \boldsymbol{I}_2=F_2\left(\hat{\boldsymbol{Y}}, \boldsymbol{X} ; \theta_2\right) $
(6) 式中:$ \hat{\boldsymbol{Y}}$表示插值后的高光谱图像;F2(·)表示空间融合模块;θ2表示空间融合模块中的待学习参数。
-
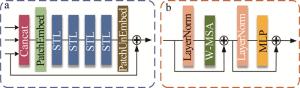
特征融合模块的核心目标是将光谱融合模块、空间融合模块以及插值后的高光谱图像进一步整合,以便最终提取高光谱图像的全局先验特征。如图 5a所示,特征融合模块首先将光谱融合模块、空间融合模块的输出结果以及插值后的高光谱图像在光谱维度进行拼接,得到初始特征图。接着,将特征图输入PatchEmbed模块提取图像的局部嵌入表示。在获得嵌入表示后,利用swin-transformer层(swin-transformer layer,STL)自适应地交互光谱融合模块和空间融合模块提取到的光谱特征和空间特征,从而捕获输入数据的全局特征[14-15]。swin-transformer将滑动窗口机制引入transformer中,从而显著降低了transformer在图像处理中的计算量。本文作者对swin-transformer进行了改进,去除了其中的patch merging模块,使网络不再具备金字塔结构,从而在前向传播过程中保持空间尺寸不变。图中,MLP(multi-layer perceptron)表示多层感知机;W-MSA(window-based multi-head self-attention)表示窗口自注意力机制;LayerNorm表示层归一化。STL的主体结构如图 5b所示。在特征融合模块最后添加了PatchUnEmbed模块,将嵌入后的图像数据还原为图像形式[16]。
通过计算估计值和真实值之差的绝对值,可以得到网络的整体损失函数为:
$ \begin{gathered} l\left(\theta_1, \theta_2, \theta_3\right)= \\ \sum\limits_{i=1}^N\left\|F_3\left(F_1\left(\boldsymbol{Y}_i, \boldsymbol{X}_i ; \theta_1\right), F_2\left(\hat{\boldsymbol{Y}}_i, \boldsymbol{X}_i ; \theta_2\right), \hat{\boldsymbol{Y}}_i ; \theta_3\right)-\hat{\boldsymbol{Z}}_i\right\|_1= \\ \sum\limits_{i=1}^N\left\|F_3\left(\boldsymbol{I}_1, \boldsymbol{I}_2, \hat{\boldsymbol{Y}}_i ; \theta_3\right)-\hat{\boldsymbol{Z}}_i\right\|_1 \end{gathered} $
(7) 式中:F3表示F1和F2进一步整合以提取高光谱图像的全局先验;θ3是特征模块中的待学习参数;$ \left\{\boldsymbol{Y}_i, \hat{\boldsymbol{Y}}_i, \left.X_i ; \hat{\boldsymbol{Z}}_i\right\}_{i=1}^N\right.$表示第i组训练图像对;上标^表示插值。
$ \tilde{\boldsymbol{Z}}=F_3(\boldsymbol{Y}, \tilde{\boldsymbol{Y}}, \boldsymbol{X}) $
(8) 根据网络输出的特征图$ \tilde{\boldsymbol{Z}}$可以得到对目标图像的先验正则项表达式:
$ \phi\left(\boldsymbol{Z}_{(3)}\right)=\frac{1}{2}\left\|\boldsymbol{Z}_{(3)}-\tilde{\boldsymbol{Z}}_{(3)}\right\|_{\mathrm{F}}^2 $
(9) 式中:$ \tilde{\boldsymbol{Z}}_{(3)}$表示对网络输出的特征图$ \tilde{\boldsymbol{Z}}$进行模-3展开得到的矩阵形式;上标~表示重建。
特征融合模块不仅注入了退化多光谱图像中的空间信息和退化高光谱图像中光谱信息,同时也注入了对应的谱域信息和空域信息,防止了关键信息的丢失。引入swin-transformer不仅自适应提取到了空间和光谱特征互补的全局特征,而且减少了信息冗余,降低了计算复杂度。
-
将深度神经网络提取到的自适应先验信息式(9)整合到式(4)中,再引入变量分离可以得到:
$ \begin{gathered} \min _{Z_{(3)}, \boldsymbol{W}} \frac{1}{2}\left\|\boldsymbol{Y}_{(3)}-\boldsymbol{Z}_{(3)} \boldsymbol{B}\right\|_{\mathrm{F}}^2+ \\ \frac{1}{2}\left\|\boldsymbol{X}_{(3)}-\boldsymbol{R} \boldsymbol{W}\right\|_{\mathrm{F}}{ }^2+\frac{\alpha}{2}\left\|\boldsymbol{Z}_{(3)}-\tilde{\boldsymbol{Z}}_{(3)}\right\|_{\mathrm{F}}^2 \end{gathered} $
(10) 式中:W=Z(3)。根据式(10)可以直接得到对应的增广拉格朗日函数:
$ \begin{gathered} L\left(\boldsymbol{Z}_{(3)}, \boldsymbol{W}\right)=\frac{1}{2}\left\|\boldsymbol{Y}_{(3)}-\boldsymbol{Z}_{(3)} \boldsymbol{B}\right\|_{\mathrm{F}}^2+ \\ \frac{1}{2}\left\|\boldsymbol{X}_{(3)}-\boldsymbol{R} \boldsymbol{W}\right\|_{\mathrm{F}}^2+\frac{\alpha}{2}\left\|\boldsymbol{Z}_{(3)}-\tilde{\boldsymbol{Z}}_{(3)}\right\|_{\mathrm{F}}^2+ \\ \frac{\eta}{2}\left\|\boldsymbol{Z}_{(3)}-\boldsymbol{W}+\frac{\Lambda}{\eta}\right\|_{\mathrm{F}}^2 \end{gathered} $
(11) 式中:Λ是拉格朗日乘子;η是增广拉格朗日系数。对式(11)利用ADMM可以求得各变量交替更新的解析表达式:
$ \begin{gathered} \boldsymbol{Z}_{(3)}^{(k+1)}=\left(\boldsymbol{Y}_{(3)} \boldsymbol{B}^{\mathrm{T}}+\alpha \tilde{\boldsymbol{Z}}_{(3)}-\eta \boldsymbol{W}^{(k)}+\right. \\ \left.\Lambda^{(k)}\right)\left(\boldsymbol{B} \boldsymbol{B}^{\mathrm{T}}+\alpha \boldsymbol{I}+\eta \boldsymbol{I}\right)^{-1} \end{gathered} $
(12) $ \begin{gathered} \boldsymbol{W}^{(k+1)}= \\ \left(\boldsymbol{R}^{\mathrm{T}} \boldsymbol{R}+\eta \boldsymbol{I}\right)^{-1}\left(\boldsymbol{R}^{\mathrm{T}} \boldsymbol{X}_{(3)}+\eta \boldsymbol{Z}_{(3)}^{(k+1)}-\Lambda^{(k)}\right) \end{gathered} $
(13) $ \Lambda^{(k+1)}=\Lambda^{(k)}+\eta\left(\boldsymbol{W}^{(k+1)}-\boldsymbol{Z}_{(3)}{ }^{(k+1)}\right) $
(14) 式中:I是单位矩阵。通过对各变量进行交替迭代可以得到最终的重构图像。
综上所述,本文作者提出的DHSR算法可以按以下步骤进行求解:(a)通过深度CNN提取高光谱图像和多光谱图像的深度先验信息$ \tilde{\boldsymbol{Z}}_{(3)}$,输入:$ \boldsymbol{Y}_{(3)} \in \mathbf{R}^{N_{\mathrm{a}} \times n_{\mathrm{w}} n_{\mathrm{h}}}, \boldsymbol{X}_{(3)} \in \mathbf{R}^{n_{\mathrm{a}} \times N_{\mathrm{w}} N_{\mathrm{h}}}, \boldsymbol{B} \in \mathbf{R}^{n_{\mathrm{w}} n_{\mathrm{h}} \times N_{\mathrm{w}} N_{\mathrm{h}}}, \boldsymbol{R} \in \mathbf{R}^{n_{\mathrm{a}} \times N_{\mathrm{a}}}$; 输出:$ \boldsymbol{Z}_{(3)}^{(k+1)} \in \mathbf{R}^{N_{\mathrm{a}} \times N_{\mathrm{w}} N_{\mathrm{h}}}$;(b)将待估计的目标图像$ \tilde{\boldsymbol{Z}}_{(3)}$初始化为$ \tilde{\boldsymbol{Z}}_{(3)}: \boldsymbol{Z}_{(3)}=\tilde{\boldsymbol{Z}}_{(3)}$, k=0,k值最大为30;将高光谱图像Y以及多光谱图像X输入深度神经网络提取深度先验特征$ \tilde{\boldsymbol{Z}}_{(3)}$;(c)对式(12)~式(14)进行循环迭代,当k < 30时,通过式(12)更新Z(3),通过式(13)更新W,通过式(14)更新Λ, k=k+1。实验中设置当相邻两次迭代之间的相对误差小于10-3时,算法收敛,即:
$ \left|\frac{f\left(\boldsymbol{Z}_{(3)}{ }^{(k+1)}-f\left(\boldsymbol{Z}_{(3)}{ }^{(k)}\right.\right.}{f\left(\boldsymbol{Z}_{(3)}{ }^{(k)}\right)}\right| \leqslant 10^{-3} $
(15) 式中:$ f\left(\boldsymbol{Z}_{(3)}{ }^{(k)}\right)$表示优化的目标函数。
-
为了验证本文中提出的DHSR算法的有效性,下面将从多个角度对其进行性能评估。首先,依照Wald协议流程,根据退化模型,利用空间下采样矩阵对参考图像在空间维度下采样得到观测高光谱,利用光谱下采样矩阵得到观测多光谱。实验中采用多个评价指标来定量评估DHSR算法的重建性能,包括重建信噪比(reconstruction signal-to-noise ratio,RSNR)[17]、均方根误差(root mean squared error,RMSE)[18]、相对无量纲全局误差(erreur relative globale adimensionnelle de synthèse,ERGAS)[19]、光谱角制图(spectral angle mapper,SAM)[20]和结构相似度(structural similarity index measure,SSIM)[21]。
-
为了客观评估算法的实际性能,采用两组不同传感器采集的数据集进行了仿真实验。一组数据是CAVE数据集[22],该数据集是由冷却电荷耦合器件(charge-coupled device, CCD)相机拍摄的一系列室内高光谱图像。原始的CAVE数据集中包含32张512×512个空间像素大小的图像,每张图像包括31个波段,覆盖400 nm~700 nm的光谱范围。另一组数据集是Harvard数据集[23],它是由商用高光谱相机拍摄的一系列自然高光谱场景,其中包括室内和室外图像。该数据集中的每个图像包含1040×1392个空间像素和31个光谱波段,覆盖了420 nm~720 nm的光谱范围。尺寸过大的图像会导致运算量大幅增加,为了减少计算量,选择每张图片中512×512个空间像素的区域进行性能测试实验。
本文中提出的DHSR算法需要预训练一个深度特征提取网络,在实验中分别随机选取这两个数据集中的80%作为训练集对网络进行训练,然后测试另外20%的平均性能作为最终的测试结果。在高光谱图像和多光谱图像的获取中不可避免地会受到噪声的干扰,为了评估算法的抗噪声性能,仿真实验分别设置高光谱图像和多光谱图像的信噪比均为30 dB和35 dB来测试算法的抗噪性能。
-
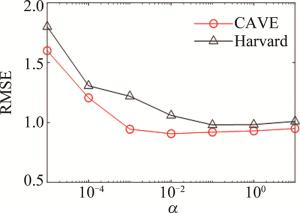
本文中提出DHSR算法中的参数α用于平衡正则项和数据拟合项之间的权重,实验中根据RMSE最小准则来设置该参数的具体取值,算法的RMSE性能随参数变化的趋势如图 6所示。从图中可以看出,α的取值对算法性能有较大影响,最终考虑图像的噪声水平以及算法的稳定性,将α设置为0.1。
-
为了全面评估本文作者提出的DHSR算法在不同数据集上的性能,选择5种代表性的融合方法作为基准,其中包括基于矩阵分解的CNMF[3]和贝叶斯稀疏表示(Bayesian sparse representation,BSR)[24]、基于张量分解的耦合稀疏张量分解(coupled sparse tensor factorization,CSTF)[25]、非局部稀疏张量分解(non-local sparse tensor factorization, NLSTF)[26]和超分辨率张量重构(super-resolution tensor-reconstruction, SRTR)[7]。首先在两种噪声条件下测试了提出的DHSR算法和基准算法在CAVE数据集和Harvard数据集上的性能。分别从两个数据集的20%测试集中随机选择一幅图像,其重建图像(上排)和误差图像(下排)如图 7和图 8所示。视觉上看,各种算法的重建结果差别微乎其微,但从局部细节放大图上看,DHSR算法在局部细节上的恢复明显有更大优势。

图 7 各算法在CAVE数据集上的重建图像和误差图像
Figure 7. The reconstructed and error maps on CAVE dataset by the different algorithms

图 8 各算法在Harvard数据集上的重建图像和误差图像
Figure 8. The reconstructed and error maps on Harvard dataset by different algorithms
从图 7c和图 7d中观察到,CSTF和BSR的误差图像中均出现了明显阴影。图 8为不同算法在Harvard数据集上的重建结果以及误差图像。从重建图像的细节放大图中可以看出,CSTF和BSR算法的重建图像都出现了局部细节丢失问题;而CNMF的重构图像在整体上取得了良好的性能,但是在误差图像的局部区域能看到关于草地的阴影,这可能是由于将3维数据展开成2维形式导致了结构信息的丢失;DHSR算法无论从整体上还是局部细节上都表现出更好的重构性能;此外,从误差图像中可以看出,该算法的误差图像和参考图像更加接近。
从重建图像和误差图像中只能直观观察到各种算法的重建效果,无法定量描述各种算法的性能差异,表 1和表 2显示了各种算法在信噪比分别为30 dB和35 dB的情况下在多种评价指标上测试集的平均性能差异。粗体字为最优值。如表 1所示,本文作者提出的DHSR算法在高光谱图像和多光谱图像的信噪比均为30 dB的条件下,RSNR分别比CSTF和CNMF提升了1.8 dB与1.9 dB;在RMSE指标中,提出的DHSR算法相比于CNMF降低了16%;当噪声减少时,各种算法在重建性能上明显取得了一定程度上的提升。在Harvard数据集上,当信噪比均为35 dB时,本文作者提出的DHSR算法比次优算法CNMF提升了2.2 dB;RMSE误差降低了30%;此外,DHSR算法在SAM上也取得了明显的性能提升,这表示本文作者提出的模型在重建图像中有明显更小的光谱畸变。
表 1 CAVE数据集中20%图像测试结果的平均性能
Table 1. Average performance of test results for 20% of the images in the CAVE dataset
algorithm case 1(SNR: 30 dB) case 2(SNR: 35 dB) ERGAS RSNR RMSE SAM SSIM ERGAS RSNR RMSE SAM SSIM SRTR 2.84 25.92 0.10 0.148 0.81 2.84 25.92 0.11 0.148 0.81 CSTF 2.00 28.93 0.08 0.096 0.87 1.52 31.33 0.06 0.065 0.89 BSR 2.72 26.23 0.11 0.121 0.90 2.70 26.31 0.10 0.121 0.90 CNMF 2.03 28.81 0.08 0.084 0.89 1.51 31.38 0.05 0.059 0.93 NLSTF 2.75 26.19 0.10 0.157 0.83 1.65 30.61 0.06 0.097 0.91 DHSR 1.61 30.68 0.06 0.069 0.95 1.05 34.16 0.04 0.046 0.97 表 2 Harvard数据集中20%图像测试结果的平均性能
Table 2. Average performance of test results for 20% of the images in the Harvard dataset
algorithm case 1(SNR: 30 dB) case 2(SNR: 35 dB) ERGAS RSNR RMSE SAM SSIM ERGAS RSNR RMSE SAM SSIM SRTR 2.95 23.47 0.14 0.064 0.90 2.95 23.47 0.14 0.064 0.90 CSTF 4.64 20.64 0.19 0.074 0.75 4.32 20.57 0.20 0.073 0.79 BSR 4.15 20.05 0.21 0.074 0.87 4.15 20.05 0.21 0.074 0.87 CNMF 2.54 25.38 0.11 0.047 0.89 2.00 27.18 0.09 0.037 0.94 NLSTF 3.57 23.87 0.13 0.066 0.86 2.51 25.77 0.11 0.05 0.92 DHSR 2.43 27.62 0.08 0.039 0.92 1.76 29.35 0.06 0.031 0.95 通过使用基于深度神经网络的自适应特征提取,可以有效捕获数据集中图像的自适应特征;将神经网络提取到的自适应先验特征以正则项的方式整合到优化问题中,可以有效提升重建图像的空间分辨率,同时降低光谱畸变现象。
高光谱图像和普通的光学图像的主要区别是:高光谱图像有多个光谱通道。上述性能数据表格描述了融合算法的整体性能,而图 7和图 8的误差图像只能反映一些波段的性能。为了进一步验证评估算法在多个谱带上的重建性能,并有效反映其对每个谱带的重建能力,分别从CAVE数据集和Harvard数据集的20%测试集中随机选择一幅图像,在输入图像信噪比均为35 dB的情况下,评估不同算法在各个谱带上的ERGAS、RMSE以及RSNR性能,如图 9和图 10所示。从图中可以看出,在CAVE数据集中,所提出的DHSR算法在所有谱带上的性能均显著领先。在Harvard数据集中,DHSR算法在大部分谱带上也领先于基准算法。实验结果证实了本文作者提出模型的合理性。通过引入基于深度神经网络的自适应先验特征正则化,在有效提升重构图像质量的同时,大幅度抑制了噪声的干扰。
-
DHSR算法的运算复杂度主要包括$ \tilde{\boldsymbol{Z}}$的估计以及利用ADMM对式(10)的迭代求解。首先,利用深度神经网络对先验特征$ \tilde{\boldsymbol{Z}}$的估计主要取决于神经网络的复杂度。当网络训练完成且观测图像已知时,可以直接获取图像对应的先验特征,因此该过程可视为数据预处理过程。式(10)的求解主要包含式(12)~式(14)的计算复杂度,且计算复杂度主要集中于式(12)和式(13),它们的运算复杂度分别为$ O\left(N_{\mathrm{a}} N_{\mathrm{w}}{ }^2 N_{\mathrm{h}}{ }^2\right)$和$ O\left(N_{\mathrm{a}}^2 N_{\mathrm{w}} N_{\mathrm{h}}\right)$。因此,DHSR算法的总体计算复杂度为$ O\left(N_{\mathrm{a}} N_{\mathrm{w}}^2 N_{\mathrm{h}}^2+N_{\mathrm{a}}^2 N_{\mathrm{w}} N_{\mathrm{h}}\right)$)。为了定量分析提出的DHSR算法和基准算法在实际运算中的复杂度,测试了各种算法的运行时间,如表 3所示。从表中可以看出,DHSR算法在两个数据集上的运行时间都领先于其它算法,主要原因是DHSR算法不涉及矩阵分解或者张量分解,不需要使用交替优化(alternating optimization,AO)对优化问题进行解耦,因此大幅度提升了算法的运行效率。
表 3 在信噪比为35dB时算法在不同数据集上的运行时间
Table 3. Algorithm running time on different datasets at SNR of 35 dB
dataset time/s SRTR CSTF BSR CNMF NLSTF DHSR CAVE 206.48 144.39 621.44 307.86 585.94 98.63 Harvard 209.92 155.52 677.88 316.48 746.69 94.27 -
提出了一种基于深度图像先验的高光谱图像超分辨率算法,该算法利用基于深度神经网络的自适应特征提取,可以有效捕获数据集图像的自适应特征,不仅可以低运算复杂度地提升高光谱图像的空间分辨率,而且可以有效抑制噪声的干扰。在CAVE和Harvard数据集上进行的实验测试结果证明了所提出的DHSR算法的可行性,经重建图像、误差图像、性能数据和光谱曲线对比,DHSR算法能够降低融合图像的光谱畸变,重建出与参考图像的空间和光谱结构一致的目标图像,证实了CNN与transformer结合可以同时提取图像的高频信息和低频信息先验。
基于自适应深度先验的高光谱图像超分辨率
Adaptive deep prior for hyperspectral image super-resolution
-
摘要: 为了解决现有的高光谱超分辨率方法依赖于手工先验和数据驱动先验会导致参数选择困难或可解释性差的问题,采用一种基于自适应深度先验正则的高光谱图像超分辨率方法,进行了理论分析和实验验证。首先设计基于卷积神经网络的多阶段特征提取网络,提取退化图像的空间和光谱信息;其次将提取到的空-谱先验输入基于transformer模型的特征融合模块;然后自适应交互空域和谱域的互补信息,以捕获图像的全局先验特征;最后在退化模型中插入深度先验正则项,将超分辨率问题表述为一个优化问题,其解可以通过交替方向乘子法获得并降低求解复杂度。结果表明,所提出算法在信噪比均为35 dB时,重建信噪比分别达到了34.16 dB和29.35 dB, 比次优算法高出2.78 dB和2.17 dB,重建的高分辨率高光谱图像与其固有结构具有较高的一致性。该研究为综合利用手工先验和数据驱动先验增强高光谱图像空间分辨率提供了参考。Abstract: To address the issue that the difficult parameter selection or poor interpretability caused by the existing hyperspectral super-resolution methods rely on manual or data-driven prior, a deep prior regularization-based hyperspectral image super-resolution method was adopted for theoretical analysis and experimental validation. First, a multi-stage feature extraction network based on a deep convolutional neural network was designed to extract spatial and spectral information from the degraded images. Then, the collected spatial-spectral prior features were fed into a transformer-based feature fusion module, where complementary information from the spatial and spectral domains was adaptively extracted to capture the image' s global prior features. Finally, the super-resolution problem of the image was formulated as an optimization problem by inserting deep prior regularization term in the degraded model, the solution of which can be achieved using the alternating direction method of multipliers while minimizing solution complexity. Experimental results show that reconstruction signal-to-noise ratio of this algorithm is 34.16 dB and 29.35 dB when both of the signal-to-noise ratio are 35 dB, which is 2.78 dB and 2.17 dB higher than the suboptimal algorithm, respectively. The reconstructed high-resolution hyperspectral images have high consistency with their inherent structures under the condition of deep prior regularization. This study provides a reference for the combined use of manual and data-driven prior to enhance the spatial resolution of hyperspectral images.
-
表 1 CAVE数据集中20%图像测试结果的平均性能
Table 1. Average performance of test results for 20% of the images in the CAVE dataset
algorithm case 1(SNR: 30 dB) case 2(SNR: 35 dB) ERGAS RSNR RMSE SAM SSIM ERGAS RSNR RMSE SAM SSIM SRTR 2.84 25.92 0.10 0.148 0.81 2.84 25.92 0.11 0.148 0.81 CSTF 2.00 28.93 0.08 0.096 0.87 1.52 31.33 0.06 0.065 0.89 BSR 2.72 26.23 0.11 0.121 0.90 2.70 26.31 0.10 0.121 0.90 CNMF 2.03 28.81 0.08 0.084 0.89 1.51 31.38 0.05 0.059 0.93 NLSTF 2.75 26.19 0.10 0.157 0.83 1.65 30.61 0.06 0.097 0.91 DHSR 1.61 30.68 0.06 0.069 0.95 1.05 34.16 0.04 0.046 0.97 表 2 Harvard数据集中20%图像测试结果的平均性能
Table 2. Average performance of test results for 20% of the images in the Harvard dataset
algorithm case 1(SNR: 30 dB) case 2(SNR: 35 dB) ERGAS RSNR RMSE SAM SSIM ERGAS RSNR RMSE SAM SSIM SRTR 2.95 23.47 0.14 0.064 0.90 2.95 23.47 0.14 0.064 0.90 CSTF 4.64 20.64 0.19 0.074 0.75 4.32 20.57 0.20 0.073 0.79 BSR 4.15 20.05 0.21 0.074 0.87 4.15 20.05 0.21 0.074 0.87 CNMF 2.54 25.38 0.11 0.047 0.89 2.00 27.18 0.09 0.037 0.94 NLSTF 3.57 23.87 0.13 0.066 0.86 2.51 25.77 0.11 0.05 0.92 DHSR 2.43 27.62 0.08 0.039 0.92 1.76 29.35 0.06 0.031 0.95 表 3 在信噪比为35dB时算法在不同数据集上的运行时间
Table 3. Algorithm running time on different datasets at SNR of 35 dB
dataset time/s SRTR CSTF BSR CNMF NLSTF DHSR CAVE 206.48 144.39 621.44 307.86 585.94 98.63 Harvard 209.92 155.52 677.88 316.48 746.69 94.27 -
[1] 刘煊, 渠慎明. 低秩稀疏和改进SAM的高光谱图像误标签检测[J]. 激光技术, 2022, 46(6): 808-816. doi: 10.7510/jgjs.issn.1001-3806.2022.06.016 LIU X, QU Sh M. False label detection in hyperspectral image based on low rank sparse and improved SAM[J]. Laser Technology, 2022, 46(6): 808-816(in Chinese). doi: 10.7510/jgjs.issn.1001-3806.2022.06.016 [2] 臧传凯, 沈芳, 杨正东. 基于无人机高光谱遥感的河湖水环境探测[J]. 自然资源遥感, 2021, 33(3): 45-53. ZANG Ch K, SHEN F, YANG Zh D. Aquatic environmental monitoring of inland waters based on UAV hyperspectral remote sensing[J]. Remote Sensing for Natural Resources, 2021, 33(3): 45-53(in Chinese). [3] 刘翠连, 陶于祥, 罗小波, 等. 混合卷积神经网络的高光谱图像分类方法[J]. 激光技术, 2022, 46(3): 355-361. doi: 10.7510/jgjs.issn.1001-3806.2022.03.009 LIU C L, TAO Y X, LUO X B, et al. Hyperspectral image classification based on hybrid convolutional neural network[J]. Laser Techno-logy, 2022, 46(3): 355-361(in Chinese). doi: 10.7510/jgjs.issn.1001-3806.2022.03.009 [4] YOKOYA N, YAIRI T, IWASAKI A. Coupled nonnegative matrix factorizationunmixing for hyperspectral and multispectral data fusion[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 50(2): 528-537. [5] YANG F X, PING Z L, MA F, et al. Fusion of hyperspectral and multispectral images with sparse and proximal regularization[J]. IEEE Access, 2019, 7: 186352-186363. doi: 10.1109/ACCESS.2019.2961240 [6] AHMAD T, LYNGDOH R B, ANAND S S, et al. Robust coupled non-negative matrix factorization for hyperspectral and multispectral data fusion[C]//2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS. New York, USA: IEEE Press, 2021: 2456-2459. [7] KANATSOULIS C I, FU X, SIDIROPOULOS N D, et al. Hyperspectral super-resolution: A coupled tensor factorization approach[J]. IEEE Transactions on Signal Processing, 2018, 66(24): 6503-6517. doi: 10.1109/TSP.2018.2876362 [8] MA F, HUO S, YANG F X. Graph-based logarithmic low-rank tensor decomposition for the fusion of remotely sensed images[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 11271-11286. doi: 10.1109/JSTARS.2021.3123466 [9] HU J F, HUANG T Zh, DENG L J, et al. Hyperspectral image super-resolution via deep spatiospectral attention convolutional neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 33(12): 7251-7265. [10] XIAO J J, LI J, YUAN Q Q, et al. Physics-based GAN with iterative refinement unit for hyperspectral and multispectral image fusion[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 6827-6841. doi: 10.1109/JSTARS.2021.3075727 [11] HU J F, HUANG T Zh, DENG L J, et al. Fusformer: A transformer-based fusion network for hyperspectral image super-resolution[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. [12] WU H P, XIAO B, CODELLA N, et al. Cvt: Introducing convolutions to vision transformers[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. New York, USA: IEEE Press, 2021: 22-31. [13] HE A, LI T, LI N, et al. CABNet: Category attention block for imbalanced diabetic retinopathy grading[J]. IEEE Transactions on Medical Imaging, 2020, 40(1): 143-153. [14] LI Zh W, SUI H, LUO C, et al. Morphological convolution and attention calibration network for hyperspectral and LiDAR data classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2023, 16: 5728-5740. doi: 10.1109/JSTARS.2023.3284655 [15] PAN H D, GAO F, DONG J Y, et al. Multiscale adaptive fusion network for hyperspectral image denoising[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2023, 16: 3045-3059. doi: 10.1109/JSTARS.2023.3257051 [16] 王龙光, 郭裕兰, 林再平, 等. 基于Transformer的高光谱图像超分辨率重建[J]. 中国科学: 信息科学, 2023, 53(3): 500-516. WANG L G, GUO Y L, LIN Z P, et al. Deep hyperspectral image super-resolution with transformers[J]. Scientia Sinica: Informationis, 2023, 53(3): 500-516(in Chinese). [17] SUI L Ch, LI L, LI J, et al. Fusion of hyperspectral and multispectral images based on a Bayesian nonparametric approach[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12: 1205-1218. doi: 10.1109/JSTARS.2019.2902847 [18] CHAI T, DRAXLER R R. Root mean square error (RMSE) or mean absolute error (MAE)-Arguments against avoiding RMSE in the literature[J]. Geoscientific Model Development, 2014, 7(3): 1247-1250. doi: 10.5194/gmd-7-1247-2014 [19] JIANG J J, SUN H, LIU X M, et al. Learning spatial-spectral prior for super-resolution of hyperspectral imagery[J]. IEEE Transactions on Computational Imaging, 2020, 6: 1082-1096. doi: 10.1109/TCI.2020.2996075 [20] LI Q, YUAN Y, JIA X P, et al. Dual-stage approach toward hyperspectral image super-resolution[J]. IEEE Transactions on Image Processing, 2022, 31: 7252-7263. [21] WANG Zh, BOVIK A C, SHEIKH H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. [22] YASUMA F, MITSUNAGA T, ISO D, et al. Generalized assorted pixel camera: postcapture control of resolution, dynamic range, and spectrum[J]. IEEE Transactions on Image Processing, 2010, 19(9): 2241-2253. [23] CHAKRABARTI A, ZICKLER T. Statistics of real-world hyperspectral images[C]//CVPR 2011. New York, USA: IEEE Press, 2011: 193-200. [24] WEI Q, BIOUCAS-DIAS J, DOBIGEON N, et al. Hyperspectral and multispectral image fusion based on a sparse representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(7): 3658-3668. [25] LI Sh T, DIAN R W, FANG L Y, et al. Fusing hyperspectral and multispectral images via coupled sparse tensor factorization[J]. IEEE Transactions on Image Processing, 2018, 27(8): 4118-4130. [26] DIAN R W, FANG L Y, LI Sh T. Hyperspectral image super-resolution via non-local sparse tensor factorization[C]//Proceedings of the IEEE Conference on Computer Vision and Pattem Recognition. New York, USA: IEEE Press, 2017: 5344-5353. -


 网站地图
网站地图

 下载:
下载: