-
微纳光纤[1](optical microfiber, OM)是一种新型功能光纤,直径在微米或亚微米量级,较多能量以倏逝场[2]形式存在于光纤物理边界之外,对外界环境较为敏感,被广泛应用于光纤传感领域[3]。针对微纳光纤的传输特性[4]、温度特性[5-6]、能量分布特性[7]等理论分析,为以微纳光纤为基础的耦合器[8]、谐振环[9]、光纤光栅[10]等器件的进一步研究提供了支持。目前,复合型微纳光纤成为研究热点,如光子晶体微纳光纤[11]、石墨烯复合微纳光纤[12]等。无论微纳光纤传感器或微纳光纤功能器件,直径对其影响都很大。但是,在制备微纳光纤的过程中,光纤直径由125μm下降到微米量级,变化了近100倍,单位长度上光纤体积变化近10000倍,难以精确控制微纳光纤直径。2014年, YU等人[13]利用LP02模截止条件,分析对应模间干涉的突变位置,作为微纳光纤直径的判断依据, 从而可将制备微纳光纤的直径误差降至2%左右。2015年,KELOTH等人[14]利用微纳光纤耦合光栅,组成复合微腔, 由该复合腔谐振波长与微纳光纤直径的关系, 可以反推微纳光纤的直径,实现光纤直径的无损和原位测量, 对于350nm~600nm直径的微纳光纤, 测量精度可以达到10nm。2020年, KANG等人[15]利用光纤透射强度的突变,根据微纳光纤直径对应的TE01模截止点,实时反馈控制光纤制备过程, 在360nm~680nm微纳光纤直径范围内, 实现了2nm的控制精度。
分析光纤拉制过程可知,电机位置误差、光纤自身重力、气流对拉制过程的影响等因素[16],会对微纳光纤外形造成影响,从而造成光纤直径一致性差,难以批量生产[17]。基于此,本文中提出了液体浸没强度检测方案,对微纳光纤-液体形成的圆柱形波导结构进行数值仿真,并搭建了实验系统对微纳光纤直径进行测试。
-
目前,常用的微纳光纤制备方法有化学腐蚀法[18]、化学生长法[19]、火焰扫描法[1]等,其中应用较为广泛的是火焰扫描法。本文中采用电加热扫描法拉制微纳光纤,拉制系统如图 1所示。利用陶瓷电加热头将普通单模光纤加热至熔融状态,此时利用程序控制电机向相反方向缓慢拉伸,最终拉制出不同外形的微纳光纤,其两端与普通光纤便于熔接。
由参考文献[20]可知,根据拉锥过程中的体积守恒和长度守恒两个规律,当加热区域随拉伸长度线性变化时,即L=L0+αx, 其中L0为初始加热区域长度,α为线性变化因子,x为移动平台总位移, L为随x线性变化的加热区域长度。设微纳光纤起始处为0,沿微纳光纤纵向为z方向,x′为0~x之间的变化量,则有:
$ r_{\mathrm{w}}(x)=r_{0} \exp \left(-\frac{1}{2} \int_{0}^{x} \frac{\mathrm{d} x^{\prime}}{L_{0}+\alpha x^{\prime}}\right)=r_{0}\left(1+\frac{\alpha x}{L_{0}}\right)^{-\frac{1}{2 \alpha}} $
(1) 式中,r0为单模光纤半径,rw为均匀区域微纳光纤半径。
此时,$z(x)=\frac{1}{2}(1-\alpha) x$,可得微纳光纤过渡区域的外形公式:
$ r(z)=r_{0}\left[1+\frac{2 \alpha z}{(1-\alpha) L_{0}}\right]^{-\frac{1}{2 \alpha}} $
(2) 式中,r(z)为过渡区域在位置z处的半径,进而可求得整根微纳光纤外形随纵向变化的关系。
本文中使用液体浸没强度法检测所拉制微纳光纤的直径,将微纳光纤浸没入液体之中,则会形成微纳光纤-液体的圆柱形波导结构,单模光纤中传输的基模在通过过渡区域时,需要考虑模式耦合问题,依据过渡区域绝热理论[21-22],采用判据为:
$ {\mathit{\Omega}} \leqslant \frac{a\left(\beta_{1}-\beta_{2}\right)}{2 \pi} $
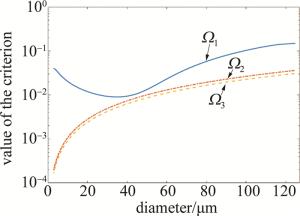
(3) 式中,Ω为过渡区域锥角正切值的绝对值,a为光纤半径,β1和β2为相互耦合两个模式的传播常数(微纳光纤对称分布,只考虑HE11与HE12耦合),再结合过渡区域的形貌公式及导波模的特征函数,即可判断过渡区域是否符合绝热条件。取均匀区域长度为10mm,线性变化因子为0.2,直径分别取2.7μm和4μm,由(3)式可得如图 2所示的变化曲线。其中,横坐标表示直径的大小,单位为μm; 纵坐标表示判据的值,没有单位; Ω1表示基模传输时相邻两个模式传播常数之差与2π之比随微纳光纤直径的变化,Ω2和Ω3分别表示直径为2.7μm和4μm时Ω随微纳光纤直径的变化。Ω2和Ω3始终在Ω1的下方,以上判据成立,可忽略模式耦合对结果的影响。
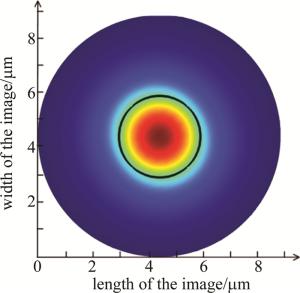
若微纳光纤直径为2.7μm、均匀区域长度为10mm、线性变化因子[20]为0.2、微纳光纤折射率为1.458、入射波长为1.55μm、液体折射率为1.36、液体吸收系数为0.38/mm(对应的液体是酒精)时,可使用COMSOL软件仿真微纳光纤-液体结构的波导传播常数,其虚数部分决定了微纳光纤的附加损耗,仿真可得纵向传输光场横截面上的能量分布, 如图 3所示。图中横、纵坐标用以标识微纳光纤物理边界,黑色实线为微纳光纤的物理边界,可知部分能量以倏逝场形式在液体中传输,而液体将对这部分能量产生吸收作用,从而导致微纳光纤产生附加损耗。
显然,微纳光纤均匀区域和过渡区域都将引入附加损耗,均匀区域直径不变,引入的附加损耗计算较简单,而过渡区域直径不断变化,可将该区域分为n等份,每一份可视作均匀柱状波导结构,根据上面所述方法,可以得到其复传播常数值,实部对光场传播起相位延时作用,虚部对光场传播起衰减作用,则第m等份单位长度上对应的附加损耗为:
$ L_{m}=-10 \lg \left(\mathrm{e}^{-2 \beta_{2 m}}\right) $
(4) 式中,β2m是该段复传播常数的虚数部分,Lm的单位是dB/mm,乘以该等份的长度即可得到该等份对应的附加损耗值,而整根微纳光纤对应的总损耗是所有等份附加损耗的和。
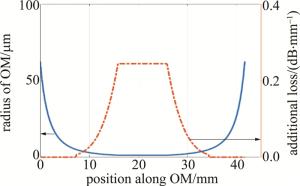
依据上面所述原理,可得微纳光纤外形尺度范围内对应的附加损耗值,如图 4所示。图中实线部分是根据上面所述拉制参量取直径为2.7μm时得到的微纳光纤外形直径分布,虚线部分是不同直径处对应的附加损耗大小。当直径为2.7μm时,其附加损耗约为0.22dB/mm,随着直径的增大,附加损耗值迅速减小; 当外形直径为15μm时,其附加损耗仅为0.01dB/mm。取直径参量为4μm时也可得到相似的外形直径分布以及各点损耗,当直径为4μm时, 其附加损耗值约为0.08dB/mm。
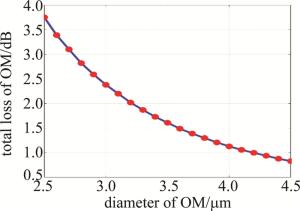
如图 5所示,通过对微纳光纤不同纵向位置处损耗的累加,即可得到由于微纳光纤浸没入液体所引入的总损耗值。图 5中横坐标表示微纳光纤的均匀区域直径,纵坐标表示微纳光纤对应的总损耗,计算过程中,其它参量同前。可以看到,当微纳光纤均匀区域直径为2.5μm时,对应的总损耗值为3.75dB,随着直径的增大,总损耗值将不断减小,当光纤直径为2.7μm时,总损耗值为3.10dB,当光纤直径为4μm时,总损耗值为1.13dB。这样,根据微纳光纤浸入液体后引入的总损耗值,即可反推得到微纳光纤直径的实际结果。
-
分别拉制4根参量相同的微纳光纤(参量如上面仿真所述,直径取2.7μm),如图 6所示。上半部分为实验制备的微纳光纤,下半部分为其在尼康LV100D显微镜(最小可读数为0.1μm)下的图像,可见制备的微纳光纤表面光滑直径均匀,且微纳光纤直径测得值均在2.7μm左右。
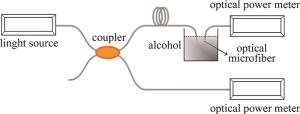
搭建微纳光纤直径测试实验系统,如图 7所示。驱动器(THORLABS CLD1015)控制分布式反馈激光器(distributed feedback laser, DFB)光源发出波长为1550nm的激光,经过3dB耦合器分束为两路,一路连接微纳光纤(可浸入酒精)后连接光功率计1(JOINWIT JW3208),一路直接连接光功率计2(型号同上)作为参考光,从而消除光源功率波动对测试结果的影响。
搭建好实验系统后,首先将第1根微纳光纤连入系统,测得初始功率值,然后将微纳光纤浸入酒精得到第2次出射功率值,将微纳光纤从酒精中取出,待酒精彻底挥发后,得到第3次出射功率值,根据初始功率值和浸入酒精后的出射功率值之间的比例关系,即可得到浸入液体后所引入的总损耗值。接着分别对第2根、第3根和第4根微纳光纤重复以上操作,可得如表 1所示的实验结果。
Table 1. Experimental results 1
initial power/mW power after deep into alcohol/mW power after out of alcohol/mW total loss after deep into alcohol/dB No.1 3.90 1.86 3.90 3.21 No.2 4.00 2.00 3.99 3.01 No.3 3.41 1.76 3.39 2.87 No.4 3.70 1.83 3.68 3.06 由表 1可知, 每根微纳光纤的初始功率有所差异,这可能是由制备过程引入的,也可能是由实验过程中光纤熔接引入的;从酒精中取出微纳光纤后,出射功率值均基本恢复至初始功率值,说明使用酒精浸没法测试微纳光纤直径,不会损伤微纳光纤,且具有可重复性;实验中微纳光纤浸没入酒精液体,引入的总损耗值接近上面仿真计算结果3.10dB,说明拉制微纳光纤的直径与设计值基本相同;根据实验数据分析,使用参考臂消除光源功率波动后,系统损耗测试误差小于0.01dB,测试结果中对应的附加损耗差异应主要来源于微纳光纤直径的偏差。根据图 5所示的微纳光纤总损耗与直径对应关系,再利用表 1中得到的微纳光纤总损耗值,可以得到4根微纳光纤的实际直径分别为2.66μm,2.73μm,2.78μm和2.72μm,对应的直径偏移量分别为40nm,30nm,80nm和20nm,直径偏移率约为1.5%,1.1%,3.0%和0.7%。
为了进一步验证本文中所提测试方案的有效性,再拉制4根参量相同直径取4μm的微纳光纤,利用尼康LV100D显微镜测量可知, 4根光纤均为4μm左右,重复以上实验步骤可得如表 2所示的实验结果。
Table 2. Experimental results 2
initial power/mW power after deep into alcohol/mW power after out of alcohol/mW total loss after deep into alcohol/dB No.1 4.03 3.07 4.02 1.18 No.2 3.79 2.96 3.79 1.07 No.3 3.93 3.02 3.91 1.14 No.4 4.11 3.15 4.10 1.16 由表 2可知,当直径改为4μm时同样可以得到上面中的结论,且每根微纳光纤引入的总损耗值接近上面仿真结果1.13dB,利用表 2中的微纳光纤总损耗值以及图 5中微纳光纤总损耗与直径对应关系,可得4根微纳光纤的实际直径分别为3.94μm, 4.09μm, 3.99μm和3.97μm,对应的直径偏移量分别为60nm, 90nm, 10nm和30nm,直径偏移率约为1.5%, 2.3%, 0.3%和0.8%。
以上实验结果显示了较好的微纳光纤直径一致性,由于系统损耗测试误差约为0.01dB,对应的两种直径测试最小分辨率分别约为3nm和12nm,该结果与参考文献[13]~参考文献[15]中所述的直径测试灵敏度持平。根据上面理论分析,若本实验中测试所用的微纳光纤直径减小,则对应的总附加损耗值将会增加,理论上本测试方案的测试灵敏度会进一步提高。
-
本文中使用液体浸没法进行了微纳光纤直径检测,数值仿真计算了微纳光纤-液体柱状波导结构,得到了给定参量下微纳光纤总损耗和直径的对应关系,拉制出两组直径不同、其余拉制参量相同的微纳光纤,并搭建了实验测试系统。结果表明,微纳光纤总损耗与直径密切相关,微纳光纤直径为2.7μm时,最小可测直径偏移量约为3nm,直径偏移量最大为80nm,最小为20nm;微纳光纤直径为4μm时,最小可测直径偏移量约为12nm,直径偏移量最大为90nm,最小为10nm,实际直径结果与理想设计结果偏差量较小,验证了液体浸没法测试微纳光纤直径的有效性,同时说明了拉制系统制备光纤的精确性。
本文中所述测试方法简便易行、可操作性强、精度高,为微纳光纤直径控制提供了一种测试方案,为进一步改善制备工艺、推动微纳光纤实际应用提供了技术途径。
微纳光纤直径测试技术研究
Research on diameter measurement technology of optical microfiber
-
摘要: 为了测量微纳光纤直径, 采用了液体浸没强度检测法。首先对微纳光纤-液体圆柱形波导结构进行理论分析, 得到了整根微纳光纤附加损耗与外形参量的对应关系, 搭建了微纳光纤直径测试实验系统, 并对两组直径不同的微纳光纤进行了测试。结果表明, 直径为2.7μm时, 直径测试最小分辨率约为3nm, 4根微纳光纤的直径偏移量分别是40nm, 30nm, 80nm和20nm; 直径为4μm时, 直径测试最小分辨率约为12nm, 4根微纳光纤的直径偏移量分别是60nm, 90nm, 10nm和30nm, 有较好的直径一致性, 证明了液体浸没强度检测法的可行性。此研究对微纳光纤进一步走向实用提供了技术支持。Abstract: In order to measure the diameter of the optical microfibers (OMs), the liquid immersion intensity detection method was used. Firstly, the structure of OM-liquid cylindrical waveguide was analyzed theoretically, and the relationship between the additional loss and the shape parameters of the whole OM was obtained. Then, an experimental system was set up to test two groups of OMs with different diameters. The experimental results show that when the diameter was 2.7μm, the minimum resolution of diameter measurement is about 3nm and the diameter offsets of four OMs are 40nm, 30nm, 80nm and 20nm, respectively. When the diameter is 4μm, the minimum resolution of diameter measurement is about 12nm and the diameter offsets of four OMs are 60nm, 90nm, 10nm and 30nm, respectively. At the same time, the results showe well diameter consistency and verified the feasibility of liquid immersion intensity detection method. This research provided technical support for the further development of OMs.
-
Key words:
- optical devices /
- diameter measurement technology /
- intensity detection /
- microfiber
-
Table 1. Experimental results 1
initial power/mW power after deep into alcohol/mW power after out of alcohol/mW total loss after deep into alcohol/dB No.1 3.90 1.86 3.90 3.21 No.2 4.00 2.00 3.99 3.01 No.3 3.41 1.76 3.39 2.87 No.4 3.70 1.83 3.68 3.06 Table 2. Experimental results 2
initial power/mW power after deep into alcohol/mW power after out of alcohol/mW total loss after deep into alcohol/dB No.1 4.03 3.07 4.02 1.18 No.2 3.79 2.96 3.79 1.07 No.3 3.93 3.02 3.91 1.14 No.4 4.11 3.15 4.10 1.16 -
[1] TONG L, GATTASS R R, ASHCOM J B, et al. Subwavelength-diameter silica wires for low-loss optical wave guiding[J]. Nature, 2003, 426(6968): 816-819. doi: 10.1038/nature02193 [2] ZHENG Z W, REN W H, ZHAO C J, et al. Guiding and far-field radiation characteristics of micro/nano optical fiber[J]. Laser Technology, 2009, 33(5): 497-499(in Chinese). [3] KORPOSH S, JAMES S W, LEE S W, et al. Tapered optical fibre sensors: Current trends and future perspectives[J]. Sensors, 2019, 19(10): 2294. doi: 10.3390/s19102294 [4] CAI W D. Propagation characteristics of silicon-based micro-nano optical fiber[D]. Changsha: Hunan University, 2019: 20-32(in Chinese). [5] JIANG X Y, XIAO Y Y. Temperature characteristics of birefringence of polarization-maintaining micro/nanofiber[J]. Chinese Journal of Lasers, 2019, 46(8): 0806001(in Chinese). doi: 10.3788/CJL201946.0806001 [6] LIU Y G, ZHANG W. Temperature characteristics of micro-nanofiber bragg grating surrounded with liquids[J]. Laser & Optoelectronics Progress, 2017, 54(4): 040605(in Chinese). [7] ZHANG L, ZENG Y, CHEN G Q, et al. Energy distribution of wedge-shaped micro/nano fiber[J]. Laser Technology, 2015, 39(5): 689-693(in Chinese). [8] DING R, ZHU Y Q, YAO X T. Simulation of micronano fiber couplers based on fused drawing[J]. Laser Technology, 2018, 42(4): 462-465(in Chinese). [9] ZHANG X Y, QIAN Y H, ZHANG Z X. Refractive index sensing based on micro-nano fiber resonant ring[J]. Chinese Journal of Quantum Electronics, 2018, 35(5): 631-635(in Chinese). [10] LI J J, LIU Y, QU S L. Research progress of femtosecond laser micro-nano processing optical fiber functional devices[J/OL]. (2020-01-27)[2020-08-27]. http://kns.cnki.net/kcms/detail/31.1690.TN.20200512.1512.002.html(in Chinese). [11] LUO Y, MA J, ZHONG Y Ch. Fabrication of photonic crystal micro-fiber and its characteristics[J]. Laser Technology, 2015, 39(3): 312-315(in Chinese). [12] LIU Z L. Study on theoretical modeling and applications of hybrid microfiber devices[D]. Lanzhou: Lanzhou University, 2019: 58-127(in Chinese). [13] YU Y, ZHANG X L, SONG Zh Q, et al. Precise control of the optical microfiber tapering process based on monitoring of intermodal interference[J]. Applied Optics, 2014, 53(35): 8222-8228. doi: 10.1364/AO.53.008222 [14] KELOTH J, SADGROVE M, YALLA R, et al. Diameter measurement of optical nanofibers using a composite photonic crystal cavity[J]. Optics Letters, 2015, 40(17): 4122-4125. doi: 10.1364/OL.40.004122 [15] KANG Y, GONG J, XU Y X, et al. Ultrahigh-precision diameter control of nanofiber using direct mode cutoff feedback[J]. IEEE Photonics Technology Letters, 2020, 32(5): 219-222. doi: 10.1109/LPT.2020.2966804 [16] WEI Zh T, HOU D T, MIAO J S, et al. Precise control of optical microfiber diameter[J]. High Power Laser and Particle Beams, 2018, 30(7): 137-141(in Chinese). [17] MA Ch J, XU W F, LI J M, et al. Research progress of gas sensor based on microfiber evanescent field effects[J]. Laser & Optoelectronics Progress, 2015, 52(10): 100003(in Chinese). [18] ZHANG E J, SACHER W D, POON J K S. Hydrofluoric acid flow etching of low-loss subwavelength-diameter biconical fiber tapers[J]. Optics Express, 2010, 18(21): 22593-22598. doi: 10.1364/OE.18.022593 [19] MERKULOV I A, MELESHKO A V, WELLS J C, et al. Two growth modes of graphitic carbon nanofibers with herring-bone structure[J]. Physical Review, 2005, B72(4): 045409. [20] BIRKS T A, LI Y W. The shape of fiber tapers[J]. Journal of Lightwave Technology, 2002, 10(4): 432-438. [21] XU F. Optical fibre nanowire devices[D]. Southampton, UK: University of Southampton, 2008: 1-159. [22] LOVE J D, HENRY W M, STEWART W J, et al. Tapered single-mode fibres and devices. Part 1: Adiabaticity criteria[J]. IEE Proceedings, 1991, J138(5): 343-354. -


 网站地图
网站地图


 下载:
下载: