网站地图
-
飞机涡流又称尾流或尾涡，主要由翼尖涡构成。翼尖涡指由于机翼上下翼面气压差形成的在翼尖处自下而上翻滚的气流，它以翼尖为中心，高速旋转并向后、向下延伸[1-3]。飞机尾涡是影响飞行安全的重要因素，它会使进入涡流区的后机轻则失去控制，重则发生空难[4-5]。因此我国民航主管部门为飞行安全制定了严格的尾流间隔标准，并要求空中交通管制员(air traffic controller, ATC)严格执行[6-7]。但是随着航空运输业的高速发展，交通流量越来越大、空域容量越来越紧张，原有的尾涡间隔标准过于保守，已经成为制约民航运行效率的重要因素。因此越来越多的航空研究学者将目光投向了尾涡探测技术的研究，希望通过对尾涡的准确探测，缩减原有尾涡间隔标准，在保证飞行安全的前提下提升运行效率。
目前尾涡最主要的探测工具是多普勒激光雷达，法国LEOSPHERE公司、中国科学院安徽光学精密机械研究所、中国海洋大学和西南技术物理研究所等均在近年推出了专门用于飞机尾涡探测的多普勒激光雷达系统。但传统的多普勒激光雷达在距离高度指示(range height indicator, RHI)探测模式下获得风场数据的输出结果为RHI速度色块变化图，不便于空中交通管制员识别，如果能够通过计算机将多普勒激光雷达探测到的机场风场及雷达底层数据进行尾涡自动识别，并将识别结果用于辅助ATC决策，那么将能够在保证安全的前提下提升系统的运行效率。国内外对多普勒激光雷达尾涡识别方法的研究报道相对较少，2011年，HU等人提出一种基于多普勒谱特征的飞机尾涡识别方法，他们以尾涡多普勒谱的对称性、展宽性和幅值反比特性为主要特征实现了尾涡的有效识别[8]。但是，该识别方法识别率受限于多普勒谱特征的样本大小且识别流程较为冗余。
本文中以多普勒激光雷达RHI模式探测原理为基础，结合飞机尾涡的空气动力学机理和波形匹配理论，提出一种基于滑动窗口思想的尾涡识别算法, 并采用西南技术物理研究所研制的激光雷达进行实地探测试验，对该算法进行了验证，证明了该算法具有可行性。
-
尾涡变化可由激光雷达探测沿光束传播途径上运动的气溶胶粒子对激光脉冲产生的多普勒平移情况来刻画[9]。在近地阶段，飞机产生尾涡的强度取决于飞机重量、飞行速度和翼展等因素。根据尾涡速度的变化特点，传统的尾涡速度描述模型主要包括有Rankine vortex模型、Lamb-Oseen vortex模型、Hallock-Burnham vortex模型、Adapted vortex模型、Smooth blending vortex profile模型和Multiple scale vortex模型[10]等。GERZ(2002)，KÖPP(1994)，PROCTOR(1998)等人对Hallock-Burnham vortex的标准尾涡切向速度模型[11]进行了验证，认为该模型能精确描述摆脱地面效应后的飞机尾涡切向速度变化，因此用于对飞机产生的左右尾涡进行建模。模型表述如下：
$ {\mathit{\Gamma }_0} = \frac{{mg}}{{\rho v{b_0}}} $
(1) $ {v_{\rm{t}}}\left( r \right) = \pm \frac{{{\mathit{\Gamma }_0}}}{{2{\rm{ \mathsf{ π} }}r}}\frac{{{r^2}}}{{{r^2} + {r_{\rm{c}}}^2}} $
(2) 式中，Γ0表示尾涡初始强度，m为飞机进近时的重量，g为重力加速度常量，ρ为空气密度，v为飞机的进近速率，b0为尾涡的初始涡核间距，vt(r)为飞机尾涡的切向速率，r为尾涡横切面上点与涡核中心点之间的距离，rc=0.052b0表示尾涡涡核半径。
考虑到激光雷达设备在探测机场跑道上空的气溶胶粒子运动情况时，其设备的方位角度和扫描角度相对确定[12]。在激光波束垂直扫过尾涡时，会得到尾涡速度的瞬时切面分布，其扫描原理如图 1所示。
Figure 1. Schematic diagram of wake vortex measurement of laser radar
在理想条件下，尾涡涡环上各点切向速度模的大小是相等，由于在扫描过程中，尾涡切向速率vt(r)与雷达径向速率vr(r)间会形成扫描夹角，将尾涡的切向速度投影至雷达波束的扫描方向，则形成了雷达回波的尾涡径向速率，具体表述如下：
$ {v_{\rm{r}}}(r) = {v_{\rm{t}}}{\rm{(}}r){\rm{cos}}\delta = \pm \frac{{{\mathit{\Gamma }_0}}}{{2{\rm{ \mathsf{ π} }}r}}\frac{{{r^2}}}{{{r^2} + {r_{\rm{c}}}^2}}{\rm{cos}}\delta $
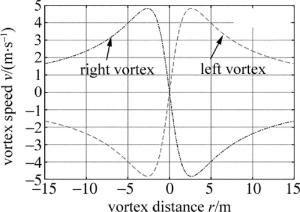
(3) 式中，δ为切向速率vt(r)与径向速率vr(r)之间的夹角。尾涡的雷达径向速度的变化趋势如图 2所示。
Figure 2. Relationship between radial velocity and distance of wake vortex
根据尾涡径向速度标准模型的变化趋势可知，左右尾涡的正负涡旋速度变化以涡核点为对称中心，且由于受到空气阻力的影响在无限远处其速度逐步趋近于零；当r趋近于涡核时，左右涡的径向速度值由于扫描夹角δ逐渐减小而增大，在涡核点附近达到最大值[13]，并在涡核点之后，速度出现突变。
-
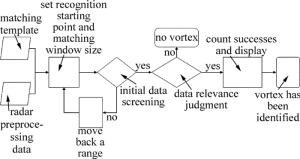
传统的尾涡识别方法直接根据雷达配套显示程序进行雷达径向速率图像显示，然后根据特征判断其是否为尾涡，不利于直观识别。因此，本文中根据飞机尾涡的波形特点，利用基于滑动窗口的相关系数法对雷达数据进行波形匹配，并根据阈值判断其是否为飞机尾涡，具体算法流程如图 3所示。
Figure 3. Flow chart of wake vortex waveform matching
根据流程图所示，尾涡波形匹配算法主要分为4个模块：(1)构建标准模板并对雷达数据进行处理。利用机型参量对尾涡切向速度进行建模，根据雷达与尾涡间的角度关系将标准尾涡的切向速度转化成雷达扫描方向的径向速度，并将之按单位步长进行离散化，形成标准径向速度匹配模板进而对雷达测得的回波速度进行匹配；(2)设置滑动窗口和步长。根据标准尾涡径向速度模型所生成的速度模板大小，选定匹配窗口和循环步长，对雷达数据进行遍历；(3)波形匹配。根据相关系数法原理对滑动窗口选定的数据样本与标准模板数据样本进行波形匹配，计算其相关系数；(4)尾涡数据判断。根据波形匹配所得出的相关系数与所设定的阈值参量进行比较：如果满足条件则判定该段数据为尾涡数据，否则将进行下一组数据匹配，直到完成所有筛选数据匹配。最后输出匹配结果，并且得出相应结论。
-
由于雷达数据样本容量大，单一的模板无法对整个数据进行匹配。为了快速准确的实现任意长度子序列的匹配识别，本文中采用基于滑动窗口的子序列匹配模式[14]。该方法可根据样本特征灵活设定滑动窗口大小，进而对整个样本序列进行局部特征识别提取。
在设置波形匹配程序时，需要对两个波形信号的相似程度进行描述。为描述波形的相似程度，引入了相关系数的概念，它是一个专门用来定量描述样本变量相似度的量。相关系数大小反映了序列间的相似程度[15]。相关系数表述公式如下：
$ {R^2} = \frac{{{\sigma _{xy}}}}{{{\sigma _x}{\sigma _y}}} $
(4) $ {\sigma _{xy}} = \frac{{\sum {\left[ {\left( {x - \overline x } \right)\left( {y - \overline y } \right)} \right]} }}{n} $
(5) $ {\sigma _x} = \sqrt {\frac{{\sum {{{\left( {x - \overline x } \right)}^2}} }}{n}} $
(6) $ {\sigma _y} = \sqrt {\frac{{\sum {{{\left( {y - \overline y } \right)}^2}} }}{n}} $
(7) 式中，x为标准模型速度样本变量，y为雷达数据的样本变量，n为样本容量，σx和σy分别为变量x和y的方差，σxy为变量x和y的协方差，R2为变量x和y的相关系数。
-
为了验证该算法的可行性，利用西南技术物理研究所研制的多普勒激光雷达在某机场所测得的波音747机型的起飞雷达观测数据为匹配样本，并利用该算法对雷达数据进行匹配识别验证。机型数据如表 1所示。
Table 1. Model parameters
type of aircraft B747 maximum take-off weight 416385kg take-off speed 83.3m/s span 64.4m air density 1.16kg/m3 gravity acceleration 9.81m/s2 多普勒激光雷达参量如表 2所示。
Table 2. Radar parameters
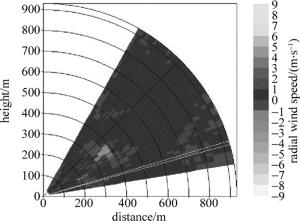
observation mode RHI detection range 45m~915m detection accuracy 30m scan angle range 10°~60° scan step length 1.0° 利用多普勒激光雷达实地探测飞机起飞时某瞬时径向风速回波变化情况，其中雷达进行RHI探测尾涡的一个典型结果如图 4所示。从图中可以看出, 异常速度出现的空间范围为300m~400m之间，该空间的局部速率变化达到±4m/s，且存在速度的对称突变，具有典型的尾涡特征。
Figure 4. Radar RHI display
因此根据雷达扫描的变化规律对雷达径向速度数据进行处理，利用尾涡识别算法根据尾涡径相速度标准模板对处理数据行波形匹配识别。在程序处理中将雷达数据匹配样本容量设置为30，且匹配样本值中绝对值最大值大于2.5作为数据筛选的阈值条件，并将R2>0.75作为匹配阈值。匹配结果如图 5所示。
Figure 5. Relationship between speed and distance after vortex wave matching
该匹配程序初步筛选了135组数据，共4050个数据，并进行尾涡波形匹配。根据尾涡匹配结果图可以看出，共识别出左涡5次，右涡4次，且左右尾涡的速率变化大致在±4m/s之间，并且波形对称，与标准模板基本符合。
为了检验识别率和虚警率，以雷达在RHI模式下的显示结果衡量其识别率。同时引入Kolmogorov-Smirnov(K-S)非参量检验方法的双样本检验对识别结果进行校验，其原理是对两个样本的经验累积分布函数进行比较来检验两个样本是否服从同一分布[16]，并以之为标准校验筛选数据中的虚警数目，从而确定虚警率。具体检验结果如表 3所示。
Table 3. Test results
total measured data 76440 filter data 4050 vortex type left vortex right vortex RHI display results 5 5 matching results 5 4 recognition rate 90% consistent with K-S test 3 3 number of false alarms 2 1 false alarm rate 3.70×10-4 从检验结果可以看出，该识别方法的识别结果基本符合RHI显示结果，其尾涡识别率达到90%，且虚警率为3.70×10-4。从上述结果可以看出，该识别程序具有较高的识别率和较低的虚警率，且能直观地显示其分析结果，并能提取相关的尾涡数据，以便进行进一步的尾涡分析。
-
以多普勒激光雷达探测原理为基础，结合飞机尾涡的空气动力学机理，建立飞机尾涡径向速度标准模型，引入波形匹配理论，提出了一种基于滑动窗口思想的尾涡识别算法。通过激光雷达在机场的实测数据验证分析，该方法有较高尾涡识别率和较低虚警率，在实际应用中有较高工程价值。由于在建模中未考虑气象环境变化因素，因此降低了其匹配度和识别率。在后续研究中将对其进行改进，进一步考虑大气背景场影响因素，从而提高尾涡识别率，为民航安全运行和效率提升提供有力保障。
多普勒激光雷达的飞机尾涡识别方法
Identification method of aircraft wake vortex based on Doppler lidar
-
摘要: 为了提高民航安全和飞行效率，实现对尾涡的准确识别，对飞机尾涡的空气动力学理论，特别是经典的Hallock-Burnham尾涡速度数学模型进行了分析研究。结合多普勒激光雷达探测涡流风场径向速度的原理，建立了雷达飞机尾涡探测的径向速度标准模型，引入滑动窗口思想，提出一种基于波形相似度匹配的方法，对尾涡进行自动识别，并给出了详细的算法流程；利用实测的激光雷达风场及雷达底层数据和假设检验方法对该识别方法进行了理论分析和实验验证。结果表明，该算法对飞机尾涡的有效识别率为90%。研究结果对进一步的尾涡监测具有一定参考价值。Abstract: In order to improve civil aviation safety and flight efficiency and realize accurate identification of wake vortex, aerodynamic theory of aircraft tail vortex, especially the classical Halock-Burnham wake velocity mathematical model was analyzed and studied.One standard radial velocity model for radar aircraft wake detection was established by using the principle of Doppler lidar to detect the radial velocity of vortex wind field.The idea of sliding window was introduced.A method based on waveform similarity matching was proposed to identify the wake vortex automatically.The detailed algorithm flow was also given.The recognition method is theoretically analyzed and experimentally verified by using the measured data of lidar wind field and the hypothesis testing method.The results show that the effective recognition rate of this algorithm for aircraft wake vortex is 90%.The results of the study have some reference value for further wake monitoring.
-
Table 1. Model parameters
type of aircraft B747 maximum take-off weight 416385kg take-off speed 83.3m/s span 64.4m air density 1.16kg/m3 gravity acceleration 9.81m/s2 
下载: 导出CSV
Table 2. Radar parameters
observation mode RHI detection range 45m~915m detection accuracy 30m scan angle range 10°~60° scan step length 1.0°
下载: 导出CSV
Table 3. Test results
total measured data 76440 filter data 4050 vortex type left vortex right vortex RHI display results 5 5 matching results 5 4 recognition rate 90% consistent with K-S test 3 3 number of false alarms 2 1 false alarm rate 3.70×10-4
下载: 导出CSV
-
[1] WEIMERSKIRCH H, MARTIN J, CLERQUIN Y, et al. Energy saving in flight formation[J]. Nature, 2001, 413(6857):697-698. doi: 10.1038/35099670 [2] CROW S C. Stability theory for a pair of trailing vortices[J]. AIAA Journal, 1970, 8(12):2172-2179. doi: 10.2514/3.6083 [3] IVANOV A V, LEBEDEV A V, OSTROVSKII L A, et al. Experimental investigation of the motion of laminar vortex pairs in a stratified fluid[J]. Fluid Dynamics, 1987, 22(2):322-325. doi: 10.1007/BF01052273 [4] MURPHY B, O'CALLAGHAN J, FOX M, et al. Overview of the structures investigation for the american airlines flight 587 investigation[C]//Structural Dynamics and Materials Conference. Washington DC, USA: American Institute of Aero-nautics and Astronautics, 2013: 3369-3373. [5] FEDERAL AVIATION ADMINISTRATION. Official accident investigation report[EB/OL]. (2009-2-25)[2018-2-13].http://asndata.aviation-safety.net/reports/2009/20090225-0_B738_TC-JGE.sheml. [6] INTERNATIONAL CIVIL AVIATION ORGANIZATION. Air regulations and air traffic services[DB/CD]. Beijing: Air Traffic Management Bureau of CAAC, 2000: 1-289. [7] INTERNATIONAL CIVIL AVIATION ORGANIZATION. Air traffic service manual (ICAO9426-AN/924)[DB/CD]. Beijing: Air Traffic Management Bureau of CAAC, 1999: 1-117. [8] XU Sh L, HU Y H, WU Y H. Identification of aircraft wake vortex based on Doppler spectrum features[J]. Journal of Optoelectronics·Laser, 2011, 22(12):1826-1830(in Chinese). [9] LI C, LIU J W, ZHAO P E, et al. Correction method of tilt wind field of mobile wind lidar[J]. Laser Techonlogy, 2017, 41(3):385-390(in chinese). [10] CHOROBA P. Comprehensive study of the wake vortex phenomena to the assessment of its incorporation to ATM for safety and capacity improvements[D]. Zilina, Slovak Republic: University of Zilina, 2006: 1-184. [11] FREHLICH R, SHARMAN R. Maximum likelihood estimates of vortex parameters from simulated coherent doppler lidar data[J]. Journal of Atmospheric & Oceanic Technology, 2005, 22(22):117-130. [12] HUANG J Ch, SUN Y W, XU Y, et al. Radar signal fast recognition based on the principle of time series comparability[J]. Electronic Information Warfare Technology, 2012, 27(5):1-5(in Chinese). [13] WU Y H, HU Y H, DAI D Ch, et al. Research on the technique of aircraft wake vortex detection based on 1.5μm Doppler lidar[J]. Acta Photonica Sinica, 2011, 40(6):811-817(in Chinese). doi: 10.3788/gzxb [14] HU Y H, WU Y H. Study on the characteristic of aircraft wake vortex and lidar detection technique[J]. Infrared & Laser Engineering, 2011, 40(6):1063-1069(in Chinese). [15] FENG J Zh, LIANG J Y, ZHENG S L, et al. Correlction coefficient method for vehicle road simulated load signal screening[J]. Journal of Mechanical Strength, 2018, 40(1):50-54(in Chinese). [16] QIAO X Q, CHEN D H, WANG Sh L. Joint estimation of modulation and SNR via method of moments and Kolmogorov-Smirnov test[J]. Journal of Information Engineering University, 2017, 18(4):399-402(in Chinese). -
点击查看大图
图(5) / 表(3)
计量
- 文章访问数: 6144
- HTML全文浏览量: 4145
- PDF下载量: 106
- 被引次数: 0
