网站地图
-
激光半主动寻的制导武器(laser semi-active search guide weapons，LSSGWS)具有制导精度高、抗干扰能力强、结构简单、成本低、使用方便等优点，因而被广泛应用于武器装备中，成为使用频率最高的光电精确制导武器[1-4]。半主动激光制导武器主要依靠武器前端的激光导引头起作用[5]。激光导引头由光学系统收集激光照射目标物体上反射的回波，利用位置敏感探测器(position sensitive detector，PSD)或者四象限探测器(quadrant detector，QD)等光学位置传感器进行制导。
采用10脉冲/s~20脉冲/s脉冲激光进行制导时，探测器多采用速度响应快的光学位置传感器，探测器会输出纳秒级的脉冲信号[6]。实际使用过程中，探测仪器性能要受到噪声及干扰的影响和限制。光学探测器主要的噪声来源包括热噪声、散粒噪声和闪烁噪声等[7]；干扰主要由暗电流、背景光等引起的。当激光制导过程中，目标的反射率低或者传输距离远时，光信号会更加微弱，这时就需要尽可能消除探测器上噪声和干扰的影响提取有用的信号以获得准确的光斑位置。
ZHAO[8]等人研究并实现了基于通用并行计算架构平台的快速傅里叶变换(fast Fourier transformation, FFT)并行计算，但是只局限于NVIDIA公司的统一通用并行计算架构平台。YIN[9]等人利用小波理论对PSD信号进行有用信号的提取，但是小波转换在常规处理器上实现很复杂。而采用FFT对光学位置探测器所获得的信号进行处理，不但可以有效地消除误差，增加光斑位置探测的精度，而且可以很方便地在弹载计算机上实现。但是常规的数字信号处理器(如数字信号处理器(digital signal processing, DSP)、先进精简指令集微处理器(advanced risc machine, ARM)、FFT处理器等)在处理速度及处理时间上都无法满足弹载计算机对时间及功耗的要求。ZHAN等人[10]利用现场可编程门阵列(field-programmable gate array, FPGA)实现了多路并行结构的FFT处理器，但是进行FPGA开发时，需要了解FPGA硬件开发的特定领域的知识，并且VHDL和Verilog硬件描述语言可移植性较低，在移植的过程中受到FPGA逻辑单元阵列数量的限制。
本文中提出了使用OpenCL实现FFT算法的方法，通过一个高级语言合成工具映射到片上系统(system on chip, SoC)-FPGA上实现OpenCL并行运行。该方法的主要优点是：(1)增加了FFT算法的高效性、可靠性，利用OpenCL在SoC-FPGA上实现并行FFT可以大大减少FFT算法的运行时间，利用FPGA实现硬件加速器，大大增加了算法运行的可靠性, 并且OpenCL具有“一次编写、各设备上运行”等优势，使得面向OpenCL的程序具有高度可移植性；(2)减少了实现机制的功耗和增加了便捷性，SoC-FPGA实现了硬核处理系统(hard proceisor system, HPS)性能(在设计中加入了随机存取存储器(random access memory, RAM)、只读存储器(read only memory, ROM)、串行外设接口(serial peripheral interface, SPI)、控制器局域网络(controll area network, CAN)等常用模块，极大扩展了SoC的应用领域，方便系统增加各类常用的传感器)的同时又兼顾低功耗的特性，这使得SoC-FPGA很适合作为数字信号处理器应用到激光半主动武器系统中。
-
为了增强激光发射器在大气中的峰值功率，一般激光发射器都会发射重频较低、脉宽较窄的脉冲光。直接照射到目标上经过目标的反射，被导引头的光学系统探测到并且光电位置探测器会产生相应的信号，并有相关数字信号处理电路，最后控制导弹的姿态并命中目标。光电位置传感器单一引脚经过单一I/V(电流/电压)转换后输出的波形如图 1中1通道波形所示。
Figure 1. The waveform of position sensor
输出波形的主要特点是：(1)由于背景光的影响，波形输出时有个直流变量，表现在图 1a中就是初始值并不是在零点位置；(2)消除背景光影响后在光强较强的情况下，波形完美可以进行数据采集，但是在光强较弱的情况下各种噪声比较多，原始信号几乎被泯灭在噪声中，表现在图 1c中就是几乎辨别不出原始信号；(3)周期T=10Hz~20Hz。所以就要求4路信号的运算在50ms~100ms之内完成，单路信号的运算在12.5ms~25ms之内完成。
-
由于FFT具有蝶型单元和组的概念等特点，所以对FFT算法进行并行化处理是快速、可靠的方法之一。MAIMAITIJIANG等人[11]研究了FFT算法并行计算的实现。SoC-FPGA不仅具有FPGA结构可方便实现FFT的并行操作，而且具有ARM处理器，很容易对数据进行管理和分配处理。
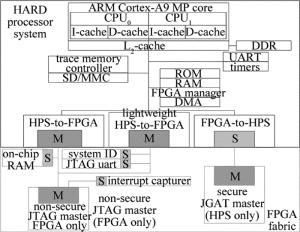
为了在SoC-FPGA实现并行FFT运算，需要在芯片内部进行外围电路和网络互连的协议(internet protocol, IP)核添加，图 2是添加完成后的主要系统框图。
Figure 2. Hardware architecture of SoC-FPGA for FFT
整个SoC-FPGA系统被分为两大区块：HPS和FPGA部分。对于HPS部分，主要是嵌入了ARM公司的ARM Cortex-A9处理器，加入RAM, ROM等内存IP是为了后续读取局部数据时需要，安全数码卡等外部FLASH是为了存储数据和程序。对于FPGA部分，加入了一些和HPS部分通讯和控制的总线和控制器，剩余部分主要还是沿袭了FPGA的系统结构，此处就不在重述。
为了更方便地实现FFT的并行化处理，选用OpenCL作为设计的主体语言，SoC-FPGA的OpenCL主要面向信号处理类应用的客户，是用C语言开发FPGA的新方法。而SoC-FPGA具有的并行和多核处理的架构非常适用于基于异构平台运行应用程序接口的OpenCL的运行。
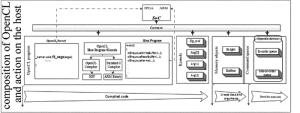
一个完整的OpenCL运行程序通常由两部分组成：一个宿主机程序和一个或多个内核组成的集合。宿主机程序是在宿主机(本次为ARM)上运行，内核在OpenCL设备上执行，它是完成整个OpenCL应用的具体工作。
图 3展示了作者设计的并行高速FFT的主要组成及基本工作流程。内核函数的设计会在接下来进行讨论。
Figure 3. Action of OpenCL in SoC-FPGA
-
FFT本身具有很好的分治特性，根据这个特点来研究它的并行性特征[12], 实现在SoC-FPGA平台的运行。
对N点序列x(n)，其离散傅里叶变换(discrete Fourier transform, DFT)的变换对定义为：
$ X\left( k \right) = \sum\limits_{n = 0}^{N - 1} {x\left( n \right)} {W_N}^{nk},{\rm{ }}\left( {k = 0,{\rm{ }}1,{\rm{ }} \cdots ,{\rm{ }}N - 1} \right) $
(1) $ x\left( n \right) = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {X\left( k \right){W_N}^{ - nk},{\rm{ }}} (n = 0,{\rm{ }}1,{\rm{ }} \cdots ,{\rm{ }}N - 1) $
(2) 式中, 旋转因子${W_N}^{nk} = {\rm{exp}}\left( { - {\rm{j}}\frac{{2{\rm{ \mathit{ π} }}}}{N}nk} \right)(n = 0,{\rm{ }}1,{\rm{ }} \cdots ,{\rm{ }}N - 1)$。COOLET和TUKEY在1965年利用W因子具有周期性及对称性(见(3)式)，提出用快速傅里叶变换算法, 使N点DFT的乘法计算量由N2次降为$\frac{N}{2}{\log _2}N$次。
$ \begin{array}{l} {W^0} = 1,{\rm{ }}{W^{N/2}} = - 1,\\ {W_N}^{N + r} = {W_N}^r,{\rm{ }}{W^{N/2 + r}} = - {W^r} \end{array} $
(3) 采样点为N时，按时间抽取基-2 FFT共需log2N级的蝶形运算，且每一级有N/2个蝶形运算。实现时先对输入采样点进行倒位序调整，再逐级作蝶形运算，最后得到正序的FFT输出。
由于FFT中每一级的蝶形运算存在相互独立性，根据蝶形运算的原理，引入并行执行的思想。
-
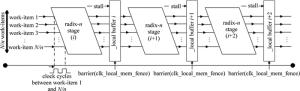
归并过程是整个FFT变换的核心。并行归并算法的初始思想就是将输入元素均匀的分布在处理机上[12]。对于具有N个采样点的FFT序列，需要M=log2N级来计算得到最终的输出结果。第1级先计算得到N/2个两两元素组成的FFT序列，第2级将前一级归并为N/4个元素的FFT序列，以此类推，直到求出最后的FFT序列。用OpenCL实现FFT的过程具体如图 4所示。
Figure 4. FFT for 64-element sequence with 4 work items
首先假设整个FFT运算可以划分为Q个工作项(Q < N)，并为2的幂，然后各个工作项独立计算FFT变换的前log2(N/Q)级，但是之后的(log2N-log2(N/Q)=log2Q)级需要各个工作项之间的运算操作必须同步化进行。图 4中假设x(n)有64个元素，很容易知道FFT需要进行6级运算，假设用4个工作项来进行并行处理，那么各个工作项需独立计算(log2(64/4)=4)级运算，然后在第4级运算完成后，同步各个工作项之间的处理结果，然后进行第5级和第6级运算。理想条件下，基-2 FFT(1-D)时间复杂度O可以下降到$O\left( {\frac{N}{Q}{{\log }_2}N} \right)$。
具体在SoC-FPGA上用OpenCL实现FFT并行计算时主要涉及到内核的硬件实现，实现过程是通过FPGA的软件开发工具包编译OpenCL的内核产生一个电阻晶体管逻辑电路项目，从而实例化一个宽的流水线结构。主机程序是按照初始化平台、寻找设备、打印设备信息、创建设备上下文、在设备上下文中创建指令队列、载入设备代码、编译设备代码、创建核函数对象、设置核函数参量、运行核函数、等待核函数运行结束、清除所有对象等流程进行编写[13]。内核的执行流程见图 5。工作项目流程是一个平行的流水线FFT加速器。已进入加速器的工作项目连续交错正好经历一个时钟周期，当工作项目之间需要数据交换时，必须停止当前的工作项目，在栅栏的作用下进行同步化，之后各个工作项目继续进行下一阶段的计算，直到整个项目完成。
Figure 5. Flow of N-D parallel FFT algorithm
整个FFT并行具体计算过程是：假设N点的数据序列，在进行FFT变换时，每级都需要经过N/2个蝶形运算；Kernel函数含有一个基-n FFT引擎，每一时钟周期能够处理n(n为2的幂)个数据点，这个引擎通过一个固定的顺序处理块(蝴蝶、旋转、交换、重新排序、乘法等)，产生n个输出点的FFT变换。在一个工作项目任务中，Kernel函数被设计为一个循环调用的过程。通过循环调用FFT引擎M次，最后将数据从设备端输出到主机端完成整个FFT变换。
本次设计每一时钟周期能够处理8个数据点的基-4 FFT内核主要框架如下：(1)设计FFT蝶型块、数据旋转块、数据交换块；(2)定义全局转换FFT的点数N=4096；(3)调用FFT蝶型块、数据旋转块、数据交换块；(4)接下来(log2N-2)阶段交替两个计算模式(在此之前要调用一次#pragma unroll来指示编译器完全展开循环以增加流水线并行性)；(5)最后(log2N-1)阶段就是移动滑动窗口内容，在此过程中如果编译器能够完全展开循环，硬件就可以将整个内容并行。
此内核函数被配置为作为单个工作项的内核，它使用一个滑动窗口来表示延迟元件。该内核函数在运行时首先从全局内存中读取输人数据，并将数据馈送到8个数据点的基-4 FFT内核然后将存储结果保存到全局内存。数据时顺序输入然后反比特输出，在编译时编译器利用流水线的并行性，通过重复FFT内核的源代码，进行循环的迭代，每一个时钟周期启动一次迭代。
-
为了和常规串行FFT进行对比，需要对设计的程序进行运算耗时的对比，主要是根据本次实验并结合FFT在进行1024和4096个元素的变换时在ARM[14-15], DSP[16-17]等处理器上的运行时间进行对比，具体结果见表 1，运算耗时是微处理器最重要的性能指标之一。分析表 1可知，具有NEON的ARM Cortex-A8平台在计算FFT时耗时最长，实时性最差，基于TI的C6713单核DSP运算平台对FFT实现性能次之。对于4096点复数数据的FFT并行运算耗时仅为6.0449ms，这主要是因为在并行FFT运算中需要进行多次同步化操作，而同步化很耗时间。对于实时性要求较高的数字信号处理的微处理器，SoC-FPGA完全满足性能的要求。
Table 1. Comparison of operation time of ARM, DSP and SoC-FPGA
processor family processor type points of FFT 1-D FFT/ms SoC-FPGA 5CSEA5 1024 1.3124 4096 6.0449 ARM ARM Cortex-A8
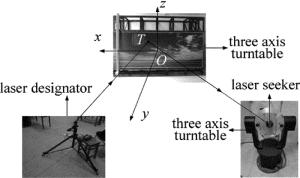
with NEON1024 15.2585 4096 59.0241 DSP TMS320C6713 1024 12.9487 4096 51.7513 为了验证本文中提出的方法，搭建实验室实验环境，具体如图 6所示。
Figure 6. Experiment of laser semi-active diffuse reflection
在实验室内，将激光指示器发射的激光照射到漫反射屏上，调整三轴转台，使固定在三轴转台上的导引头能接收到激光信息，利用数采卡进行数据采集。
将数据采集卡通道设置为4，采样率F=2000Hz，采集时间设置为10s。编写相关的程序并下载到目标板内，运行程序。
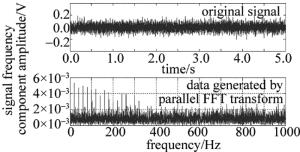
将原始数据和SoC-FPGA产生的数据进行绘图，如图 7所示。
Figure 7. Original signal and FFT transform result of laser semi-active photoelectric detector
在多级的归并运算过程中，数据的截尾会产生误差，影响运算的精度。但由于该误差较小，不影响后续频谱的分析和处理。首先根据所得数据，计算某点n所代表的频率Fn=(n-1)F/N。第1个点表示的是直流分量(即0Hz)，直流分量的存在主要是杂散光等环境因素造成的，所以在计算光斑点坐标时，首先是将第1个点的模值除以N，得到直流分量；之后根据n=FnN/F+1计算特定频率下的模值，再除以(N/2)得到原始信号的峰值，从而达到去除其它频率噪声的目的。最后也可根据FFT之后的坐标点计算相位关系。
对于4096点数据的FFT并行运算耗时为6.0449ms，由于并行FFT运算中需要进行多次同步化操作，而同步化很耗时间，所以对OpenCL程序进行进一步的优化设计，还可以得到更好的性能。对于实时性要求较高的激光半主动导引头的数字信号处理，SoC-FPGA完全满足性能的要求。
-
通过分析激光半主动导引头信号的特征，利用FFT算法的并行性和OpenCL并行编程的特点，实现FFT的并行计算方法，该方法运行在具有并行和多核处理架构的SoC-FPGA上。通过实验验证，在保证可以精确计算坐标数据量的前提下，本文中提出的运行于SoC-FPGA的OpenCL的并行FFT方法，其运行时间远小于单周期的激光信号，可以有充足的时间接下来进行其它操作。另外，考虑到SoC-FPGA和OpenCL未来广泛的应用领域，可以将现有的并行FFT计算方法与其在相关领域中的应用结合起来，进一步提高其应用价值。
基于激光导引头信号的并行高速FFT算法设计
Design of parallel high-speed FFT algorithm based on laser seeker signal
-
摘要: 为了减少激光半主动武器中测量光学器件光斑点坐标时噪声和干扰对探测精度影响、增加脉冲信号的测量带宽、提取信号的有效值，同时克服串行快速傅里叶变换（FFT）运算耗时及时间复杂度较大的问题，基于多核和并行架构的SoC-FPGA平台以及OpenCL软件，提出了实现并行FFT的计算方法。结果表明，利用该方法可使FFT（1-D）的时间复杂度下降到原来的1/Q，得到了较好的加速效果；通过3种平台（先进精简指令集微处理器、数字信号处理器和片上系统现场可编程门阵列）的运算耗时实验对比，该算法运算耗时为6.0449ms（1-D 4096点），要比同点数其它两种平台运算耗时少。并行FFT算法不仅满足激光半主动导引头信号实时性的要求，而且可以达到去噪的效果，能有效地降低噪声和背景光的影响。Abstract: In order to reduce the influence of noise and interference on the detection accuracy of optical spot coordinates in semi-active laser weapons, the measurement bandwidth of pulse signal increased and the effective value of the signal was extracted. By overcoming the great time-consuming and complexity of the serial fast Fourier transform (FFT) operation, parallel FFT computing method was proposed based on multi-core and parallel architecture system on chip-field-programmable gate array (SoC-FPGA) platform and OpenCL software. By this method, the time complexity of FFT (1-D) can be reduced to 1/Q times and the better acceleration effect was obtained. After comparing the computational time-consuming experiments of three platforms (advanced risc machines, digital signal processing and SoC-FPGA), the caculating time of the proposed algorithm is to 6.0449ms (1-D 4096 points) and less than that of the other two platforms with the same number of points. The results show that parallel FFT algorithm not only meets the requirement of the real-time performance of laser semi-active seeker and achieves the effect of denoising, but also can effectively reduce the influence of noise and background light.
-
Key words:
- measurement and metrology /
- parallel fast Fourier transform /
- SoC-FPGA /
- OpenCL /
- time complexity /
- laser semi-active
-
a—outside the darkroom with high intensity b—in the darkroom with high intensity c—in the darkroom with low intensity
Figure 1. The waveform of position sensor
Figure 7. Original signal and FFT transform result of laser semi-active photoelectric detector
Table 1. Comparison of operation time of ARM, DSP and SoC-FPGA
processor family processor type points of FFT 1-D FFT/ms SoC-FPGA 5CSEA5 1024 1.3124 4096 6.0449 ARM ARM Cortex-A8
with NEON1024 15.2585 4096 59.0241 DSP TMS320C6713 1024 12.9487 4096 51.7513 
下载: 导出CSV
-
-
点击查看大图
图(7) / 表(1)
计量
- 文章访问数: 5792
- HTML全文浏览量: 3344
- PDF下载量: 280
- 被引次数: 0
