网站地图
下载:
-
电磁诱导透明(electromagnetic induced transparency, EIT)是在激光驱动的原子系统中因不同途径的量子能级之间的相消干涉，使得吸收光谱内形成一个狭窄的透明窗口的现象[1-2]。EIT现象可以应用在许多地方，包括非线性器件、慢光器件、光开关、脉冲延迟和光学信息处理的存储[3-8]。然而，要产生EIT现象的条件极为严苛：极低温的环境；高强度的激光器制作三能级系统；工作频段狭窄，主要集中在可见光或附近区域[9]。
近年来，一种被称作等离子诱导透明(plasmon induced transparency, PIT)的类EIT现象在耦合谐振器[10-11]、电路模型[12]以及等离子结构[13-17]已经得到理论和实验证实，PIT现象的工作频段可从微波到可见光。PIT现象在超材料中可以通过不同谐振模式之间相消干涉获得[18]。当前最典型的获得PIT现象的方式是通过亮模式和暗模式两类本征模之间的干涉作用实现的，其中亮模式谐振器能与入射电磁场直接耦合，暗模式谐振器不能与外界电磁场耦合[19]。然而，基于超材料PIT现象的最大难点是获得较宽的透射窗口，较宽的透射窗口可以使得PIT效应的应用更加广泛。
本文中提出了一种双层可调谐的超材料结构，与一般的单层PIT结构不同，该结构可以使亮模式谐振器的移动空间更大，而且可以得到一个较宽的透射窗口，并且可以通过改变两个谐振器之间的距离改变透射窗口的位置。本文中首先对提出的结构进行仿真，然后对其透过率谱、电场图和电流图进行分析，最后通过构建相关数学模型对PIT现象进行解释，将仿真结果与理论结果很好地拟合在一起。
-
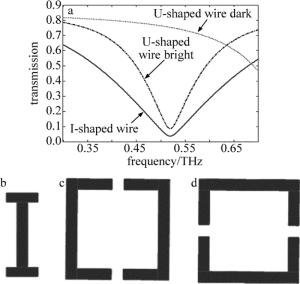
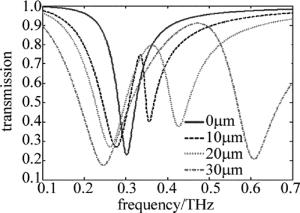
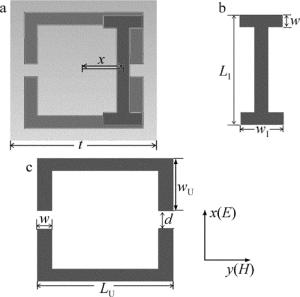
本文中所提出的双层结构如图 1a所示。上层为一个I形金属棒，下层为一对沿y轴对称的U形环，该谐振器是由这两种谐振单元在x, y方向上呈周期性排列而成的。太赫兹波垂直入射该结构，电场方向与x轴平行，磁场方向与y轴平行。该结构所用的金属为铝，电导率为3.72×107S/m，厚度为200nm。在两层超材料的之间为一层有损耗的聚酰亚胺(polyimide, PI)，介电常数εPI=2.96+i0.27。该结构的衬底为50μm厚的硅，介电常数εSi=11.56。偏移量x为I形金属棒到结构平面中心的距离，当I形金属棒位于该结构中心时，定义x=0μm；当I形金属棒随y轴正方向移动时，x的值也将随之增大。t为该结构的单元周期，其中t=120μm。I形金属棒和U形环的参量分别如图 1b、图 1c所示。其中I形金属棒的长度LI=86μm和宽度wI=30μm; U形环的长度LU=91μm和宽度wU=41μm，两个U形环之间的最短距离d=10μm，金属的线宽w=10μm。
Figure 1. Sketch of PIT structure
-
通常，为了实现PIT效应，需要亮模式和暗模式的谐振频率基本一致。由图 1可知，电场方向平行于I形金属棒，因此本结构的亮模式谐振器是I型金属棒，暗模式谐振器是U形环。通过CST STUDIO SUITE对该结构进行仿真。图 2a为仿真的亮、暗模式透过率谱，当把U形环调至亮模式时(结构如图 2c所示)，它的谐振频率与I形金属棒(结构如图 2b所示)一样，都为0.519THz，为了实现PIT效应，需要将U形环调至暗模式(结构如图 2d所示)，该结构在透过率谱内并不存在谐振峰。
Figure 2. Transmittance spectrum of light and dark mode and their structures
由图 3可知，在外界太赫兹波入射下，I形金属棒和U形环发生了极化，正负电荷分别集聚在一侧，电流也只存在一个方向，因此在0.519THz时，I形金属棒和U形环都发生了偶极谐振。其中，图 3a、图 3b中的电场强度范围为-10.8×105 V/m~10.8×106V/m；图 3c、图 3d中的电流强度范围为0A/m~16070A/m。
Figure 3. Electric field and current distribution of bright and dark resonators at 0.519THz
对整个PIT结构进行仿真，得到的仿真结果图 4所示。在不改变聚酰亚胺厚度的情况下，当x=0μm时，透过率谱上只在0.305THz处出现了一个谐振峰。当x增大时，透过率谱上出现两个谐振峰，开始出现PIT现象。当x=10μm时，PIT窗口的半峰全宽仅为0.044THz。随着x值的增大，低谐振峰的谐振频率和幅值改变很小，而高谐振峰的谐振频率发生蓝移且幅值不断增大。因此，随着x值的增大，将形成一个宽带PIT窗口。到了x=30μm时，出现了一个半峰全宽为0.276THz的PIT窗口。
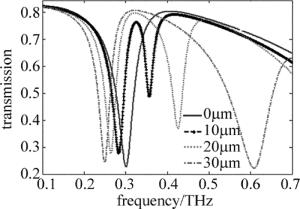
Figure 4. Relationship between transmission and frequency of PIT structure with different x when the thickness of polyimide layer is 10μm
单层结构的PIT窗口的频率与亮模式谐振器的谐振频率一般都是相同的。与一般的PIT单层结构不同的是，该结构PIT窗口的频率为0.326THz，而亮模式谐振器的谐振频率为0.519THz，所以双层结构的PIT窗口的频率与亮模式谐振器的谐振频率不同。通过仿真可知，只改变聚酰亚胺层的厚度即亮、暗模式谐振器之间的垂直距离可以移动PIT窗口的频率。如图 5所示，当聚酰亚胺厚度为10μm时，PIT窗口的频率为0.326THz，半峰全宽为0.135THz。当两个谐振器的垂直距离不断增大时，PIT透过率谱和PIT窗口的频率不断蓝移。当聚酰亚胺厚度到了50μm时，PIT窗口的频率为0.448THz，半峰全宽为0.232THz。虽然透射窗口的宽度不断加宽，但是由于有损耗的聚酰亚胺层不断加厚使得谐振频率的幅值越来越小，因此PIT现象并没有因为PIT窗口的加宽而变得明显。
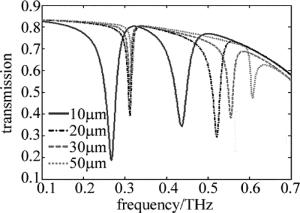
Figure 5. Relationship between transmission and frequency with different thicknesses of polyimide layer when x=20μm
在x=0μm时(结构如图 6a所示)，只存在一个谐振频率0.305THz。当太赫兹波垂直平面入射时，I此处形金属棒能直接与外界电磁波耦合。由于该结构在x-O-z平面中是对称的，因此由I形金属棒产生的电磁场对U形环左右两边产生的作用是相同的，由此产生相同方向的电流会发生抵消，根据仿真结果(见图 6b)，此时主要是由I形金属棒引起的偶极谐振，U形环此时也发生了较弱的偶极谐振。所以当频移时，并不会改变U形环的谐振方式，因此x=0μm时，只存在一个谐振峰。当x增大时，该结构在x-O-z平面是不对称的。如图 6d所示，当x=20μm时(结构如图 6c所示)，由于结构的不对称，由I形金属棒产生的电磁场对U形环左右两边产生的作用不同，因此在PIT窗口的频率内，由于右边产生的电流被左边抵消，所以左边所产生的电流密度比右边的大，此时U形环内形成了电流环路，因此U形环发生了LC谐振。由于能量的转移到了U形环上，因此I形金属棒与外界的耦合被抑制，此时I形金属棒上的电流密度很小。随着x值的增大，该结构的不对称性越来越显著，左右两边的电流密度差距将逐渐增大，明、暗模式之间的相消干涉将越发明显，因此导致了PIT窗口的加宽。如图 6b中的电流强度范围为0A/m~32936A/m, 如图 6d中的电流强度范围为0A/m~16138A/m。
Figure 6. PIT structure and current distribution when the thickness of polyimide layer is 10μm
-
与EIT三能级系统相似，PIT模型一般也存在一个基态|0〉和两个激发态|1〉和|2〉。允许跃迁|0〉→|1〉和禁止跃迁|0〉→|2〉分别对应的是亮模式谐振和在暗模式谐振。激发态|1〉和|2〉之间的过渡对应的是亮暗模式之间的耦合，该耦合会引起一个通过|0〉→|1〉和|0〉→|1〉→|2〉→|1〉途径的干涉相消，从而导致在狭窄的频带内形成一个PIT窗口。在PIT超材料中，这种干涉可以用洛伦兹线型模型表示为[20]：
$ \begin{align} &p\prime\prime \left( t \right){{\omega }_{\text{b}}}^{-2}+{{\gamma }_{1}}p\prime \left( t \right){{\omega }_{\text{b}}}^{-1}+p\left( t \right)= \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ f\left( t \right)-\kappa q(t) \\ \end{align} $
(1) $ q\prime\prime \left( t \right){{\omega }_{\text{d}}}^{-2}+{{\gamma }_{2}}q\prime \left( t \right){{\omega }_{\text{d}}}^{-1}+q\left( t \right)=-\kappa q(t)~ $
(2) 式中，ωb为亮模式的谐振频率，γ1为亮模式阻尼率，ωd为暗模式的谐振频率，γ2为暗模式阻尼率，f(t)代表外界场的强度，p(t)代表亮模式激励源的强度，q(t)为暗模式激励源的强度; 亮模式的谐振频率ωb和阻尼率γ1是由外界场f(t)以及激励源p(t)所控制的，而暗模式的谐振频率ωd和阻尼率γ2是由激励源q(t)所控制的，且满足|ωd－ωb|=ωb; κ是两种谐振器之间的谐振系数。(1)式和(2)式可以在频域中由$ p\left( t \right)=\tilde{p}\left( \omega \right){{\text{e}}^{-\text{i}\omega t}}$和$q\left( t \right)=\tilde{q}\left( \omega \right){{\text{e}}^{-\text{i}\omega t}} $来表达：
$ \tilde p\left( \omega \right) = \frac{{{D_{\rm{d}}}\left( \omega \right)\tilde f\left( \omega \right)}}{{{D_{\rm{d}}}\left( \omega \right){D_{\rm{b}}}\left( \omega \right) - {\kappa ^2}}} $
(3) $ \tilde q\left( \omega \right) = \frac{{\kappa \tilde f\left( \omega \right)}}{{{D_{\rm{d}}}\left( \omega \right){D_{\rm{b}}}\left( \omega \right) - {\kappa ^2}}} $
(4) 其中：
$ {D_{\rm{b}}}\left( \omega \right) = 1 - {\left( {\frac{\omega }{{{\omega _{\rm{b}}}}}} \right)^2} - {\rm{i}}{\gamma _1}\left( {\frac{\omega }{{{\omega _{\rm{b}}}}}} \right){\rm{ }} $
(5) $ {D_{\rm{d}}}\left( \omega \right) = 1 - {\left( {\frac{\omega }{{{\omega _{\rm{d}}}}}} \right)^2} - {\rm{i}}{\gamma _2}\left( {\frac{\omega }{{{\omega _{\rm{d}}}}}} \right){\rm{ }} $
(6) 式中，ω代表当前频率，是因变量，随着ω的变化，接下来一系列参量也会随之变化。$ \tilde{f}\left( \omega \right)$代表了外界场f(t)经过傅里叶变换由时域变为频域、由频率ω影响的变量。
如果超材料的厚度比入射波长小得多，就可以用磁导率χ来描述外部辐射的响应。由于在该结构中铝的厚度仅为200nm，因此磁导率和透过率可分别表达为：
$ \chi \approx \frac{{\tilde p\left( \omega \right)\beta }}{{\tilde f\left( \omega \right)}} = \frac{{\beta {D_{\rm{d}}}\left( \omega \right)}}{{{D_{\rm{d}}}\left( \omega \right){D_{\rm{b}}}\left( \omega \right) - {\kappa ^2}}} $
(7) $ \left| {\tilde t} \right| = \left| {\frac{{c\left( {1 + n} \right)}}{{c\left( {1 + n} \right) - {\rm{i}}\omega \chi }}} \right| $
(8) 式中，β为静态表面电导率，${\tilde{t}} $为结构的透过率，c为光速，n为衬底的折射率。
由(8)式可以得到该数值模型在I形金属棒不断移动时的透过率谱。由于对该数值模型进行讨论时，对衬底的损耗忽略不计，所以图 7中所得的透过率会比仿真的透过率大。与仿真结果一样，当x=0μm时，透过率谱上只出现了一个谐振峰，此时耦合系数κ很小，代表明、暗模式之间耦合较弱。随着x值的增大，明、暗模式谐振器的耦合系数κ也会随之增大，使得PIT窗口不断加宽。
Figure 7. Relationship between transmission and frequency of numerical model with different x when the thickness of polyimide layer is 10μm
-
本文中提出了一种新型双层宽带PIT结构。PIT窗口的宽度是通过移动I形金属棒的位置来控制的。当I型金属棒位于该结构中心时，并未出现PIT现象; 当I形金属棒向左右移动时，由于结构的不对称性，会出现PIT窗口。当结构的不对称越大，PIT窗口的带宽也就越大。与一般的PIT单层结构不同的是，双层PIT结构的透射窗口频率可以与亮模式谐振器不同，PIT窗口的频率可以通过改变聚酰亚胺层厚度即亮、暗模式谐振器之间的距离调节。用洛伦兹线型模型同样可以对该结构进行数学模型的分析，数学模型分析的结果基本与仿真相符。衬底的损耗也会对谐振峰的幅值和带宽有较大的影响。该结构为设计宽带PIT结构提供了一个很好的思路。
可调谐太赫兹等离子诱导透明的研究
Study on transparency structure induced by tunable terahertz plasmon
-
摘要: 为了获得一个较宽的等离子诱导透明（PIT）窗口，提出了一种双层可调谐的太赫兹超材料结构。采用仿真方法对该结构的透过率谱、电场图和电流图进行了分析，并通过数学模型分析了透射窗口形成机理。结果表明，该结构可以使亮模式谐振器的移动空间更大，而且可以得到一个较宽的透射窗口；该结构能通过平移I形金属棒的位置进而控制PIT窗口的宽度。仿真结果与理论结果拟合得很好。Abstract: In order to obtain a wider plasma induced transparency (PIT) window, a dual layer tunable terahertz metamaterial structure was proposed. The transmission spectrum, electric field diagram and current diagram of the structure were simulated and analyzed. The formation mechanism of transmission window was analyzed by a mathematical model. The results show that the structure makes the move space of light-mode resonator wider and a wider transmission window can be obtained. The structure can change the width of PIT window by moving the position of I-shaped metal bar. The simulation results are well fitted with the theoretical results.
-
Figure 1. Sketch of PIT structure
a—unit structure of PIT b—structure of I-shaped wire c—structure of U-shaped rings
Figure 2. Transmittance spectrum of light and dark mode and their structures
a—transmittance spectrum of light and dark mode b—structure of bright mode c—structure of U-shaped rings as bright mode d—structure of U-shaped rings as dark mode
Figure 3. Electric field and current distribution of bright and dark resonators at 0.519THz
a—electric field distribution of I-shaped wire b—electric field distribution of U-shaped rings c—current distribution of I-shaped wired—current distribution of U-shaped rings
Figure 4. Relationship between transmission and frequency of PIT structure with different x when the thickness of polyimide layer is 10μm
Figure 5. Relationship between transmission and frequency with different thicknesses of polyimide layer when x=20μm
Figure 6. PIT structure and current distribution when the thickness of polyimide layer is 10μm
a—PIT structure with x=0μm b—electric field distribution with x=0μm, frequency of 0.305THz, and current intensity of 0A/m~32936A/m c—PIT structure with x=20μm d—electric field distribution with x=20μm, frequency of 0.326THz, and current intensity of 0A/m~16138A/m
-
[1] FLEISCHHAUER M, PHYSIK F. Electromagnetically induced transparency:Optics in coherent media[J]. Reviews of Modern Physics, 2005, 77(2):633-673. doi: 10.1103/RevModPhys.77.633 [2] YANG L J, ZHANG L Sh, LI X L, et al. The study of the electromagnetic induced transparency in multi-window tunable[J]. Journal of Physics, 2006, 55(10):5206-5210(in Chinese). [3] MONAT C, de STERKE M, EGGLETON B J. Slow light enhanced nonlinear optics in periodic structures[J]. Journal of Optics, 2010, 12(10):104003. doi: 10.1088/2040-8978/12/10/104003 [4] BOYD R W. Material slow light and structural slow light:similarities and differences for nonlinear optics [Invited] [J]. Journal of the Optical Society of America, 2011, B28(12):A38-A44. [5] KRAUSS T F. Why do we need slow light?[J]. Nature Photonics, 2008, 2(8):448-450. doi: 10.1038/nphoton.2008.139 [6] PHILLIPS D F, FLEISCHHAUER A, MAIR A, et al. Storage of light in atomic vapor[J]. Physical Review Letters, 2000, 86(5):783-786. [7] CHEN H T, O'HARA J F, AZAD A K, et al. Manipulation of terahertz radiation using metamaterials[J]. Laser & Photonics Reviews, 2011, 5(4):513-533. [8] WAN M, SONG Y, ZHANG L, et al. Broadband plasmon-induced transparency in terahertz metamaterials via constructive interference of electric and magnetic couplings[J]. Optics Express, 2015, 23(21):27361-27368. doi: 10.1364/OE.23.027361 [9] ZHU Z, YANG X, GU J, et al. Broadband plasmon induced transparency in terahertz metamaterials[J]. Nanotechnology, 2013, 24(21):214003. doi: 10.1088/0957-4484/24/21/214003 [10] YANG X, YU M, KWONG D L, et al. All-optical analog to electromagnetically induced `transparency in multiple coupled photonic crystal cavities[J]. Physical Review Letters, 2009, 102(17):173902. doi: 10.1103/PhysRevLett.102.173902 [11] XU Q, SANDHU S, POVINELLI M L, et al. Experimental realization of an on-chip all-optical analogue to electromagnetically induced transparency[C]//Lasers and Electro-Optics, 2006 and 2006 Quantum Electronics and Laser Science Conference. New York, USA: IEEE, 2006: 1-2. [12] ALZAR C L G, MARTINEZ M A G, NUSSENZVEIG P. Classical analog of electromagnetically induced transparency[J]. American Journal of Physics, 2001, 70(1):37-41. [13] SINGH R, AL-NAIB I A I, YANG Y, et al. Observing metamaterial induced transparency in individual Fano resonators with broken symmetry[J]. Applied Physics Letters, 2011, 99(20):201107. doi: 10.1063/1.3659494 [14] PARVINNEZHAD H M, PHILIP E, RIVERA E, et al. Plasmon-induced transparency by hybridizing concentric-twisted double split ring resonators[J]. Scientific Reports, 2015, 5(1):15735. doi: 10.1038/srep15735 [15] BAI Y, CHEN K, LIU H, et al. Optically controllable terahertz modulator based on electromagnetically-induced-transparency-like effect[J]. Optics Communications, 2015, 353:83-89. doi: 10.1016/j.optcom.2015.05.005 [16] CHEN X, FAN W H. Plasmon-induced transparency in terahertz planar metamaterials[J]. Optics Communications, 2015, 356:84-89. doi: 10.1016/j.optcom.2015.07.063 [17] HAN J, GU J, TIAN Z, et al. Plasmon-induced transparency in terahertz metamaterials[C]//International Conference on Infrared, Millimeter, and Terahertz Waves. New York, USA: IEEE, 2012: 1-2. [18] TAUBERT R, HENTSCHEL M, KÄSTEL J, et al. Classical analog of electromagnetically induced absorption in plasmonics[J]. Nano Letters, 2012, 12(3):1367-1371. doi: 10.1021/nl2039748 [19] LIU N, LANGGUTH L, WEISS T, et al. Plasmonic analogue of electromagnetically induced transparency at the Drude damping limit[J]. Nature Materials, 2009, 8(9):758-762. doi: 10.1038/nmat2495 [20] TASSIN P, ZHANG L, ZHAO R, et al. Electromagnetically induced transparency and absorption in metamaterials:the radiating two-oscillator model and its experimental confirmation[J]. Physical Review Letters, 2012, 109(18):187401. doi: 10.1103/PhysRevLett.109.187401 -
点击查看大图
计量
- 文章访问数: 5173
- HTML全文浏览量: 3217
- PDF下载量: 199
- 被引次数: 0
