-
利用地面3维激光扫描仪进行扫描作业时,若遇扫描范围过大或扫描视角被其它物体遮挡等情况,应增加测站来完成全部扫描。即在扫描之前将3个或3个以上的球标靶(白球)合理布设至被扫描物体周围,之后利用球标靶的球心坐标通过刚体变换公式实现坐标转换,将所有扫描数据统一至同一坐标系下,为后期数据处理提供完整的研究对象点云坐标数据。其中,球标靶球心坐标通过球面拟合得到,因此,球面拟合精度直接影响到球心坐标精度,进而对整个坐标转换精度及之后数据处理、数据分析、数据建模的精度产生极大影响。
传统最小二乘(least squares,LS)法[1]、总体最小二乘(total least squares,TLS)法[2-3]等球面拟合方法在拟合过程中,均将点云各点当做等独立精度观测值处理,由于受观测环境、系统误差等因素影响,地面3维激光扫描获取的空间3维坐标x, y, z这3个方向上均含有误差且各点点位精度均不相同,若采用上述方法对球面点云数据进行拟合,所得参量解并非球面参量的最或然值。作者在总体最小二乘法的基础上引入加权总体最小二乘(weighted total least squares,WTLS)模型[4-11],结合权函数中国科学院大地测量与地球物理研究所(Institute of Geodesy and Geophysics, IGG)Ⅲ方案[12-13],新的加权总体最小二乘点云球面拟合算法(weighted total least squares combined with IGGⅢ scheme,IGGⅢ-WTLS),其通过对系数矩阵及观测向量的权阵进行合理定义及设计,在参量迭代解算过程中根据IGGⅢ方案确定的点位精度,自适应地对拟合权阵进行修正,提高拟合精度。
-
加权总体最小二乘球面拟合的变量误差(error-in-variables, EIV)模型为:
$ \mathit{\boldsymbol{Y}} - {\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{Y}}} = \left( {\mathit{\boldsymbol{A}} - {\mathit{\boldsymbol{E}}_\mathit{\boldsymbol{A}}}} \right) \cdot \mathit{\boldsymbol{X}} $
(1) 式中,Y为含偶然误差eY的n×1维观测向量,A为含偶然误差EA的n×4维系数矩阵,X为待求球面参量:
$ \begin{array}{*{20}{c}} {\mathop {\mathit{\boldsymbol{Y}}}\limits_{n \times 1} = \left[ {\begin{array}{*{20}{c}} {x_1^2 + y_1^2 + z_1^2}\\ {x_2^2 + y_2^2 + z_2^2}\\ \vdots \\ {x_n^2 + y_n^2 + z_n^2} \end{array}} \right],\mathop {\mathit{\boldsymbol{A}}}\limits_{n \times 4} = \left[ {\begin{array}{*{20}{c}} {2{x_1}}&{2{y_1}}&{2{z_1}}&1\\ {2{x_2}}&{2{y_2}}&{2{z_2}}&1\\ \vdots&\vdots&\vdots&\vdots \\ {2{x_n}}&{2{y_n}}&{2{y_n}}&1 \end{array}} \right],\mathop {\mathit{\boldsymbol{X}}}\limits_{4 \times 1} = \left[ {\begin{array}{*{20}{c}} a\\ b\\ c\\ {{r^2} - {a^2} - {b^2} - {c^2}} \end{array}} \right],}\\ {\mathop {{\mathit{\boldsymbol{E}}_A}}\limits_{n \times 4} = \left[ {\begin{array}{*{20}{c}} {{v_{{x_1}}}}&{{v_{{y_1}}}}&{{v_{{z_1}}}}&1\\ {{v_{{x_2}}}}&{{v_{{y_2}}}}&{{v_{{z_2}}}}&1\\ \vdots&\vdots&\vdots&\vdots \\ {{v_{{x_n}}}}&{{v_{{y_n}}}}&{{v_{{z_n}}}}&1 \end{array}} \right],\mathop {{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{Y}}}}\limits_{n \times 3} = \left[ {\begin{array}{*{20}{c}} {2\left( {{x_1}{v_{{x_1}}} + {y_1}{v_{{y_1}}} + {z_1}{v_{{z_1}}}} \right)}\\ {2\left( {{x_2}{v_{{x_2}}} + {y_2}{v_{{y_2}}} + {z_2}{v_{{z_2}}}} \right)}\\ \vdots \\ {2\left( {{x_n}{v_{{x_n}}} + {y_n}{v_{{y_n}}} + {z_n}{v_{{z_n}}}} \right)} \end{array}} \right]} \end{array} $
(2) 式中,eY舍去了$ \left( {{v_{{x_i}}}^2, {v_{{y_i}}}^2, {v_{{z_i}}}^2} \right)(i = 1, 2, \ldots , n)$等极小的二次项。
随机误差eY与EA的统计性质如下:
$ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{Y}}}}\\ {{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{A}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{Y}}}}\\ {{\rm{vec}}\left( {{\mathit{\boldsymbol{E}}_\mathit{\boldsymbol{A}}}} \right)} \end{array}} \right] $
(3) (3) 式服从的正态分布。式中,vec()为矩阵拉直变换,σ02为未知方差分量; QY, QA为eY与eA的对称、非奇异协因数阵,且有:
$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{Y}}} = \mathit{\boldsymbol{P}}_\mathit{\boldsymbol{Y}}^{ - 1}\\ {\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{X}}} = \mathit{\boldsymbol{P}}_\mathit{\boldsymbol{X}}^{ - 1}\\ {\mathit{\boldsymbol{Q}}_0} = \mathit{\boldsymbol{P}}_0^{ - 1}\\ {\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{A}}} = {\mathit{\boldsymbol{Q}}_0} \otimes {\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{X}}} = \mathit{\boldsymbol{P}}_\mathit{\boldsymbol{A}}^{ - 1} \end{array} \right. $
(4) 式中,PY为观测值权阵,PA为系数矩阵A的权阵,PX和P0分别为系数矩阵A的行向量权阵及列向量矩阵,“ $ \otimes $ ”为Kronecker积。
加权总体最小二乘的参量估计准则为:
$ {\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{Y}}}^{\rm{T}}{\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{Y}}}{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{Y}}} + {\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{A}}}^{\rm{T}}{\mathit{\boldsymbol{P}}_0} \otimes {\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{X}}}{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{A}}} = \min $
(5) -
根据加权总体最小二乘球面拟合EIV模型,令:
$ \left\{ \begin{array}{l} u = 2x\\ w = {x^2} + {y^2} + {z^2} \end{array} \right. $
(6) 由于x, y, z独立等精度,则有:
$ \left\{ \begin{array}{l} {\sigma _u} = {\sigma _{2x}} = {\sigma _{2y}} = {\sigma _{2z}}\\ {\sigma _x} = {\sigma _y} = {\sigma _z}\\ {\sigma _w} = {\sigma _{{x^2} + {y^2} + {z^2}}} \end{array} \right. $
(7) 式中,${\sigma _x}, {\sigma _y}, {\sigma _z}, {\sigma _u}, {\sigma _w} $分别为$ x, y, z, u, w$的方差。
由协因素传播定律得:
$ \sigma _u^2 = 4\sigma _x^2 = 4\sigma _y^2 = 4\sigma _z^2 $
(8) $ \begin{array}{*{20}{c}} {\sigma _w^2 = {{\left( {\frac{{{\rm{d}}w}}{{{\rm{d}}x}}} \right)}^2} + {{\left( {\frac{{{\rm{d}}w}}{{{\rm{d}}y}}} \right)}^2} + {{\left( {\frac{{{\rm{d}}w}}{{{\rm{d}}z}}} \right)}^2} = }\\ {4{x^2}\sigma _x^2 + 4{y^2}\sigma _y^2 + 4{z^2}\sigma _z^2 = }\\ {4\left( {{x^2} + {y^2} + {z^2}} \right)\sigma _x^2} \end{array} $
(9) 令单位权方差σ02=1,则有:
$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{Q}}_u} = \sigma _u^2/\sigma _0^2 = 4\sigma _x^2\\ {\mathit{\boldsymbol{Q}}_w} = \sigma _w^2/\sigma _0^2 = 4\left( {{x^2} + {y^2} + {z^2}} \right)\sigma _x^2 \end{array} \right. $
(10) 式中,Qu, Qw分别为u, w的协方差阵。
由(10)式可得:
$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{Q}}_w} = \left( {{x^2} + {y^2} + {z^2}} \right){\mathit{\boldsymbol{Q}}_u} = w{\mathit{\boldsymbol{Q}}_u}\\ {\mathit{\boldsymbol{P}}_w} = {\mathit{\boldsymbol{P}}_u}/w \end{array} \right. $
(11) 式中,Pw为EIV模型的观测向量权阵, 即PY;Pu为系数矩阵的行向量矩阵, 即PX。
根据(11)式定义系数矩阵A的列向量权阵P0、行向量矩阵初始权阵PX、观测向量Y的初始权阵PY如下:
$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{P}}_0} = {\rm{diag}}\left( {1,1,1,0} \right)\\ {\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{X}}} = {\rm{diag}}\left( {{\mathit{\boldsymbol{P}}_{{\mathit{\boldsymbol{X}}_1}}},{\mathit{\boldsymbol{P}}_{{\mathit{\boldsymbol{X}}_2}}}, \cdots ,{\mathit{\boldsymbol{P}}_{{\mathit{\boldsymbol{X}}_n}}}} \right)\\ {\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{Y}}} = {\rm{diag}}\left( {{\mathit{\boldsymbol{P}}_{{\mathit{\boldsymbol{Y}}_1}}},{\mathit{\boldsymbol{P}}_{{\mathit{\boldsymbol{Y}}_2}}}, \cdots ,{\mathit{\boldsymbol{P}}_{{\mathit{\boldsymbol{Y}}_n}}}} \right) \end{array} \right. $
(12) 式中,$ {\mathit{\boldsymbol{P}}_{{\mathit{\boldsymbol{Y}}_i}}} = {\mathit{\boldsymbol{P}}_{{\mathit{\boldsymbol{X}}_i}}}/\left( {{x_i}^2 + {y_i}^2 + {z_i}^2} \right)(i = 1, 2, \ldots , n)$。
-
由于点云数据受环境影响大,粗差点较多,顾及IGGⅢ方案在测绘领域较好的适用性[14-15],选取IGGⅢ方案对点云参量迭代解算过程中的拟合权阵(A的行向量矩阵的初始权阵PX、观测向量Y的初始权阵PY,且有$ \mathit{\boldsymbol{\bar P}} = \mathit{\boldsymbol{P\omega }}$ [13],P为PX, PY总称, $ {\mathit{\boldsymbol{\bar P}}}$为修正后权值,ω为权因子)进行修正,其权因子计算公式为:
$ {\omega _i} = \left\{ \begin{array}{l} 1,\left( {\left| {{V_i}/\sigma } \right| < {k_0}} \right)\\ \frac{{{k_0}}}{{\left| {{V_i}/\sigma } \right|}}\left( {\frac{{{k_1} - \left| {{V_i}/\sigma } \right|}}{{{k_1} - {k_0}}}} \right),\left( {{k_0} \le \left| {{V_i}/\sigma } \right| < {k_1}} \right)\\ 0,\left( {\left| {{V_i}/\sigma } \right| > {k_1}} \right) \end{array} \right. $
(13) 式中,Vi为残差,σ为中误差,k0和k1为调节权因子的阈值。根据中误差分布概率理论[13],一般有:k0=1.0~1.5,k1=2.5~3.0。本文中令Vi=di,di为点M(xi, yi, zi)到拟合模型表面的距离(见(14)式),根据IGG Ⅲ方案在测绘领域的适用性研究[12-13, 16],令k0=1.5, k1=2.5,即认为当观测值Vi < 1.5σ时,则可认为该点不含误差,其权因子ωi不变; 当Vi>2.5σ时,则可认为该观测值为粗差,予以剔除。
$ \begin{array}{*{20}{c}} {{d_i} = }\\ {\left| {\sqrt {{{\left( {{x_i} - a} \right)}^2} + {{\left( {{y_i} - b} \right)}^2} + {{\left( {{z_i} - c} \right)}^2}} - r} \right|} \end{array} $
(14) 式中,$ a, b, c, r$为球面参量。
-
在加权总体最小二乘模型的基础上,通过合理定义权阵,结合1.3节中所定义的权函数IGGⅢ方案提出了新的加权总体最小二乘点云球面拟合算法(IGGⅢ-WTLS法),根据(5)式所示的参量估计准则,定义算法的具体思路及模型解算步骤如下。
(1) 利用LS法求得拟合模型参量估值,之后根据1.2节中所述方法定义系数矩阵A的列向量权阵P0及其行向量初始权阵PX(1)、观测向量初始权阵PY(1)(上标加括号表示迭代)。
(2) 求取参量$ \mathit{\boldsymbol{X}} = {\left[ {a, b, c, {r^2} - {a^2} - {b^2} - {c^2}} \right]^{\rm{T}}}$的迭代初始值:
$ \left\{ \begin{array}{l} {{\hat v}^{\left( 0 \right)}} = 0\\ {{\hat X}^{\left( 0 \right)}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{Y}}}^{\left( 1 \right)}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{Y}}}^{\left( 1 \right)}\mathit{\boldsymbol{Y}}\\ {{\hat \mu }^{\left( 0 \right)}} = {\left\{ {{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{Y}}}^{\left( 1 \right)} + \left[ {{{\left( {{{\hat X}^{\left( 0 \right)}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{Q}}_0}{{\hat X}^{\left( 0 \right)}}} \right]{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{X}}}^{\left( 1 \right)}} \right\}^{ - 1}}\\ {{\hat X}^{\left( 1 \right)}} = \left[ {{{\left( {{{\hat \mu }^{\left( 0 \right)}}\mathit{\boldsymbol{A}}} \right)}^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}{{\hat \mu }^{\left( 0 \right)}}} \right]\mathit{\boldsymbol{Y}} \end{array} \right. $
(15) 式中,Q0为P0的广义逆。
(3) 计算$ {{\hat \mu }^{(i)}}, {{\hat \lambda }^{(i)}}$及$ {{\hat v}^{(i)}}$:
$ \left\{ \begin{array}{l} {{\hat \mu }^{\left( i \right)}} = {\left\{ {{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{Y}}}^{\left( i \right)} + \left[ {{{\left( {{{\hat X}^{\left( i \right)}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{Q}}_0}{{\hat X}^{\left( i \right)}}} \right]{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{X}}}^{\left( i \right)}} \right\}^{ - 1}}\\ {{\hat \lambda }^{\left( i \right)}} = {{\hat \mu }^{\left( i \right)}} \cdot \left( {\mathit{\boldsymbol{Y}} - \mathit{\boldsymbol{A}}{{\hat X}^{\left( i \right)}}} \right)\\ {{\hat v}^{\left( i \right)}} = {\left( {{{\hat \lambda }^{\left( i \right)}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{X}}}^{\left( i \right)}{{\hat \lambda }^{\left( i \right)}} \end{array} \right. $
(16) (4) 计算$ {{\hat X}^{\left( {i + 1} \right)}}$:
$ {{\hat X}^{\left( {i + 1} \right)}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}{{\hat \mu }^{\left( i \right)}}\mathit{\boldsymbol{A}} - {{\hat v}^{\left( i \right)}} \cdot {\mathit{\boldsymbol{Q}}_0}} \right)^{ - 1}} \cdot \left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}{{\hat \mu }^{\left( i \right)}}\mathit{\boldsymbol{Y}}} \right) $
(17) (5) 利用(14)式各点到拟合模型表面的距离。
(6) 根据(13)式计算权因子ω(i),令$ {\mathit{\boldsymbol{P}}^{(i + 1)}} = {\mathit{\boldsymbol{P}}^{\left( i \right)}}{\omega ^{(i)}}$,之后根据权阵定义准则重新设定权阵$ {\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{X}}}^{(i + 1)}, {\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{Y}}}^{(i + 1)}$。
(7) 重复步骤(3)~步骤(6),直到$\parallel {{\hat X}^{(i + 1)}} - {{\hat X}^{(i)}}\parallel < {\delta _0}({\delta _0}$为给定阈值,本文中取为10-6)。
(8) 计算单位权重中误差${{\hat \sigma }_0} $及球面拟合精度${{\hat \sigma }_{\rm{s}}} $,进行精度评定:
$ \left\{ \begin{array}{l} {{\hat \sigma }_0} = \sqrt {\frac{{{{\left( {{\lambda ^{\left( i \right)}}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{Y}} - \mathit{\boldsymbol{A}}\hat X} \right)}}{{n - t}}} \\ {{\hat \sigma }_{\rm{s}}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {d_i^2} } \end{array} \right. $
(18) -
为了对本文中所构建球面拟合方法的适用性及优越性进行验证,分别利用其对模拟球面数据、实际扫描球面数据进行拟合。
-
对于球面方程:
$ {\left( {x - 10} \right)^2} + {\left( {y - 10} \right)^2} + {\left( {z - 1} \right)^2} = 200 $
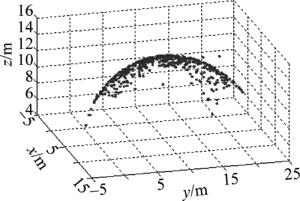
(19) 其坐标球心为(10, 10, 1),半径为$ 10\sqrt 2 $ m,利用MATLAB在x, y∈[0, 20]范围内随机生成500个点,并将第12, 第15, 第53, 第67和第465号点替换成粗差点,如图 1所示。
分别利用LS法、TLS法、IGGⅢ-WTLS法对不含粗差、加入随机粗差的两组球面点云数据进行拟合,结果如表 1和表 2所示。
Table 1. Fitting precision without gross errors
methods Δ|a|/m Δ|b|/m Δ|c|/m Δ|r|/m $ {{\hat \sigma }_0}$ /m ${{\hat \sigma }_{\rm{s}}} $ /m LS method 0.0002 0 0.0016 0.0014 0.08004 0.00282 TLS method 0.0002 0 0.0015 0.0014 0.08004 0.00282 IGGⅢ-WTLS method 0.0005 0 0 0.0008 0.00112 0.00285 Table 2. Fitting precision with gross errors
methods Δ|a|/m Δ|b|/m Δ|c|/m Δ|r|/m $ {{\hat \sigma }_0}$ /m ${{\hat \sigma }_{\rm{s}}} $ /m LS method 0.0670 0.0285 0.1754 0.2409 5.21910 0.20223 TLS method 3.5674 0.9320 11.1511 7.7432 34.33430 2.39240 IGGⅢ-WTLS method 0.0026 0.0008 0.0035 0.0717 0.00530 0.20114 表 1中,由于数据取位的原因,各方法所得参量与实际参量之间存在一定偏差,但各参量值非常接近实际参量值,单位拟合权重中误差与球面拟合精度较小,各方法拟合效果均比较好。其中,LS法忽视了系数矩阵误差,TLS法虽同时考虑了观测向量与系数矩阵误差,但未考虑各观测值的点位精度,以上两种算法的单位权重中误差$ {{\hat \sigma }_0}$均大于IGGⅢ-WTLS法,拟合效果相对较差。
由表 2可得,LS法受粗差影响,拟合效果明显下降;TLS法过多考虑到系数矩阵不含误差部分,拟合效果最差;IGGⅢ-WTLS法考虑了系数矩阵误差与观测向量误差的同时,根据点与拟合球面的相关关系,成功进行了粗差探测与合理权值替换,较好抵抗了粗差干扰,各项拟合指标均优于其它算法,拟合效果最好。
-
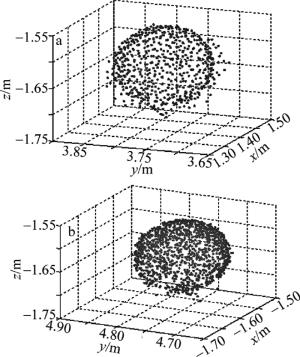
利用徕卡Scanstation C10地面3维激光扫描仪对真实场景进行扫描,获取实际球面点云数据(半径为0.0725m),如图 2所示。分别利用LS法、TLS法、IGGⅢ-WTLS法对两组球面点云数据进行拟合,拟合结果如表 3所示(表中,$ \hat a, \hat b, \hat c, \hat r$为球面参量$ a, b, c, r$的最或然值)。
Table 3. Real spherical parameters and fitting precision
samples methods $ {\hat a}$ /m ${\hat b} $ /m $ {\hat c}$ /m $ {\hat r}$ /m Δ|r|/m $ {{\hat \sigma }_0}$ /m $ {{\hat \sigma }_{\rm{s}}}$ /m spherical Ⅰ LS method 0.0099 5.8443 -1.6388 0.0735 0.0010 7.7080×10-5 5.0800×10-3 TLS method 0.0099 5.8443 -1.6388 0.0735 0.0010 7.7080×10-5 5.0800×10-3 IGGⅢ-WTLS method 0.0083 5.8454 -1.6357 0.0724 0.0001 1.0440×10-6 9.4506×10-4 spherical Ⅱ LS method 1.3982 3.7690 -1.6291 0.0736 0.0011 8.2813×10-4 5.4274×10-3 TLS method 1.3982 3.7691 -1.6291 0.0736 0.0011 8.2813×10-4 5.4278×10-3 IGGⅢ-WTLS method 1.3963 3.7694 -1.6247 0.0717 0.0008 1.0084×10-5 7.0619×10-4 由于实验中所用球面点云数据经过粗差剔除等处理,因此所含误差较少,由表 3可知,各算法所求参量较为接近,单位权重中误差、球面拟合精度较小,拟合效果较为理想。其中,由于数据纯度较高,因此LS法与TLS法计算结果基本一致,仅球2参量b相差了0.0001m;LS法、TLS法、IGGⅢ-WTLS法所得球标靶1半径r相对误差分别为1.38%, 1.38%, 0.14%,LS法、TLS法、IGGⅢ-WTLS法所得球标靶2半径r相对误差分别为1.52%, 1.52%, 1.10%,同时IGGⅢ-WTLS法两项精度评定指标均小于LS法及TLS法,因此,IGGⅢ-WTLS法拟合效果优于其它两种算法,所得参量解更可靠。
-
(1) 由于地面3维激光扫描点云各点精度不等,依据广义极大似然估计各权函数特点及其适用范围,选用IGGⅢ方案对加权总体最小二乘球面拟合算法进行改进,提出了IGGⅢ-WTLS点云拟合算法。该算法同时考虑了拟合模型系数矩阵误差与观测向量误差,并可在模型参量解算过程中,通过计算点与模型的相关关系,自适应地调整各点拟合权值,优化拟合权阵。模拟球面数据及实际扫描球面数据的拟合实例表明,该算法具备较好的可行性及优越性,利用该算法拟合得到的球心坐标可靠性更高。
(2) 基于IGGⅢ方案的加权总体最小二乘点云拟合算法较最小二乘法、总体最小二乘法更为稳健,但在解算过程中,当数据量过大时,由于权值的自适应修正过程较为复杂,迭代计算较为繁琐,解算所需时间较多,如何提高解算效率值得进一步深入研究。
基于IGGⅢ方案的加权总体最小二乘点云球面拟合
Fitting of sphere point clouds by weighted total least squares based on IGGⅢ scheme
-
摘要: 为了减少测量粗差对球标靶拟合精度的影响,在加权总体最小二乘法基础上,针对地面3维激光扫描球标靶数据特点,采用了权函数IGGⅢ方案,自适应地修正拟合权阵,构建了新的点云球面拟合方法。利用新方法分别拟合了模拟球面数据、实际扫描球面数据。结果表明,该方法在同时考虑拟合模型系数矩阵误差与观测向量误差基础上,通过合理定义及优化拟合权阵,获得了更为精确的球面参量。其拟合评价指标均优于常规方法。Abstract: In order to decrease the influence of observational gross error on the fitting precision of sphere target, aiming at data characteristics of sphere target by terrestrial 3-D laser scanning and based on weighted total least squares, weight function IGG Ⅲ scheme was adopted to adaptively modify the fitting weight matrix and a new fitting method of sphere point clouds was proposed. Simulated spherical datas and scanning spherical datas were fitted separately with the new method. The results show that, based on the consideration of both observation vector error and coefficient matrix error, more accurate sphere parameters are obtained by means of reasonable definition and optimization of fitting weight matrix. The fitting evaluation index of the new method is better than the conventional method's.
-
Table 1. Fitting precision without gross errors
methods Δ|a|/m Δ|b|/m Δ|c|/m Δ|r|/m $ {{\hat \sigma }_0}$ /m ${{\hat \sigma }_{\rm{s}}} $ /m LS method 0.0002 0 0.0016 0.0014 0.08004 0.00282 TLS method 0.0002 0 0.0015 0.0014 0.08004 0.00282 IGGⅢ-WTLS method 0.0005 0 0 0.0008 0.00112 0.00285 Table 2. Fitting precision with gross errors
methods Δ|a|/m Δ|b|/m Δ|c|/m Δ|r|/m $ {{\hat \sigma }_0}$ /m ${{\hat \sigma }_{\rm{s}}} $ /m LS method 0.0670 0.0285 0.1754 0.2409 5.21910 0.20223 TLS method 3.5674 0.9320 11.1511 7.7432 34.33430 2.39240 IGGⅢ-WTLS method 0.0026 0.0008 0.0035 0.0717 0.00530 0.20114 Table 3. Real spherical parameters and fitting precision
samples methods $ {\hat a}$ /m ${\hat b} $ /m $ {\hat c}$ /m $ {\hat r}$ /m Δ|r|/m $ {{\hat \sigma }_0}$ /m $ {{\hat \sigma }_{\rm{s}}}$ /m spherical Ⅰ LS method 0.0099 5.8443 -1.6388 0.0735 0.0010 7.7080×10-5 5.0800×10-3 TLS method 0.0099 5.8443 -1.6388 0.0735 0.0010 7.7080×10-5 5.0800×10-3 IGGⅢ-WTLS method 0.0083 5.8454 -1.6357 0.0724 0.0001 1.0440×10-6 9.4506×10-4 spherical Ⅱ LS method 1.3982 3.7690 -1.6291 0.0736 0.0011 8.2813×10-4 5.4274×10-3 TLS method 1.3982 3.7691 -1.6291 0.0736 0.0011 8.2813×10-4 5.4278×10-3 IGGⅢ-WTLS method 1.3963 3.7694 -1.6247 0.0717 0.0008 1.0084×10-5 7.0619×10-4 -
[1] LU T D, ZHOU Sh J. Sphere target fixing of point cloud data based on TLS[J]. Journal of Geodesy and Geodynamics, 2009, 29(4):102-105(in Chinese). [2] YUAN B, YUE D J, ZHAO Y Y. Spherical target positioning of terrestrial 3-D laser scanning based on robust weighted total least squares method[J]. Site Investigation Science and Technology, 2013(1):19-22(in Chinese). [3] LU T D, ZHOU Sh J. An iterative algorithm for total least squares estimation[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11):1351-1354(in Chinese). [4] OU J X, LI M F, WANG Y M. Plane fitting of point clouds based on robust weighted total least squares[J]. Journal of Geodesy and Geodynamics, 2014, 34(3):160-163(in Chinese). [5] LI M F, OU J X, TAN D. Study on fixed weight methods in plane fitting of point clouds based on weighted total least squares[J]. Journal of Geodesy and Geodynamics, 2015, 35(3):428-432(in Chinese). [6] CANG G H, YUE J P. Plane fitting of point clouds based on weighted total least squares adjustment[J]. Laser Technology, 2014, 38(3):307-310(in Chinese). [7] YUAN Q, LOU L Zh, CHEN W X. Applying weighted total least-squares to the plane point cloud fitting of terrestrial laser scanning[J]. Bulletion of Surveying & Maffing, 2011, 30(3):1-3(in Chinese). [8] SHEN Y Zh, LI B F, CHEN Y. An iterative solution of weighted total least-squares adjustment[J]. Journal of Geodesy, 2010, 85(4):229-238. [9] CHEN W X, CHEN Y, YUAN Q. Applycaion of weighted total least-squares to target fittiing of three-dimensional laser scanning[J]. Journal of Geodesy and Geodynamics, 2010, 30(5):90-96(in Chinese). [10] BURKHARD S, YARON A F. On the multivariate total least-squares approach to empirical coordinate transformations[J]. Journal of Geodesy, 2008, 82(6):373-383. doi: 10.1007/s00190-007-0186-5 [11] BURKHARD S, ANDREAS W. On weighted total least-square adjustment for linear regression[J]. Journal of Geodesy, 2008, 82(7):415-421. doi: 10.1007/s00190-007-0190-9 [12] GONG X Q, LI Zh L. A robust weighted total least squares method[J]. Acta Geodaetica Et Cartographica Sinica, 2014, 43(9):888-894(in Chinese). [13] WANG X Zh, TAO B Z, QIU W N. Advanced surveying adjustment[M]. Beijing:Survey and Mapping Press, 2006:73-89(in Chinese). [14] WANG H Y, ZHANG Y. Data processing of laser rangefinder based on robust estimation[J]. Journal of Atmospheric and Environmental Optics, 2007, 2(3):228-231(in Chinese). [15] WU J F, YANG Y X. Robust estimation for correlated GPS baseline vector network[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(3):247-251(in Chinese). [16] GONG X Q, LI Zh L. A roubust mixed LS-TLS based on IGGⅡ scheme[J]. Geomatics an Information Science of Wuhan University, 2014, 39(4):462-466(in Chinese). -


 网站地图
网站地图

 下载:
下载: