网站地图
-
近年来，直升机应用领域不断扩大。在中国抗战胜利70周年阅兵式上，20架直升机在空中排成了“70”的形状，是我国直升机编队飞行史上规模最大的一次。无线紫外光(ultraviolet, UV)通信是基于大气散射和吸收的无线光通信技术，“日盲”紫外光是指波长在200nm~280nm的紫外光，由于大气臭氧对太阳光的强烈吸收，使得该波段紫外光在近地表面具有全天候工作、背景噪声小、抗干扰能力强等优点[1]。无线mesh网络(wireless mesh network, WMN)具有自组织、多跳、高带宽等特性，有着较高的应用价值及前景[2-3]。mesh网络与紫外光通信具有各自的优势，将无线mesh网与紫外光通信相结合而组成的紫外光通信网络具有较好的性能[4]。编队飞行有助于取得空中优势，而将紫外光通信网络应用到编队飞行中，能够实现并保持机群在复杂环境下平稳飞行[5]。
KRISHNAMURTHY等人研究了非同构的6颗卫星可能出现的几种编队方式，并基于通信传感器拓扑结构的稳定性，研究了其稳定性对编队的影响[6]。海军工程大学的LIU等人将无线mesh网络应用于海战环境下的舰艇编队中，提高了海上通信网的保障能力，满足了海战保障体系高带宽和大容量的要求[7]。针对无人机编队内部以及编队与外部通信的需求，中国空间技术研究院西安分院的WU等人提出了一种无人机集群数据链组网的总体方案[8]。2015年，YANG等人通过考虑网络和节点特性，提出了日盲紫外光Ad hoc网络下一种稳定的路由协议[9]。
当任何一架飞机与机群失去联系时，会导致网络的拓扑结构发生改变，通信网络在链路断开后的通路恢复对整个通信网络连通性至关重要[10]，本文中主要研究在网络结构发生变化后如何快速恢复机群间通信路径，即当编队飞行通信网络中出现了链路中断和节点丢失情况，通过快速移动断开节点周围的节点来实现原最优路径的恢复。
-
将具有mesh网络特点的紫外光通信网络与直升机编队相结合，能够很好地满足直升机在复杂环境的下进行非直视、全天候的工作。分散结构[11]是指直升机编队中没有长机与僚机之分，各飞机在编队队形中地位平等。编队内部的节点通过多跳均可实现信息交换，相互配合完成任务[12]，如图 1所示。
Figure 1. Helicopters flying in formation
直升机编队网络拓扑图如图 2所示。图 2a中1~9分别表示9架直升机编号，图 2b中1~13表示13架直升机编号，其中每架直升机均使用多发多收的通信设备，直升机间保持此安全距离实现平稳飞行，飞机间的连线为通信链路，表示两个节点可直接通信，不直接相连的两个节点可通过多跳来实现通信，每架飞机至少有一条通路[13-14]。
Figure 2. Network topology of decentralized formation flight
-
紫外光通信衰减比较严重，随着通信距离的增加，路径损耗呈指数形式衰减，紫外光非视距(non-line-of-sight, NLOS)路径损耗L简化公式为[15]：
$ L = \xi {r^\alpha }{{\rm{e}}^{\beta r}} $
(1) 式中，r为通信距离; ξ为路径损耗因子; α为路径损耗指数; β为综合衰减因子，其与收发端几何角度有关。
在近距离通信中，综合衰减因子β所引起的衰减为(1~10)km-1，一般来说不考虑衰减因子β对路径损耗的影响，简化(1)式后可以得到近距离紫外光通信的路径损耗为[15]：
$ L = \xi {r^\alpha } $
(2) Dijkstra算法主要针对最优路径问题，作为经典的最优路径寻找方法而广泛应用于各种网络中，文中将路径损耗作为直升机编队飞行中的路径权值，其中路径权值是影响通信网络的连接质量和寻径效率的关键因素。由(2)式可得，收发端仰角及通信距离均直接影响着紫外光通信的路径损耗，具体表现为：增大通信距离的和收发仰角均会导致路径损耗增大；而增大接收视场角路径损耗则会减小[16]。
-
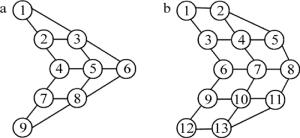
对于路径中的A→B→C形式，称A为B的上链路，C为B的下链路，以图 2a为例，若刚好某一条最优路径经过节点5，则其与邻节点断开情况与节点5的节点度有关，节点度为该节点与周围直接相连的节点数目。以节点5为例，与节点5相连的有4个节点，因此节点5的节点度d(k)=4，此时链路中断情况有3种，分别为：节点5与节点3断开；节点5同时与节点3和节点8断开；节点5同时与节点3、节点8和节点4断开。若当节点5周围4个节点全部断开时为节点中断情况。
-
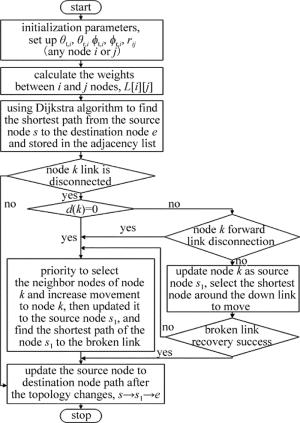
本文中提出的通路快速恢复算法(path fast recovery algorithm, PFRA)是指若最优路径中某条链路或某一节点完全断开时，原最优路径被分成了两部分，此时在断开的节点周围找到一个合适的节点，通过该节点的加速移动来实现原最优路径的恢复，图 3为本文中所涉及的通路快速恢复算法流程图。大体步骤可描述为：首先通过初始化产生一个满足条件的直升机编队飞行网络拓扑图；然后利用Dijkstra算法寻找整个网络中任意两点之间最优路径；断开某一节点的链路并判断链路断开情况；最后根据邻接表中存储的节点关系，选择断开节点周围最合适的节点向断开的链路快速移动来实现最优路径的恢复。
Figure 3. Flow chart of PFRA
(1) 初始化各个参量。直升机数目N，发射端仰角θt和发射角ϕt，接收端仰角θr和视场角ϕr，机群网络拓扑图为G，各节点的节点度为d(k)；(2)通过(2)式计算直接相连的两节点i和j之间路径损耗L[i][j], 并将该值作为节点间的路径权值。利用Dijkstra算法找出源节点s与目的节点e之间的最优路径并存储在邻接表中；(3)判断节点k周围链路是否断开。若中断，进行步骤(4)，否则跳到步骤(8)；(4)根据节点度判断链路断开状态。若d(k)=0，即节点k为丢失状态，进行步骤(5)，否则跳到步骤(6)；(5)在邻接表中选取节点k周围与上下链路直接或间接相连的节点向节点k加速移动，来实现原最优路径的恢复，并将该点更新为此时的源节点s1，然后进行步骤(7)；(6)判断断开链路是否为节点k的上链路，若是，执行步骤(5)，否则，更新节点k为此时源节点，在其下链路断开节点的周围选择能够与上链路直接或间接相连的节点快速移动，来实现原最优路径恢复，然后进行步骤(7)；(7)找到拓扑图改变后断开节点到目的节点的恢复路径，并更新邻接表；(8)算法结束。
-
对算法性能的评价，本文中主要用平均收敛时间来衡量。在衡量算法性能时，由于单次实验不能完全说明，因此本文中采用多次实验取平均值的方法。
平均收敛时间：反映算法的收敛速度，用$ {\bar T}$来表示，计算公式如下所示：
$ \bar T = \frac{1}{N}\sum\limits_{i = 1}^N {} {t_i} $
(3) 式中，N表示试验次数，ti表示第i次试验时算法的收敛时间。
-
算法的仿真是和路径恢复时间均是在MATLAB软件下进行的，先给定直升机数目(N=9个和N=13个)以及收发仰角和节点距离得到路径损耗，然后利用Dijkstra算法找出各节点之间的最优路径并存储在邻接表中。图 4中的PFRA表示上面提到的通路快速恢复算法，origin node代表从源节点重新寻找路径。
Figure 4. Simulation results of algorithm convergence time
图 4a和图 4b分别表示图 2a和图 2b断开节点在最优通信路径下的不同跳数对算法收敛时间的影响，其中横坐标为节点在最优路径中的跳数，纵坐标为收敛时间。从图 4a中可以看出，当断开的节点是最优路径中的第1跳时，采用本文中提出的PFRA算法和从源节点重新寻找路径的平均收敛时间几乎相同，这是因为当断开的节点是最优路径的第1跳时，均是从源节点开始恢复或重寻路径。另外，随着断开节点在最优路径中跳数的增大，从源节点重新寻找路径的收敛时间几乎不变，而采用本文中提出的PFRA算法，其收敛时间近似呈线性减小趋势；且断开节点越接近目的节点时，两种算法的收敛时间相差越大。从图 4b中同样可以看出，当从源节点到目的节点最优路径为4跳时，其曲线趋势与3跳节点相类似。即当断开的节点是最优路径中的第1跳时，采用本文中提出的PFRA算法和从源节点寻找最新路径的收敛时间也是几乎相同的，且跳数越大，收敛时间相差越大。
综上所述，当网络中某一节点断开时，本文中提出的PFRA算法比源节点重寻路径所用的收敛时间更小；且断开节点在最优路径中跳数越大，其收敛时间与从源节点重寻相差越大，因此本文中的PFRA算法的性能在很大程度上优于从源节点重寻方法。
-
图 2a的网络拓扑结构中，节点3、节点5、节点8的节点度均为4，对网络稳定性的影响相对较大，整个网络有A92=72条最优路径，节点数最多的最优路径1→3→5→8→9，除源节点和目的节点外节点跳数为3，接下来的分析将选择该路径来进行通信路径快速恢复研究。
当链路断开或节点中断时，假定直升机在空中的加速度为10m/s2，节点的移动原则为在最短的时间内，移动最少的节点来恢复原最优路径，且优先移动与断开链路的上下节点直接相连的节点，若满足条件的节点多于一个，则移动距离下链路短的节点。此时图 2a的路径恢复分析如表 1所示。
Table 1. Analysis of path recovery with three hop relay node
disconnected links node movement time/s path searching time/ms original optimal path restoration neighbor links of node 3 3-1 1.5 1.13 1→2→3→5→8→9 3-5 1.0 0.91 3→6→5→8→9 3-1, 3-5 0.7 1.08 1→2→4→5→8→9 3-1, 3-5, 3-2/6 0.7 1.06 1→2→4→5→8→9 neighbor links of node 5 5-3 1.0 0.93 3→6→5→8→9 5-8 0.6 0.81 5→6→8→9 5-3, 5-8 1.0 0.89 3→6→8→9 5-3, 5-8, 5-4/6 1.0 0.92 3→6→8→9 neighbor links of node 8 8-5 0.6 0.85 5→6→8→9 8-9 1.9 0.60 8→7→9 8-5, 8-9 1.9 0.81 5→4→7→9 8-5, 8-9, 8-7/6 1.9 0.79 5→4→7→9 由表 1可知，在第1跳节点链路断开时，当节点3的上链路断开时，即断开的链路为3-1时，此时到节点9的最优路径的寻找需要从节点1重新开始。而断开链路节点3在最优路径中的下链路，即断开的链路为3-5时，此时最优路径的寻找从节点3开始即可，相比较断开上链路，断开下链路时路径恢复时间有了明显的减小。
在第2跳节点链路断开时，若断开的是节点5的上链路，此时依然需要从节点3开始重新寻找到节点9的最优路径。而断开链路为节点5的下链路时，到节点9的最优路径的寻找只需要从节点5开始重即可，路径寻找时间同样短于从上链路重寻。
第3跳节点断开的情况与前两跳类似，断开下链路的路径恢复时延以及寻找时间与断开上链路相比均有明显改善，且节点8的下链路断开时，路径的恢复只需从节点8开始，此时的路径恢复时间是最优的，即此时的路径恢复是最容易的。
同理对图 2b，整个网络有A132=156条最优路径，此时节点1~13的最优路径为1→2→4→7→10→13，除去源节点与目的节点外，节点跳数为4，该最优路径下的通路恢复分析如表 2所示。
Table 2. Analysis of path recovery with four hop relay node
disconnected links node movement time/s path searching time/ms original optimal path restoration neighbor links of node 2 2-1 1.9 1.89 1→3→4→7→10→13 2-4 1.8 1.64 2→5→4→7→10→13 2-1, 2-4 1.9 1.86 1→3→4→7→10→13 2-1, 2-4, 2-5 1.9 1.88 1→3→4→7→10→13 neighbor links of node 4 4-2 1.8 1.85 2→5→4→7→10→13 4-7 2.5 1.51 4→3→6→7→10→13 4-2, 4-7 2.1 1.74 2→5→8→7→10→13 4-2, 4-7, 4-5/3 2.1 1.76 2→5→8→7→10→13 neighbor links of node 7 7-4 2.5 1.58 4→3→6→7→10→13 7-10 3.5 1.32 7→8→11→10→13 7-4, 7-10 3.0 1.47 4→3→6→9→10→13 7-4, 7-10, 7-6/8 3.0 1.43 4→3→6→9→10→13 neighbor links of node 10 10-7 3.5 1.35 7→8→11→10→13 10-13 1.2 1.05 10→11→13 10-7, 10-13 3.5 1.23 7→8→11→13 10-7, 10-13, 10-9/11 3.5 1.19 7→8→11→13 由表 2可得，4跳节点链路断开时的路径恢复情况与3跳节点相类似，与断开节点的上链路相比，断开下链路时的路径恢复时间较小，且越接近目的节点，其路径寻找时间越短。
当节点度d(k)=0时，即为节点断开情况。对图 2a中的拓扑结构节点断开时路径恢复分析如表 3所示。
Table 3. Analysis of path recovery with three hop node
failed node node movement time/s path searching time/ms node position path recovery section node 3 0.7 1.08 first hop 1→2→4→5→8→9 node 5 1.0 0.89 second hop 3→6→8→9 node 8 1.9 0.74 third hop 5→4→7→9 由表 3可知，当断开节点位于最优路径的第1跳时，其路径寻找时间是最长的，随着断开节点的位置越接近目的节点，其路径寻找时间越短。同理，对图 2b节点断开时的路径恢复如表 4所示。此时4跳节点的路径寻找时间变化趋势与3跳节点相类似，证明了该算法在很大程度上优于从源节点重寻方法。
Table 4. Analysis of path recovery with four hop node
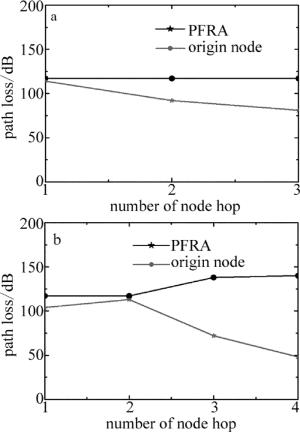
failed node node movement time/s path searching time/ms node position path recovery section node 2 1.9 2.15 first hop 1 →3→4→7→10→13 node 4 2.1 1.87 second hop 2→5→8→7→10→13 node 7 3.0 1.52 third hop 4→3→6→9→10→13 node 10 3.5 1.21 fourth hop 7→8→11→13 图 5a和图 5b为断开节点在最优路径不同跳数下，采用路径恢复算法与源节点重寻算法下的路径权值对比。可以看出，采用本文中提出的路径恢复算法所得到的新路径权值在开始时与从源节点重寻路径相比相差不大，随着节点在最优路径中跳数的增大，两种方法的路径权值相差越明显。这说明该算法虽然在节点移动方面需要花费时间，但是在收敛时间以及路径权值上有明显的减小，且越接近目的节点其优势越大。
Figure 5. Relationship between path loss and the number of node hop
综上所述，由于断开上链路时，路径的恢复需要从上邻节点开始，而断开下链路时，从该节点开始恢复即可，因此断开下链路时路径恢复时间更短；且随着断开的节点在最优路径中跳数的增大，路径寻找时间呈递减趋势。
-
本文中利用紫外光的路径损耗，并将路径损耗作为节点路径的权值，然后通过Dijkstra算法找到任意两点间的最优路径。在保证网络连通的前提下，提出了一种快速恢复链路断开或节点中断的算法。结果表明，断开同一节点的情况下，PFRA算法的平均收敛时间以及路径权值均小于从源节点重寻方法，且越接近目的节点，两种算法的收敛时间相差越大；当网络中某条链路断开或节点中断时，采用本文中提出的PFRA算法时，当断开的节点越接近目的节点时，其路径恢复时延越短，证明了该算法的优越性。
紫外光NLOS通信的机群间通路快速恢复算法
Path fast recovery algorithm of inter clusters for UV NLOS communication
-
摘要: 为了研究直升机编队飞行在链路中断或节点中断情况下的路径恢复，基于紫外光非直视通信的路径损耗，采用Dijkstra算法寻找网络连通性的前提下直升机编队飞行通信网络的最优路径，通过节点移动来实现链路中断或节点中断时的路径恢复。通过理论以及仿真分析，得到了最优路径在不同链路断开时的路径恢复情况。结果表明，采用所提出的算法虽然在节点移动时需要花费2s~3s的时间，但是与路径重寻方法相比，3跳和4跳节点的链路收敛时间能够有效减小0.2ms和0.4ms，路径权值同样能够减小20dB和45dB，因此该算法具有可行性。这一结果对机群间路径快速恢复的研究有一定的应用价值。Abstract: In order to study the path recovery of helicopter formation flying in the two cases of link expiration or node outage, based on the analysis of the path loss in ultraviolet (UV) non-line-of-sight (NLOS) communication. Dijkstra algorithm was adopted to find the optimal path of helicopters flying in formation communications network under network connectivity. Path recovery was achieved by node moving at link expiration or node outage. After theoretical simulation and analysis, the path recovery of the optimal path in different links expiration was obtained. The results show that although the algorithm spends 2s~3s time to move the nodes, compared with the paths re-search method, the convergence time of three-hop and four-hop node can effectively reduce 0.2ms and 0.4ms. The path weight also can reduce 20dB and 45dB. The algorithm is feasible and has applicable value for studying path fast recovery of inter clusters.
-
Key words:
- optical communication /
- ultraviolet /
- path recovery /
- formation flight /
- optimal path
-
Figure 2. Network topology of decentralized formation flight
a—nine node topology b—thirteen node topology
Figure 4. Simulation results of algorithm convergence time
a—three hop node b—four hop node
Figure 5. Relationship between path loss and the number of node hop
a—three hop node b—four hop node
Table 1. Analysis of path recovery with three hop relay node
disconnected links node movement time/s path searching time/ms original optimal path restoration neighbor links of node 3 3-1 1.5 1.13 1→2→3→5→8→9 3-5 1.0 0.91 3→6→5→8→9 3-1, 3-5 0.7 1.08 1→2→4→5→8→9 3-1, 3-5, 3-2/6 0.7 1.06 1→2→4→5→8→9 neighbor links of node 5 5-3 1.0 0.93 3→6→5→8→9 5-8 0.6 0.81 5→6→8→9 5-3, 5-8 1.0 0.89 3→6→8→9 5-3, 5-8, 5-4/6 1.0 0.92 3→6→8→9 neighbor links of node 8 8-5 0.6 0.85 5→6→8→9 8-9 1.9 0.60 8→7→9 8-5, 8-9 1.9 0.81 5→4→7→9 8-5, 8-9, 8-7/6 1.9 0.79 5→4→7→9 
下载: 导出CSV
Table 2. Analysis of path recovery with four hop relay node
disconnected links node movement time/s path searching time/ms original optimal path restoration neighbor links of node 2 2-1 1.9 1.89 1→3→4→7→10→13 2-4 1.8 1.64 2→5→4→7→10→13 2-1, 2-4 1.9 1.86 1→3→4→7→10→13 2-1, 2-4, 2-5 1.9 1.88 1→3→4→7→10→13 neighbor links of node 4 4-2 1.8 1.85 2→5→4→7→10→13 4-7 2.5 1.51 4→3→6→7→10→13 4-2, 4-7 2.1 1.74 2→5→8→7→10→13 4-2, 4-7, 4-5/3 2.1 1.76 2→5→8→7→10→13 neighbor links of node 7 7-4 2.5 1.58 4→3→6→7→10→13 7-10 3.5 1.32 7→8→11→10→13 7-4, 7-10 3.0 1.47 4→3→6→9→10→13 7-4, 7-10, 7-6/8 3.0 1.43 4→3→6→9→10→13 neighbor links of node 10 10-7 3.5 1.35 7→8→11→10→13 10-13 1.2 1.05 10→11→13 10-7, 10-13 3.5 1.23 7→8→11→13 10-7, 10-13, 10-9/11 3.5 1.19 7→8→11→13
下载: 导出CSV
Table 3. Analysis of path recovery with three hop node
failed node node movement time/s path searching time/ms node position path recovery section node 3 0.7 1.08 first hop 1→2→4→5→8→9 node 5 1.0 0.89 second hop 3→6→8→9 node 8 1.9 0.74 third hop 5→4→7→9
下载: 导出CSV
Table 4. Analysis of path recovery with four hop node
failed node node movement time/s path searching time/ms node position path recovery section node 2 1.9 2.15 first hop 1 →3→4→7→10→13 node 4 2.1 1.87 second hop 2→5→8→7→10→13 node 7 3.0 1.52 third hop 4→3→6→9→10→13 node 10 3.5 1.21 fourth hop 7→8→11→13
下载: 导出CSV
-
[1] ZHAO T F, KE X Zh. Research on technologies in solar blind ultraviolet Ad hoc network[J]. Application Research of Computers, 2010, 27(6):2204-2207(in Chinese). [2] FANG X M. Next generation wireless internet technology:wireless mesh networks[M]. Beijing:People's Posts and Telecommunications Press, 2006:5-27(in Chinese). [3] ZHAO T F, KE X Zh, HOU Zh M, et al. Link performance analysis of wireless ultraviolet network[J]. Laser Technology, 2011, 35(6):828-832(in Chinese). [4] ZHAO T F, KE X Zh, FENG Y L. Technology research in the solar blind ultraviolet wireless network[J]. Optical Communication Technology, 2007, 34(7):50-53(in Chinese). [5] SONG Y, ZHANG Ch, FANG Y G. Stochastic traffic engineering in multihop cognitive wireless mesh networks[J]. IEEE Transactions on Mobile Computing, 2010, 9(3):305-316. doi: 10.1109/TMC.2009.111 [6] KRISHNAMURTHY A, PREIS R. Satellite formation, a mobile sensor network in space[C]//Parallel and Distributed Processing Symposium, International.New York, USA: IEEE, 2005: 243a. [7] LIU X J, WU X Zh, HE R L. Research on application of warship fleet communication network based on wireless mesh networks[J]. Ship Electronic Engineering, 2012, 32(6):92-94(in Chinese). [8] WU P, TANG W Zh. The study of UAV flock network datalink[J]. Space Electronic Technology, 2012, 9(3):61-64(in Chinese). [9] YANG J, LUO J L, CHENG F, et al. A stability routing protocol for the solar blind ultraviolet Ad-hoc network[C]//2015 International Conference on Intelligent Systems Research and Mechatronics Engineering (ISRME 2015). Amsterdam, Netherlands: Atlantis Press, 2015: 926-930. [10] LI L, HALPERN J Y, BAHL P, et al. Analysis of a cone-based distributed topology control algorithm for wireless multi-hop networks[C]//Twentieth Association for Computing Machinery(ACM) Symposium on Principles of Distributed Computing. New York, USA: Association for Computing Machinery, 2001, 13(1): 147-159. [11] ZHANG L P, WEI R X, LIU Y. Decentralized optimal control for UAV formation forming[J]. Flight Dynamics, 2012, 30(1):25-28(in Chinese). [12] OU Ch J. UAVs formation flight control[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015: 1-69(in Chinese). [13] SONG Y, ZHANG Ch, FANG Y G. Stochastic traffic engineering in multihop cognitive wireless mesh networks[J]. IEEE Transactions on Mobile Computing, 2010, 9(3):305-316. doi: 10.1109/TMC.2009.111 [14] PURTA R, NAGRECHA S, MADEY G. Multi-hop communications in a swarm of UAVs[J]. Simulation Series, 2013, 45(1):32-39. [15] CHEN G, XU Zh Y, DING H P, et al. Path loss modeling and performance trade-off study for short-range non-line-of-sight ultraviolet communications[J]. Optics Express, 2009, 17(5):3929-3940. doi: 10.1364/OE.17.003929 [16] CHEN G, ABOUGALALA F, XU Zh Y, et al. Experimental evaluation of LED-based solar blind NLOS communication links[J]. Optics Express, 2008, 16(19):15029-15068. -
点击查看大图
图(5) / 表(4)
计量
- 文章访问数: 7738
- HTML全文浏览量: 5493
- PDF下载量: 184
- 被引次数: 0
