网站地图
下载:
-
1992年, ALLEN等人通过实验发现拉盖尔-高斯光束具有nh的轨道角动量[1](其中, n为拓扑荷数, 一般取整数，也可以为分数; h为普朗克常数)。由于n具有多取值性[2]和不同轨道角动量之间的正交性[2], 使得它成为一种新的被研究的自由度[3]。具有轨道角动量的涡旋光束相对于普通高斯光束的主要区别在于前者具有螺旋形的相位因子einθ，其中θ为相位角。涡旋光束在信息传输中具有保密性好、容量大、无频带限制、易于编解码等一系列优点，使得它广泛应用于光学操纵、生物医学、光镊技术、信息编码等方面[4]。涡旋光束在信息编码的应用方面已经进行了相当深入的研究并取得了一些新的进展[5]。正是这些成果使得基于涡旋光束的自由空间光通信系统受到了越来越多的重视。
大气湍流是影响自由空间光通信的一个关键因素[6]，同样的，大气湍流也是影响涡旋光束质量的重要因素。国内外早已开展了针对大气湍流的研究[7-10]，其中XING[7]等人研究了大气湍流对于激光通信系统的影响，在忽略其它噪声的影响下理论推导出了系统平均误比特率和大气湍流引起的光强起伏的关系。ZHU等人[8]研究贝塞尔-高斯涡旋光在湍流大气中的传播，提出涡旋光束可以由若干偏心高斯光束叠加而成，并理论推导了涡旋光束在传播过程中的平均光强表达式。MA等人[9]推导出了在斜程传输过程中通信系统误比特率和振幅起伏的关系。WANG等人[10]在ZHU的基础上讨论不同参量对贝塞尔-高斯涡旋光强的影响，并提出了桶中功率理论。YANG等人[11]研究了大气湍流对拉盖尔-高斯光束传播质量的影响。而参考文献[8]和参考文献[10]中主要介绍了不同湍流强度下贝塞尔-高斯涡旋光束在传播过程中光强分布和相位奇异性的理论分析，但并没有进行相关的数值仿真结果方面的验证，对在传播过程中可能影响光束质量的因素没有进行较为深入和全面的分析。作者在此基础上较为系统地分析了影响涡旋光束质量(主要是光强和相位)的主要因素，其中包括湍流强度、传输距离、激光波长、拓扑荷数等。为了验证结论的准确性，首先利用次谐波补偿法产生随机相位屏来模拟大气湍流，解决了传统随机相位屏模拟大气湍流过程中低频成分不足的问题。然后利用广义的惠更斯-菲涅耳原理理论推导出了贝塞尔-高斯涡旋光束在湍流大气传输中平均光强表达式。最后利用随机相位屏仿真了贝塞尔-高斯涡旋光束在大气湍流中的传输，采用控制变量法分析了可能影响光束质量的因素。理论分析和数值仿真结果吻合。相关的参考文献[11-12]也可以佐证部分结果的正确性。另外, 由于进行涡旋光束传播的实验需要性能较好的空间光调制器、较为适合的大气湍流模拟环境，长距离传输时较强抗干扰能力[13]等因素也导致实验部分的印证较为困难，目前国内外的相关研究[12-15]也以模拟仿真为主。
-
在自由空间光通信系统中影响通信质量的因素有很多，其中大气湍流[12-17]作为一种影响自由空间光通信传输系统的主要因素而受到人们越来越多的研究。一般来讲，大气湍流是在大气环境下随机分布的一种状态。而这种状态如果在光学领域里，它主要指的是由于诸如温度、压强等大气环境因素的随机变化而导致大气折射率出现随机性起伏的一种现象。大气折射率的随机变化被称为大气湍流，大气折射率起伏的强弱程度可用通过大气结构常数来表示。由于大气湍流所造成的光场随机分布状态在理论上进行推导是较为困难的，因此为了方便研究，大部分采用随机相位屏[18-21]干扰的方法对其进行相同效果的数值模拟，它是在Kolmogorov谱模型下利用快速傅里叶变换的功率谱反演法来产生的。作者数值模拟了涡旋光束在大气湍流传输过程中光强和相位分布的变化，其中采用了10层随机相位屏来进行叠加模拟，由于传统的均匀采样会造成随机相位屏大量低频信息泄露的问题，因此对相位屏进行了相应的低频补偿[21]。具体方法是：首先在快速傅里叶变换中需要对低频次谐波进行重采样, 然后再对利用功率谱反演变换得到的随机相位屏进行插值拟合, 这样产生随机相位屏的低频特性才得以补偿。
基于快速傅里叶变换的功率谱反演法[19-20]需要产生随机相位屏，首先生成一个频域内均值为0、方差为1的N×N维复随机数矩阵C(kx, ky), 其中大气折射变动频谱决定它的随机分布方差, 然后需要用符合大气湍流Kolmogorov谱的功率谱密度函数I0对复随机矩阵进行滤波, 再进行傅里叶逆变换得到随机相位屏ϕ(kx, ky)。
假定相位屏平面是x-y平面，光束在z方向上进行传输。现使用贝塞尔-高斯光束(Bessel-Gaussian beam, BGB)来模拟传输光束，光场用U表示，在z=0处，贝塞尔-高斯涡旋光束光场表达式为:
$ \begin{array}{*{20}{c}} {{U_0}\left( {x,y} \right) = {{\rm{J}}_n}\left( {\beta \sqrt {{x^2} + {y^2}} } \right) \times }\\ {\exp \left[ { - \frac{{{x^2} + {y^2}}}{{{w^2}\left( z \right)}}} \right]\exp \left( {{\rm{i}}n\theta } \right)} \end{array} $
(1) 式中, β为波矢横向的分量，Jn为n阶的贝塞尔函数，n为阶数，同时也是贝塞尔-高斯光束的拓扑荷数，θ为相位角，w(z)为z处的束腰半径。
当贝塞尔-高斯光束在自由空间传输时，其传输函数可表示为:
$ {U_{{\rm{prop}}}}\left( {{k_x},{k_y}} \right) = \exp \left[ {{\rm{i}}\Delta z\left( {k_0^2 - k_x^2 - k_y^2} \right)} \right] $
(2) 式中，kx和ky依次表示x轴和y轴方向上的频率波数谱，k0=2π/λ为光束的波数, λ为波长，Δz表示光束传输距离。当光束到达第1个相位屏时, 其光场可表示为:
$ {U_{1 - }}\left( {x,y} \right) = {{\mathscr{F}}^{ - 1}}\left\{ {{\mathscr{F}}\left[ {{U_0}\left( {x,y} \right)} \right]{U_{{\rm{prop}}}}\left( {{k_x},{k_y}} \right)} \right\} $
(3) 涡旋光束经过相位屏影响再穿过它后其光场变成:
$ {U_{1 + }}\left( {x,y} \right) = {U_{1 - }}\left( {x,y} \right)\exp \left[ {{\rm{i}}{\mathit{\boldsymbol{\phi}}} \left( {x,y} \right)} \right] $
(4) 式中，U1+(x, y)表示相位屏的随机分布, ϕ(x, y)为x域中的相位屏。当到下一个相位屏时，这个过程将被依次重复迭代，一直到达最后一个相位屏。由于随机分布相位屏反映的是大气折射率变动下的随机复域值，在数值仿真模拟时可采用N×N复数组来表示，其中该数组的随机分布方差主要取决于大气折射变动频谱的变化。一般常见的频谱是基于Kolmogorov的大气折射率变动频谱：
$ {\mathit{\Phi }_n}\left( {{k_x},{k_y}} \right) = 0.033C_n^2{\left( {k_x^2 + k_y^2} \right)^{ - 11/6}} $
(5) 修正后的频谱能更加准确地描述大气湍流的变化。
$ \begin{array}{*{20}{c}} {{\mathit{\Phi }_n}\left( {{k_x},{k_y}} \right) = 0.033C_n^2 \times }\\ {\left[ {1 + 1.802\sqrt {\frac{{k_x^2 + k_y^2}}{{{k^2}}}} - 0.254{{\left( {\frac{{k_x^2 + k_y^2}}{{{k^2}}}} \right)}^{ - 7/12}}} \right] \cdot }\\ {\exp \left( {\frac{{k_x^2 + k_y^2}}{{{k^2}}}} \right){{\left( {k_x^2 + k_y^2 + \frac{1}{{L_0^2}}} \right)}^{ - 11/6}}} \end{array} $
(6) 式中, Cn2是折射率结构常数，L0是湍流的外尺度，l0表示湍流的内尺度。定义k=3.3/l0，又因为相位频谱和折射率频谱存在如下关系：
$ \mathit{\Phi }\left( {{k_x},{k_y}} \right) = 2{\rm{ \mathsf{ π} }}k_0^2\Delta z{\mathit{\Phi }_n}\left( {{k_x},{k_y}} \right) $
(7) 可以得到随机相位屏频谱的方差：
$ {\sigma ^2}\left( {{k_x},{k_y}} \right) = {\left( {\frac{{2{\rm{ \mathsf{ π} }}}}{{N\Delta x}}} \right)^2}\mathit{\Phi }\left( {{k_x},{k_y}} \right) $
(8) 式中，Δx是每个栅格之间的距离，N是栅格的数目(即复矩阵维数)。通过快速傅里叶变换，可以得到x域中的相位屏为:
$ {\mathit{\boldsymbol{\phi}}} \left( {x,y} \right) = {\mathscr{F}}\left[ {\mathit{\boldsymbol{C}}\left( {{k_x},{k_y}} \right)\sigma \left( {{k_x},{k_y}} \right)} \right] $
(9) 式中，C是一个N×N维复随机数矩阵，它的均值为0，方差为1。
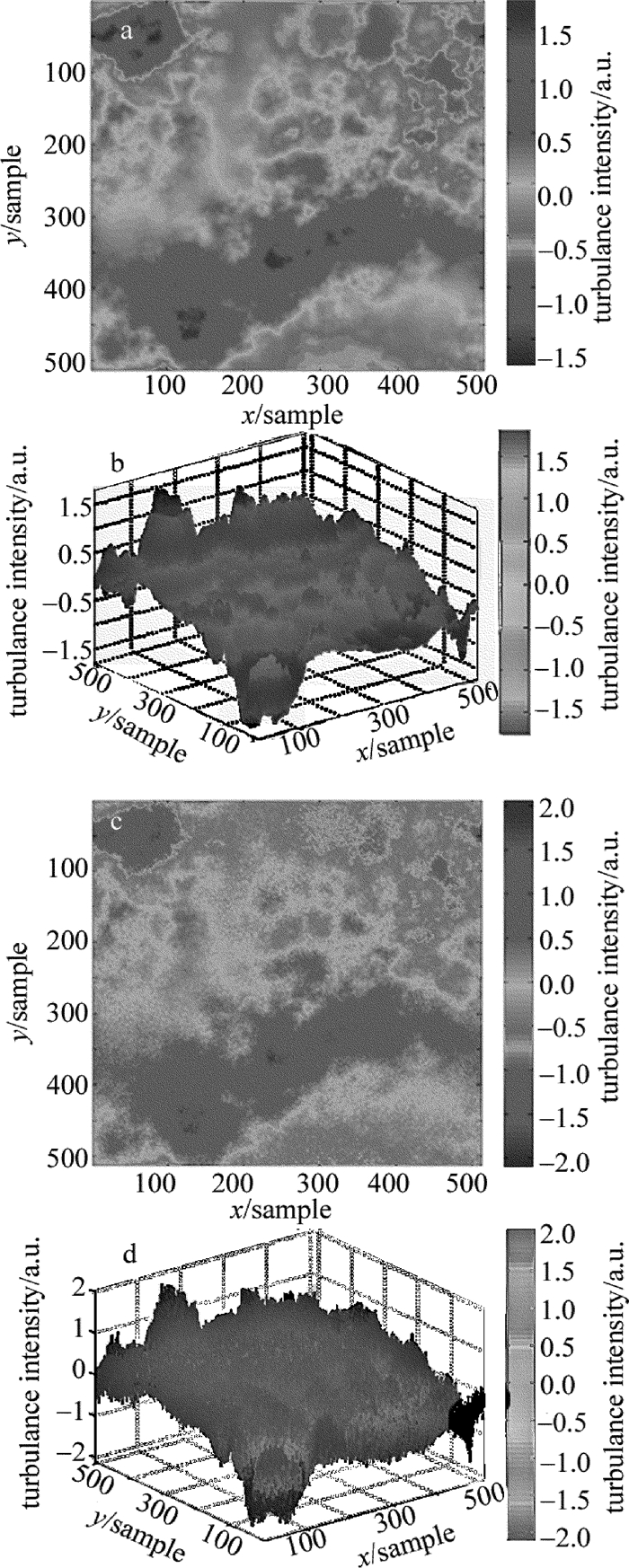
采用MATLAB实现随机相位屏仿真，其中以快速傅里叶变换为基础，增加了低频次谐波补偿。图 1a和图 1b表示均匀采样后随机相位屏的2-D和3-D光强分布图; 图 1c和图 1d表示增加了次频谐波补偿后的2-D和3-D随机相位屏。通过比较发现, 图 1c和图 1d比图 1a和图 1b更倾斜、模糊，低频成分明显。通过MATLAB仿真表明：利用次谐波补偿方法使得随机相位屏低频分量的得到了明显改善，通过增加了次谐波的采样，使得相位屏的仿真也变得更加准确。
Figure 1. 2-D and 3-D map of random phase screen
-
为了分析涡旋光束在大气湍流传输的特性，从理论上推导了系统平均光强[8]的表达式。由参考文献[8]和参考文献[10]可知，一个贝塞尔-高斯光束可以近似表达为若干个(一般取12)偏心高斯光束的叠加，该方法的准确性已在参考文献中得到分析论证。在光源z＝0空域中BGB涡旋光束的场强为:
$ E\left( {x,y,0} \right) = \sum\limits_{m = 1}^{M - 1} {{E_m}\left( {x,y,0} \right)} $
(10) 基于广义的惠更斯-菲涅耳原理，湍流大气下贝塞尔-高斯涡旋光束在传输到z时, 其输出端横截面内的平均光强可表示为[10]:
$ \begin{array}{*{20}{c}} {\left\langle {I\left( {x,y,z} \right)} \right\rangle = \frac{{N_w^2}}{{{M^2}\mathit{\Omega }}} \times }\\ {\exp \left\{ { - \frac{{{R^2}\left( {1 + w_0^2/\rho _0^2} \right)}}{{2\mathit{\Omega }w_0^2}} - \frac{{2N_w^2{x^2} + {y^2}}}{{w_0^2}}} \right\} \cdot }\\ {\sum\limits_{m,l}^{M - 1} {\exp \left[ {{\rm{i}}\left( {{\varphi _m} - {\varphi _l}} \right) + \frac{{{R^2}\cos \left( {{\theta _m} - {\theta _l}} \right)}}{{2\mathit{\Omega }\rho _0^2}}} \right]} \cdot }\\ {\exp \left[ {\frac{{{N_w}\left( {1 + {\rm{i}}{N_w}} \right)R}}{{\mathit{\Omega }w_0^2}}\left( {x\cos {\theta _m} + y\sin {\theta _m}} \right) + } \right.}\\ {\left. {\frac{{{N_w}\left( {1 - {\rm{i}}{N_w}} \right)R}}{{\mathit{\Omega }w_0^2}}\left( {x\cos {\theta _l} + y\sin {\theta _l}} \right)} \right]} \end{array} $
(11) 式中，λ=632.8nm，复合个数M=12，Cn2=10－14m－2/3，定义R=2w0, 相位常量φm=nmα0，定义α0=2π/M，相位角θl=lα0, θm=mα0，束腰宽度w0=0.03m，拓扑荷数n=2, 传输距离z=1000m，Ω=1+Nw2+2w02/ρ02, ρ0=(0.545Cn2k02z)3/5, Nw为菲涅耳数。
图 2反映的是涡旋光束在大气湍流中系统归一化的平均光强分布，图 3表示涡旋光束在传播过程中强度和相位的数值仿真。其中图 2a表示在湍流强度分别为10-13m－2/3，10-14m－2/3，10-15m－2/3时系统归一化的平均光强分布，图 3a是其在相同湍流条件下通过随机相位屏模拟产生的涡旋光2-D光强、3-D光强和相位的数值仿真结果。由图可知，在湍流不断增强的过程中，涡旋光束会逐步退化为普通高斯光束，实际数值仿真过程中可以发现, 光强起伏会逐渐变大，强度逐步减弱，相位畸变也越来越严重，光束暗中空半径逐渐变小并逐步向高斯光束退化。图 2b表示在传输距离为1000m，3000m，5000m时系统归一化的平均光强分布，图 3b为相同传输距离下涡旋光束的相位和光强的数值仿真。由结果可以看出, 随着传输距离的增加, 涡旋光会逐渐退化为高斯光束，光强强度减弱，且光束会出现展宽效应但相位改变不太明显。图 2c反映了取拓扑荷数分别为n=1, n=4, n=7时系统归一化的平均光强分布，图 3c为取相同拓扑荷数下对应光强和相位的数值仿真。结果表明：涡旋光束的暗中空半径随着拓扑荷数的增大而增大，拓扑荷数越小的涡旋光束抗退化为普通高斯光束的能力越弱，但其相位畸变程度逐步变弱。图 2d是取激光波长分别为0.632μm，1.06μm，1.55μm时系统归一化的平均光强，图 3d为对应的数值仿真。通过结果可以发现, 随着波长的不断增加, 光束的抗退化为普通高斯光束的能力越强，数值仿真发现环形光强度不断增强，且相位畸变现象越微弱。所以选取波长较长的光束有较强的湍流抑制能力，能较好地在自由空间光通信系统传播。
Figure 2. Average intensity distribution of the system in atmospheric turbulence
Figure 3. Numerical simulation of intensity and phase of vortex beam in the process of propagation
-
首先采用次谐波低频补偿法解决了采样产生低频成分不足的问题，理论分析并数值仿真了贝塞尔-高斯涡旋光束在大气湍流中的传输特性。研究表明：湍流越强，贝塞尔-高斯涡旋光束的环形光强越弱，相位畸变也越严重，光强起伏越明显，且会逐渐退化为普通高斯光束；随着传输距离的增加，涡旋光束的光强起伏和衰减越严重，且有逐步向普通高斯光束退化的趋势；拓扑荷数越小的涡旋光束抗退化为普通能力差，但其相位畸变程度变小；波长较长的涡旋光束在传输过程中具有较强的抑制湍流能力。综上所述，涡旋光束在自由空间光通信系统中的传输质量和自身因素包括拓扑荷数、激光波长以及外部因素包括湍流强度、传输距离等密切相关。
大气湍流中贝塞尔-高斯涡旋光束传播性能分析
Performance analysis of Bessel-Gaussian vortex beam's propagation in atmospheric turbulence
-
摘要: 为了研究涡旋光束在湍流大气中的传输特性，根据广义的惠更斯-菲涅耳原理，采用基于快速傅里叶变换的功率谱反演法，对贝塞尔-高斯光束在大气湍流中的传输过程进行了理论分析和数值仿真; 采用次谐波补偿法产生随机相位屏来模拟大气湍流，解决了大气湍流模拟时存在低频成分不足的问题。结果表明，除了湍流强度外，传输距离、拓扑荷数、激光波长等也成为影响贝塞尔-高斯涡旋光束质量的主要因素; 湍流越强，光束的环形光强越弱，相位畸变越严重，光强起伏越明显，且逐渐退化为普通高斯光束; 随着传输距离的增加，涡旋光束扩散现象明显，最终退化为普通高斯光束; 波长越长，则涡旋光束抑制湍流能力越强，环形光强越强，相位畸变程度会得到逐步改善; 拓扑荷数越小，涡旋光束会最先退化为普通高斯光束，相位畸变程度越弱。该结果对于研究涡旋光束在自由空间光通信中的传输是有帮助的。
-
关键词:
- 光通信 /
- 自由空间 /
- 大气湍流 /
- 随机相位屏 /
- 贝塞尔-高斯涡旋光束
Abstract: In order to study the transmission characteristics of vortex beams in atmospheric turbulence, based on the generalized Huygens-Fresnel principle, the transmission process of Bessel-Gaussian beams (BGB) in atmospheric turbulence was analyzed theoretically and simulated numerically by using power spectrum inversion method based on fast Fourier transform. Harmonic compensation method was used to generate random phase screen to simulate atmospheric turbulence, which solved the problem that low frequency components were not enough. The results show that, besides turbulence strength, transmission distance, topological charge number and laser wavelength also become the main factors that could affect the vortex beam's communication quality. With the increasing of turbulence strength, the annular intensity decreases, phase distortion becomes more serious, intensity fluctuation is more obvious and beam will gradually degenerate into ordinary Gaussian beam. With the increase of transmission distance, vortex beam has the significant broadening and finally degrades into ordinary Gaussian beam. The longer the laser wavelength is, the stronger the ability which vortex beams restrain turbulence, the stronger annular light intensity is. In the meanwhile, the degree of phase distortion becomes weaker. The smaller topological charge number is, the weaker phase distortion is, and vortex beam would degenerate into ordinary Gaussian beams more easily. The results are helpful for the study of the propagation of vortex beams in free space optical communication. -
Figure 2. Average intensity distribution of the system in atmospheric turbulence
a—λ=632.8nm, w0=0.03m, n=2, z=1000m b—λ=632.8nm, w0=0.03m, n=2, Cn2=10-14m-2/3 c—λ=632.8nm, w0=0.03m, z=1000m, Cn2=10-14m-2/3 d—w0=0.03m, n=2, z=1000m, Cn2=10-14m-2/3
-
[1] ALLEN L, BEIJERSBERGEN M W, SPREEUW R J, et al. Orbital angular momentum of light and the transformation of Laguerre-Ganssian laser modes[J]. Physical Review, 1992, A45(3): 8185-8189. [2] ZHAO Sh M, JIANG X Ch, GONG L Y, et al. Communications using orbital angular momentum multiplexing[J]. Journalof Nanjing University of Posts and Telecommunications (Science Edition), 2015, 35(6): 1-12(in Chinese). [3] YUANX C, JIA P, LEI T, et al. Optical vortiees and optical communicationwith orbital angular momentum[J]. Journal of Shenzhen University (Science and Engineering Edition), 2014, 31(4): 331-346(in Chinese). doi: 10.3724/SP.J.1249.2014.04331 [4] DU J, WANG J. High-dimensional structured light coding/decodingfor free-space optical communicationsfree of obstructions[J]. Optics Letters, 2015, 12(9):4827-4830. [5] WANG J, HUANG H, YAN Y, et al. Terabit free-space data transmission employing orbital angular momentummultiplexing[J]. Nature Photonics, 2012, 6(7):488-496. doi: 10.1038/nphoton.2012.138 [6] WANG B. Study on the turbulence mitigation scheme in free-space optical communications using orbital angular momentum multiplexing[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2014: 1-73 (in Chinese). [7] XING J B, XU G L. Effect of the at mospheric turbulence on laser communication system[J].Acta Photonica Sinica, 2005, 34(12):1850-1852 (in Chinese). [8] ZHU K Ch, ZHOU G Q.Propagation of Bessel-Gaussian beams with optical vortices in turbulent atmosphere[J]. Optics Express, 2008, 16(26): 21315-21320. doi: 10.1364/OE.16.021315 [9] MA Ch L, CUI Y Sh.Analysis of effect of atmospheric turbulenceon laser communication system[J]. Infrared, 2010, 31(8):24-27 (in Chinese). [10] WANG H Y. CHEN Ch L.Propagation of Bessel-Gaussian beams with optical vortices in turbulent atmosphere[J]. Acta Photonica Sinica, 2013, 42(5): 506-510(in Chinese). [11] YONG Ch Y, ZHANG W. Effects of atmospheric turbulence on the Laguerre-Gaussian beams propagation[J]. Journal of Optoelectronics·Laser, 2014, 25(11): 2245-2251 (in Chinese). [12] ZOU L, ZHAO Sh M.The effects of atmospheric turbulence on the orbital angular momentum-multiplexed system[J].Acta Optica Sinica, 2014, 43(9): 0901001(in Chinese). [13] WANG G L. Crosstalk and suppression method research of OAM-multiplexed communication system in the model of atmospheric turbulence[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2015: 1-93(in Chinese). [14] YANG J, WANG H, ZHANG X. Influence of atmospheric turbulence on Rayleigh range of partially coherent laser[J]. Laser Technology, 2016, 40(3): 456-460 (in Chinese). [15] JING M, LI K N, TAN L Y. Exact error rate analysis of free-space optical communications with spatial diversity over Gamma-Gamma atmospheric turbulence[J]. Journal of Modern Optics, 2015, 63(3): 252-260. [16] SHIRAI T, DOGARIU A, WOLF E. Mode analysis of spreading of partially coherent beams propagating through atmospheric turbulence[J].Journal of Modern Optics, 2013, 20(6): 1094-1102. [17] WANG K M, LIU B, ZHANG L J, et al. Review of coded modulation free space optical communication system[J]. China Communications, 2015, 12(11): 1-17. [18] WANG L J, LI Q. Numerical simulation and validation of phase screen distorted by atmospheric turbulence[J]. Opto-electronic Engineering, 2007, 34(3): 1-4(in Chinese). [19] CAI D M, WANG K. Sampling methods of power spectral density method simulating atmospheric turbulence phase screen[J]. Acta Physica Sinica, 2014, 63(10): 104217(in Chinese). [20] CAI D M, TI P P.Fast simulation of atmospheric turbulence phase screenbased on non-uniform sampling[J]. Acta Physica Sinica, 2015, 67(22):224217(in Chinese). [21] ZHANG J Zh, ZHANG F Zh, WU Y.Methods for simulating turbulentphasescreen[J].High Power Laser and Particle Beams, 2012, 24(10): 2318-2324(in Chinese). doi: 10.3788/HPLPB -
点击查看大图
图(3)
计量
- 文章访问数: 7557
- HTML全文浏览量: 5564
- PDF下载量: 26
- 被引次数: 0
