网站地图
-
随着用户对遥感仪器需求的提高，能够适应恶劣空间温度环境的反射镜支撑技术越来越成为关注的重点。以地球同步轨道三轴稳定卫星平台上的光学有效载荷为例，载荷外热流昼夜变化大，空间反射镜工作力学环境复杂，光学系统在轨温度变化范围取决于载荷所采用的整体热控水平，提高光学系统的温度适应能力将有效减轻热控设计的压力，同时减轻热控重量。双脚架(bipod)柔性支撑技术能够较好地卸载温度变化带来的应力[1]，是未来大口径和恶劣空间温度环境反射镜支撑技术的主流方向。
反射镜支撑的主要目的是在有效地进行定位的同时，隔离机械附加载荷，尤其是温度变化产生的附加载荷，减小反射镜面形变形，以保持仪器成像质量。产生机械附加载荷的原因还有：力矢量变化、振动、加工装配误差、加工残余应力等等[2]。静定支撑对机构的约束数量等于机构的自由度数量。当加工误差、装配误差、温度变化引入形变的时候，静定支撑结构能够有效卸载，对反射镜不产生附加应力。静定支撑通常要求理想的铰链约束，但在现实中由于加工误差、摩擦、装配等原因理想铰链难以实现。超静定支撑存在过约束，支撑会产生附加应力，影响镜面面形。多点支撑通常是超静定支撑。准静定支撑可以有效隔离外部因素对反射镜的影响，实际设计可实现，有广泛的应用。欧洲空间局下一代对地观测卫星(第3代气象卫星)搭载的柔性组合成像仪上即采用了周边双脚架支撑结构[3]。美国的詹姆斯·韦伯天文望远镜中大量应用了双脚架支撑结构，包括反射镜支撑以及各个设备模块间的连接[4]。中国科学院长春光学精密机械与物理研究所对小型反射镜周边双脚架支撑结构的应用也进行了研究[5]。
本文中论述了一种空间反射镜背部双脚架支撑结构设计方法，支撑对象为直径335mm的圆形反射镜，设计要求在1g重力垂直光轴的工况下，反射镜面形精度均方根值(root mean square, RMS)小于12.7nm(λ/50, λ=632.8nm)，组件1阶频率高于100Hz。首先研究了双脚架支撑原理，针对双脚架结构参量、柔性铰链结构参量等方面进行了优化设计，并利用有限元方法对反射镜组件进行了力学、模态、热力学仿真分析，设计得到了一种背部双脚架柔性支撑结构，提出了背部双脚架支撑重点设计参量，在满足光学设计指标要求的同时具有足够的强度和刚度。设计过程中引入参量化建模仿真方法，有效提高了设计效率。
-
从支撑位置上分析反射镜的支撑方式主要有中心支撑、周边支撑、侧面支撑、背部支撑等几个类型[6]：中心支撑是以光学反射镜的中心孔为定位基准，主反射镜在空间微重力的作用下边缘变形较明显，适用于质量主要集中在中心部位的主反射镜；周边支撑以光学反射镜的底面及某一个长边的侧面为定位基准面，支撑结构简单、镜座外形尺寸大、质量大、无装配应力；侧面支撑通常用于长条形反射镜，以光学反射镜的两个侧面为定位基准；背部支撑以光学反射镜的背部为定位基准，是大口径反射镜使用最多的结构型式，在3点背部支撑的基础上发展了若干形式。
本文中主要考虑反射镜口径和空间尺寸限制来确定方案。一方面反射镜属于圆形中大型口径，质量分布相对均匀，不适合中心支撑和侧面支撑；周边支撑需要设计尺寸大、质量大的框架结构，相比之下背部支撑方式能够有效减轻支撑结构重量。另一方面，对于离轴三反光学系统，反射镜径向的空间相对拮据，轴向的空间相对宽裕，相比需要增加径向尺寸的周边支撑，背部支撑的双脚架支撑结构能有效节约径向空间，对离轴三反式光学系统有一定的实践意义。综上所述，方案采用背部支撑。同时为了有效卸载附加应力，方案采用双脚架准静定结构。
-
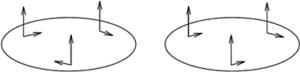
双脚架支撑系统由3个双脚架元件组成, 如图 1所示。理想的双脚架元件由两个杆件及4个球铰链转动副组成。根据修正的Kutzbach-Gruebler公式计算支撑系统的空间机构自由度[7]:
$ M = d\left( {n - m - 1} \right) + \sum\limits_{i = 1}^m {} {f_i} + v - \zeta $
(1) 
Figure 1. Theoretical models of two types of mount
式中, M为空间机构自由度; d为机构阶数，对于一般空间机构, d=6;n为构件数量; m为运动副数量; fi为第i个运动副的自由度; v为冗余自由度; ζ为局部自由度。双脚架支撑系统的自由度为：
$ {M_{\rm{b}}} = 6 \times \left( {8 - 12 - 1} \right) + 12 \times 3 - 6 = 0 $
(2) 实现了静定约束。相比较而言，改进型的背部3点支撑通常会在支撑与反射镜的连接处引入一个柔性铰链来实现球铰链转动副的功能，其自由度为:
$ {M_{{\rm{tri}}}} = 6 \times \left( {2 - 3 - 1} \right) + 3 \times 3 = - 3 $
(3) 仍然存在过约束，外部施加的机械附加载荷会传递到反射镜上，影响镜面面形。因此双脚架结构在理论上有较好的支撑效果。
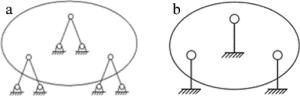
双脚架的排列方向要求线性无关，通常有图 2所示的两种方式，前者排列呈中心对称，适合圆形反射镜，后者适合其它形状的反射镜，如矩形反射镜[8]。
Figure 2. Arrangement manner of bipod
-
具有较强温度适应能力的光学系统，对结构材料的选择主要考虑两个方面：(1)要求有良好的强度及刚度，保证结构在发射、运行过程中不发生强度破坏和刚度失稳；(2)要求有合适的线膨胀系数，减少材料热变形系数不匹配带来的附加热应力。本文中结构设计采用的材料特性如表 1所示。其中反射镜采用的超低热膨胀系数(ultra-low expansion, ULE)是一种二氧化钛-硅酸盐玻璃，其绝对热膨胀系数(coefficient of thermal expansion, CTE)在5℃~35℃内极低，因此热稳定性极好。同时ULE密度小，冷热加工性能良好，材料制备、光学加工和工程应用也较成熟[9]。为了与其匹配选择系数较为接近的铁镍合金4J32作为支撑接头的材料。弹性元件则采用TC4钛合金，钛合金具有高强度、低密度的特点，常作为弹性元件的材料，保证结构在有较好形变能力的同时不发生强度破坏。
Table 1. Material properties of primary mirror components
materials density ρ/(103kg·m-3) Young’s modulus E/GPa yield strength σs/MPa Poisson’s ratio μ CTE α/10-6K-1 TC4 4.43 109 860 0.31 8.8 4J32 8.13 148 276 0.29 0.31 ULE 2.210 67 — 0.17 0.015 -
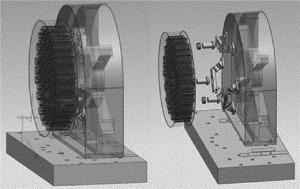
设计的反射镜支撑结构如图 3所示，采用反射镜、支撑接头、双脚架柔性元件、背板、振动板依次连接的方案。支撑接头通过胶粘接在反射镜背孔内，通过螺钉与双脚架柔性元件连接；3个柔性元件连接到背板上，背板与振动板相连。利用双轴柔性铰链实现双脚架柔性元件结构。双轴柔性铰链是由两个单轴柔性铰链正交放置组成，近似实现万向铰链的功能。1个双脚架柔性元件包含4个球铰链转动副，需要4个双轴柔性铰链实现。由于反射镜为圆形反射镜，3个双脚架元件呈中心对称放置。
Figure 3. Sketch of support structure of reflector
-
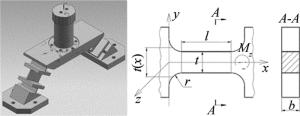
反射镜支撑系统的设计原则之一是减少摩擦带来的不确定性。在双脚架的理论模型中存在12个球铰链约束，传统由球铰链来实现，这种实现方式装配结构复杂，存在摩擦，需要润滑，在真空环境中容易引入污染源污染光学元件。本设计中采用柔性万向铰链结构实现球铰链约束。柔性铰链的优点有：可以整体化设计和加工、简化了结构、减小了体积和质量、不需要装配；没有摩擦和间隙，可实现高精度运动；没有磨损，提高组件寿命；不需要润滑，避免污染光学元件[10]。但是柔性铰链会减小组件刚度，需要根据实际刚度要求设计尺寸参量。柔性铰链主要分为开口式和叶片式两种[11]，实际分析时发现，双脚架结构需要柔性铰链具有较大的柔性，考虑采用柔性较好的叶片式结构。柔性铰链结构见图 4。由图 4理论推导计算得到单个柔节的弯矩和转角的关系。柔节厚度可表示为:
$ t\left( x \right) = \left\{ \begin{array}{l} t + 2\left[ {r - \sqrt {x\left( {2r - x} \right)} } \right], \left( {x \in \left[ {0, r} \right]} \right)\\ t, \left( {x \in \left[ {r, l - r} \right]} \right)\\ t + 2\left\{ {r - \sqrt {\left( {l - x} \right)\left[ {2r - \left( {l - x} \right)} \right]} } \right\}, \\ (x \in \left[ {l - r, l} \right]) \end{array} \right. $
(4) 
Figure 4. Structure of flexure hinge and its theoretical model
则绕z轴转动的柔性系数C计算为:
$ \begin{array}{l} C = \int_0^l {} \frac{1}{{EI(x)}}{\rm{d}}x = \frac{{12}}{{Eb}}\int_0^l {} \frac{1}{{{t^3}(x)}}{\rm{d}}x = \frac{{12}}{{Eb}}\left[ {\frac{{l - 2r}}{{}}{t^3}} \right. + \\ \frac{{2r\left( {6{r^2} + 4rt + {r^2}} \right)}}{{{t^2}\left( {2r + t} \right){{\left( {4r + t} \right)}^2}}} + \\ \frac{{12{r^2}\left( {2r + t} \right)}}{{\sqrt {{t^5}{{\left( {4r + t} \right)}^5}} }}{\rm{tan}}{{\rm{h}}^{ - 1}}\sqrt {1 + \frac{{4r}}{t}} ] \end{array} $
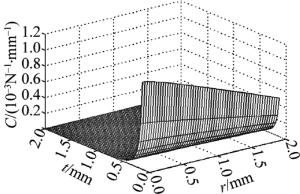
(5) 式中, I代表强度, E代表弹性模量，b代表截面宽度，l代表柔节长度，t代表柔节厚度，r代表圆角半径。材料一定时，柔度和截面宽度b成反比，和柔节长度l成正比，利用MATLAB分析t和r对柔性的影响结果, 如图 5所示。可以直观地看出厚度t对柔性的影响较大，厚度t越小，柔性越大，且呈非线性关系; 圆角半径r对柔性的影响较小，设计时优先选择合适的t值。
Figure 5. Influence of blade thickness and radius of fillet on flexibility
-
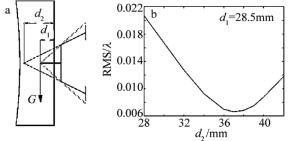
一般设计双脚架结构常采用周边粘接的形式，支撑脚延长线交点位置d2和粘接点位置d1重合(d1=d2)，设计时不分开考虑。由于背部支撑存在悬臂梁结构，当反射镜光轴垂直重力方向放置时，悬臂梁引入的柔性降低了双脚架结构对变形的吸收效果，适当设计支撑脚延长线交点位置可以有效补偿悬臂梁的变形，提高面形精度，对背部双脚架支撑结构设计有借鉴意义。
本文中结构将延长线交点位置d2与粘接位置d1分别设计，有效地提高了面形精度。如图 6所示，粘接位置d1=28.5mm时，延长线交点位置从d2=28.5mm改为d2=37mm，面形精度RMS从0.0193λ提高到0.0067λ(λ=632.8nm)。
Figure 6. a—sketch of adhesive position d1 and bipod apex height d2 b—influence of bipod apex on reflector
-
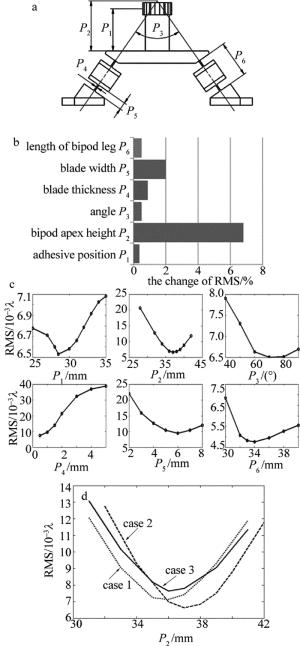
本文中结构设计过程中利用UG与ANSYS Work-bench接口传递设计变量，双向刷新模型，有效地提高了设计效率。主要设计变量如图 7a所示，包括两部分：一是双脚架结构相关的粘接位置P1、支撑脚延长线交点位置P2、支撑脚长度P6、支撑脚张角P3; 二是柔性铰链相关的柔节厚度P4、柔节长度P5。设置接口后, 在仿真软件中修改参量达到迅速变更模型的目的。分别控制一个设计变量改变，其它设计变量不变，分析各个参量单位变化对面形精度的影响, 如图 7b所示，图中横坐标表示参量单位变化引起的RMS值变化，体现了调整该参量来提高面型精度的有效程度。由图可知，支撑脚延长线交点位置P2对面形精度的影响较大，柔节宽度和柔节厚度参量影响次之。得到各个参量对面形精度的影响曲线，如图 7c所示。由图可知，在设计范围内柔节厚度P4对面形精度的影响呈单调关系，需要考虑结构刚度和强度条件以得到合适设计值；其它参量均存在局部最优解。任意选择3组其它参量组合情况下，分析得到P2的RMS曲线形状, 如图 7d所示，其曲线与图 7c中P2的RMS曲线类似，极值位置略有改变，总体规律一致。
Figure 7. a—sketch of design b—sensitivity of RMS with respect to the different dimensional parameters of mirror and flexure c—influence of individual parameter on RMS d—influence of P2 on RMS with different cases
-
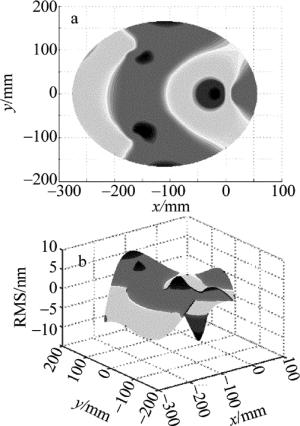
ULE反射镜为球面镜，曲率半径为1697mm。有限元模型采用六面体单元为主、四面体单元为辅的方式划分网格，共407810个节点，247262个单元。振动板底面施加固定约束，1g重力垂直光轴方向。首先通过MATLAB程序，利用齐次坐标转换法去除刚体位移，然后对变形前后的镜面面形进行拟合，得到变形前后的两个镜面面形曲面，最后计算得到沿光轴方向的面形误差, 如图 8所示。以RMS值为优化目标，得到最后优化结果, RMS为3.68nm，满足设计要求。
Figure 8. Analysis of surface figure distortion
-
发射环境对航天结构的影响最大，其影响包括横向载荷、瞬态载荷、冲击、稳态加速度等，对结构有刚度要求，反射镜组件的1阶固有频率应高于100Hz。对组件进行模态分析，背板底面做固定约束，得到1阶~6阶的模态, 如图 9所示, 对应频率如表 2所示。其1阶频率为123.41Hz满足设计要求。
Figure 9. Modal analysis of different orders
Table 2. Frequencies of different orders
modal 1 2 3 4 5 6 frequency/Hz 123.41 194.31 222.38 245.77 315.12 369.99 -
反射镜支撑背板要求刚度大、重量轻、材料热膨胀系数小。由于背板尺寸通常接近反射镜尺寸量级，热变形明显，对反射镜面形有较大的影响。本文中针对不同背板材料进行了热力学分析，以光学校核温度22℃为基准进行变温，考察满足面形精度RMS小于12.7nm(λ/50, λ=632.8nm)时的温度范围，材料属性和温度适宜范围对比见表 3。结果表明，基于工程应用的考量，该背部双脚架柔性支撑结构温度适应性良好，背板材料选择范围大，实际可根据温度适应性需求、结构重量需求以及经费因素等方面综合考虑选择合适材料。例如采用4J32材料，对结构整体施加4℃升温后，反射镜面形精度RMS为4.218nm，面形精度下降较小，RMS变化小于0.6nm。
Table 3. Comparison of back board material properties and thermal adaptability
material density ρ/(103kg·m-3) expenses range of temperature T/℃ aluminum alloy 2.80 low ±8 HT8 2.88 high ±16 TC4 4.43 medium ±17 4J32 8.13 high ±37 -
分析了双脚架支撑结构理论模型，从自由度角度阐述了双脚架支撑结构的优势。通常认为引入柔性铰链可以达到释放应力的目的，其本质是增加了空间机构自由度，但针对传统背部3点支撑，部分增加柔性铰链并不能达到静定约束的目的。相比之下，双脚架支撑结构结合柔性铰链实现了准静定约束，更具有提高面形精度的空间。
本文中针对中型反射镜提出了一种背部双脚架支撑方式，采用支撑脚延长线交点位置作为关键设计参量，利用参量化建模方法，完成了柔性支撑结构的设计与优化，并进行了相应的有限元分析。分析结果显示，该背部双脚架柔性支撑结构能够有效地释放热变形带来的附加载荷，温度适应性良好。优化设计后反射镜面形精度RMS为3.68nm，组件1阶频率达123.41Hz，满足设计要求。
空间反射镜背部双脚架柔性支撑结构设计
Structure design of backside bipod flexure mount for space reflector
-
摘要: 为了满足空间反射镜温度适应性好、结构紧凑的要求，采用有限元分析方法，以超低膨胀系数玻璃空间反射镜（Ø355mm）为支撑对象，设计了一种背部双脚架柔性支撑结构。首先研究了双脚架支撑的基本设计原则，从自由度角度分析了双脚架支撑结构相对背部3点支撑结构的优势。然后针对支撑结构尺寸参量、柔性铰链结构尺寸参量对面型精度的影响进行了仿真分析和优化设计，提出支撑脚延长线交点位置应作为背部双脚架支撑的关键设计参量，与粘接位置分别设计。结果表明，优化设计后的背部双脚架柔性支撑结构温度适应性好，能够有效卸载温度变化引入的附加载荷，同时具有较好的支撑效果和动态刚度；反射镜支撑后面形精度均方根值为3.68nm，组件的1阶频率达到123.41Hz，满足设计要求。该研究对未来背部双脚架支撑结构设计具有借鉴意义。Abstract: To satisfy the requirement of thermal adaptability and limited space, a kind of bipod flexure mounts for space reflector (Ø355mm) made of super low expansion coefficient glass was designed by finite element analysis (FEA) method. Firstly, the basic design principles of bipod flexure were studied. The advantage of bipod structure, compared with three points backside structure, was discussed from the view of freedom. Secondly, simulation analysis and optimization design were carried out for the influence of dimension parameters of support structure and flexure hinge on the surface figure accuracy. The intersection position of supporting foot extension line should be the key design parameters and the bonding position should be designed respectively. The results indicate that backside bipod flexure mounts after improved design has fine thermal adaptability and can effectively discharge the load caused by thermal variation, and has fine supporting ability and dynamic stiffness at the same time. root mean square of surface figure accuracy reaches 3.68nm, after reflection mirror mounting, and the first order frequency of assembly is 123.41Hz. The data can meet the design requirements. This study can supply the meaningful reference for future structure design of backside bipod mounts.
-
Key words:
- optical design /
- bipod flexible mount /
- finite element analysis /
- space reflector
-
Figure 1. Theoretical models of two types of mount
a—bipod mount b—three points backside mount
Figure 6. a—sketch of adhesive position d1 and bipod apex height d2 b—influence of bipod apex on reflector
Figure 7. a—sketch of design b—sensitivity of RMS with respect to the different dimensional parameters of mirror and flexure c—influence of individual parameter on RMS d—influence of P2 on RMS with different cases
Table 1. Material properties of primary mirror components
materials density ρ/(103kg·m-3) Young’s modulus E/GPa yield strength σs/MPa Poisson’s ratio μ CTE α/10-6K-1 TC4 4.43 109 860 0.31 8.8 4J32 8.13 148 276 0.29 0.31 ULE 2.210 67 — 0.17 0.015 
下载: 导出CSV
Table 2. Frequencies of different orders
modal 1 2 3 4 5 6 frequency/Hz 123.41 194.31 222.38 245.77 315.12 369.99
下载: 导出CSV
Table 3. Comparison of back board material properties and thermal adaptability
material density ρ/(103kg·m-3) expenses range of temperature T/℃ aluminum alloy 2.80 low ±8 HT8 2.88 high ±16 TC4 4.43 medium ±17 4J32 8.13 high ±37
下载: 导出CSV
-
[1] KIM H Y, YANG H S, MOON I K, et al. Adjustable bipod flexures for mounting mirrors in a space telescope[J]. Applied Optics, 2012, 51(32):7776-7783. doi: 10.1364/AO.51.007776 [2] LI Ch, HE X. Design of lightweight large aperture mirrors and supporting structures[J]. Laser Technology, 2015, 39(3):337-340(in Chinese). [3] OUAKNINE J, VIARD T, NAPIERALA B, et al. The FCI onboard MTG: opticaldesignand performances[C]//International Conference on Space Optics.New York, USA: SPIE, 2014: 10. [4] BIRKMANN S M, FERRUIT P, de OLIVEIRA C A, et al. Status of the JWST/NIRSpec instrument[C]//SPIE Astronomical Telescopes+Instrumentation.New York, USA: International Society for Optics and Photonics, 2014: 914308. [5] ZHANG L M, WANG F G, AN Q Ch, et al. Application of bipod to supporting structure of minitype reflector[J]. Optics and Precision Engineering, 2015, 23(2):438-443(in Chinese). doi: 10.3788/OPE. [6] DONG J H. Ball hinge support design and analysis for large aperture optical mirror[J]. OME Information, 2010, 27(9):29-34(in Chinese). [7] HUANG Zh. Advanced kinematics and dynamics of mechanisms[M]. Beijing:Higher Education Press, 2014:119-121(in Chinese). [8] LIAN H D, JIN J G, GONG H. Study of bipod structure design for space mirror[C]//23rd National Conference on Space Detection.Beijing: Chinese Society of Space Research, 2010: 79(in Chinese). [9] LIU T, ZHOU Y M, JIANG Y S. Research and application of foreign space mirror materials[J]. Spacecraft Recovery and Remote Sensing, 2013, 34(5):90-99(in Chinese). [10] YU J J, PEI X, BI Sh Sh, et al. State-of-arts of design method for flexure mechanisms[J]. Journal of Mechanical Engineering, 2010, 46(13):2-13(in Chinese). doi: 10.3901/JME.2010.13.002 [11] HATHEWAY A A E. Comparing blade and notch types of flexures[J]. Proceedings of the SPIE, 1997, 3132:290179. -
点击查看大图
图(9) / 表(3)
计量
- 文章访问数: 5688
- HTML全文浏览量: 3835
- PDF下载量: 292
- 被引次数: 0
