网站地图
-
直升机飞行的特点是能够垂直起降、在空中悬停、可以沿任意方向飞行，特别是可以高效、快速应对医疗救援、消防灭火、抢险救灾等紧急事件的救援活动，正是由于这些特点使其具有广阔的用途及发展前景。
随着低空开放试点在2015年全面推开，直升机执行救援任务将会越来越多，发生飞行事故的机率也会越来越大。通过对大量的飞行事故原因进行统计分析，发现进场着陆是安全飞行的关键阶段，也是事故发生的最多阶段，如何保证直升机的安全降落成为了社会关注的焦点[1]。目前，直升机辅助起降技术主要采用摄像系统、激光、毫米波雷达、红外线等技术，其中摄像系统技术价格较贵，激光、毫米波雷达技术的成本很高，红外线技术受环境影响比较大。
无线紫外光辅助起降技术利用紫外光的散射特性引导直升机进行安全降落，可以满足各种复杂环境下直升机应急起降的需求。由于无线紫外光波长较短，在传输过程中容易受到大气颗粒物的散射作用，使得传播路径可以绕过障碍物实现非直视通信，克服了其它光通信系统必须以直视方式工作的不足，且具有全天候工作、背景噪声小、抗干扰能力强等优点[2]。因此，无线紫外光通信在直升机辅助起降技术得到了广泛的应用[3-4]。
目前，紫外光通信系统普遍采用强度调制/直接检测系统，主要调制方式为开关键控(on-off keying, OOK)、脉冲位置调制(pulse position modulation, PPM)。其中，OOK在传输过程中容易受到大气湍流的影响，造成误比特率的增大，严重影响整个系统的性能[5-7]。与OOK相比，PPM具有较好的抗干扰能力以及较高的功率利用率。近几年，国内外有大量文献研究大气湍流对光通信影响[6-13]，但大多侧重于激光通信，在紫外光非直视通信方面，涉及的文献比较少。已有学者研究了弱湍流条件下紫外光OOK调制的误码性能，却很少有人研究大气湍流中PPM对紫外光非直视通信误码性能的影响。作者基于直升机助降紫外光非直视通信模型，理论推导了弱湍流条件下OOK，PPM的误比特率，并且仿真分析了OOK，4-PPM，8-PPM，16-PPM在不同条件下的误码性能。
-
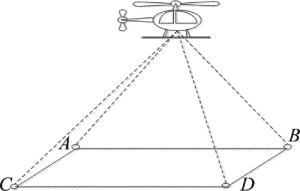
紫外光引导直升机助降模型如图 1所示。直升机降落区域的4个顶点A，B，C，D分别放置250nm，255nm，260nm，265nm紫外发光二极管(light emitting diode, LED)发射装置，接收装置悬挂在直升机底部。当直升机到达降落地点上空后，发射装置将降落区域的温湿度、风速、大气压强等环境信息通过紫外LED发射出去。接收装置通过对探测到的信号进行处理，得到直升机与降落区域之间的距离以及相关环境信息，并将最终结果呈现在显示器上。飞行员根据得到的相关信息，调整直升机的姿态，判断最佳着陆地点，操纵直升机安全降落。
Figure 1. Helicopter landing model using ultraviolet guiding technology
紫外光引导直升机助降主要包括以下3个阶段：(1)发射端布置阶段。地面工作人员首先将紫外LED发射装置安装在直升机降落区域的4个顶点，然后进行紫外LED光源调试和校准工作，检查紫外LED发射装置是否正常工作，为直升机的降落做好准备工作; (2)直升机搜索降落区域阶段。当直升机进入降落区域附近上空时，飞行员根据直升机上接收装置收到的信息，不断调整直升机的飞行方向，到达指定降落区域的上空; (3)直升机降落阶段。当直升机准备降落时，发射装置不间断将降落区域的温湿度、风速、风向等环境信息发送给直升机并提供给飞行员，飞行员根据地面实际降落情况，不断调整直升机的姿态，操纵直升机安全降落。
-
直升机助降紫外光通信过程中，受到的影响主要有大气分子的吸收与散射以及大气湍流引起的湍流效应。其中大气湍流使得接收到的紫外光信号受到严重干扰，导致误比特率增加，对紫外光通信性能的影响非常大。同时由于紫外光引导直升机助降过程中，大部分情况下降落区域4个顶点处的发射装置与接收装置非共面，只能与直升机进行非直视通信。因此本文中基于直升机助降紫外光非直视通信模型，分析了弱湍流条件下OOK和PPM对紫外光通信性能的影响。
-
对于局地均匀各向同性的湍流，通常用结构常数Cn2表征大气湍流的强弱。大气湍流结构常数Cn2模型很多，最著名的是修正Hufnagel-Valley(HV)模型：
$ \begin{array}{*{20}{c}} {C_n^2\left( h \right) = 8.16 \times {{10}^{ - 54}}{h^{10}}{{\rm{e}}^{ - h/1000}} + 3.02 \times }\\ {{{10}^{ - 17}}{{\rm{e}}^{ - h/1500}} + 1.90 \times {{10}^{ - 15}}{{\rm{e}}^{ - h/100}}} \end{array} $
(1) 式中，h表示海拔高度(单位为m)。一般而言，近地面处Cn2的典型值从10-12m-2/3(强湍流)~10-18m-2/3(弱湍流)。由于大气湍流的强弱与大气对流的强弱密切相关，而随着海拔高度的增加，大气湍流的强度随之减弱，大气湍流结构常数Cn2随之减弱。总之，Cn2不仅与海拔高度有关，还与温度的变化有关，并随着天气、季节以及地理环境的不同而不断变化。
-
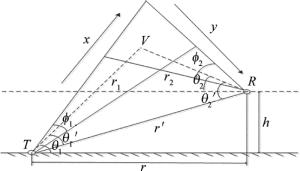
在大气环境下，直升机助降下无线紫外光非直视通信链路模型如图 2所示。如果以发送端T与接收端R所在的平面为参考面，φ1为发散角，φ2为接收视场角，θ1为发送仰角，θ2为接收仰角，V为有效散射体区域，r′是发送端到接收端的基线距离，r1和r2分别为发送端和接收端到有效散射体的距离。如果以地面为参考面，收发端的水平距离差为r，接收端R距离地面的高度为h，由于发送端T与接收端R处在不同高度，二者的基线距离为$r' = \sqrt {{r^2} + {h^2}} $。此时的发射仰角θ1与接收仰角θ1分别变成了图中的θ1′与θ2′[14]。
Figure 2. Wireless ultraviolet non-line-of-sight communication link model
紫外光非直视通信传输路径被分成2个直视链路，其中一条从发射端到达共同散射体的路径为x路径，传输距离r1，另一条是从共同散射体到达接收端为y路径，传输距离为r2。
ix和ix′分别是在湍流条件下发射端到达散射体的信号强度和平均信号强度，为了方便计算，本文中均令ix′=1。iy和iy′分别是在湍流条件下散射体到接收端的信号强度和平均信号强度，iy′表示为：
$ {{i'}_y} = {i_x}A{P_{\rm{s}}}\frac{{{K_{\rm{s}}}}}{{4{\rm{ \mathsf{ π} }}}}\frac{{\exp \left( { - {K_{\rm{a}}}{r_2}} \right)}}{{r_2^2}} $
(2) 式中，A是有效接收孔径面积，Ps是散射相函数，Ka是衰减系数，Ks是散射系数。
弱湍流条件下紫外光的信号强度起伏服从对数正态分布，其概率密度函数为[15]：
$ f\left( I \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}{\sigma ^2}I} }}\exp \left[ { - {{\left( {\ln I + \frac{{{\sigma ^2}}}{2}} \right)}^2}/\left( {2{\sigma ^2}} \right)} \right] $
(3) 式中，I表示紫外光接收的光强。采用Kolmogorov折射率起伏功率谱，非直视传输的闪烁指数为：
$ {\sigma ^2} = {{\rm{e}}^{4\sigma _{\rm{a}}^2}} - 1 \approx 4\sigma _{\rm{a}}^2 $
(4) 式中，σa2为对数振幅起伏方差, 斜程传输时，对于平面波[16]有：
$ \sigma _{\rm{a}}^2 = 0.56{k^{7/6}}{\left[ {\sec \varphi } \right]^{11/6}}\int_0^L {C_n^2\left( l \right){{\left( {L - l} \right)}^{5/6}}{\rm{d}}l} $
(5) 式中, $k = \frac{{2\pi }}{\lambda }$，λ为紫外光波长，φ为天顶角(φ＜60°)，secφ是对非直视路径的修正因子, Cn2是大气湍流结构常数，L是传播路径长度，在x路径上为r1, 在y路径上为r2, l表示紫外光传播距离。
结合(3)式、(4)式和(5)式，可分别得到x路径、y路径的闪烁指数和归一化信号强度概率密度函数以及接收端归一化信号强度边缘分布概率密度函数[17]。
-
弱湍流信道下, 对于光强度调制通信系统, 接收端经过光电转换后，得到的电信号y(t)可以表示为：
$ y\left( t \right) = \eta Dz\left( t \right)X\left( t \right) + n\left( t \right) $
(6) 式中, η为收发天线的合并光效率, D为光电响应度，z(t)表示大气信道状态，X(t)为发射的光强信号，n(t)为加性高斯白噪声。
在无湍流的高斯信道下，采用OOK和PPM调制方式时的误比特率分别为[18]：
$ {P_{{\rm{OOK}}}} = \frac{1}{2}{\rm{erfc}}\left( {\eta DP\sqrt {\frac{1}{{2\sigma _{\rm{n}}^2}}} } \right) $
(7) $ {P_{{\rm{PPM}}}} = \frac{{\rm{L}}}{4}{\rm{erfc}}\left( {\eta DP\sqrt {\frac{{L\lg \left( {2L} \right)}}{{2\sigma _{\rm{n}}^2}}} } \right) $
(8) 式中, P是平均发射功率，σn2是加性高斯白噪声方差，erfc(·)是互补误差函数。
则弱湍流条件下OOK和PPM调制方式时的误比特率分别为：
$ {P_{{\rm{OOK}}}}\left( e \right) = \int_0^\infty {p\left( u \right)\frac{1}{2}{\rm{erfc}}\left( {\eta DPu\sqrt {\frac{1}{{2\sigma _{\rm{n}}^2}}} } \right){\rm{d}}u} $
(9) $ {P_{{\rm{PPM}}}}\left( e \right) = \int_0^\infty {p\left( u \right)\frac{L}{4}{\rm{erfc}}\left( {\eta DPu\sqrt {\frac{{L\lg \left( {2L} \right)}}{{2\sigma _{\rm{n}}^2}}} } \right){\rm{d}}u} $
(10) 式中, p(u)为接收端归一化信号强度边缘分布概率密度函数, u为接收端归一化信号强度。
-
根据上述理论分析，仿真分析了在弱湍流(Cn2=1.4×10-17m-2/3)条件下系统参量(发射功率、通信距离、发散角、视场角、收发仰角)对紫外光非直视通信的误码性能的影响，仿真过程中，部分系统参量取值如表 1所示。
Table 1. Some simulation parameters of system
parameter value receiving aperture area A 1.77cm2 wavelength λ 250nm attenuation coefficient Ka 1.961×10-3 scattering coefficient Ks 0.759×10-3 scattering phase function Ps 1 photoelectric response D 48mA/W 图 3中仿真分析了在OOK, PPM调制方式下发射功率、通信距离对误比特率RBER的影响。其中发散角ϕ1=10°，视场角ϕ2=30°，收发仰角θ1=θ2=20°，数据传输速率Rt=100kbit/s，图 3a中的通信距离r=200m，图 3b中的发射功率Pt=20mW。从图 3a可以看出，不同调制方式的误比特率随着发射功率的增大而逐渐减小，在相同误比特率条件下，PPM比OOK需要更少的发射功率。当误比特率为10－6时，4-PPM, 8-PPM, 16-PPM分别比OOK节省了12mW, 19mW, 24mW的发射功率。从图 3b可以看出，不同调制方式的误比特率随着通信距离的增大而逐渐增大，在相同误比特率条件下，PPM比OOK传输的距离更远。当误比特率为10－6时，4-PPM, 8-PPM, 16-PPM分别比OOK多了53m, 102m, 183m的通信距离。
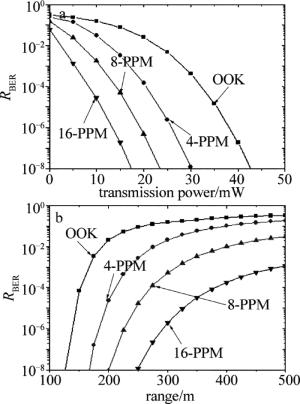
Figure 3. a—effect of transmission power on BER for OOK and PPM b—effect of range on BER for OOK and PPM
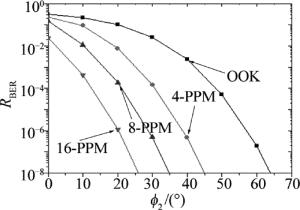
表 2和图 4中仿真分析了在OOK, PPM调制方式下发散角、视场角对误比特率RBER的影响。其中收发仰角θ1=θ2=20°，发射功率Pt=15mW，通信距离为r=200m，数据传输速率Rt=100kbit/s，表 2中的视场角ϕ2=30°，图 4中的发散角为ϕ1=10°。从表 2可以看出，不同调制方式的误比特率随着散射角的增大而逐渐减小，散射角对误比特率的影响很小。在相同散射角条件下，PPM比OOK的误比特率更低。从图 4可以看出，不同调制方式的误比特率随着视场角的增大而逐渐减小。在相同视场角条件下，PPM比OOK的误比特率更低。当视场角小于40°时，误比特率变化很小；当视场角大于40°时，误比特率变化比较明显。
Table 2. Effect of ϕ1 on RBER for OOK and PPM
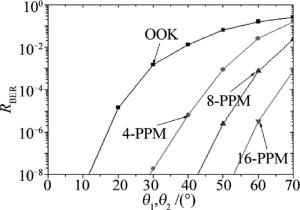
ϕ1 modulation OOK 4-PPM 8-PPM 16-PPM 10° 7.72×10-2 3.30×10-3 5.04×10-5 1.86×10-7 20° 7.68×10-2 3.20×10-3 4.92×10-5 1.80×10-7 30° 7.62×10-2 3.10×10-3 4.73×10-5 1.70×10-7 40° 7.53×10-2 3.00×10-3 4.48×10-5 1.58×10-7 50° 7.41×10-2 2.90×10-3 4.17×10-5 1.43×10-7 60° 7.27×10-2 2.70×10-3 3.81×10-5 1.27×10-7 70° 7.10×10-2 2.60×10-3 3.43×10-5 1.10×10-7 
Figure 4. Effect of ϕ2 on RBER for OOK and PPM
图 5中仿真分析了在OOK, PPM调制方式下收发仰角对误比特率的影响。其中发散角ϕ1=10°，视场角ϕ2=30°，发射功率Pt=15mW, 数据传输速率Rt=50kbit/s，通信距离r=200m。从图 5可以看出，不同调制方式的误比特率随着收发仰角的增大而逐渐减小。在相同收发仰角条件下，PPM比OOK的误比特率更低；当收发仰角小于40°时，误比特率变化比较大；当收发仰角大于40°时，误比特率变化比较小。
Figure 5. Effect of θ1 and θ2 on RBER for OOK and PPM
-
基于直升机助降紫外光非直视通信模型，对弱湍流环境下紫外光通信系统的误比特率进行了研究，推导了OOK, PPM调制方式的误比特率，并以此为理论基础进行了仿真分析。结果表明，在相同条件下，PPM比OOK需要的发射功率更少、传输的距离更远、误比特率更低。在紫外光通信过程中，发散角对误比特率影响不大，使用大角度视场角和小角度收发仰角能够极大提高误码性能。无线紫外光在大气湍流传输过程中，高阶PPM比OOK具有更大的优势。这为继续研究直升机助降无线紫外光通信系统性能的相关人员提供一定的参考。
大气湍流中直升机助降紫外光引导调制研究
Modulation research of helicopter landing using ultraviolet guiding technology in atmospheric turbulence
-
摘要: 为了研究大气湍流中不同调制方式对无线紫外光通信系统的性能影响，基于紫外光非直视通信模型，理论推导了弱湍流条件下开关键控、脉冲位置调制的误比特率。采用紫外光引导直升机助降模型，在不同调制方式下仿真分析了发射功率、通信距离、发散角、接收视场角、收发仰角对误比特率的影响。结果表明，不同调制方式的误比特率随着发射功率、发散角、接收视场角的增大而不断减小，随着通信距离、收发仰角的增大而增大; 在相同条件下，脉冲位置调制比开关键控的误比特率更低，而且随着调制阶数的增加，误比特率会越来越小。这一结果对提高紫外光通信系统在大气湍流中的抗干扰能力具有一定的应用价值。Abstract: In order to study effect of different modulations on performance of wireless ultraviolet(UV) communication systems in atmospheric turbulence, the expressions of bit error rate (BER) using on-off keying(OOK) and pulse position modulation (PPM) based on UV non-line-of-sight(NLOS) communication model in weak turbulence were derived. Helicopter landing model using UV guiding technology was introduced and effect of transmission power, range, transmitter (Tx) beam divergence, receiver (Rx) field of view (FOV), Tx and Rx elevation angle on BER under different modulations were simulated. The results show that BER under different modulations decreases with the increase of transmitted power, Tx beam angle and Rx FOV, while increases with the increase of range, Tx and Rx elevation angle. Under the same condition, PPM has a better BER performance than OOK. BER decreases with the increasing of modulation order. The results have applicable values for improving the jamming-rejection capability of ultraviolet communication systems in atmospheric turbulence.
-
Figure 3. a—effect of transmission power on BER for OOK and PPM b—effect of range on BER for OOK and PPM
Table 1. Some simulation parameters of system
parameter value receiving aperture area A 1.77cm2 wavelength λ 250nm attenuation coefficient Ka 1.961×10-3 scattering coefficient Ks 0.759×10-3 scattering phase function Ps 1 photoelectric response D 48mA/W 
下载: 导出CSV
Table 2. Effect of ϕ1 on RBER for OOK and PPM
ϕ1 modulation OOK 4-PPM 8-PPM 16-PPM 10° 7.72×10-2 3.30×10-3 5.04×10-5 1.86×10-7 20° 7.68×10-2 3.20×10-3 4.92×10-5 1.80×10-7 30° 7.62×10-2 3.10×10-3 4.73×10-5 1.70×10-7 40° 7.53×10-2 3.00×10-3 4.48×10-5 1.58×10-7 50° 7.41×10-2 2.90×10-3 4.17×10-5 1.43×10-7 60° 7.27×10-2 2.70×10-3 3.81×10-5 1.27×10-7 70° 7.10×10-2 2.60×10-3 3.43×10-5 1.10×10-7
下载: 导出CSV
-
[1] LIU S B, SHI P A, CHEN J H. Analysis and evaluation of ship-based helicopter take-off and landing safety[J].Ship Electronic Engineering, 2014, 34(2):106-109 (in Chinese). [2] ELSHIMY M A, HRANILOVIC S. Binary-input non-line-of-sight solar-blind UV channels: modeling, capacity and coding [J]. Optical Communications & Networking, 2012, 4(12):1008-1017. [3] ZHAO T F, WU P F, SONG P. Research on the wireless ultraviolet communication technology in helicopter launching and landing guidance [J]. Laser Journal, 2014, 35(10):9-13 (in Chinese). [4] ZHAO T F, LIU X, LOU J P. Research on wireless ultraviolet guiding fountain code technology of helicopter emergency landing[J]. Journal of Electronics & Information Technology, 2015, 37(10):2052-2059 (in Chinese). [5] XU S H, XIAO S L, WANG S, et al. Research on modulating retro-reflector technology of laser communication systems based on acousto-optic modulation[J]. Laser Journal, 2015, 39(5): 598-602(in Chinese). [6] CHEN D, KE X Zh. Analysis on error rate of wireless optical communication using subcarrier modulation on LDPC code [J]. Laser Journal, 2011, 35(2):389-402 (in Chinese). [7] YI M, LI T S, CHEN M S, et al. Frame synchronization for multi-pulse position modulation in optical communication[J]. Laser Journal, 2010, 34(2):164-167 (in Chinese). [8] ZUO Y, XIAO H F, WU J, et al. Closed-form path loss model of non-line-of-sight ultraviolet single-scatter propagation[J]. Optics Letters, 2013, 38(12): 2116-2118. doi: 10.1364/OL.38.002116 [9] JU M G, YUE P, LIU Z J, et al. BER performance for multi-level pulse position modulation over Gamma-Gamma turbulence channel[J].Journal of Optoelectronics·Laser, 2013, 24(9):1702-1707 (in Chinese). [10] JI Y, YUE P, YAN R Q, et al. BER performance analysis of the atmospheric laser communication system on the slant path in weak turbulence[J].Journal of Xidian University, 2016, 43(1):66-70 (in Chinese). [11] LIU Y, ZHANG G A. Performance analysis of an indoor LDPC coded FSO communication system under weak turbulent condition[J].Laser Technology, 2015, 39(3):410-415 (in Chinese). [12] WANG R Y, LIU F H, LI X Y.Design of BER measurement system for UV communication [J]. Semiconductor Optoelectronics, 2012, 33(5):707-710 (in Chinese). [13] WANG D F, CHU Z F, REN Z L, et al. Influence of atmospheric turbulence on BER of laser communication system[J]. Laser & Infrared, 2011, 41(4):390-393(in Chinese). [14] HE H, KE X Zh, ZHAO T F. Research of NLOS ultraviolet single scattering link model with height information[J]. Laser Technology, 2011, 35(4): 495-498(in Chinese). [15] WANG Y, YU L, CAO J N. Performance of optical wireless communication system basing on the sub-carrier PSK intensity modulation and LDPC code[J]. Acta Optica Sinica, 2009, 29(12):3295-3298(in Chinese). doi: 10.3788/AOS [16] LI X F. The principle and technology of the satellite-to-ground laser communication links[M].Beijing: National Defense Industry Press, 2011:32-57(in Chinese). [17] QIANG R X, ZHAO S H, WANG X, et al. Influence of high atmosphere turbulence on Scintillation in non-line-of-sight ultraviolet channel[J]. Semiconductor Optoelectronics, 2014, 35(4):677-681(in Chinese). [18] HRANILIVIC S. Wireless optical communication systems [M]. New York, USA:Springer, 2005:71-78. -
点击查看大图
图(5) / 表(2)
计量
- 文章访问数: 8042
- HTML全文浏览量: 5976
- PDF下载量: 16
- 被引次数: 0
