网站地图
下载:
-
随着计算机处理速度的提高以及电荷耦合器件(charge-coupled device，CCD)的问世，数字全息已经成为一个十分活跃的研究领域[1-10]。数字全息技术使用CCD记录数字全息图，通过衍射的数值计算在计算机的虚拟空间重建物光场的波前。常用的两种波前重建算法是基于菲涅耳衍射的一次傅里叶变换法和基于角谱衍射理论的两次傅立叶变换法[11-12]。在通常的实验验证过程中，在使用这两种方法进行波前重建时，再现距离通常取物平面到全息面的测量距离，并未考虑物光波在不同介质中传播时对测量距离的影响。一般情况下，这种计算是基本准确的，但在一些特殊的应用场合，如要求高分辨成像，或物光波通过其它介质距离较长时，其影响将不能被忽略。如在显微数字全息中，3维洋葱细胞通常放置在液体介质中进行检测，显然，倘若还是采用测量距离值作为再现距离进行波前重建，并不能得到正确的重建结果。
通过对数字全息系统焦深[13]的分析得知，只要在系统焦深范围内进行数字全息波前重建，都可得到准确的像面结果，当重建距离超出数字全息系统的焦深范围时，需要分析影响系统准确重建距离的因素。本文中通过对物光波通过非单一介质后对重建距离的影响进行了实验研究。研究表明，物光波通过常用分束镜时引起了重建距离的变化，使得重建距离超出了数字全息重建图像的焦深范围。因而，直接采用测量距离作为再现距离进行波前重建通常都不能得到清晰的再现像。本文中将光波在介质中传播时的波长转换为等效波长，进而计算出等效的重建距离，采用等效距离对全息图波前重建公式进行修正，得到准确的计算结果，并与傍轴近似的柯林斯公式计算结果[14-17]进行比较。结果表明：使用等效距离修正的重建公式，能简便地实现数字全息波面的准确重建计算。研究结果可为显微数字全息及数字全息检测应用提供有益的参考。
-
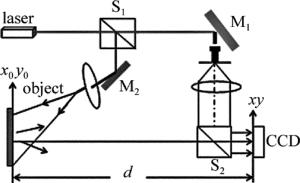
数字全息记录的简图如图 1所示。x0y0为物平面，激光自左向右被分束镜S1分为两束光，其中由S1透射的光经过全反射镜M1反射，由准直扩束后投向分束镜S2，经过S2反射的光波到形成参考光。通过S1反射的光波经过反射及扩束以后形成照明光投射向物体，从物体表面散射的光波通过半反半透镜S2到达CCD形成物光。两束光干涉后由CCD记录得到全息图，计算机上进行实时采集存储，然后在计算机上对数字全息图进行重建。重建时可使用下面两种算法进行。
Figure 1. Experiment configuration for digital holography recording
-
设到达CCD的物光波和参考光波的复振幅分别为O和R，则记录的光强Ih可以表示为：
$ {I_{\rm{h}}} = {\left| O \right|^2} + {\left| R \right|^2} + {O^*}R + O{R^*} $
(1) 物体到CCD的距离为d，重建光波为单位振幅的平面波，使用重建光波照明全息图后的透射光波经过距离为d的衍射后，在满足傍轴近似的条件下，再现光场复振幅分布为：
$ \begin{array}{l} U({x_{\rm{o}}}, {y_{\rm{o}}}) = \frac{{\exp \left( {{\rm{j}}kd} \right)}}{{{\rm{j}}\lambda d}}\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {{I_{\rm{h}}}(x, y)} } \times \\ \exp \left\{ {\frac{{{\rm{j}}k}}{{\lambda d}}\left[ {{{({x_{\rm{o}}} - x)}^2} + {{({y_{\rm{o}}} - y)}^2}} \right]} \right\}{\rm{d}}x{\rm{d}}y \end{array} $
(2) 式中，λ为波长，波数k=2π/λ，${\rm{j}} = \sqrt { - 1} $，xy和xoyo分别为全息面坐标系和重建像面坐标系。设CCD的尺寸为Lx×Ly，像素数为M×N，则取样间距Δx=Lx/M，Δy=Ly/N。(2)式可用快速傅里叶变换(fast Fourier transform，FFT)表示为：
$ \begin{array}{l} \;\;\;\;\;\;\;\;U(p\Delta {x_{\rm{o}}}, q\Delta {y_{\rm{o}}}) = \frac{{\exp \left( {{\rm{j}}kd} \right)}}{{{\rm{j}}\lambda d}} \times \\ \;\;\;\;\;\;\;\exp \left[ {\frac{{{\rm{j}}k}}{{2d}}{{(p\Delta {x_{\rm{o}}})}^2} + {{(q\Delta {y_{\rm{o}}})}^2}} \right] \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathscr{F}\left\{ {{I_{\rm{h}}}\left( {m\Delta x, n\Delta y} \right) \times } \right.{\rm{ }}\\ {\left. {\;\;\;\;\;\;\;\;\exp \left[ {\frac{{{\rm{j}}k}}{{2d}}\left( {{{\left( {m\Delta x} \right)}^2} + {{\left( {n\Delta y} \right)}^2}} \right)} \right]} \right\}_{\frac{{p\Delta {x_{\rm{o}}}}}{{\lambda d}}, \frac{{q\Delta {y_{\rm{o}}}}}{{\lambda d}}}}{\rm{, }}\\ \left( {p, m = - \frac{M}{2} \sim \frac{M}{2} - 1;q, n = - \frac{N}{2} \sim \frac{N}{2} - 1} \right) \end{array} $
(3) 式中，Ih(mΔx, nΔy)为全息面Ih(x, y)的离散形式，m和n为取样点对应的序号; Δxo和Δyo为离散傅里叶变换后空域的取样间隔，p和q为取样点对应的序号，根据Shannon采样定理，其取样间隔分别为$\Delta {x_{\rm{o}}} = \frac{{\lambda d}}{{M\Delta x}}, \Delta {y_{\rm{o}}} = \frac{{\lambda d}}{{N\Delta y}}$。
-
当采用照明光波C(x, y)照射全息图Ih(x, y)，出射光波的傅里叶变换可以表示为：
$ {G_0}({f_x}, {f_y}) = \mathscr{F}\left\{ {C(x, y){I_{\rm{h}}}(x, y)} \right\} $
(4) 根据角谱衍射理论，在离全息面距离为d的观察面，再现光场复振幅的离散形式为：
$ \begin{array}{l} U(p\Delta {x_{\rm{o}}}, q\Delta {y_{\rm{o}}}) = {\mathscr{F}^{ - 1}}\left\{ {{G_0}(m\Delta {f_x}, n\Delta {f_y}) \times } \right.\\ \left. {\exp \left[ {{\rm{j}}kd\sqrt {1 - {{(\lambda m\Delta {f_x})}^2} - {{(\lambda n\Delta {f_y})}^2}} } \right]} \right\}, \\ \left( {p, m = - \frac{M}{2}\sim \frac{M}{2} - 1;q, n = - \frac{N}{2}\sim \frac{N}{2} - 1} \right) \end{array} $
(5) 式中，${\mathscr{F}^{ - 1}}$表示快速傅里叶逆变换，频率的取样间隔Δfx=Lx－1, Δfy=Ly－1。
-
在实际实验系统中，重建距离通常取记录时物体到CCD的测量距离，下面给出常用系统的实验结果。实验物体为美国空军(United States Air Force, USAF)分辨率测试板，采用图 1的数字全息记录系统。实验研究中，照明光波波长λ=632nm，CCD的像元宽度为0.00465mm，总像素数N×N=1024×1024，对应尺寸为Lx×Ly=4.76mm×4.76mm。在通常的数字全息实验系统中，分束镜是必需的光学元件，故以分束镜为例研究介质空间对波面传播的影响，使用两种不同尺寸的分束镜进行实验研究。采用的分束镜光轴方向的厚度为75mm时，测得物体到CCD的距离d=200mm及d=150mm两组数据；当分束镜光轴方向的厚度为25.4mm时，测得物体到CCD的距离d=65mm，分束镜的折射率n=1.5。采用一次FFT和基于角谱衍射理论两次傅里叶变换法对数字全息图进行重建，图 2和图 3中分别给出再现距离为200mm, 150mm和65mm时的重建图像。观察可知，当光波在不同介质中传播时，对于不同记录距离的数字全息图，采用两种同波前重建算法对其进行再现时，均不能得到清晰的再现像。
Figure 2. Wavefront reconstruction based on fast Fourier transform
Figure 3. Wavefront reconstruction based on angular spectrum diffraction theory
-
当光在不同的介质中传播时，其改变的是光波的波长。当物光波在厚度为db分束镜中传播，相较于光在真空中传播，其相当于在距离为db的长度内填充折射率为n的介质。设光在真空、介质中传播的波长分别为λ和λ0，传播速率分别为c和v，则在介质中波长为：
$ {\lambda _0} = \frac{c}{{nv}} = \frac{\lambda }{n} $
(6) 对于菲涅耳积分表达式，将(6)式带入(2)式中，令物光波传播到分束镜入射面的复振幅为Ub(xb, yb)，出射面复振幅为U(xo, b, yo, b)，则光波介质中传播时的菲涅耳衍射积分为：
$ \begin{array}{l} U({x_{{\rm{o, b}}}}, {y_{{\rm{o, b}}}}) = \frac{{\exp ({\rm{j}}2{\rm{ \mathsf{ π} }}{d_{\rm{b}}}n/\lambda )}}{{{\rm{j}}\lambda {d_{\rm{b}}}/n}}\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {{U_{\rm{b}}}({x_{\rm{b}}}, {y_{\rm{b}}})} } \times {\rm{ }}\\ {\rm{exp}}\left\{ {\frac{{{\rm{j}}\pi }}{{\lambda {d_{\rm{b}}}/n}}\left[ {{{({x_{{\rm{o, b}}}} - {x_{\rm{b}}})}^2} + {{({y_{{\rm{o, b}}}} - {y_{\rm{b}}})}^2}} \right]} \right\}{\rm{d}}{x_{\rm{b}}}{\rm{d}}{y_{\rm{b}}} \end{array} $
(7) 对于图 1中数字全息记录系统，考虑到光波在折射率为n中传播时，将(7)式与(2)式对比可以知道，在分束镜中光波实际走过的距离为db/n，因而实际的距离de可以等效为：
$ {d_{\rm{e}}} = d - {d_{\rm{b}}} + \frac{{{d_{\rm{b}}}}}{n} $
(8) 即物光波在实际的介质中传播时的等效距离可以通过(8)式计算得到，当采用厚度为75mm和25.4mm的分束镜时，其计算得到对应的等效记录距离分别为de=175mm，de=125mm和de=56mm。采用一次FFT和基于角谱衍射理论的两次傅里叶变换法对数字全息图进行重建，结果如图 4和图 5所示。观察可知，采用等效距离重建数字全息图时，得到了比较清晰的再现像。与第1.3节中的重建结果比较知，由于分束镜厚度对重建距离的影响，使得实际的记录距离的光线的光程发生了变化，因而直接采用测量距离作为再现距离进行重建，并不能获得准确的重建像。
Figure 4. Wavefront reconstruction based on fast Fourier transform
Figure 5. Wavefront reconstruction based on angular spectrum diffraction theory
-
对于一次傅里叶变换系统的焦深范围，参考文献[13]中给出了详细的推导证明。根据文献中的研究，数字全息重建图像的系统焦深定义如下：
$ 2\left| {{z_a} - {z_i}} \right| \approx 3\frac{{\lambda {z_{\rm{i}}}^2}}{{{L^2}}} $
(9) 式中，za和zi分别是实际的再现距离和理想的成像距离。不难看出，随着理想像重建距离zi的增加，重建图像的系统焦深会增加；而随着全息图宽度的增加，系统焦深会随之下降。根据第2节中的结论，当再现距离为de=175mm，L取CCD的面尺寸，代入(9)式，|za－zi|=1.3mm，即重建时实际能成清晰像的系统焦深范围为(175±1.3)mm，显然，若采用200mm进行数字全息波前重建，已经超出了焦深范围，因而不能得到清晰的再现像。
-
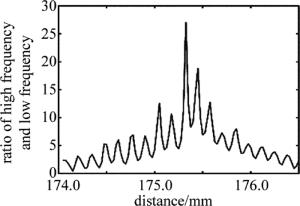
对于采用等效距离计算得到的重建图像, 如图 6所示。在一系列对图像清晰度的评价方法中，有一种方法是通过图像的高频与低频部分的比值来衡量重建像的清晰度，比值的最大值为图像最清晰处[18]。采用等效距离修改正后的公式对图像进行重建，对重建图像做傅里叶变换，将零级视为低频，其余部分视为高频，在系统的焦深范围内，采用自动聚焦的方式，对于不同记录距离的重建图像，其高频与低频的比值曲线如图 7所示。由分析可知，重建图像在175.3mm处有最大值，即此处成像是最清晰的位置，这与之前计算得到等效距离的值是基本一致的，因而采用等效距离修正后的公式能较好地成像。
Figure 6. Wavefront reconstruction based on equivalent distance
Figure 7. Ratio of high frequency and low frequency
-
物光波通过实际的光学系统时，通常采用柯林斯公式进行研究。光波通过介质时，轴对称傍轴光学系统可以由2×2的矩阵$\left[ {{array}{*{20}{c}} A&B\\ C&D {array}} \right]$描述[14]。设入射平面为全息面，出射平面为观察面，坐标分别由xy和xoyo表示。根据柯林斯建立的入射平面光波场Ih(x, y)与出射平面光波场U(xo, yo)的关系[15]，观察面复振幅的离散形式可以表示为：
$ \begin{array}{l} U(p\Delta {x_{\rm{o}}}, q\Delta {y_{\rm{o}}}) = \frac{{\exp \left( {{\rm{j}}k{L_{{\rm{axis}}}}} \right)}}{{{\rm{j}}\lambda B}} \times \\ \;\;\;\;\;\;\;\exp \left\{ {\frac{{{\rm{j}}kD}}{{2B}}\left[ {{{(p\Delta {x_{\rm{o}}})}^2} + {{(q\Delta {y_{\rm{o}}})}^2}} \right]} \right\} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathscr{F}\left\{ {{I_{\rm{h}}}\left( {m\Delta x, n\Delta y} \right) \times } \right.\\ {\left. {\;\;\;\;\;\;\;\;\exp \left[ {\frac{{{\rm{j}}kA}}{{2B}}\left( {{{\left( {m\Delta x} \right)}^2} + {{\left( {n\Delta y} \right)}^2}} \right)} \right]} \right\}_{{f_x} = \frac{{p\Delta {x_{\rm{o}}}}}{{\lambda B}}, {f_y} = \frac{{q\Delta {y_{\rm{o}}}}}{{\lambda B}}}}{\rm{, }}\\ \left( {p, q, m, n = - N/2, - N/2 - 1, \cdots , N/2 - 1} \right) \end{array} $
(10) 光传输矩阵中元素ABCD的值分别是A=1，$ - B = d - {d_{\rm{b}}} + \frac{{{d_{\rm{b}}}}}{n}$，C=0，D=1，Laxis为ABCD光学系统的轴上光程，N为CCD的像素数，L为CCD面尺寸，Lo为出射面光波场的空域宽度(即出射平面的尺寸)，Lo可以表示为：
$ {L_{\rm{o}}} = \frac{{N\lambda B}}{L} $
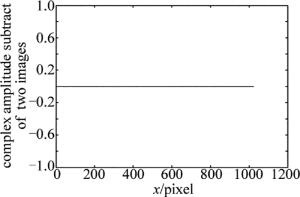
(11) 为便于讨论，选取记录距离d=200mm时的数字全息图进行重建, 图像如图 8所示。采用柯林斯公式重建像与采用等效距离修正后的公式进行波前重建像，取第30行的复振幅的值做差, 如图 9所示。从图 9中可知，光波通过不同尺寸的分束镜时，采用柯林斯公式和采用基于等效距离对数字全息图重建时有基本一致的结果。
Figure 8. Reconstruction based on Collins formula
Figure 9. Complex amplitude subtract of two reconstruction images in different method
-
当光波在非单一介质中传播时，给出了将记录距离等效为介质中传播距离的方法。结果表明，计算光波在介质中传播的等效距离，并采用等效距离对数字全息图进行波前重建的结果与采用柯林斯公式重建的结果是一致的。此方法相较于采用柯林斯公式对数字全息图进行波前重建更简单方便，期望此方法能对数字全息图的波前重建提供有益的参考。
数字全息波前准确重建的实验研究
Experiment research of accurate wavefront reconstruction of digital holography
-
摘要: 为了得到数字全息图波前的准确重建场，采用常见的波前重建算法进行实验研究和理论分析，得到了物光波通过非单一介质传播时的等效距离，并利用该等效距离修改常用波面重建公式中的相关参量，与柯林斯公式对数字全息图进行重建的结果进行比较分析，发现当物光波通过非单一介质时，采用等效距离修正的重建公式或者柯林斯公式均能得到准确的数字全息再现像。结果表明，采用等效距离对数字全息图进行波前重建的结果与采用柯林斯公式重建的结果一致，此方法能够简化光波通过非单一介质时对数字全息图的波前准确重建。该研究结果可为显微数字全息及数字全息检测应用提供有益的参考。Abstract: In order to obtain accurate wavefront reconstruction field of digital holography, theoretical analysis and experiments of common wavefront reconstruction algorithms were made. Equivalent distance of light wave propagating through single medium was obtained. The related parameters commonly used in wavefront reconstruction formula were modified by using equivalent distance. The results of reconstruction of digital hologram with Collins formula and with equivalent distance were compared and analyzed. It was found that when light passing through non single medium, accurate digital holographic image could be obtained by reconstruction formula using Collins formula or equivalent distance correction. The results show that the results of wavefront reconstruction using equivalent distance of digital hologram are consistent with the results obtained by Collins formula reconstruction. This method can be used to simplify wavefront reconstruction of digital hologram when light wave passes through single medium. The results provide useful reference for microscopic digital holography and application of digital holography detection.
-
[1] PICART P, LEVAL J, MOUNIER D, et al. Some opportunities for vibration analysis with time averaging in digital Fresnel holography[J]. Applied Optics, 2005, 44(3):337-343. doi: 10.1364/AO.44.000337 [2] LI J Ch, CHEN Zh Y, ZHAO Sh, et al. Anti-calculation and its application of collins formula in wavefront reconstruction[J]. Chinese Journal of Lasers, 2005, 32(11): 1489-1494(in Chinese). [3] KEMPER B, GERT B B. Digital holographic microscopy for live cell applications and technical inspection[J]. Applied Optics, 2008, 47(4):A52-A61. doi: 10.1364/AO.47.000A52 [4] WANG H Y, ZHAO B Q, SONG X F. Focal depth of Fresnel digital holography imaging system[J]. Acta Optical Sinica, 2009, 29(2):374-377(in Chinese). doi: 10.3788/AOS [5] HU H F, WANG X L, ZHAI H Ch, et al. Time resolved optical diagnosis of intense femtosecond laser ablation of silica glass[J]. Acta Physica Sinica, 2011, 60(1):01709(in Chinese). [6] QIAN X F. Holography wavefront reconstruction adjustable magnification phase distortion[J]. Laser & Optoelectronics Progress, 2015, 52(5):48-57 (in Chinese). [7] ZHOU W J, HU W T, GUO L, et al. Experimental study of digital holographic tomography by a few projections[J]. Acta Physica Sinica, 2010, 59(12):8499-8511(in Chinese). [8] PASCAL P, LEVAL J. General theoretical formulation of image formation in digital Fresnel holography[J]. Journal of the Optical Society of America, 2008, A25(7):1744-1761. [9] GUI J B, SONG Q H, LI J Ch, et al.Realization and comparison of wave front reconstruction algorithms commonly used in colour digital holography[J]. Laser Techlonogy, 2015, 39(2): 176-181(in Chinese). [10] SONG X F, YU M J, WANG H Y, et al.Effect of reference intensity ratio to object on reconstructed image quality in digital holography[J]. Laser Techlonogy, 2014, 38(6): 859-862(in Chinese). [11] LI J Ch. Diffraction computing and digital holography[M].Beijing: Science Press, 2014:240-249(in Chinese). [12] POON T C. Digital holography and three-dimensional display: principles and applications[M]. New York, USA: Springer, 2006:110-118. [13] LI J Ch. Focal depth research of digital holographic reconstructed image[J]. Acta Physica Sinica, 2012, 61(13): 1342023(in Chinese). [14] COLLINS S A. Lens-systems diffraction integral written in terms of matrix optics[J]. Journal of the Optical Society of America, 1970, 60(9):1168-1177. doi: 10.1364/JOSA.60.001168 [15] LI J Ch, LI Ch G. Algorithm study of collins formula and inverse collins formula[J]. Applied Optics, 2008, 47(4):A97-A102. doi: 10.1364/AO.47.000A97 [16] LV B D. Laser optics-beam description, transformation and transmission optical cavity of technical physics[M]. 3rd ed. Beijing: Higher Education Press, 2003:33-43(in Chinese). [17] LI J Ch, LOU Y L, GUI J B, et al. Digital holographic detection of optical matrix elements in optical system[J]. Acta Optica Sinica, 2013, 33(2):0209001 (in Chinese). doi: 10.3788/AOS [18] JIANG H Zh, ZHAO J L, DI J L, et al. Numerically correcting the joint misplacement of the sub-holograms in spatial synthetic aperture digital Fresnel holography[J]. Optics Express, 2009, 19(21):18836-18842. -
点击查看大图
图(9)
计量
- 文章访问数: 8209
- HTML全文浏览量: 6332
- PDF下载量: 15
- 被引次数: 0
