Infrared background suppression algorithm based on guided filtering and fuzzy algorithm
-
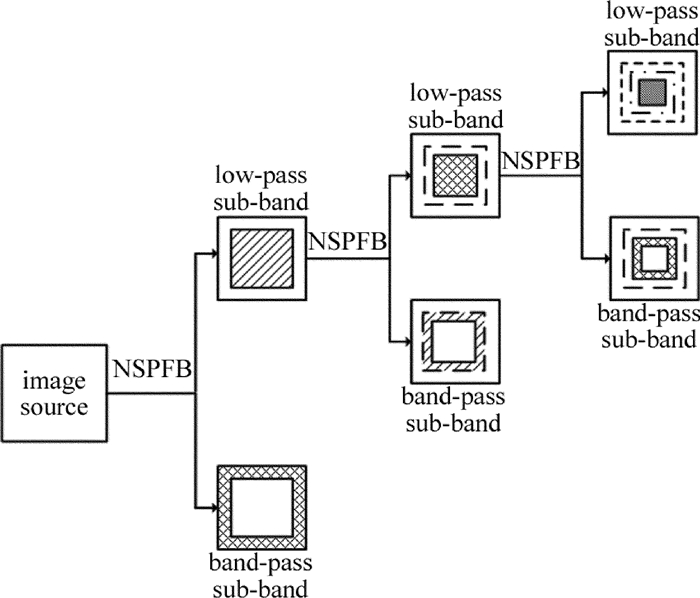
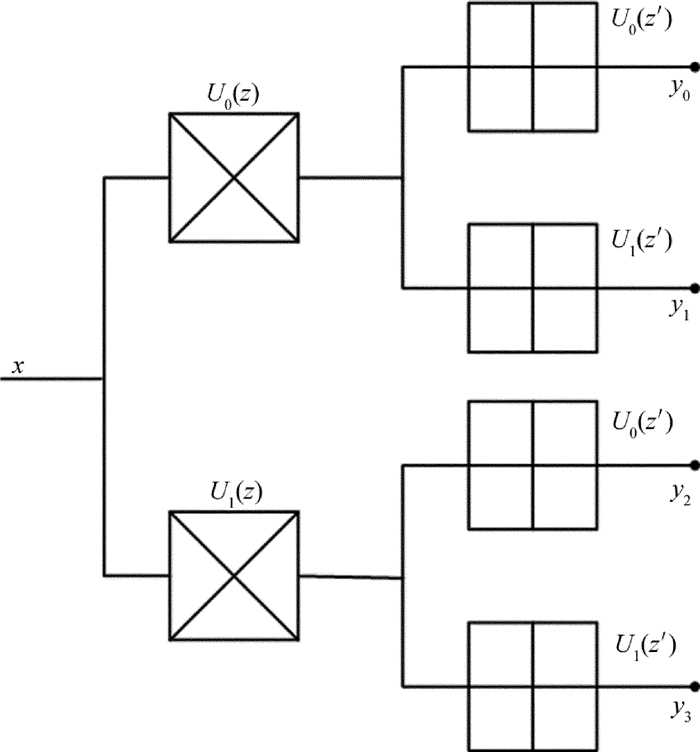
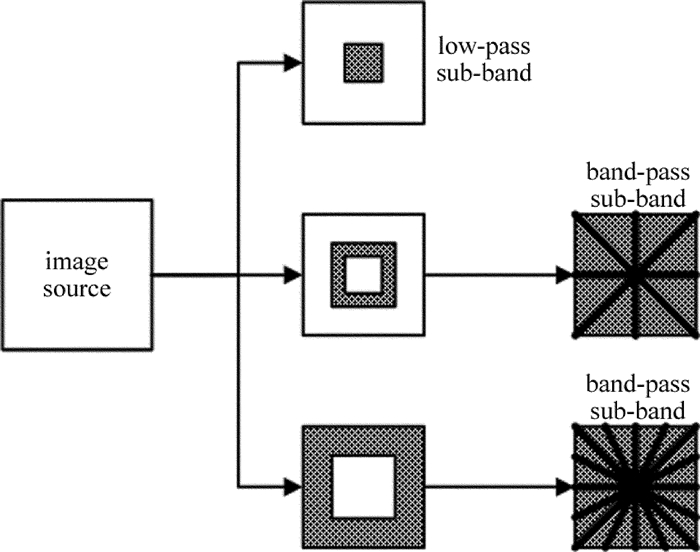
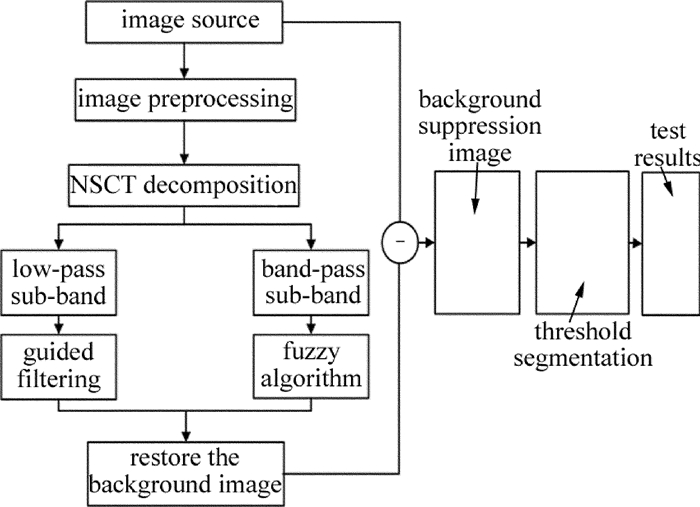
摘要: 为了减少背景对红外小目标检测结果的影响,同时降低检测虚警率,采用了基于引导滤波和模糊算法的红外背景抑制算法,利用非下采样轮廓波多尺度、多方向的分解机制,将红外序列图像分解为低通子带和带通子带;再利用引导滤波对低通子带处理,以平滑图像、抑制噪声、增强背景细节;带通子带则采用模糊算法处理,实现目标和残留背景分离;最后将各子带图像通过非下采样轮廓波逆变换,得到了背景抑制图像。结果表明,该方法可以将均方误差降至5~10,有效抑制了背景,突出了目标。该研究为提高复杂背景下的红外小目标检测精度提供了支持。Abstract: In order to reduce the influence of background on detection results of infrared small targets and reduce false alarm rate, infrared background suppression algorithm based on guidance filter and fuzzy algorithm was adopted. The infrared image was decomposed into low-pass band and band-pass band by using multi-scale and multi-direction decomposition mechanism of non sampled contour. The guided filter was used to process low-pass sub-band to smooth images, suppress noise and enhance background details. Band-pass sub-band was processed by fuzzy algorithm to seperate the target from the residual background. Background suppression image was obtained by changing subband images through non subsampled contour inversion. The results show that, the method can reduce mean square error to 5~10, and effectively suppress the background and highlight the target. This study provides the support for improving the detection accuracy of infrared small targets in complex background.
-
引言
光纤复合架空线路在电力系统中应用非常广泛,常见的有地线复合光缆,又叫光纤复合架空地线(optical fiber composite overhead ground wire, OPGW)[1-2]和光纤复合相线(optical phase conductor, OPPC)[3]。光纤复合架空线路在长期运行中会遭受一系列外界应力的作用,常见的有覆冰、外力、雷击、山火、舞动等[4-8],容易发生故障,非常有必要监测其状态以保障其安全运行。随着工农业的发展和人民生活水平的提高,对供电可靠性提出了更高的要求,因此对包括架空线路在内的输变电设备的智能化提出了更高的要求,要求其具有自我感知能力。
基于视频、图像的监测方法[9-10]可以有效反映线路运行状态,但大量图像给后续处理带来了较大的难度,同时针对较长线路其效率偏低。光纤传感技术在近年来取得了长足的进步[11-12]。基于架空线路复合的光纤,采用布里渊散射技术[13]能采集光纤沿线的应变、温度及振动信息[14-15]。该方式的突出优点是光纤复合线路自带的光纤即为传感器,同时能显著提升线路的自我感知能力。由于温度和应变与布里渊频移成线性关系[16],通常采用布里渊频移来测量应变和温度。常规的扫频法是通过测量一个完整的布里渊谱来获得布里渊频移,但为了保证信噪比(signal-to-noise ratio, SNR)每个频率点需要叠加数千次,且要涉及多达数十个频率点的测量,测量时间较长。为了提高测量的实时性,有人提出采用单斜坡法[17]测量光纤的温度和应变,该方法无需扫频,仅测量单点增益,即可计算布里渊频移,加快了测量速度。目前针对该方法的动态范围扩大和准确性提升以及应用方面[18-20]已开展了相关研究,取得了不错的效果。但就智能化光纤复合架空线路来说,单斜坡法的应用条件,包括工作点选择、信噪比和布里渊频移对测量结果准确性影响方面的系统研究尚鲜见报道。
为了解决该问题,本文作者基于实际测量得到的架空线路中复合光纤的布里渊谱,采用基于伪Voigt模型[21]的谱拟合法获得了较为准确的光纤沿线布里渊频移,实现了基于伪Voigt模型的单斜坡法用于布里渊频移计算;基于谱拟合法系统研究了工作点增益的信噪比及布里渊频移对单斜坡法误差的影响规律,给出了满足准确性要求的信噪比范围及不同布里渊频移下的临界信噪比,并给出了工作点选择的建议。
1. 智能化架空线路应变感知方法
以典型的OPGW为例[2],其结构如图 1所示。图 1中光单元中的部分光纤可用于传感。传感光纤中的脉冲光在传输过程中会发生布里渊散射,在入射端通过光电二极管等方式测量背向布里渊散射光功率,获得光功率与频移,即背向散射光频率与入射光频率之差的关系可得布里渊谱。背向散射光功率最大值对应的频移为布里渊频移,根据布里渊频移即可计算光纤的温度或应变。架空线路在运行中可能遭受的故障多会使线路温度、应变发生变化,比如覆冰会导致线路承受应变,覆冰段与不覆冰段随环境温度变化时线路温度变化规律不同;舞动对应应变的周期性变化;外力破坏导致线路承受应变发生变化;山火会使线路温度升高,由于热膨胀也会使线路承受应变。
2. 基于单斜坡法的布里渊频移提取
2.1 谱拟合法
考虑到实测布里渊谱满足的分布,故采用基于如下式所示的伪Voigt模型的最小二乘拟合法逼近布里渊谱,根据拟合结果来获得布里渊频移:
gB(ν)=g1(ΔνB/2)2(ν−νB)2+(ΔνB/2)2+g2exp[−(4ln2)(ν−νB)2(ΔνB)2] (1) 式中,νB为布里渊频移;ν为频率;gB为布里渊增益;ΔνB为线宽;g1和g2分别为洛伦兹和高斯模型布里渊增益峰值。目标函数如下式所示:
E=N∑n=1[gв (νn)−gв, n ]2 (2) 式中,νn和gB, n分别为第n个扫频点和对应的布里渊增益测量值,E为增益误差的平方和,N为扫频点数。
光纤温度和应变与布里渊频移近似成线性关系,如果考虑到同一时刻架空线路上温度近似为一固定值,则应变可直接由布里渊频移计算,如下式所示:
ε=(νB−νB,0)/Cν,ε (3) 式中, νB, 0为温度固定且无应变下的布里渊频移;Cν, ε为布里渊频移的应变系数,典型值为20 με/MHz;ε为应变。由以上分析可知,根据布里渊频移误差可直接获得应变误差,后续的研究多侧重于布里渊频移误差。考虑到Levenberg-Marquardt算法适合于求解以上的非线性最小二乘问题,选择它来优化(2)式。
2.2 单斜坡法
与谱拟合法不同,单斜坡法仅需要获得工作点对应的布里渊增益,无需耗时的扫频过程。设ν0为工作点频率,取光纤沿线布里渊谱的真实参数,即光纤上布里渊频移和线宽的平均值分别为10.83 GHz和149.57 MHz,g1=3.91×10-4,g2=1.67×10-3,ν0分别选择为10.755 GHz和10.905 GHz,且分别位于布里渊频移的左侧和右侧,布里渊频移与工作点增益满足如图 2所示的关系。需要注意的是,实际使用时工作点可以取在布里渊频移的左侧,也可以取在布里渊频移的右侧。这样根据实测的工作点布里渊增益及以上关系即可获得布里渊频移。
3. 单斜坡法的验证
采用布里渊光时域反射计(Brillouin optical time-domain reflectometry, BOTDR)实测了约22 km OPGW复合光纤上的布里渊谱,测量参数如下:扫频范围为10.7 GHz~10.95 GHz;入射脉冲光宽度为10 ns;扫频间隔为1 MHz;叠加平均次数为214;采样分辨率为0.5 m。采用基于Voigt模型的谱拟合法获得布里渊频移,计算得到布里渊频移如图 3a所示。考虑到谱拟合法在扫频点数足够多时布里渊频移准确性能达到较大值,而且此时也难以有其它方法进一步显著提高其准确性。因此,以基于Voigt模型的谱拟合法算得谱参数为准确值。光纤沿线布里渊频移和线宽的均值分别为10.83 GHz和149.57 MHz,暂时设定工作点为光纤沿线布里渊频移均值减去一半的线宽,即工作点频率为10.755 GHz。得到单斜坡法的计算结果也一并画于图 3a中;两种方法计算结果之差如图 3b所示;为了更加清晰展示结果,光纤头部和尾部处两种方法的计算结果分别如图 3c和图 3d所示。由图 3a和图 3b可知,在光纤头部两种方法算得布里渊频移比较接近,随着光纤位置逐渐靠近尾端,二者差距逐渐增大,甚至最大误差可达76.03 MHz,对应的应变误差为1520.52 με。以上情况在图 3c和图 3d中得到了清晰的展示。根据以上研究结果可知,单斜坡法在光纤复合架空线路沿线应变测量方面具有可行性,在某些情况下单斜坡法可能会产生较大的误差,不是所有情况下光纤复合线路光纤沿线应变的测量都可以采用该方法。因此,后续需要研究该方法的适应性。
![图 3 单斜坡法与谱拟合法计算结果的比较]() 图 3 单斜坡法与谱拟合法计算结果的比较a—两种方法的计算结果b—两种方法的计算结果之差c—两种方法的计算结果(光纤头部) d—两种方法的计算结果(光纤尾部)Figure 3. Comparison of calculation results between slope-assisted technique and spectrum fitting methoda—calculation results by two methods b—difference in calculation results by two methods c—calculation results by two methods of head of optical fiber d—calculation results by two methods of tail of optical fiber
图 3 单斜坡法与谱拟合法计算结果的比较a—两种方法的计算结果b—两种方法的计算结果之差c—两种方法的计算结果(光纤头部) d—两种方法的计算结果(光纤尾部)Figure 3. Comparison of calculation results between slope-assisted technique and spectrum fitting methoda—calculation results by two methods b—difference in calculation results by two methods c—calculation results by two methods of head of optical fiber d—calculation results by two methods of tail of optical fiber4. 信噪比和布里渊频移的影响
根据第3节中单斜坡法原理可知,工作点与布里渊频移差距及工作点增益的信噪比会影响单斜坡法的准确性,本节中对该问题开展研究。实测布里渊谱模型及噪声服从的模型与仿真采用的模型必然存在差距, 所以采用实测谱数据的研究结果具有更高的可靠性。但由于实测布里渊谱对应参数的精确值未知,如何可靠确定信噪比等参数非常关键。伪Voigt模型在不同入射光脉宽下均可以有效逼近实测布里渊谱,准确性高于洛伦兹模型和高斯模型。因此,本文中通过基于伪Voigt模型的谱拟合法可以获得比较准确的布里渊频移和布里渊谱参数。基于这些数据得到不同工作点与布里渊频移之差下, 信噪比对布里渊频移误差的影响如图 4所示。不同信噪比下工作点与布里渊频移之差对布里渊频移误差的影响如图 5所示。
由图 4可知,随着工作点增益信噪比的增加,单斜坡法算得布里渊频移误差逐渐下降。根据二者的关系,采用如下式所示的指数规律进行拟合,拟合结果一并画于图 4中。
Eν=aexp(bR) (4) 式中,Eν为布里渊频移误差(MHz);a和b为待优化变量;R为信噪比(dB)。
显然,单斜坡法算得布里渊频移误差随工作点增益信噪比增加近似成指数规律下降。由图 5可知,不同信噪比下,随着布里渊频移与工作点频率之差的增加,布里渊频移误差先快速下降,达到谷值后略有增加。基本上当0.55 < (νB-ν0)/ΔνB < 0.95时, 布里渊频移误差取到最小值。为了更加准确获得最佳工作点,根据以上所有数据进行整理获得了工作点与布里渊频移之差与单斜坡法平均误差的关系, 如图 6所示。
图 6中工作点频率对误差的影响与图 5类似。由图 6可知,工作点要满足(5)式,这样单斜坡法算得布里渊频移误差接近最小值。
(νB−ν0)/ΔνB=0.5 (5) 由于光纤沿线的布里渊频移会变化,而工作点频率应该是一个固定值,因此工作点应该满足下式:
ν0=¯νB−ΔνB/2 (6) 式中,¯νB为光纤上布里渊频移的平均值。需要注意的是,(6)式中工作点频率始终小于布里渊频移,如果将式中的“-”改为“+”,则工作点频率始终大于布里渊频移。
综上所述,图 3c中两种算法计算结果差距较小,是因为光纤头部测得布里渊谱信噪比较高,此时两种算法的准确性均较高,因此二者算得布里渊频移比较接近。图 3d中两种算法计算结果差距较大,是因为随着光纤位置逐渐靠近尾端,测得布里渊谱信噪比逐渐下降,两种算法的误差均逐渐增大,尤其是单斜坡法,故二者差距逐渐增大。
5. 方法适应性研究
本节中研究单斜坡法对信噪比和工作点选择的要求,仍然采用第4节中的实测数据。工作点与布里渊频移之差以及工作点处增益信噪比下的单斜坡法误差如图 7a所示。由于低信噪比下单斜坡法误差很大,对方法适应性的研究产生了干扰,为了更加清楚地展示结果,也给出了信噪比大于10 dB、20 dB和25 dB下的误差,分别如图 7b、图 7c和图 7d所示。
由图 7可知,工作点处增益的信噪比和工作点频率(布里渊频移)对单斜坡法误差有显著影响,尤其是信噪比影响更大,随着信噪比增加,误差显著减小。由图 7b~图 7d可知,随着工作点越靠近布里渊频移,误差越大。由图 2可知,这是因为随着工作点越靠近布里渊频移,dνB/dgB(ν0)越大,即同样程度的噪声给νB测量带来的误差就越大。而当νB-ν0 < 0时,本文中默认为νB-ν0>0,也会产生误差。信噪比为10 dB, 20 dB和25 dB时,单斜坡法算得布里渊频移的最大误差分别为20.85 MHz,4.90 MHz和2.59 MHz,对应的应变误差分别为417.07 με,98.09 με和51.86 με。考虑到单斜坡法的定位是一种快速的测量方法,对准确性没有过高要求,基本上可以认为信噪比不小于25 dB时单斜坡法的准确性能满足一般的要求,当然,这时候也要求νB-ν0>0。考虑到一定准确性要求下,不同布里渊频移(布里渊频移与工作点频率差距)时对增益信噪比的要求不同,本文中通过计算也给出了3 MHz(60 με)误差、不同布里渊频移时的临界信噪比,如图 8所示。根据架空线路沿线布里渊频移的大致分布以及该图, 即可获得满足准确性要求时对工作点处增益信噪比的要求。
下面采用第4节中的单斜坡法算得光纤沿线布里渊频移误差验证前面的分析。给出了光纤沿线布里渊频移与工作点差距(见图 9a)。图 9b中给出了工作点增益的信噪比(工作点由(6)式确定)以及误差为3 MHz时对应的信噪比。显然,随着光纤位置逐渐靠近尾端,信噪比小于临界值的布里渊谱的概率逐渐增大。图 9c中给出了工作点增益信噪比小于临界值的概率(比例)。显然,此概率随光纤位置逐渐靠近尾端而逐渐增大,与图 3b中单斜坡法误差变化规律在定性上能很好吻合。
为了进一步验证以上分析,采用BOTDR实测了某OPGW复合光纤的布里渊谱,测量参数如下:扫频范围为10.4 GHz~11.2 GHz;入射脉冲光宽度为20 ns;扫频间隔为5 MHz;叠加平均次数为8192;采样分辨率为0.5 m。基于单斜坡法和谱拟合法计算得到光纤上布里渊频移如图 10a所示:两种方法的差距以及单斜坡法误差大于3 MHz的概率如图 10b所示。针对同样的布里渊谱,谱拟合法算得光纤上布里渊频移与工作点之差画于图 11a中;工作点处增益的信噪比以及3 MHz误差对应的临界信噪比如图 11b所示;布里渊增益信噪比小于临界值的概率与光纤位置的关系如图 11c所示。显然图 11c中曲线与图 10b中单斜坡法误差大于3 MHz的概率与光纤位置的关系能很好吻合,也基本验证了本节中分析的可靠性。由于布里渊谱测量时间与扫频点数成正比,而本案例下布里渊谱扫频点数为161,单斜坡法仅需要测量单点增益,故单斜坡法的谱测量时间仅为谱拟合法谱测量时间的1/161。两种方法计算一次布里渊频移耗时分别为86.26 μs和53.81 ms,因此前者耗时仅为后者的1/600左右。
6. 结论
针对大量实测布里渊谱对单斜坡法在光纤复合架空线路中光纤沿线应变测量及其适应性开展了较为系统的研究。
(1) 单斜坡法在基于布里渊散射的光纤复合架空线路沿线应变测量方面具有可行性,可使光纤沿线应变的测量时间和计算时间减少到谱拟合法的1/161和1/600左右。
(2) 随着工作点增益信噪比增加,布里渊频移误差近似成指数规律下降;随着布里渊频移与工作点频率之差的增加,布里渊频移误差先快速下降,达到谷值后略有增加,最佳工作点建议选择为(νB-ν0)/ΔνB=0.5。
(3) 工作点增益的信噪比不小于25 dB且工作点频率始终小于(或大于)布里渊频移时,该方法准确性基本能满足要求;进一步地,也可以根据得到的临界信噪比曲线粗略分析单斜坡法可能产生的误差。
-
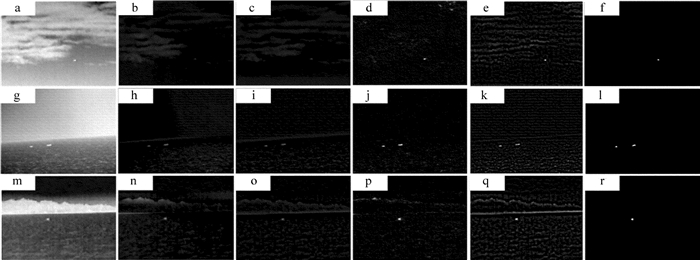
Table 1 Comparison among the experimental results
Fig. 5m Fig. 5g Fig. 5a MSE PSNR MSE PSNR MSE PSNR top-hat 16.6446 32.8435 13.0185 36.7370 12.3329 36.1820 GIF 15.5397 33.1418 13.0016 36.7426 12.0448 36.2847 RPCA 10.5324 34.8309 6.6929 36.8000 6.2712 37.0826 NSCT 25.6984 30.9572 10.8570 37.1255 5.8153 39.4470 algorithm of this paper 9.9399 35.0824 5.8548 37.3811 5.1063 40.0116 -
[1] RONG Sh H, LIU G, ZHOU H X, et al. Infrared dim and small target background suppression based on the improved shearlet transformand the guide filter[J]. Acta Photonica Sinica, 2015, 44(2):210002(in Chinese). DOI: 10.3788/gzxb
[2] YAN G Sh, BI W Zh. Detection algorithm of small target based on regional singularity filter[J]. Optical Technique, 2007, 33(2):163-152(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-GXJS200702000.htm
[3] QIN H L, ZHOU H X, LIU Sh Q, et al. Total variation for dim and small target background suppression[J]. Optical Technique, 2009, 35(4):596-598(in Chinese).
[4] QIN H L, YAO K K, ZHOU H X, et al. Nonsubsampled directional filter banks for infrared complex ground background suppression[J]. Semiconductor Optoelectronics, 2011, 32(4):560-563(in Ch-inese). http://d.old.wanfangdata.com.cn/Periodical/bdtgd201104030
[5] LI J, MA J N, LI Sh J, et al. Background suppression for infrared dim small target detection based on spatial-temporal filter[J]. Semiconductor Optoelectronics, 2017, 38(3):396-400(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/bdtgd201703019
[6] GE W, JI P Ch, ZHAO T Ch. Infrared and visible light images fusion of fuzzy logic on NSST domain[J]. Laser Technology, 2016, 40(6):892-896(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs201606024
[7] WU Y Q, LUO Z J, WU W Y. A method of small target detection in infrared image based on non-subsampled contourlet transform[J]. Journal of Image & Graphics, 2009, 14(3):477-481(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-ZGTB200903018.htm
[8] WU T A, HUANG Sh C, YUAN Zh W, et al. NSCT combined with SVD for infrared dim target complex background suppression[J]. Infrared Technology, 2016, 38(9):758-764(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hwjs201609008
[9] FENG Y. Detection of dim and small infrared targets based on the improved singular value decomposition[J]. Laser Technology, 2016, 40(3):335-338(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs201603007
[10] da CUNHA A L, ZHOU J, DO M N. The non-subsampled contourlet transform:theory, design and applications[J]. IEEE Transactions on Image Proecessing, 2006, 15(10):3089-3101. DOI: 10.1109/TIP.2006.877507
[11] PENG Zh, ZHAO B J. Novel scheme for infrared image enhancement based on contourlet transform and fuzzy theory[J]. Laser & Infrared, 2011, 41(6):635-640(in Chinese). http://ieeexplore.ieee.org/document/6023751/
[12] HE K, SUN J, TANG X OU. Guided image filtering[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 35(6):1397-1409. http://d.old.wanfangdata.com.cn/Periodical/zgtxtxxb-a201207002
[13] LI X H, DONG A G, FENG J H. Regional fusion algorithm of i-mages based on multistage guide filters[J]. Laser Technology, 2016, 40(5):756-761(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-JGJS201605029.htm
[14] KANG Ch Q, CAO W P, HUA L, et al. Infrared image denoising algorithm via two-stage 3-D filtering[J]. Laser & Infrared, 2013, 43(3):261-264(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgyhw201303008
[15] ZHANG W. An improved method of image fuzzy enhancement[J]. Life Science Instruments, 2006, 4(3):29-31(in Chinese).
[16] LUO Y, YANG H M. An improved fuzzy enhancement algorithm of robot digital landmark based on Otsu adaptive threshold[J]. Optics & Optoelectronic Technology, 2010, 8(1):35-38(in Chinese).
-
期刊类型引用(7)
1. 刘宣呈,陈根余,操坤,曹明月,梅枫. 成形砂轮激光修整的多轮廓图像合成检测方法. 激光技术. 2024(03): 395-404 .  本站查看
本站查看
2. 何易德,朱斌,姜湖海,刘书信,李黎明,胡绍云. 红外图像多尺度统计和应用先验去模糊模型. 激光技术. 2023(03): 360-365 .  本站查看
本站查看
3. 何易德,朱斌,司晨,毛锐. 基于红外视景仿真技术的导向滤波算法. 激光技术. 2021(02): 233-239 .  本站查看
本站查看
4. 朱金辉,张宝华,谷宇,李建军,张明. 基于双邻域对比度的红外小目标检测算法. 激光技术. 2021(06): 794-798 .  本站查看
本站查看
5. 王宁,周铭,杜庆磊,王冰. 一种红外图像快速目标检测方法. 弹箭与制导学报. 2020(04): 24-28+33 .  百度学术
百度学术
6. 刘晓玲,牛海春,宋海燕,秦富贞. 复杂环境下弱信号中的红外小目标自动检测. 激光杂志. 2020(10): 82-86 .  百度学术
百度学术
7. 王宁,周铭,杜庆磊,王冰. 基于Otsu准则的红外图像快速分割算法. 空军预警学院学报. 2019(02): 88-92 .  百度学术
百度学术
其他类型引用(4)




 下载:
下载: