Deblurring model of infrared image multi-scale statistics and application of prior
-
摘要: 为了提高特定应用场景的红外导引头成像质量，采用了统计导引头图像对成像环境和应用场景建模的方法, 一方面用L1/L2范数对复原图像进行约束，保持多尺度成像细节信息；另一方面用稀疏的拉普拉斯分布对迭代模糊核进行约束，保持对红外成像内容的约束, 并采用计算图像细节信息进行了自适应变化核。结果表明，建立的图像复原约束模型能有效地提升成像质量，凸显图像边缘, 其对比度增强系数指标提高了20%~50%，峰值信噪比提高了0.8~3.4，图像像素的模糊检测累积概率提高了0.3~0.5。该研究对复杂场景和动载体成像处理有一定的帮助。Abstract: In order to improve specific application imaging quality of infrared seeker, a model for imaging condition and application scene was constructed by using statistical image of infrared image seeker. On the one hand, L1/L2 norm was used to constrain the restored image according to the characteristics of multi-scale imaging, which kept details in the iterative restoration. On the other hand, a sparse Laplacian distribution was used to constrain fuzzy kernel, and to maintain image's content. Image kernel size can be adjusted adaptively by calculating the image details. The result shows that the prior constrain algorithm of this paper can effectively improve the image quality. In addition, the evaluation index is improved by this prior design, the contrast enhancement coefficient index is increased by 20%~50%, the peak signal to noise ratio is increased by 0.8~3.4, and the cumulative probability of blur detection is increased by 0.3~0.5.This study is helpful for complex scene and moving vector imaging.
-
引言
图像去模糊以观测图像计算复原真实图像，属于计算图像范畴，是探测成像的逆过程[1]。图像去模糊研究是计算机视觉中活跃的研究领域之一[2-5]，包括探测成像系统原理、视觉投影几何成像模型和光线传输链路等，分层次建模，复原真实图像[6-10]；计算图像研究通过建立先验约束模型和超参数估计，采用盲反卷积模型优化求解复原真实图像[11-14]。图像计算研究基于贝叶斯最大后验模型或期望变分模型[15-16]，依次建立数据拟合项、先验约束项，并优化求解模型，复原图像。
红外成像具有全天候、抗干扰等优点，在精确制导领域应用广泛。红外研究包括全变分(total variation, TV)先验设计[17]、导向滤波设计[18]等。此类图像处理算法在红外导引头精确制导领域有广泛应用，但缺乏其它红外精确制导的应用。
多尺度是挖掘图像信息的重要方式，图像通过多尺度几何刻画表示，获取其深层信息，即多尺度成像序列是体现成像环境深层信息的重要样本。红外导引头不断逼近目标属于典型的多尺度成像过程，因此红外图像去模糊算法研究具有一定的实际应用价值。红外导引头成像特征以复杂地物、干扰为主, 其统计信息与可见光图像信息差距较大，且成像载体受外界扰动[8-9]。因此，对场景图像的特性进行对比分析，统计导引头红外成像独特性质，建立先验约束，对复原红外导引头图像具有实际意义。
1. 相关分析
1.1 典型目标红外特性分析
物体发射率和表面温度是影响自身红外辐射的主要物理参数，双向反射分布函数则反映物体反射外界辐射参数。地表的辐射平均温度为290 K，相应的峰值波长约为10 μm，与其中一个大气窗口中间值接近；发动机、动力设施等热源与另一个大气窗口中间值4 μm，720 K的温度相对应。因此，长波红外更适于探测平均温度较低、建筑物靶标桥梁等静态自然目标；中波红外更适于温度较高的人为金属运动目标。
1.2 大气效应探测成像分析
大气本身对目标/场景辐射有吸收和散射作用，造成有效辐射量的衰减。大气对辐射强度的衰减作用称之为消光，大气消光作用主要是由大气中各种气体成分及气溶胶粒子对辐射的吸收与散射造成的，在辐射的传输过程中，目标/场景辐射量与气体分子和气溶胶粒子相互作用。大气不同成分与不同物理过程造成的消光效应具有线性叠加特性。大气辐射和大气反射辐射都会使目标/场景对比度下降，影响探测成像系统；同时其自身热辐射在不确定性的混叠于目标/场景辐射从而降低成像对比度，使景物信息衰减，图像边缘模糊。
2. 多尺度信息与应用场景的先验模型
2.1 多尺度红外图像统计特性分析与先验模型
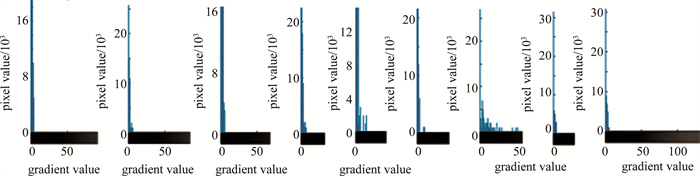
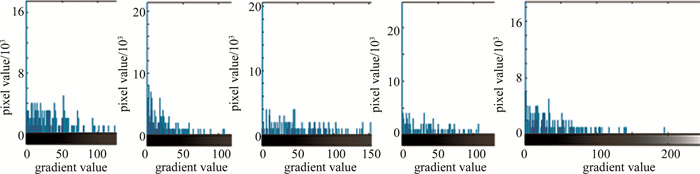
本文作者以长波红外导引头图像作为研究对象，获取大量实时导引头图像序列和部分仿真生成图像数据，见图 1。通过统计上述类似的导引头红外图像的梯度信息，得到图 2和图 3。
![图 2 清晰度较高的红外图像梯度统计信息]()
图 2 清晰度较高的红外图像梯度统计信息Figure 2. High-resolution infrared image gradient statistics result![图 3 清晰度不高的红外图像梯度统计信息]()
图 3 清晰度不高的红外图像梯度统计信息Figure 3. Low-resolution infrared image gradient statistics result图 2和图 3的纵轴表示图像数据点的多少(单位为103个像素点)，横轴表示图像中梯度值的分布(0~255)。从图 2和图 3中可以看出，图像越清晰，图像相邻点的梯度越集中于0附近，图像越模糊，图像相邻点梯度分布越广；图像纹理越丰富，梯度统计信息越明显；图像越模糊，梯度信息越分散，且0附近的统计信息较少。图像中的目标朝向也会引起水平或垂直梯度的统计不同。图像是水平目标，则水平梯度较明显，垂直梯度较弱; 反之则水平梯度影响较小，垂直梯度影响较大。
2.2 导引头应用场景的红外图像特性分析与先验模型
图像导引头应用场景主要包括海面(港口)、郊区、沙漠、草地、雪地等，目标多为典型车辆、飞机、舰船、建筑物、靶标等。从图 1可知，导引头应用图像比常规图像的纹理较少，梯度统计信息少，但较模糊图像的梯度信息也满足分散特性，较清晰图像的梯度信息更加集中，更适合超稀疏先验约束模型。图像边缘和梯度凸显图像信息，在模型设计和实验对比中具有重要作用。
2.3 本文中先验约束模型的设计
通过上述分析，综合考虑导引头红外应用场景特征和不断逼近目标的多尺度成像特征，由于不同尺度下图像细节丰富度变化较大，因此对图像先验约束采用L1/L2范数模型，即引用设计为：
\begin{array}{c} Q(\boldsymbol{u})=Q\left(\boldsymbol{D}_x \boldsymbol{u}, \boldsymbol{D}_y \boldsymbol{u}\right)= \\ \sum\limits_{(i, j)} \frac{\left\|\left[\boldsymbol{D}_x \boldsymbol{u}\right]_i^2+\left[\boldsymbol{D}_y \boldsymbol{u}\right]_j^2\right\|_1}{\left\|\left[\boldsymbol{D}_x \boldsymbol{u}\right]_i^2+\left[\boldsymbol{D}_y \boldsymbol{u}\right]_j^2\right\|_2} \end{array} (1) 式中，Dx和Dy为梯度算子，x, y表示图像的行和列，u为需复原图像(i, j)的图像邻域，Q(u)表示关于u的能量先验泛函。
L2范数是对图像梯度信息的总和，在分母中体现归一化的作用，即多尺度条件下细节信息的统一。L1范数是对图像先验约束的稀疏性表示，导引头成像场景物和目标与工业界可见光图像相比较少，其边缘和梯度信息具有更稀疏的特性，因此需采用梯度约束。
由于导引头成像信息、场景物以及目标所呈现的细节和梯度信息不够丰富，同时不同尺度下模糊核变化，因此对模糊核先验约束采用变化适应的拉普拉斯分布[1]。
假设盲反卷积去模糊模型的噪声为高斯噪声，上述两约束作为图像和图像核的先验约束，则盲反卷积去模糊模型可表示为：
\begin{array}{c} L(\mathit{\boldsymbol{u}}, \mathit{\boldsymbol{h}}) = \frac{\gamma }{2}\left\| {\mathit{\boldsymbol{u}} \times \mathit{\boldsymbol{h}} - \mathit{\boldsymbol{g}}} \right\|_2^2 + Q(\mathit{\boldsymbol{u}}) + R(\mathit{\boldsymbol{h}}) = \\ \frac{\gamma }{2}\left\| {\mathit{\boldsymbol{u}} \times \mathit{\boldsymbol{h}} - \mathit{\boldsymbol{g}}} \right\|_2^2 + \frac{1}{\alpha }\sum\limits_{(i, j)} \mathit{\Psi } \left( {{\mathit{\boldsymbol{h}}_{i, j}}} \right) + \\ \sum\limits_{(i, j)} {\frac{{{{\left\| {\left[ {{\mathit{\boldsymbol{D}}_x}\mathit{\boldsymbol{u}}} \right]_i^2 + \left[ {{\mathit{\boldsymbol{D}}_y}\mathit{\boldsymbol{u}}} \right]_j^2} \right\|}_1}}}{{{{\left\| {\left[ {{\mathit{\boldsymbol{D}}_x}\mathit{\boldsymbol{u}}} \right]_i^2 + \left[ {{\mathit{\boldsymbol{D}}_y}\mathit{\boldsymbol{u}}} \right]_j^2} \right\|}_2}}}} \end{array} (2) 式中，L(u，h)表示u和h的图像反卷积去模糊模型泛函，h表示图像模糊核矩阵，γ为高斯分布精度，g表示输入观测图像，α为拉普拉斯分布参量, R(h)是关于h的泛函，Ψ(h)也是关于h的泛函。这里对R(h)进行分段处理：如果变量h < 0，则R(h)取0，反之则取Ψ(h)。(2)式的第1项是高斯噪声假设下数据拟合项，第2项为对清晰图像的先验约束设计，第3项为对成像模糊核的先验约束设计。
2.4 模型优化求解
盲反卷积去模糊模型采用交替迭代优化求解，由于图像噪声对结果影响较大，在迭代优化求解之前，采用双边滤波方法对图像进行去噪处理，详细算法求解流程见图 4。
在图 4中的step 2，为了初始化图像模糊核大小，采用[Dxu]i2+[Dyu]j2方法对多尺度图像细节信息进行统计分析。导引头图像与成像姿态、距离密切相关：在快速逼近目标过程中，末制导初期成像视角低平，俯仰角在零度附近，场景中物体较多，但由于距离较远，成像细节并不丰富，图像边缘信息较少；随着成像距离和角度的不断变化，俯仰角逐渐变小(为负数)，成像细节逐渐丰富，边缘信息逐渐增多；最后当成像为下视时，俯仰角几乎接近-90°，图像仅包含目标及其附近场景，此刻图像目标细节丰富，但是场景物远低于末制导初期，此刻的图像边缘信息最少。因此，导引头整个末制导阶段图像信息的变化过程呈现逐渐增多，到最后导引头姿态与目标正视时，细节信息最少。以末制导开始阶段的图像统计信息为基础，此时选择核矩阵大小为10 pixel×10 pixel，随着细节统计信息的翻倍，核矩阵依次变化为20 pixel×20 pixel、40 pixel×40 pixel，当统计信息急速降低到末制导开始阶段的一半时，核矩阵大小选择为80 pixel×80 pixel，并保持到最后时刻。
对于图 4中的step 3.1, 求解迭代复原图像，本文中采用增广拉格朗日算法(augmented Lagrange method, ALM)交替迭代优化求解目标泛函。将目标泛函拆分为只含其中一个变量的泛函，固定模糊核矩阵h，只考虑复原图像变量，即：
\begin{array}{c} f(\boldsymbol{u})=\frac{\gamma}{2}\|\boldsymbol{H} \boldsymbol{u}-\boldsymbol{g}\|_2^2+ \\ \sum\limits_{(i, j)} \frac{\left\|\left[\boldsymbol{D}_x \boldsymbol{u}\right]_i^2+\left[\boldsymbol{D}_y \boldsymbol{u}\right]_j^2\right\|_1}{\left\|\left[\boldsymbol{D}_x \boldsymbol{u}\right]_i^2+\left[\boldsymbol{D}_y \boldsymbol{u}\right]_j^2\right\|_2^2} \end{array} (3) 式中，H是模糊核矩阵h的傅里叶变换表示。设vx=Dxu, vy=Dyu，上述泛函表示为：
\begin{array}{c} f(\boldsymbol{u})= \\ \frac{\gamma}{2}\|\boldsymbol{H} \boldsymbol{u}-\boldsymbol{g}\|_2^2+\sum\limits_{(i, j)} \frac{\left\|\left[\boldsymbol{v}_x\right]_i^2+\left[\boldsymbol{v}_y\right]_j^2\right\|_1}{\left\|\left[\boldsymbol{v}_x\right]_i^2+\left[\boldsymbol{v}_y\right]_j^2\right\|_2} \end{array} (4) 式中，vx和vy为拉格朗日乘子。利用ALM将上述泛函表示为：
\begin{array}{c} f(\boldsymbol{u})=\frac{\gamma}{2}\|\boldsymbol{H} \boldsymbol{u}-\boldsymbol{g}\|_2^2+\sum\limits_{(i, j)} \frac{\left\|\left[\boldsymbol{v}_x\right]_i^2+\left[\boldsymbol{v}_y\right]_j^2\right\|_1}{\left\|\left[\boldsymbol{v}_x\right]_i^2+\left[\boldsymbol{v}_y\right]_j^2\right\|_2}+ \\ \frac{\alpha}{2}\left\|\boldsymbol{D}_x \boldsymbol{u}-\boldsymbol{v}_x-\boldsymbol{a}_x\right\|^2+\frac{\alpha}{2}\left\|\boldsymbol{D}_y \boldsymbol{u}-\boldsymbol{v}_y-\boldsymbol{a}_y\right\|^2 \end{array} (5) 式中，f(u)表示与u相关的泛函; ax与vx的意义一样，是ALM将约束条件写到目标泛函中而引入的变量。为了利于优化求解，将泛函中的变量u和v进行拆分，得到：
\begin{array}{c} f(\boldsymbol{u})=\frac{\gamma}{2}\|\boldsymbol{H} \boldsymbol{u}-\boldsymbol{g}\|_2^2+\frac{\alpha}{2}\left\|\boldsymbol{D}_x \boldsymbol{u}-\boldsymbol{v}_x-\boldsymbol{a}_x\right\|^2+ \\ \frac{\alpha}{2}\left\|\boldsymbol{D}_y \boldsymbol{u}-\boldsymbol{v}_y-\boldsymbol{a}_y\right\|^2 \end{array} (6) \begin{array}{c} f\left(\boldsymbol{v}_x, \boldsymbol{v}_y\right)=\sum\limits_{(i, j)} \frac{\left\|\left[\boldsymbol{v}_x\right]_2^2+\left[\boldsymbol{v}_y\right]_2^2\right\|_1}{\left\|\left[\boldsymbol{v}_x\right]_2^2+\left[\boldsymbol{v}_y\right]_2^2\right\|_2}+ \\ \frac{\alpha}{2}\left\|\boldsymbol{D}_x \boldsymbol{u}-\boldsymbol{v}_x-\boldsymbol{a}_x\right\|^2+\frac{\alpha}{2}\left\|\boldsymbol{D}_y \boldsymbol{u}-\boldsymbol{v}_y-\boldsymbol{a}_y\right\|^2 \end{array} (7) 设ax(k+1)=ax(k)－Dxu(k+1)+vx(k+1)，ay(k+1)=ay(k)－Dyu(k+1)+vy(k+1)，k=k+1，取初值ax(0)=0, ay(0)=0, k=0，对于上述泛函，执行：
\begin{array}{l} \operatorname{solve}\left[\boldsymbol{H}^{\mathrm{T}} \boldsymbol{H}+\frac{\alpha}{\gamma}\left(\boldsymbol{D}_x^{\mathrm{T}} \boldsymbol{D}_x+\boldsymbol{D}_y^{\mathrm{T}} \boldsymbol{D}_y\right)\right] \boldsymbol{u}^{(k+1)}=\boldsymbol{H}^{\mathrm{T}} \boldsymbol{g}+ \\ \ \ \frac{\alpha}{\gamma}\left[\boldsymbol{D}_x^{\mathrm{T}}\left(\boldsymbol{v}_x{ }^{(k)}+\boldsymbol{a}_x{ }^{(k)}\right)+\boldsymbol{D}_y^{\mathrm{T}}\left(\boldsymbol{v}_y{ }^{(k)}+\boldsymbol{a}_y{ }^{(k)}\right)\right] \end{array} (8) \begin{array}{c} \operatorname{LUT}\left(\left[\boldsymbol{D}_x \boldsymbol{u}^{(k+1)}-\boldsymbol{a}_x{ }^{(k)}\right]_i, \left[\boldsymbol{D}_y \boldsymbol{u}^{(k+1)}-\boldsymbol{a}_y^{(k)}\right]_j\right)= \\ \left\{\left[\boldsymbol{v}_x^{(k+1)}\right]_i, \left[\boldsymbol{v}_y^{(k+1)}\right]_j\right\} \end{array} (9) 式中，solve表示求解，LUT表示查表，k和k+1是迭代次数。‖[vx]i2+[vy]j2‖2随迭代求解u时是一个常数，可固定不变；因为约束条件为L1，故:
\begin{array}{c} \left\{\left[\boldsymbol{v}_x^{(k+1)}\right]_i, \left[\boldsymbol{v}_y^{(k+1)}\right]_j\right\}= \\ \frac{\left\{\boldsymbol{D}_x \boldsymbol{u}^{(k)}-\left[\boldsymbol{a}_x\right]_i, \boldsymbol{D}_y \boldsymbol{u}^{(k)}-\left[\boldsymbol{a}_y\right]_j\right\}}{\left\|\left\{\boldsymbol{D}_x \boldsymbol{u}^{(k)}-\left[\boldsymbol{a}_x\right]_i, \boldsymbol{D}_y \boldsymbol{u}^{(k)}-\left[\boldsymbol{a}_y\right]_j\right\}\right\|} \times \\ \max \left(\left\|\left\{\boldsymbol{D}_x \boldsymbol{u}^{(k)}-\left[\boldsymbol{a}_x\right]_i, \boldsymbol{D}_y \boldsymbol{u}^{(k)}-\left[\boldsymbol{a}_y\right]_j\right\}\right\|-\right. \\ \left.\frac{1}{\alpha}\left\|\left[\boldsymbol{v}_x\right]_i^2+\left[\boldsymbol{v}_y\right]_j^2\right\|, 0\right) \end{array} (10) 将其记为：LUT([Dxu(k+1)－ax(k)]i, [Dyu(k+1)－ay(k)]j)。
对于图 4中的step 3.2，固定u，求解迭代模糊核矩阵：
f(\mathit{\boldsymbol{h}}) = \frac{\gamma }{2}\left\| {\mathit{\boldsymbol{Uh}} - \mathit{\boldsymbol{g}}} \right\|_2^2 + \frac{1}{\alpha }\sum\limits_{(i, j)} \mathit{\Psi } \left( {{\mathit{\boldsymbol{h}}_{ij}}} \right) (11) 式中，U是图像u的傅里叶变换。设h=vh，采用替换方法有：
f\left( {\mathit{\boldsymbol{h}}, {\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{h}}}} \right) = \frac{\gamma }{2}\left\| {\mathit{\boldsymbol{Uh}} - \mathit{\boldsymbol{g}}} \right\|_2^2 + \frac{1}{\alpha }\sum\limits_{(i, j)} \mathit{\Psi } \left( {{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{h}}}} \right) (12) 通过ALM，将上述泛函表示为：
\begin{array}{c} f\left( {\mathit{\boldsymbol{h}}, {\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{h}}}} \right) = \frac{\gamma }{2}\left\| {\mathit{\boldsymbol{Uh}} - \mathit{\boldsymbol{g}}} \right\|_2^2 + \\ \frac{1}{\alpha }\sum\limits_{(i, j)} \mathit{\Psi } \left( {{\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{h}}}} \right) + \frac{\theta }{2}{\left\| {\mathit{\boldsymbol{h}} - {\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{h}}} - {\mathit{\boldsymbol{a}}_\mathit{\boldsymbol{h}}}} \right\|^2} \end{array} (13) 式中，θ是增广拉格朗日参量; ah变量为拉格朗日乘子。设ah(0)=0, k=0，采用坐标梯度下降算法求解最优h，即：
\begin{array}{c} {\rm{solve }}\left( {{\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{U}} + \frac{\mathit{\theta }}{\gamma }\mathit{\boldsymbol{I}}} \right){\mathit{\boldsymbol{h}}^{(k + 1)}} = \\ {\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{g}} + \frac{\mathit{\theta }}{\gamma }\left[ {\mathit{\boldsymbol{v}}_\mathit{\boldsymbol{h}}^{(k)} + {\mathit{\boldsymbol{a}}_\mathit{\boldsymbol{h}}}^{(k)}} \right] \end{array} (14) 式中，I为单位矩阵。另令[vh(k+1)]i=max([h(k+1)－a(k)]－1/θ, 0)，ah(k+1)=ah(k)－h(k+1)+vh(k+1)，k=k+1。通过上述两次ALM优化，交替优化求解最优u和h。
3. 实验结果及分析
实验设计中，模糊核矩阵基本大小为10 pixel×10 pixel，根据图像统计梯度信息的L2范数总值阶梯性变化模糊核矩阵，对应关系即导引头与场景目标越近，图像细节信息越丰富，梯度信息越明显，对应的模糊核矩阵越大，模糊核矩阵分为20 pixel×20 pixel，40 pixel×40 pixel，最大为80 pixel×80 pixel；通过多次实验结果分析，迭代次数对复原结果影响不大，故本实验过程中的迭代次数选择为4, 范数约束选择1。其它参数沿用参考文献[1]，即γ=1, α=1。
分别比较Lucy-Richardson(LR)算法、KOTERA方法[1]、TV先验约束复原方法与本文作者所提出先验约束设计方法的实验结果，几类场景条件下的红外图像复原结果见图 5~图 7。从左往右依次为输入图像、LR方法处理输入图像的结果图像、KOTERA方法处理输入图像的结果图像、TV先验约束复原图像、本文中的先验约束复原图像。本文中设计的先验约束具有凸显图像边缘信息，对原始图像具有明显的图像增强效果。
![图 6 空中目标红外图像算法复原结果图]()
图 6 空中目标红外图像算法复原结果图Figure 6. Restoration results of aerial helicopter infrared images另一方面，随着研究人员的不同，主观上有一定的评判差异。本文中采用对比度增强边缘(contrast enhanced edge，CEE)统计[19]、图像像素的模糊检测累积概率(cumulative probability of blur detection，CPBD)[20]和峰值信噪比(peak signal-to-noise ratio, PSNR)来客观评价去模糊质量。CEE统计评判方法利用显著边缘检测方式获得对比图，再利用相关指标来刻画图像对比度提高程度，该值越大越好；CPBD方法从像素角度建立图像模糊概率来评价图像模糊程度，为非参考图像质量评估方法，该值越大越好；PSNR从像素方面统计计算图像复原图像与原始图像之间的差值的对数，刻画图像像素级变化，是一种较典型的图像对比方法。3种客观评估算法对实验图像的数据对比分别见表 1、表 2、表 3。本文作者提出的算法复原导引头红外图像边缘信息增加了20%~50%，PSNR提高了0.8~3.4，图像像素的模糊检测累积概率提高了0.3~0.5。
compare algorithm CEE PSNR CPBD input image 31040 27.7279 0.4086 LR 31855 29.1359 0.4194 KOTERA 33270 29.4611 0.5031 TV priori constraint 32162 29.1723 0.4636 our method 35249 30.5200 0.7699 compare algorithm CEE PSNR CPBD input image 7501 35.4843 0.2282 LR 7952 36.2828 0.3282 KOTERA 11348 37.3601 0.4787 TV priori constraint 8482 36.6806 0.4009 our method 13198 40.7413 0.7851 compare algorithm CEE PSNR CPBD input image 20983 25.7595 0.4364 LR 23168 26.1619 0.4479 KOTERA 46347 26.3511 0.4891 TV priori constraint 39027 26.3608 0.4611 our method 54777 26.4413 0.8588 复原图像的对比度增强边缘图像对比见图 8~图 10，可见用本文中的方法复原图像更加凸显边缘细节。
4. 结论
以红外图像导引头的多尺度成像与应用特性为出发点，通过分析动载体成像、多尺度成像与导引头应用场景3个方面，以梯度统计为分析手段，建立适合导引头成像处理的先验约束模型，为图像导引头的成像质量研究提供一种新思路。实验设计时，为了避免成像噪声对实验结果的影响，采用保边缘的双边滤波算法对图像噪声滤波。通过对比LR方法、KOTERA方法和TV先验约束复原结果可知，算法具有凸显图像边缘信息、增强图像细节纹理、提高图像信噪比的特点，更有利于红外图像的应用的效果。
-
![]()
图 2 清晰度较高的红外图像梯度统计信息
Figure 2. High-resolution infrared image gradient statistics result
![]()
图 3 清晰度不高的红外图像梯度统计信息
Figure 3. Low-resolution infrared image gradient statistics result
![]()
图 6 空中目标红外图像算法复原结果图
Figure 6. Restoration results of aerial helicopter infrared images
compare algorithm CEE PSNR CPBD input image 31040 27.7279 0.4086 LR 31855 29.1359 0.4194 KOTERA 33270 29.4611 0.5031 TV priori constraint 32162 29.1723 0.4636 our method 35249 30.5200 0.7699 
下载: 导出CSV
compare algorithm CEE PSNR CPBD input image 7501 35.4843 0.2282 LR 7952 36.2828 0.3282 KOTERA 11348 37.3601 0.4787 TV priori constraint 8482 36.6806 0.4009 our method 13198 40.7413 0.7851
下载: 导出CSV
-
[1] KOTERA J, FILIP S, MILANFAR P. Blind deconvolution using alternating maximum a posteriori estimation with heavy-tailed priors[C]//International Conference on Computer Analysis of Images and Patterns. Berlin, Germany: Springer Heidelberg, 2013: 59-66.
[2] CHO T S, PARIS S, HORN B K P, et al. Blur kernel estimation using the radon transform[C]//2011 IEEE Conference on Computer Vision and Pattern Recognition(CVPR). Colorado, USA: IEEE, 2011: 241-248.
[3] 廖永忠, 蔡自兴, 何湘华. 快速运动模糊图像盲解卷积算法[J]. 光学精密工程, 2013, 21(10): 2688-2695. https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM201310029.htm LIAO Y Zh, CAI Z X, HE X H. Fast algorithm for motion blurred image blind deconvolution[J]. Optics and Precision Engineering, 2013, 21(10): 2688-2695(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM201310029.htm
[4] 王国栋, 徐洁, 潘振宽, 等. 基于归一化超拉普拉斯先验项的运动模糊图像盲复原[J]. 光学精密工程, 2013, 21(5): 1340-1348. https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM201305033.htm WANG G D, XU J, PAN Zh K, et al. Blind image restoration based on normalized hyper Laplacian prior term[J]. Optics and Precision Engineering, 2013, 21(5): 1340-1348(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM201305033.htm
[5] PAN J S, SUN D, PFISTER H, et al. Deblurring images via dark channel prior[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(10): 2315-2328. DOI: 10.1109/TPAMI.2017.2753804
[6] 唐述, 万盛道, 杨书丽, 等. 空间尺度信息的运动模糊核估计方法[J]. 软件学报, 2019, 30(12): 3876-3891. https://www.cnki.com.cn/Article/CJFDTOTAL-RJXB201912020.htm TANG Sh, WAN Sh D, YANG Sh L, et al. Spatial-scale-information method for motion blur kernel estimation[J]. Journal of Software, 2019, 30(12): 3876-3891(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-RJXB201912020.htm
[7] 余孝源, 谢薇, 陈定权, 等. 一种基于改进的暗通道先验的运动模糊核估计方法[J]. 控制与决策, 2020, 35(7): 1667-1673. https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC202007016.htm YU X Y, XIE W, CHEN D Q, et al. A method of motion blurry kernel estimation based on improved dark channel prior[J]. Control and Decision, 2020, 35(7): 1667-1673(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC202007016.htm
[8] 贾平, 张葆, 孙辉. 航空成像像移模糊恢复技术[J]. 光学精密工程, 2006, 14(4): 697-703. DOI: 10.3321/j.issn:1004-924X.2006.04.030 JIA P, ZHANG B, SUN H. Restoration of motion-blurred aerial image[J]. Optics and Precision Engineering, 2006, 14(4): 697-703(in Chinese). DOI: 10.3321/j.issn:1004-924X.2006.04.030
[9] YU W T, PING T, MICHAEL S B. Richardson-Lucy deblurring for scenes under a projective motion path[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1603-1818. DOI: 10.1109/TPAMI.2010.222
[10] KRISHNAN D, TAY T, FERGUS R. Blind deconvolution using a normalized sparsity measure[C]//2011 IEEE Conference on Computer Vision and Pattern Recognition. Colorado, USA: IEEE, 2011: 233-240.
[11] LEVIN A, WEISS Y, DURAND F, et al. Understanding blind deconvolution algorithm[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2011, 33(12): 2354-2367.
[12] SUN L, CHO S, WANG J, et al. Edge-based blur kernel estimation using patch priors[C]//2013 IEEE International Conference on Computational Photography(ICCP). Cambridge, USA: IEEE, 2013: 1-8.
[13] 李伟红, 董亚莉, 唐述. 多范数混合约束的正则化图像盲复原[J]. 光学精密工程, 2013, 21(5): 1357-1364. https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM201305035.htm LI W H, DONG Y L, TANG Sh. Regularized blind image restoration based on muli-norm hybrid constraints[J]. Optics and Precision Engineering, 2013, 21(5): 1357-1364(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM201305035.htm
[14] CHEN L, FANG F, LEI S, et al. Enhanced sparse model for blind deblurring[C]//2020 European Conference on Computer Vision(ECCV). Berlin, Germany: Springer Heidelberg, 2020: 631-646.
[15] CHO S, LEE S. Convergence analysis of MAP based blur kernel estimation[C]//2017 IEEE International Conference on Computer Vision(ICCV). Venice, Italy: IEEE, 2017: 4818-4826.
[16] YANG L, JI H. A variational EM framework with adaptive edge selection for blind motion deblurring[C]//2019 IEEE Conference on Computer Vision and Pattern Recognition(CVPR). Long Beach, USA: IEEE, 2019: 10159-10168.
[17] 余博, 郭磊, 赵天云, 等. 红外图像的自适应混合双边滤波算法[J]. 红外与激光工程, 2012, 41(11): 3102-3107. https://www.cnki.com.cn/Article/CJFDTOTAL-HWYJ201211047.htm YU B, GUO L, ZHAO T Y, et al. Adaptive hybrid bilateral filtering algorithm for infrared image[J]. Infrared and Laser Engineering, 2012, 41(11): 3102-3107(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HWYJ201211047.htm
[18] 郭佩瑜, 张宝华. 基于引导滤波和模糊算法的红外背景抑制算法[J]. 激光技术, 2018, 42(6): 854-858. DOI: 10.7510/jgjs.issn.1001-3806.2018.06.024 GUO P Y, ZHANG B H. Infrared background suppression algorithm based on guided filtering and fuzzy algorithm[J]. Laser Technology, 2018, 42(6): 854-858(in Chinese). DOI: 10.7510/jgjs.issn.1001-3806.2018.06.024
[19] HAUTIERE N, TAREL J P, AUBERT D, et al. Blind contrast enhancement assessment by gradient rationing at visible edges[J]. Image Analysis & Stereology Journal, 2008, 27(2): 87-95.
[20] NIRANJAN D N, LINA J K. A no-reference image blur metric based on the cumulative probability of blur detection(CPBD)[J]. IEEE Transactions on Image Processing, 2011, 20(9): 2678-2683.
-
期刊类型引用(1)
1. 李丰，李燕，石彬彬. 加权高斯匹配滤波下激光复合成像三维重构. 激光杂志. 2025(01): 251-256 . 
百度学术
其他类型引用(0)
计量
- 文章访问数: 5
- HTML全文浏览量: 1
- PDF下载量: 5
- 被引次数: 1