Multiple-color-image compression and encryption by using discrete wavelet transform in Fresnel transform domain
-
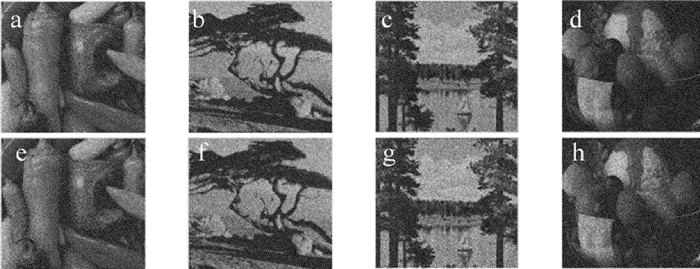
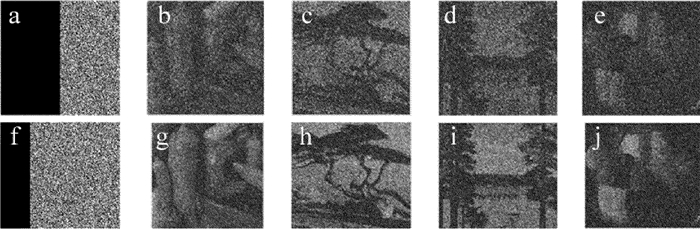
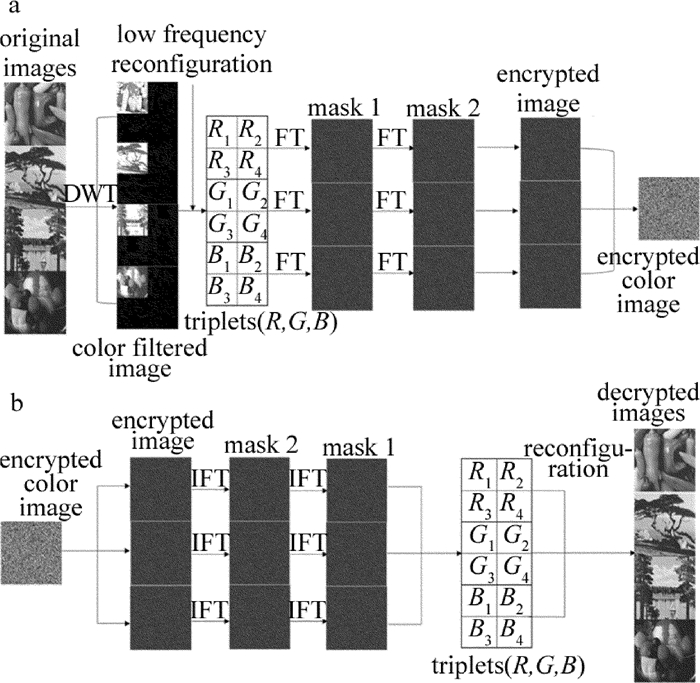
摘要: 为了解决多彩色图像加密后，解密图像质量不佳、数据量大以及传输时速率慢的问题，采用了一种基于小波变换和菲涅耳变换的多彩色图像加密方法，加密过程中，利用小波变换的多级分解特性提取每幅彩色图像的低频分量，将低频分量分别重组为三元组图像（R，G和B），并且依次将三元组图像（R，G和B）通过菲涅耳域中的衍射加密系统，对这3个三元组图像进一步加密，从而实现了多彩色图像的加密。结果表明，该方法不仅可以高质量地恢复原始彩色图像，而且可以同时对4幅彩色图像进行加密，提高了加密彩色图像的容量；原始图像经过小波变换，其数据量压缩到原来的1/4，有利于数据的传输和存储。该算法能够有效地同时对多幅色彩图像进行压缩和加密，不仅提高了解密图像的质量，并且具有较高的密钥敏感度和较好的鲁棒性。Abstract: In order to solve the problems of the low quality of image, the large amount of data and the slow rate of transmission, an optical compression and encryption method of multiple-color images by using discrete wavelet transform in Fresnel transform domain had been proposed. In the process of encryption, the low-frequency components of each color image were extracted by using the multilevel decomposition characteristics of wavelet transform, and the low frequency components were reorganized to triplet images (R, G and B), respectively. And the triplet images (R, G and B) were sequentially encrypted through the diffraction encryption system in the Fresnel domain. After triplet images were further encrypted, the encryption of multi-color images was realized. The results show that, the method can not only reconstruct the original color image with high quality, but also encrypt 4 color-images at the same time, which increases the capacity of the encrypted color image. The data volume of the encryption is compressed 1/4 after wavelet transform, which is beneficial to the transmission and storage of the data. The algorithm can effectively compress and encrypt multiple-color images at the same time. It not only improves the quality of the decrypted image, but also has high key sensitivity and good robustness.
-
-
![]()
Figure 6. Gray-level histograms and auto-correlation pictures before and after encryption
Table 1 Cxy values of the decrypted images
Cxy values peppers tress lake fruits the proposal 0.9939 0.9960 0.9833 0.9974 reference [18] 0.9411 0.8746 0.8512 0.8574 
下载: 导出CSV
Table 2 Cxy values of the decrypted images after noise
salt-and-pepper noise with different stand deviation Cxy values of decrypted images pepper tress lake fruits k=0.8 0.9180 0.9592 0.9538 0.9424 k=1 0.9035 0.9526 0.9470 0.9345
下载: 导出CSV
Table 3 Cxy values of the corresponding decrypted images after occlusion
occlusion of the encrypted image/% Cxy values of decrypted images pepper tress lake fruits 25% 0.6525 0.7702 0.7606 0. 7082 50% 0.3943 0.5383 0.5137 0.4685
下载: 导出CSV
-
[1] JAVIDI B, REFREGIER P. Optical image encryption based on input plane and Fourier plane random encoding[J]. Optics Letters, 1995, 20(7):767-769. DOI: 10.1364/OL.20.000767
[2] QIAO J P, DENG L W, HE J, et al. Optimization of fast image encryption algorithm based on chaotic mapping[J]. Laser Technology, 2017, 41(6):897-897(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs201706026
[3] LIU Z, LI S, LIU W, et al. Image encryption algorithm by using fractional Fourier transform and pixel scrambling operation based on double random phase encoding[J]. Optics and Lasers in Engineering, 2013, 51(1):8-14. DOI: 10.1016/j.optlaseng.2012.08.004
[4] JOSHI M, CHANDRASHAKHER, SINGH K. Color image encryption and decryption using fractional Fourier transform[J]. Optics Communications, 2007, 279(1):35-42. DOI: 10.1016/j.optcom.2007.07.012
[5] LIU H, WANG X. Color image encryption using spatial bit-level permutation and high-dimension chaotic system[J]. Optics Communications, 2011, 284(16):3895-3903. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0221800390/
[6] WANG P, YUAN C J, WANG L, et al. Encryption and decryption for double images based on fractional Fourie transformation[J]. Laser Technology, 2014, 38(4):551-555(in Chinese) http://en.cnki.com.cn/Article_en/CJFDTotal-JGJS201404023.htm
[7] SITU G, ZHANG J. Double random-phase encoding in the Fresnel domain[J]. Optics Letters, 2004, 29(14):1584-1586. DOI: 10.1364/OL.29.001584
[8] CHEN L, ZHAO D. Optical color image encryption by wavelength multiplexing and lensless Fresnel transform holograms[J]. Optics Express, 2006, 14(19):8552-8560. DOI: 10.1364/OE.14.008552
[9] ABUTURAB M R. Optical interference-based multiple-image encryption using spherical wave illumination and gyrator transform[J]. Applied Optics, 2014, 53(29):6719-6728. DOI: 10.1364/AO.53.006719
[10] CHEN W. Optical multiple-image encryption using three-dimensional space[J]. IEEE Photonics Journal, 2016, 8(2):1-8. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0223029814/
[11] YUEN C H, WONG K W. A chaos-based joint image compression and encryption scheme using DCT and SHA-1[J]. Applied Soft Computing, 2011, 11(8):5092-5098. DOI: 10.1016/j.asoc.2011.05.050
[12] SHI X, ZHAO D, HUANG Y, et al.Multiple color images encryption by triplets recombination combining the phase retrieval technique and Arnold transform[J]. Optics Communications, 2013, 306:90-98. DOI: 10.1016/j.optcom.2013.05.041
[13] LIN C, WANG J G, MA W P, et al. Study on chaotic encryption algorithm for images after compression[J]. Microelectronics and Computer, 2013, 30(3):5-7(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=wdzxyjsj201303004
[14] XU G X, XU S Q, GUO X J, et al.Image compression-encryption algorithm combined DCT transform with DNA operation[J]. Laser Technology, 2015, 39(6):806-810(in Chinese). http://www.opticsjournal.net/abstract.htm?aid=OJ151130000298WtZv3y
[15] MEHRA I, NISHCHAL N K. Wavelet-based image fusion for securing multiple images through asymmetric keys[J]. Optics Communications, 2015, 335:153-160. DOI: 10.1016/j.optcom.2014.09.040
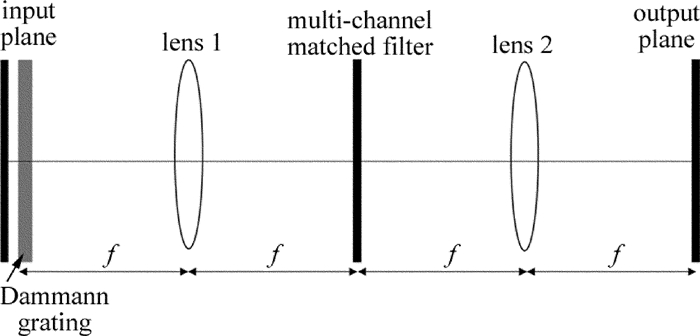
[16] MENDLOVIC D, OUZIELI I, KIRYUSCHEV I, et al. Two-dimensional wavelet transform achieved by computer-generated multireference matched filter and Dammann grating[J]. Applied Optics, 1995, 34(35):8213-8219. DOI: 10.1364/AO.34.008213
[17] MENDLOVIC D, KONFORTI N. Optical realization of the wavelet transform for two-dimensional objects[J]. Applied Optics, 1993, 32(32):6542-6546. DOI: 10.1364/AO.32.006542
[18] QIN Y, WANG Z, PAN Q, et al. Optical color-image encryption in the diffractive-imaging scheme[J]. Optics and Lasers in Engineering, 2016, 77:191-202. DOI: 10.1016/j.optlaseng.2015.09.002
-
期刊类型引用(2)
1. 秦树旺，毛耀，包启亮. 光电跟踪系统的模糊Ⅱ型控制技术研究. 激光技术. 2021(02): 147-154 . 
本站查看
2. 郑羽，李东，王艳林. 基于FPGA的精密指向组件控制系统设计. 工业控制计算机. 2019(07): 12-14+17 . 百度学术
其他类型引用(3)
计量
- 文章访问数: 5
- HTML全文浏览量: 0
- PDF下载量: 9
- 被引次数: 5