Research on wavelength calibration technology for visible spectral radiometer
-
摘要: 为了解决可见光光谱辐射计波长标定过程中存在的峰值偏移、较弱特征谱误判及人工谱线识别等问题,采用自适应阈值法和差分法完成对特征谱检测与识别,利用最小二乘法和拉格朗日插值法确定波长和像元的关系,进行了理论分析和实验验证,获得最佳波长标定方程。结果表明,特征谱根据谱线强度依次被检测并识别出来,以404.6565 nm、435.8335 nm、546.0750 nm、579.0670 nm为基准的拉格朗日插值法得到的方程为最佳波长标定方程,其残差标准差仅为3.2747×10-13nm,波长标定误差分布在±0.2 nm范围内。自动谱线检测方法及谱线识别方法提高了波长标定效率,避免了噪声误判和谱线识别错误现象,为其它光谱类仪器的波长标定提供了参考。Abstract: In order to solve the problems of peak shift, weak feature spectrum misjudgment, and artificial spectral line recognition in the wavelength calibration process of visible light spectroradiometers, the adaptive threshold method and the differential method were used to detect and recognize the feature spectrum. Meanwhile, the relationship between wavelength and pixel was determined using the method of least squares and Lagrange interpolation. Theoretical analysis and experimental verification were carried out and the optimum wavelength calibration equation was obtained. The results show that the feature spectrum is detected and recognized sequentially based on the intensity of the spectral lines. The optimal equation was obtained by the Lagrange interpolation method based on 404.6565 nm, 435.8335 nm, 546.0750 nm, and 579.0670 nm, with a residual standard deviation of only 3.2747×10-13nm, the wavelength calibration error distribution is within the range of ±0.2 nm. Therefore, this method improves the efficiency of wavelength calibration. It also avoids noise misjudgment and spectral line recognition error and provides reference for wavelength calibration of other spectral instruments.
-
0. 引言
光谱辐射计是在光学领域中的一类重要检测仪表, 在野外观测、海洋光学以及科研等领域中都发挥了巨大的作用。光谱辐射计可以在比较窄的光谱区域中, 对目标的光谱辐射通量进行检测。光谱辐射计根据工作波长分为紫外光谱辐射计、红外光谱辐射计和可见光光谱辐射计[1-4]。
光谱辐射计必须进行波长标定,否则将无法获得被测光源的光谱辐射强度分布曲线[5-6]。对于光谱辐射计,通常采用理论推导法和波长标定实验法[7]两种方法进行波长标定。理论推导法是根据光谱辐射计的光学结构利用光栅方程来推导出波长与像元之间的对应关系;波长标定实验法是使用光谱辐射计采集标准光源特征谱,借助算法确定各特征谱在电荷耦合器件(charge-coupled device, CCD)上的位置,并采用数学方法根据已知数据获得波长与像素位置的关系,从而通过计算得到每个像素位置相应的波长[8]。然而受零件加工和安装误差的影响,基于光栅衍射原理的理论推导法存在较大误差。因此,多采用波长标定实验法对光谱辐射计进行波长标定。
目前,学者们对波长标定实验法已经进行了大量的研究。WU等人[9]利用最小二乘拟合法完成了光谱仪的波长标定,虽然其波长标定误差仅为0.15 nm,但没有将标准光谱仪自身的波长标定精度考虑进去。DONG等人[10]通过逐次分析残差分布对波长标定进行了研究,拟合残差基本上分布在±0.5 nm以内,虽然在直接极值法的基础上引入多次平均处理,但是无法解决峰值偏移问题。LI等人[11]分析了波长标定过程中3个关键因素,即标准灯的选择、谱线质心确定及拟合级次对波长标定精度的影响,拟合误差小于0.5 nm,虽然提高了波长标定精度,但是需要借助于人工判断特征峰的波长。对于自动波长标定,QIN等人[12]通过预先设置自适应阈值并通过迭代确定了郭守敬望远镜(large sky area multi-object fiber spectroscopy telescope,LAMOST)发射线的质心,但是采用谱线强度对特征谱线识别使得实际使用时出现谱线识别错误问题。MA等人[13]使用自动分解算法,将重叠峰分解成单峰来消除重叠峰对于发射线质心确定的影响,然后使用线状谱模型优化了特征谱的形状,从而获得每个发射线质心的位置,标定精度达到了0.1 nm。该方法消除了仪器带宽和噪声的影响,但是对波长与像元关系拟合研究较少。
针对上述问题,本文作者将自动波长标定法应用到光谱辐射计的标定中,基于LAMOST动态检测思想,采用自适应阈值法对特征谱进行自动检测,同时对谱线识别算法进行改进,使用差分法代替相对强度法对特征谱进行自动识别。
1. 自适应阈值波长标定
为了建立波长和像元位置的数学模型,使用光谱辐射计采集标准光源的光谱分布,随后利用寻峰算法获得已知特征谱的像素位置,并根据已知波长和像元位置数据建立两者之间的数学模型。图 1所示为自适应阈值波长标定流程图。
1.1 光谱预处理
受CCD暗电流噪声、电路热噪声等因素的影响,光谱辐射计采集到的光谱曲线通常会变得不平滑[14-17]。
为了减小随机误差,对光谱数据测量20次后取算术平均值。但在算数平均处理后,每个特征峰上仍存在“毛刺”而影响后续特征峰的检测。为了避免这些“毛刺”对峰值检测的干扰,采用高斯加权移动平均滤波器对平均处理后的光谱数据进行处理。
高斯加权移动平均滤波器是加权移动平均滤波器一种。加权移动平均滤波器是使用一个权重向量对窗口内的样本进行加权平均,权重向量决定了每个样本在平均计算中的重要性,而高斯加权移动平均滤波器的权重是利用高斯分布函数计算得到的,距离样本越近,权重越大,距离样本越远,权重越低。高斯加权移动平均滤波器的数学模型[18]为:
<italic>g</italic>(<italic>i</italic>)=ωi−(N−1)/2yi−(N−1)/2+⋯+ωi−1yi−1+ωiyi+ωi+1yi+1+⋯+ωi+(N−1)/2yi+(N−1)/2ωi−(N−1)/2+⋯+ωi−1+ωi+ωi+1+⋯+ωi+(N−1)/2 (1) 式中:N为窗口长度(N为奇数);g(i)为第i个像元处的移动平均值;ωi为第i个像元处的权重,ωi=exp[-(i-c)2/(2s2)];yi表示噪声处理前的第i个像元处的谱线强度;c是当前时间点;s为高斯函数的标准差。
高斯加权移动平均滤波器可以在去除高斯噪声的同时尽可能地保留信号原始特征。每一个独立的特征峰在数学上符合高斯分布,同时每个特征峰上的局部噪声也是高斯噪声,因此对局部噪声进行高斯加权移动平均滤波不仅可以去除噪声,而且也不会改变特征峰的原始特征。图 2所示为采用高斯加权移动平均滤波器的噪声处理前后效果图。
根据图 2可以观察到,特征峰上的局部“毛刺”已经变光滑,同时曲线的原始特征也被很好的保留。
对于理想光源,其连续谱基本为零,整个光谱的均值近似为零,所以特征谱的标准差与整个标定光源的标准差近似相等;但对于实际光源,受自身气压、温度、各种环境因素以及人为因素的影响,实际测试得到的标准光源连续谱不为零,为了便于后续特征谱的检测,对噪声处理后的光谱数据进行零均值化处理(即将每个像素对应的电信号强度减去所有谱线强度的平均值),处理后整个标定光源的均值近似为零。
1.2 特征谱检测
对于一个标准光源,不同特征谱的强度存在明显差异,如果采用固定阈值检测可能会出现较弱特征谱被丢弃或者噪声被误认为特征谱的问题。为了避免固定阈值带来的问题,本文中借鉴LAMOST中的自适应阈值法[12]进行特征谱检测。通过预先设置自适应阈值并执行迭代定位来进行特征谱检测。特征谱线相当于一个一个的脉冲信号,为了实现特征谱的动态检测,采用特征谱的标准差作为自适应阈值。但是直接计算特征谱的标准差较为复杂,而计算整个光谱的标准差比较简单,因此需要建立两者的关系。根据第1.1节,对整个标定光源的谱线进行零均值化处理后,其均值近似为零,则整个标定光源谱线的标准差与特征谱线的标准差存在以下关系:
σ=√P∑i=1(Ei−ˉE)2P≈√P∑i=1Ei2P≈√Q∑j=1F2jQ (2) 式中:Ei为噪声处理后的第i个像元处的谱线强度;E为噪声处理后的整个标定光源的谱线强度均值;P为探测器像元数目;Fj为噪声处理后的第j条特征谱的强度;Q为整个标定光源的特征谱数目;σ为整个标定光源谱线的标准差(谱线强度是指探测器将光信号转换为电压后,经过模数转换后的数字量化值,表示电信号的强度值)。
根据式(2),特征谱线的标准差与整个标定光源的标准差存在近似相等的关系。因此,本文中利用标准光源的标准差作为自适应阈值对特征谱进行动态检测。首先计算采集到的光谱数据的标准差,并将阈值设定为3σ,以检测出信号大于3σ的谱线;然后利用极值法确定已检测出的特征谱质心和边界,并删除首次检测出的谱线,重新计算标准差,将阈值设定为新的3σ,继续检测,直至检测出的特征谱线数量达到光源标准谱线表中的要求。对动态检测出的特征谱线,在极值峰位检测的基础上进行高斯拟合,进一步确定亚像素级的像元位置。
分析可知,在特征谱的迭代检测过程中,每一次迭代,谱线强度大于阈值的特征谱均会被检测出来,阈值随着迭代过程不断减小,不同特征谱根据强度大小依次被检测出来。当检测出的特征谱线数目满足要求时,停止检测,避免了较弱特征谱被误认为噪声的现象。
1.3 特征谱识别
为了建立波长和像元位置的数学关系,需要对动态检测出的特征谱进行识别。对于采集到的光谱数据,QIN等人[12]利用色散曲线的局部线性特性和特征谱线相对强度的局部线性特性对特征谱线进行识别。但实际中受电路热噪声及CCD暗电流噪声的影响,光谱辐射计采集到的不同特征谱强度发生明显变化,使得不能利用特征谱线相对强度的局部线性关系进行谱线识别。本文中根据光栅的色散线性特征进行特征谱识别。平面光栅的衍射方程[19]如下式所示:
d(sinα±sinβ)=mλ (3) 式中:d为光栅常数;α和β分别为光线到达光栅的入射角与衍射角;m为衍射级次,光谱辐射计通常取1级衍射光谱;λ为不同衍射角对应的波长。
根据光栅衍射方程,波长和像元位置在总体上近似呈线性关系。通过差分法获得像素间距最大的两个特征峰作为初始谱线来进行改进。在改进的方法中,首先利用1阶差分计算相邻峰的像素距离,最大的相邻峰像素距离对应于相邻波长差异最大的两个特征波长,将这两个波长作为初始谱线识别结果,记录其波长和像素位置;然后对于迭代检测出的特征峰,根据其像素位置与初始谱线像素位置的差异对剩余特征谱线进行迭代识别。
初始谱线识别是后续迭代谱线识别的基础。为了从所有特征谱线中首先识别出两个特征峰,从光栅色散的近似线性特征考虑,理论谱线表中相邻特征谱波长差异最大的两个波长分别对应实际所测特征峰位置差异最大的两个波长。基于此原理,利用1阶差分法实现初始谱线识别。
对标准光源理论谱线表中的特征波长和检测出的特征峰计算以下参数:
{Y=[λ(2)−λ(1),λ(3)−λ(2),⋯,λ(n)−λ(n−1)]Δλmax (4) 式中:Y为元素是相邻特征波长之间的差分;X为相邻特征谱位置间的差分;n为特征峰数量;λ(n)表示第n个特征峰的波长;x(n)表示第n个特征峰的像元位置;Δλmax和Δxmax分别表示波长差分最大值和位置差分最大值;a和b分别对应于Δλmax和Δxmax在Y和X中的元素序号;(xa, λb)和(xa+1, λb+1)为初始谱线识别结果。
迭代谱线识别是利用初始谱线识别的结果,对剩余的谱线依次进行识别。对于动态检测出的特征峰,分别计算其像素位置与初始谱线像素位置的差异,通过对比其位置差异与标准波长差异的大小依次对剩余特征谱线进行迭代识别。采用差分法对特征谱进行识别是基于波长和像元位置在总体上的近似呈线性关系原理,避免了采用谱线强度对特征谱识别而出现的谱线识别错误问题。
1.4 波长标定方程的确定
寻找波长和像元位置之间的关系, 就是根据已知特征波长及其像元位置数据求出其近似关系。为了获得这种近似关系,通常采用插值法和拟合法。插值和拟合的区别在于插值要求所有数据必须都在曲线上,而拟和没有要求所有的数据必须在曲线上,只要求能够反映数据的基本趋势[20]。本文中分别采用插值和拟合的方法来获得波长和像元位置之间的映射关系。
2. 标定实验
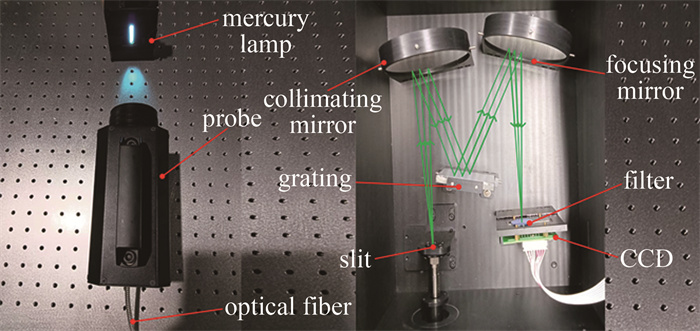
本文中的研究内容为可见光光谱辐射计波长标定技术,实验原理如图 3所示。整个系统主要由探头、低压汞灯、狭缝、聚焦镜、光栅、准直镜、滤光片、线阵CCD等组成。
图 4所示为标定实验装置。测量时,探头对光源进行瞄准,光源发出的光通过光纤进入狭缝后到达准直物镜,准直物镜对来自狭缝的发散光进行准直形成平行光,随后平行光到达光栅,光栅对其进行色散分光形成单色光后照射在聚焦镜上,光束最终经聚焦镜会聚到达探测器。其中,探测器上的滤光片用于滤除高级衍射光谱。探测器进行光电转换,并通过网线接口将采集到的原始信号传输至上位机。表 1所示为各器件具体参数。
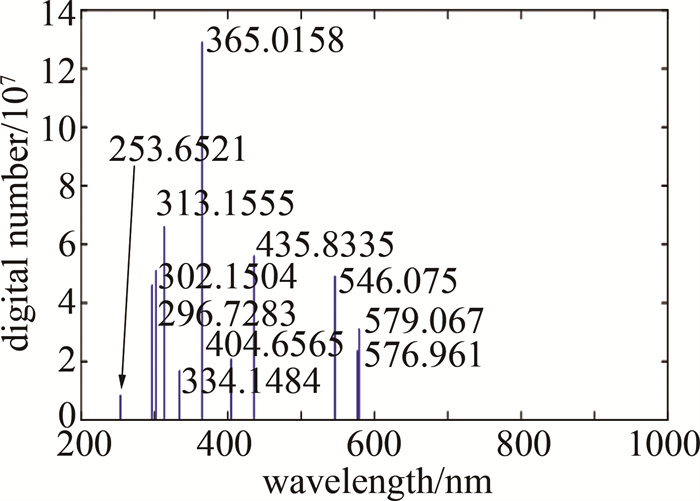
表 1 各器件具体参数Table 1. Specific parameters of each deviceitem parameters mercury lamp type:LHM254 probe(camera lens) focal length:50 mm collimating mirror focusing mirror radius:300 mm focal length:150 mm CCD 8 μm×200 μm, number of pixels:3648 grating lines:300 lp/mm size:50 mm×50 mm blaze wavelength:500 nm slit 0.1 mm 对于标准光源,其特征峰波长应该覆盖在光谱辐射计的工作波长范围内,同时谱线间隔应该大于光学系统的分辨率,否则谱线将不能被分辨。本文中使用的低压汞灯有11条特征峰,图 5所示为汞灯标准线谱[21],适用于250 nm~1000 nm范围的波长标定。特征波长分别为253.6521 nm,296.7283 nm,302.1504 nm,313.1555 nm,334.148 nm,365.0158 nm,404.6565 nm,435.8335 nm,546.0750 nm,576.9610 nm和579.0670 nm。其中有6个特征峰不在可见光光谱辐射计的工作波段,不参与波长标定,剩余5个特征峰均能够被分辨。参与波长标定的特征波长分别为404.6565 nm,435.8335 nm,546.0750 nm,576.9610 nm和579.0670 nm。
搭建好实验平台后完成对汞灯预热,将CCD与计算机连接,调节光路和积分时间使CCD能够采集到光源的5条特征谱。为了减小随机误差的干扰,对汞灯光谱数据采集20组并求均值。
3. 结果与讨论
3.1 谱线检测结果
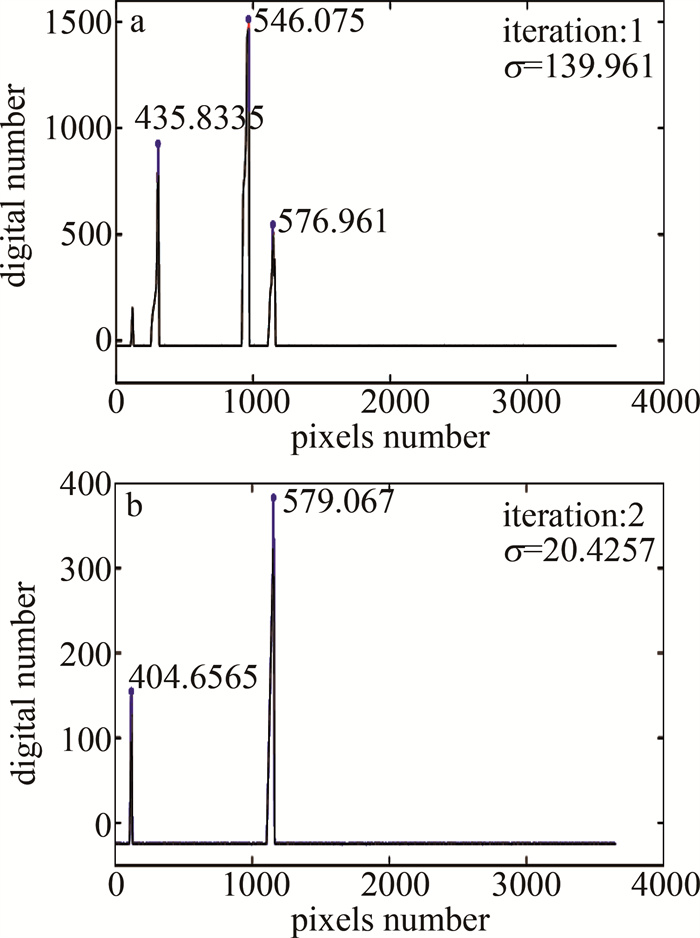
根据第1节中迭代的谱线检测算法,迭代过程中依次检测出的特征谱线如图 6a、图 6b所示。
根据图 6可以观察到,标准光源的特征谱线根据信号大小依次被检测出来,从而有效地防止了把微小噪声误判为特征峰的现象。由于直接极值峰位判定是采用搜寻曲线的局部极大值确定特征峰像素位置,而高斯拟合峰位判定是在局部极值法的基础上,对每个特征峰在其边界范围内左右依次取n个像素数据进行高斯拟合定位,并利用拟合误差逐次确定高斯拟合像素点的数目,因此存在较大噪声时,拟合的峰位也与真实峰位十分接近。最终确定对极值法检测出的峰位,左右依次取4个像素数据进行高斯拟合定位。表 2所示为特征波长及两种峰位判断方法对应的峰值位置。
表 2 各特征波及两种峰位判断方法对应的峰值位置Table 2. Characteristic wavelength and peak positions for different methodsserial number characteristic wavelength/nm pixel position Gaussian position 1 404.6565 119 119.6208 2 435.8335 306 306.1324 3 546.0750 967 965.9072 4 576.9610 1143 1143.7210 5 579.0670 1156 1155.6497 3.2 波长标定方程及精度评估
传统的波长标定方法采用基于最小二乘原理的多项式拟合法来获得波长和像元位置的关系,但数学中插值与拟合均能够获得数据间的近似关系。本文中将在多项式拟合法的基础上引入拉格朗日插值法,分别采用拟合和插值两种方法来获得波长标定方程,通过精度评估以确定最佳波长标定方程。
3.2.1 最小二乘拟合
对于高阶多项式,多项式次数增加会提高精度,但是随着多项式次数的增加拟合结果反而越偏离原函数[22]。因此需要从低到高逐次比较残差分布特性确定拟合级次。
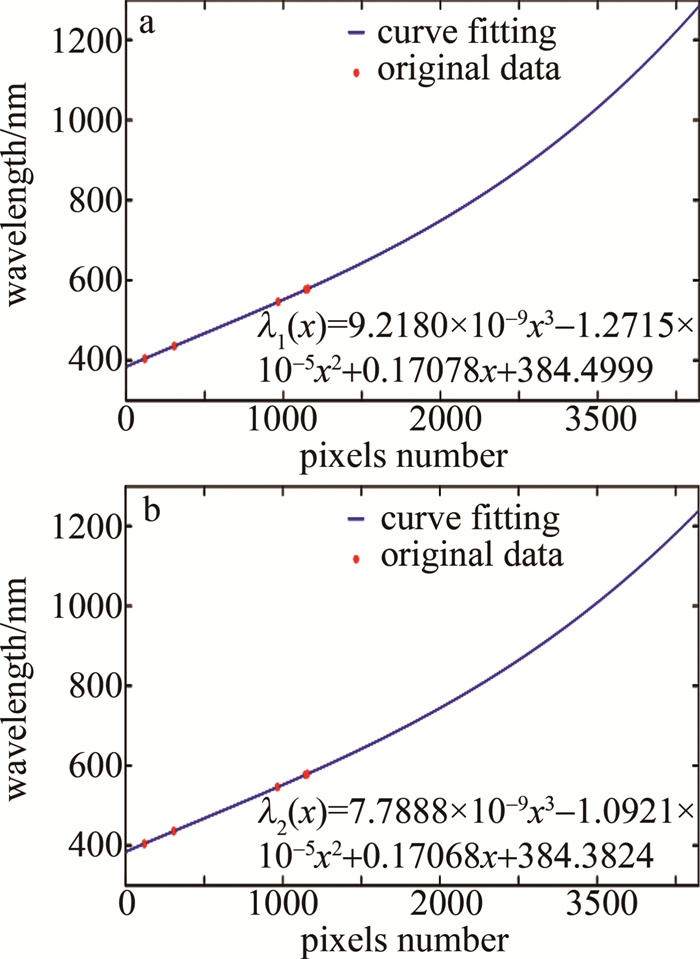
在确定多项式拟合级次时,通过逐步比较分析残差分布特性,最终确定拟合级次为3。当拟合级次超过3时,残差水平反而增加。图 7所示为直接极值峰位判定和高斯拟合峰位判定的最小二乘拟合结果。
图 7中给出了直接极值峰位判定与高斯拟合峰位判定波长标定方程。二者的3次多项式拟合方程分别为:
\begin{gathered} \lambda_1(x)=9.2180 \times 10^{-9} x^3-1.2715 \times \\ 10^{-5} x^2+0.17078 x+384.4999 \end{gathered} (5) \begin{gathered} \lambda_2(x)=7.7888 \times 10^{-9} x^3-1.0921 \times \\ 10^{-5} x^2+0.17068 x+384.3824 \end{gathered} (6) 相邻两像素的波长间隔计算公式[23]如下式所示:
\Delta \lambda=\left(\lambda_{\text {end }}-\lambda_1\right) /\left(x_{\text {end }}-x_1\right) (7) 式中:Δλ表示相邻像素的波长间隔;λ1为第1个特征峰的波长;λend为最后一个特征峰的波长;x1为第1个特征峰的像元位置;xend为最后一个特征峰的像元位置。
表 3所示为直接极值定位最小二乘拟合和高斯拟合定位最小二乘拟合残差数据。
表 3 最小二乘法残差分布及标准差Table 3. Residual distribution and mean squared error for the least squares methodmethod residual/nm mean squared error/nm direct peak position detection ±0.1097 0.06642 Gaussian fitting peak position detection ±5.86×10-4 3.5578×10-4 由表 3可知,采用最小二乘拟合法,直接极值峰位判定和高斯拟合峰位判定的残差分别为±0.1097 nm,±5.86×10-4nm。采用式(7)计算相邻两像素波长间隔为0.17 nm,并利用残差标准差对波长标定不确定度进行评估,两种峰位检测方法的残差标准差分别为0.06642 nm和3.5578×10-4nm,其中高斯拟合峰位判定的残差标准差仅为直接极值峰位判定的1/186。因此针对最小二乘拟合,采用高斯拟合定位作为波长标定方程。对波长标定不确定度进行评估:在包含因子k=1时,波长标定不确定度为u≈3.5578×10-4nm,波长标定可靠度水平为68%;在包含因子k=2时,波长标定不确定度为u=2×3.5578× 10-4nm≈7.1556×10-4nm,波长标定可靠度水平为95%。利用最小二乘法最终确定的波长标定方程如式(6)所示。
3.2.2 拉格朗日插值
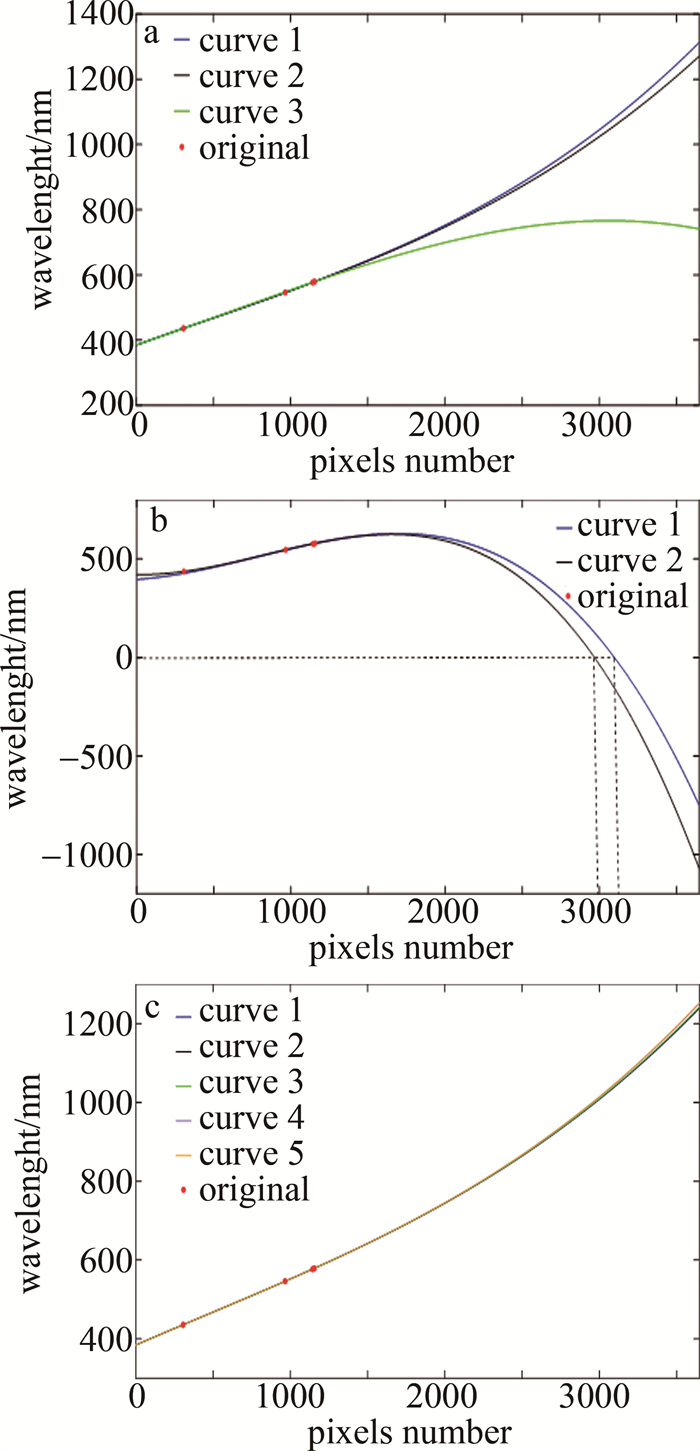
根据第3.2.1小节中确定的多项式为3次多项式,对于3次多项式,需要4个数据节点。本次波长标定共有5个数据点,分别为: λ1、λ2、λ3、λ4、λ5,共有C51=5种组合。图 8a和图 8b所示为直接极值峰位判定的不同波长组合的拉格朗日插值多项式结果;图 8c为高斯拟合峰位判定的不同波长组合的拉格朗日插值多项式结果。
![图 8 拉格朗日多项式插值结果 a—直接极值峰位判定:λ1λ2λ3λ4,λ1λ2λ3λ5,λ1λ2λ4λ5 b—直接极值峰位判定:λ1λ3λ4λ5,λ2λ3λ4λ5 c—高斯拟合峰位判定:λ1λ2λ3λ4,λ1λ2λ3λ5,λ1λ2λ4λ5,λ1λ3λ4λ5,λ2λ3λ4λ5]() 图 8 拉格朗日多项式插值结果 a—直接极值峰位判定:λ1λ2λ3λ4,λ1λ2λ3λ5,λ1λ2λ4λ5 b—直接极值峰位判定:λ1λ3λ4λ5,λ2λ3λ4λ5 c—高斯拟合峰位判定:λ1λ2λ3λ4,λ1λ2λ3λ5,λ1λ2λ4λ5,λ1λ3λ4λ5,λ2λ3λ4λ5Figure 8. Results of Lagrange polynomial interpolation a—direct peak position detection: λ1λ2λ3λ4, λ1λ2λ3λ5, λ1λ2λ4λ5 b—direct peak position detection: λ1λ3λ4λ5, λ2λ3λ4λ5 c—Gaussian fitting peak position detection: λ1λ2λ3λ4, λ1λ2λ3λ5, λ1λ2λ4λ5, λ1λ3λ4λ5, λ2λ3λ4λ5
图 8 拉格朗日多项式插值结果 a—直接极值峰位判定:λ1λ2λ3λ4,λ1λ2λ3λ5,λ1λ2λ4λ5 b—直接极值峰位判定:λ1λ3λ4λ5,λ2λ3λ4λ5 c—高斯拟合峰位判定:λ1λ2λ3λ4,λ1λ2λ3λ5,λ1λ2λ4λ5,λ1λ3λ4λ5,λ2λ3λ4λ5Figure 8. Results of Lagrange polynomial interpolation a—direct peak position detection: λ1λ2λ3λ4, λ1λ2λ3λ5, λ1λ2λ4λ5 b—direct peak position detection: λ1λ3λ4λ5, λ2λ3λ4λ5 c—Gaussian fitting peak position detection: λ1λ2λ3λ4, λ1λ2λ3λ5, λ1λ2λ4λ5, λ1λ3λ4λ5, λ2λ3λ4λ5在图 8a中,曲线1、2、3分别表示以λ1λ2λ3λ4、λ1λ2λ3λ5和λ1λ2λ4λ5为基础的直接极值峰位判定的拉格朗日插值结果,对应波长标定方程分别如式(8)~ 式(10)所示。
\begin{gathered} \lambda_3(x)=1.0094 \times 10^{-8} x^3-1.3983 \times \\ 10^{-5} x^2+0.17121 x+384.4636 \end{gathered} (8) \begin{gathered} \lambda_4(x)=8.7616 \times 10^{-9} x^3-1.2128 \times \\ 10^{-5} x^2+0.17061 x+384.5106 \end{gathered} (9) \begin{gathered} \lambda_5(x)=-9.2794 \times 10^{-9} x^3+1.6395 \times \\ 10^{-5} x^2+0.16109 x+385.2700 \end{gathered} (10) 在图 8b中,曲线1、2分别表示以λ1λ3λ4λ5和λ2λ3λ4λ5为基础的直接极值峰位判定的拉格朗日插值结果,对应波长标定方程分别如式(11)和式(12)所示。
\begin{gathered} \lambda_6(x)=-7.7035 \times 10^{-8} x^3+1.8023 \times \\ 10^{-4} x^2+0.053029 x+395.9236 \end{gathered} (11) \begin{gathered} \lambda_7(x)=-9.6204 \times 10^{-8} x^3+2.4283 \times \\ 10^{-4} x^2-0.014912 x+420.4153 \end{gathered} (12) 在图 8c中,曲线1,2,3,4,5分别表示以λ1λ2λ3λ4,λ1λ2λ3λ5,λ1λ2λ4λ5,λ1λ3λ4λ5,λ2λ3λ4λ5为基础的高斯拟合峰位判定的拉格朗日插值结果,对应波长标定方程分别如式(13)~式(17)所示。
\begin{gathered} \lambda_8(x)=7.7842 \times 10^{-9} x^3-1.0914 \times \\ 10^{-5} x^2+0.17068 x+384.3825 \end{gathered} (13) \begin{gathered} \lambda_9(x)=7.7913 \times 10^{-9} x^3-1.0924 \times \\ 10^{-5} x^2+0.17068 x+384.3823 \end{gathered} (14) \begin{gathered} \lambda_{10}(x)=7.8969 \times 10^{-9} x^3-1.1091 \times \\ 10^{-5} x^2+0.17074 x+384.3778 \end{gathered} (15) \begin{gathered} \lambda_{11}(x)=8.2886 \times 10^{-9} x^3-1.2039 \times \\ 10^{-5} x^2+0.17136 x+384.3159 \end{gathered} (16) \begin{gathered} \lambda_{12}(x)=8.3994 \times 10^{-9} x^3-1.2401 \times \\ 10^{-5} x^2+0.17176 x+384.1745 \end{gathered} (17) 根据光栅色散方程,在一定程度上波长和CCD像素位置的关系可近似为线性关系。由图 8可知,对于直接峰位判定:以λ1λ3λ4λ5为基准的组合在像元位置为3097时,波长的拟合值开始变为负值,以λ2λ3λ4λ5为基准的组合在像元位置为2968时,波长的拟合值开始变为负值,以λ1λ2λ4λ5基准的组合在波长从650 nm开始,曲线的非线性特征增加,出现了拟合值明显偏离真实值的情况;对于高斯拟合峰位判定:从插值曲线难以判断最优波长标定方程。因此通过对比不同残差对所有波长组合进行评估。表 4所示为直接极值定位拉格朗日插值和高斯拟合定位拉格朗日插值残差数据。
表 4 拉格朗日插值法残差分布范围Table 4. Lagrange polynomial residual distribution rangeλ1λ2λ3λ4 λ1λ2λ3λ5 λ1λ2λ4λ5 λ1λ3λ4λ5 λ2λ3λ4λ5 residual of direct peak position detection/nm ±3.41×10-12 ±2.84×10-12 ±1.69393×10-11 ±2.98×10-11 ±7.59×10-11 residual of Gaussian fitting peak position detection/nm ±2.27×10-12 ±6.82×10-13 ±1.09×10-11 ±8.21×10-11 ±1.64×10-10 由表 4可知,采用拉格朗日插值法,残差最小的是以λ1λ2λ3λ5为基准的高斯拟合方法,波长标定残差分布在±6.82×10-13nm范围内,经计算其残差标准差为3.2747×10-13nm。因此采用λ1λ2λ3λ5组合的高斯拟合定位作为波长标定方程。对其波长标定不确定度进行评估:在包含因子k=1时,波长标定不确定度为u≈3.2747×10-13nm,波长标定可靠度水平为68%;在包含因子k=2时,波长标定不确定度为u≈2×3.2747×10-13nm=6.549410-13nm,波长标定可靠度水平为95%。利用拉格朗日插值法最终确定的波长标定方程为:
\begin{gathered} \lambda(x)=\lambda_9(x)=7.7913 \times 10^{-9} x^3- \\ 1.0924 \times 10^{-5} x^2+0.17068 x+384.3823 \end{gathered} (18) 通过对最小二乘法和拉格朗日插值法得到的拟合曲线及残差特性分析可知,拉格朗日插值法的残差较最小二乘法更小,同时在380 nm~980 nm波长范围内拟合曲线均近似为线性。根据光栅色散原理,波长与像素位置存在一定的线性特征。因此确定采用高斯拟合的以λ1λ2λ3λ5为基准的格朗日插值结果作为波长标定方程,最终确定的波长标定方程如式(18)所示。
3.3 波长标定结果验证
为了验证标定精度,本文中采用多种激光对其它波长进行实验验证。通过将实测波长与标准波长进行对比,从而验证波长标定精度。表 5所示为不同波长的测试结果。
表 5 波长测试结果Table 5. Result of wavelength teststandard wavelength/nm measured wavelength/nm error/nm 460.00 460.11 0.11 532.00 531.96 -0.04 650.00 650.16 0.16 通过对表 5的数据分析可知,采用不同激光光源进对波长标定精度进行验证,实测值与标准值偏差分布在±0.2 nm范围内。
4. 结论
针对可见光光谱辐射计在标定时存在峰值偏移、较弱特征谱误判及人工谱线识别等问题,提出了一种改进的自适应阈值波长自动标定方法。将LAMOST动态检测思想应用到光谱辐射计波长标定中,使用标准灯的标准差作为谱线检测过程中的阈值,并且该阈值随着迭代过程动态调整,有效地避免了谱线检测过程中噪声被误认为特征谱的情况。采用差分法代替原有的谱线识别方法,避免了实际测量中因各种噪声导致的谱线强度与理论强度差异过大而出现的谱线识别错误。此外,对极值峰位检测的结果进行高斯拟合,确定了特征波长更加精确的像元位置;对比最小二乘法和拉格朗日插值法确定了波长和像元的最佳函数关系;采用激光对波长标定精度进行验证,结果表明,波长标定精度优于0.2 nm。相比于传统的光谱辐射计,波长标定精度得到了显著的提高,证明该方法能够有效提升波长标定精度,从而可为其它光谱类仪器的波长标定提供参考和借鉴。
-
图 8 拉格朗日多项式插值结果 a—直接极值峰位判定:λ1λ2λ3λ4,λ1λ2λ3λ5,λ1λ2λ4λ5 b—直接极值峰位判定:λ1λ3λ4λ5,λ2λ3λ4λ5 c—高斯拟合峰位判定:λ1λ2λ3λ4,λ1λ2λ3λ5,λ1λ2λ4λ5,λ1λ3λ4λ5,λ2λ3λ4λ5
Figure 8. Results of Lagrange polynomial interpolation a—direct peak position detection: λ1λ2λ3λ4, λ1λ2λ3λ5, λ1λ2λ4λ5 b—direct peak position detection: λ1λ3λ4λ5, λ2λ3λ4λ5 c—Gaussian fitting peak position detection: λ1λ2λ3λ4, λ1λ2λ3λ5, λ1λ2λ4λ5, λ1λ3λ4λ5, λ2λ3λ4λ5
表 1 各器件具体参数
Table 1 Specific parameters of each device
item parameters mercury lamp type:LHM254 probe(camera lens) focal length:50 mm collimating mirror focusing mirror radius:300 mm focal length:150 mm CCD 8 μm×200 μm, number of pixels:3648 grating lines:300 lp/mm size:50 mm×50 mm blaze wavelength:500 nm slit 0.1 mm 表 2 各特征波及两种峰位判断方法对应的峰值位置
Table 2 Characteristic wavelength and peak positions for different methods
serial number characteristic wavelength/nm pixel position Gaussian position 1 404.6565 119 119.6208 2 435.8335 306 306.1324 3 546.0750 967 965.9072 4 576.9610 1143 1143.7210 5 579.0670 1156 1155.6497 表 3 最小二乘法残差分布及标准差
Table 3 Residual distribution and mean squared error for the least squares method
method residual/nm mean squared error/nm direct peak position detection ±0.1097 0.06642 Gaussian fitting peak position detection ±5.86×10-4 3.5578×10-4 表 4 拉格朗日插值法残差分布范围
Table 4 Lagrange polynomial residual distribution range
λ1λ2λ3λ4 λ1λ2λ3λ5 λ1λ2λ4λ5 λ1λ3λ4λ5 λ2λ3λ4λ5 residual of direct peak position detection/nm ±3.41×10-12 ±2.84×10-12 ±1.69393×10-11 ±2.98×10-11 ±7.59×10-11 residual of Gaussian fitting peak position detection/nm ±2.27×10-12 ±6.82×10-13 ±1.09×10-11 ±8.21×10-11 ±1.64×10-10 表 5 波长测试结果
Table 5 Result of wavelength test
standard wavelength/nm measured wavelength/nm error/nm 460.00 460.11 0.11 532.00 531.96 -0.04 650.00 650.16 0.16 -
[1] 刘丽莹, 郑峰, 张国玉, 等. 基于精密太阳光谱辐射计的气象辐射观测[J]. 光谱学与光谱分析, 2018, 38(12): 3663-3672. LIU L Y, ZHENG F, ZHANG G Y, et al. Meteorological radiation observation based on precision solar spectral radiometer[J]. Spectroscopy and Spectral Analysis, 2018, 38(12): 3663-3672(in Chinese).
[2] 王智平, 吴统邦, 李周, 等. 一种通用的红外辐射特性测量技术[J]. 红外, 2020, 41(8): 29-35. WANG Zh P, WU T B, LI Zh, et al. A universal measurement technology for infrared radiation characteristics[J]. Infrared, 2020, 41(8): 29-35(in Chinese).
[3] 吴志峰, 代彩红, 赵伟强, 等. 基于可调谐激光的光谱辐射照度响应度定标[J]. 光谱学与光谱分析, 2021, 41(3): 853-857. WU Zh F, DAI C H, ZHAO W Q, et al. Spectral irradiance responsivity calibration based on tunable laser[J]. Spectroscopy and Spectral Analysis, 2021, 41(3): 853-857(in Chinese).
[4] 阮宁娟, 苏云. 国外紫外空间探测器发展综述[J]. 航天返回与遥感, 2008, 29(3): 71-78. RUAN N J, SU Y. A review of the development of ultraviolet space probe abroad[J]. Spacecraft Recovery & Remote Sensing, 2008, 29(3): 71-78(in Chinese).
[5] REDONDAS A, NEVAS S, BERJÓN A, et al. Wavelength calibration of Brewer spectrophotometer using a tunable pulsed laser and implications to the Brewer ozone retrieval[J]. Atmospheric Measurement Techniques, 2018, 11(6): 3759-3768. DOI: 10.5194/amt-11-3759-2018
[6] 郑克哲. 光学计量[M]. 北京: 原子能出版社, 2002: 138-145. ZHENG K Zh. Optical metrology[M]. Beijing: Atomic Energy Press, 2002: 138-145(in Chinese).
[7] 李香香, 牛海波, 刘会玲, 等. 直接驱动型光栅单色仪的波长标定[J]. 自动化与仪表, 2022, 37(11): 76-79. LI X X, NIU H B, LIU H L, et al. Wavelength calibration of direct drive grating monochromator[J]. Automation & Instrumentation, 2022, 37(11): 76-79(in Chinese).
[8] 张子辉, 王淑荣, 黄煜, 等. 宽波段单色仪多级谱高精度波长定标[J]. 光谱学与光谱分析, 2012, 32(10): 2870-2874. ZHANG Z H, WANG Sh R, HUANG Y, et al. High-precision wavelength calibration of wide-band monochromator[J]. Spectroscopy and Spectral Analysis, 2012, 32(10): 2870-2874(in Chinese).
[9] 武传龙, 冯国英, 韩旭, 等. 微型光纤光谱仪的波长定标分析[J]. 激光技术, 2012, 36(5): 682-685. WU Ch L, FENG G Y, HAN X, et al. Wavelength calibration for miniature fiber optical spectrometers[J]. Laser Technology, 2012, 36(5): 682-685(in Chinese).
[10] 董冰, 郑峰, 石晓光, 等. 基于多项式拟合残差法的光纤光谱仪的波长定标方法研究[J]. 长春理工大学学报(自然科学版), 2017, 40(1): 14-18. DONG B, ZHENG F, SHI X G, et al. Wavelength calibration of the fiber optic spectrometer based on the polynomial fitting residual error method[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2017, 40(1): 14-18(in Chinese).
[11] 李新, 张国伟, 寻丽娜, 等. 短波红外平场光谱仪的波长定标[J]. 光学学报, 2008, 28(5): 902-906. LI X, ZHANG G W, XUN L N, et al. Wavelength calibration of shortwave infrared flat spectroradiometer[J]. Acta Optica Sinica, 2008, 28(5): 902-906(in Chinese).
[12] QIN H Q, ZHU J, ZHU Zh Q, et al. Adaptive wavelength calibration algorithm for LAMOST[J]. Publications of the Astronomical Society of Australia, 2010, 27(3): 265-271.
[13] 马艳, 夏果, 黄禅, 等. 一种简单精确的CCD阵列光谱仪波长定标方法[J]. 红外与激光工程, 2018, 47(S1): S117002. MA Y, XIA G, HUANG Ch, et al. A simple and accurate wavelength calibration method for CCD spectrometer[J]. Infrared and Laser Engineering, 2018, 47(S1): S117002.
[14] 骆佳晨. 光纤光谱仪数据处理算法研究及系统设计与实现[D]. 南京: 南京理工大学, 2020: 9-14. LUO J Ch. Research on data processing algorithms and system design and implementation of fiber optic spectrometer[D]. Nanjing: Nanjing University of Science & Technology, 2020: 9-14(in Chinese).
[15] GALBÁN J, de MARCOS S, SANZ I, et al. CCD detectors for molecular absorption spectrophotometry. A theoretical and experimental study on characteristics and performance[J]. The Analyst, 2010, 135(3): 564-569.
[16] ZONIOS G. Noise and stray light characterization of a compact CCD spectrophotometer used in biomedical applications[J]. Applied Optics, 2010, 49(2): 163-169.
[17] DAVENPORT J J, HODGKINSON J, SAFFELL J R, et al. Noise analysis for CCD based ultra-violet and visible spectrometry[J]. Applied Optics, 2015, 54(27): 8135-8144.
[18] 胡广书. 数字信号处理[M]. 第2版. 北京: 清华大学出版社, 2003: 327-351. HU G Sh. Digital signal processing[M]. 2nd ed. Beijing: Tsinghua University Press, 2003: 327-351(in Chinese).
[19] 黄曙江. 入射光斜入射光栅表面的衍射方程[J]. 物理通报, 2004(2): 7-8. HUANG Sh J. Diffraction equation of oblique incident light on grating surface[J]. Physics Bulletin, 2004(2): 7-8(in Chinese).
[20] 李庆扬, 王能超, 易大义. 数值分析[M]. 第4版. 北京: 清华大学出版社, 2008: 21-62. LI Q Y, WANG N Ch, YI D Y. Numerical analysis[M]. 4th ed. Beijing: Tsinghua University Press, 2008: 21-62(in Chinese).
[21] SANSONETTI C J, SALIT M L, READER J. Wavelengths of spectral lines in mercury pencil lamps[J]. Applied Optics, 1996, 35(1): 74-77.
[22] RODRÍGUEZ A A, BRUNO L B, RAPETTI F. Whitney edge elements and the Runge phenomenon[J]. Journal of Computational and Applied Mathematics, 2023, 427(3): 115117.
[23] 刘丽莹. 精密光谱辐射计的定标与特性表征[D]. 长春: 长春理工大学, 2019: 79. LIU L Y. Calibration and characterization of precision spectroradiometer[D]. Changchun: Changchun University of Science and Technology, 2019: 79(in Chinese).




 下载:
下载: