网站地图
-
随着低空开放，直升机的应用范围不断扩大，特别是发生重大自然灾害时执行紧急救援任务，任务地点的不确定性增强，因此保证直升机安全着陆显得尤为重要。相关领域的科研人员也开始关注直升机助降问题，直升机辅助起降技术逐渐形成一个研究的热点[1]。无线紫外光通信作为一种新兴的无线通信方式，其在特殊场景下可实现全天候、复杂环境、高可靠性的保密通信，是直升机助降过程中辅助通信方式的最佳选择。
日盲紫外光波长为200nm~280nm，在大气信道中传输时会被气溶胶粒子散射而改变传输方向实现近直视(approximate-line-of-sight，ALOS)通信，克服了其它无线激光通信只能直视通信的不足，且有背景噪声小和抗干扰能力强等特点[2]。尽管紫外光的大气散射特性能实现近直视通信，但散射作用会引起信号衰落加剧、增大误比特率(bit error rate, BER)，导致通信覆盖范围小、通信质量差等问题。作者[3-4]把紫外光通信系统应用于直升机辅助起降，帮助直升机建立应急通信、备降区域锁定取和飞行引导，并提出了相应的机群间路径恢复算法。XIAO [5]等人针对通信系统中的各种参量提出了相应的计算方法，理论分析结果表明，在强湍流下，通信距离增加会导致闪烁衰减增大。
近几年，很多学者在研究大气湍流对无线光通信的影响，但大多数都侧重于自由空间光通信，并且都基于理论研究和仿真实验。QIANG等人[6]根据折射率结构常数垂直分布特性，计算了湍流强度、高空位置、通信距离等因素对紫外光通信系统的影响，发现采取降低仰角可以降低闪烁指数，增加通信距离。XIAO等人[7]进行了弱湍流对紫外光通信影响的理论研究，在开关键控(on-off keying, OOK)调制方式下分析了通信系统的误比特率性能。ZHANG等人[8]采用gamma-gamma湍流模型仿真信道中的大气湍流，并分析了折射率结构常数对脉冲位置调制方式(pulse position modulation, PPM)的影响，结果表明，折射率结构常数越小，PPM调制的Turbo码性能越好。WANG等人[9]验证了大气湍流对紫外光的衰减作用，中等强度湍流(Cn2=10-14m-2/3)下比无湍流时信噪比(signal-to-noise ratio, SNR)降低20dB，并通过增大接收孔径的方法降低了湍流对通信系统的衰减。WANG[10]根据紫外光通信的特点建立紫外光通信弱湍流下的分集接收模型，并在实验室环境下进行了仿真分析和实验验证，结果表明, 分集接收能提升通信系统误比特率性能。由此可以看出，国内紫外光通信系统相关研究大多为理论分析阶段，且处于实验室环境下，在特殊应用场景下的研究就更鲜有人涉及。
虽然相关学者对紫外光通信进行了很多实验室环境下的探究，在直升机助降应用中，中强湍流对紫外光通信的影响很少有人进行分析研究，且尚未找到一种合适的方法来进行抑制。本文中首先通过紫外光近直视通信系统修正模型分析了强湍流对紫外光通信的影响，然后采用分集接收技术来抑制大气湍流效应，降低了通信系统误比特率，并对比3种合并方式的性能差异，为推动紫外光通信的实际应用提供理论支持。
-
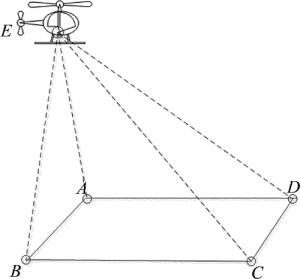
直升机助降模型如图 1所示。直升机备降区域有A, B, C, D 4个定位点，分别放置4个不同波段的紫外发光二极管(light emitting diode, LED)作为发射装置，E为直升机位置。在直升机降落时，日盲紫外光不仅会受到大气的吸收和散射作用，直升机尾翼气流引起的湍流效应也使得接收到的紫外光信号闪烁指数变大，通信系统误比特率增大[11]。在紫外光引导直升机助降过程中，直升机先到达备降区域，接收装置悬挂在直升机底部，接收地面4个定位点发来的位置信息。飞行员根据得到的地面信息，调整机身的降落姿态到达最佳着陆点，实现安全快速降落目的。
Figure 1. Model of helicopter assisted landing
-
直升机降落过程通信系统收发端相对位置是动态变化的，并且水平距离和高度差会一直存在，直至安全降落。因其收发端的相对位置是时变的，紫外光直视和非直视通信传统模型无法很好地拟合该应用场景，故定义添加了水平距离和垂直高度变量后的修正模型为紫外光近直视通信模型。紫外光通信应用在直升机助降过程中，根据相对位置的不同可分为3种：水平通信方式、垂直通信方式和斜程通信方式。其中水平通信和垂直通信可分别看作是斜程通信垂直高度为0和水平距离为0时的特殊形式，在此只选取斜程通信进行研究, 该通信方式如图 2所示。当以T作为发送端、R为接收端时，从图 2中能看出, 收发端之间高度差为h，相对水平距离为r，此时为斜程通信。若以地平面作为参考面，定义发散角为φ1，接收视场角为φ2，发送仰角为θ1，接收仰角为θ2，θ1′为斜程通信方式中的发送仰角，θ2′为斜程通信方式中接收仰角，有效散射体为V，发送端到接收端的直线距离表示为r0，则发送端到有效散射体的距离为r1，有效散射体到接收端的距离为r2。设接收端R与发送端T相对水平线和相对垂直高度线构成直角三角形[12]，两直角边分别为r和h，根据勾股定理可得收发端的直线距离r0，即${r_0} = \sqrt {{r^2} + {h^2}} $。
Figure 2. Model of UV slope communication
-
对于局部均匀的大气湍流，其强弱通常用结构常数Cn2来表示。一般水平路径上，高度和风速基本是已知的，所以Cn2为常数；直升机助降的斜程通信系统中，高度和风速都是不均匀的，所以Cn2也不是恒定值，其变化受海拔、气温、风速、气压等有关。常用的Cn2模型有很多，国际电联给出一种新的垂直分布模型[13]：
$ \begin{array}{*{20}{c}} {C_n^2\left( h \right) = 8.148 \times {{10}^{ - 56}}{v_{{\rm{RMS}}}}^2{h^2}\exp \left( { - \frac{h}{{100}}} \right) + }\\ {2.7 \times {{10}^{ - 16}}\exp \left( { - \frac{h}{{1500}}} \right) + C_0^2\exp \left( { - \frac{h}{{100}}} \right)} \end{array} $
(1) 式中，C02是近地面的大气结构常数，vRMS是垂直路径上的均方根风速，且${v_{{\rm{RMS}}}} = \sqrt {{v_g}^2 + 30.69{v_g} + 348.91} $。${v_{\rm{g}}} = 3 + 17{\rm{exp}}\left[{- {{\left( {\frac{h}{{1000}} - 12.5} \right)}^2}/16} \right]$, h表示海拔高度(m)。近地面处Cn2的标准范围为10-12m－2/3(强湍流)~10－18m－2/3(弱湍流)。大气对流强度是影响大气湍流强度的主要因素，海拔高度h不断变大，Cn2随之减小。此外，在直升机降落过程中，紫外光近直视通信信道中的Cn2是随着海拔高度、温度和风速等因素不断变化的，直升机尾流风速也能使Cn2变大，强湍流导致光信号的闪烁指数变大，误比特率上升，降低通信系统稳定性，严重时可能会使通信中断。
-
大气湍流的相关论述中多是点对点的直视通信，其信号强度分布模型也是在直视通信链路场景下进行探究，针对自由空间光直视通信的系统模型，因其信号强度分布模型不同，在近直视通信系统中无法直接使用。本文中将紫外光近直视通信模型当作是两段或多段点对点直视通信的组合模型，通过建立一个联合概率分布函数来计算接收端的信号强度分布[14]。一般认为，Cn2=10－18m－2/3时为弱湍流，服从对数正态分布；在中强湍流下，更多采用gamma-gamma模型，从弱湍流到强湍流都能很好地拟合接收光强的分布特性，其概率密度函数可表示为[15]：
$ f{\left( I \right)_{{\rm{GG}}}} = \frac{{2{{\left( {\alpha \beta } \right)}^{\frac{{\alpha + \beta }}{2}}}}}{{{\rm{\Gamma }}\left( \alpha \right){\rm{\Gamma }}\left( \beta \right)}}{I^{\frac{{\alpha + \beta }}{2} - 1}}{{\rm{K}}_{\alpha ,\beta }}\left( {2\sqrt {\alpha \beta I} } \right) $
(2) 式中，Γ()为gamma函数，K()为修正的贝塞尔函数，α表示光强闪烁指数强度大小的外尺度，β表示光强闪烁指数强度大小的内尺度，I为接收端接收到的信号强度。当β=1时，双gamma分布模型转化为K分布模型，其概率密度函数可表示为：
$ f{\left( I \right)_{\rm{K}}} = \frac{{2{\alpha ^{\frac{{\alpha + 1}}{2}}}}}{{{\rm{\Gamma }}\left( \alpha \right)}}{I^{\frac{{\alpha - 1}}{2}}}{{\rm{K}}_{\alpha ,1}}\left( {2\sqrt {\alpha I} } \right) $
(3) 式中，α是信道参量，其与离散散射体的有效数目相关，α随湍流强度变化而变化，湍流强度越强其值越小。则K分布下的光强闪烁指数为：
$ \sigma _I^2 = \frac{{E\left( {{I^2}} \right) - {E^2}\left( I \right)}}{{{E^2}\left( I \right)}} = \frac{{\alpha + 2}}{\alpha } $
(4) 式中，E为接收信号强度。由(4)式可以看出，σI2随信道参量α的变化而变化，湍流强度越大闪烁指数σI2越大。
紫外光近直视通信链路模型如图 2所示。在近直视通信链路模型中，设Ir1是从发射端到达散射体的平均信号强度，Ir2是接收端的平均信号强度。从发射端到达有效散射体的信号强度概率密度函数为：
$ f{\left( {{I_{{r_1}}}} \right)_{\rm{K}}} = \frac{{2{\alpha _{{r_1}}}^{\frac{{\left( {{a_{{r_1}}} - 1} \right)}}{2}}}}{{{\rm{\Gamma }}\left( {{\alpha _{{r_1}}}} \right)}}{I_{{r_1}}}^{\frac{{\left( {{a_{{r_1}}} - 1} \right)}}{2}}{{\rm{K}}_{{\alpha _{{r_1}}},1}}\left( {2\sqrt {{\alpha _{{r_1}}}{I_{{r_1}}}} } \right) $
(5) 式中，αr1为r1路径的光强闪烁。从有效散射体到接收端的信号强度的条件概率密度函数为：
$ f{\left( {{I_{{r_2}}}\left| {{I_{{r_1}}}} \right.} \right)_{\rm{K}}} = \frac{{2{\alpha _{{r_2}}}^{\frac{{{a_{{r_2}}} + 1}}{2}}}}{{{\rm{\Gamma }}\left( {{\alpha _{{r_2}}}} \right)}}{I_{{r_2}}}^{\frac{{{a_{{r_2}}} - 1}}{2}}{{\rm{K}}_{{\alpha _{{r_2}}},1}}\left( {2\sqrt {{\alpha _{{r_2}}}{I_{{r_2}}}} } \right) $
(6) 式中，αr2为r2路径的光强闪烁。综合(5)式和(6)式，得到紫外光近直视通信系统中接收端信号强度的边缘分布概率密度函数为[16]：
$ f\left( {{I_{{r_2}}}} \right) = \int {f\left( {{I_{{r_2}}}\left| {{I_{{r_1}}}} \right.} \right)f\left( {{I_{{r_1}}}} \right){\rm{d}}\left( {{I_{{r_1}}}} \right)} $
(7) -
根据TAYLOR的冻结假设，与光传播的速度相比，大气湍流的运动是极其缓慢的，因此湍流信道是一种准静态的大气信道[17]。假设信道只存在高斯噪声，则采用OOK调制时的通信系统模型可表示为[15]:
$ y = x\eta I + v\left( I \right) $
(8) 式中，y为接收端得到的信号强度；x表示开关键控调制信号(0, 1)，η为光电转换效率；Ι为接收器接收到的光强；v(I)为加性高斯白噪声。定义系统信噪比γ为：
$ \gamma = \frac{{{{\left( {\eta I} \right)}^2}}}{{2\sigma _v^2}} $
(9) 式中，σv2为零均值加性高斯白噪声v(I)的方差，且$\sigma _v^2 = \frac{{{N_0}}}{2}$，N0是均值为零的噪声功率。
无线紫外光通信系统调制方式采用OOK，其误比特率Pe表示为[18]：
$ {P_{\rm{e}}} = p\left( 0 \right)p\left( {e\left| 0 \right.} \right) + p\left( 1 \right)p\left( {e\left| 1 \right.} \right) $
(10) 式中，p(0)是系统发送0的概率，p(1)是系统发送1的概率；p(e|0)为发送0时接收端接收到信号的条件概率，p(e|1)为发送1时接收端收到信号的条件概率。系统发送1和0的概率是相同的，即p(0)=p(1)=$\frac{1}{2}$，且$p\left( {e\left| 0 \right.} \right){\rm{ = }}p\left( {e\left| 1 \right.} \right) = Q\left( {\frac{{\eta \mathit{ I}}}{{\sqrt {2{N_0}} }}} \right)$。则OOK调制方式下的系统平均误比特率为：
$ {P_{\rm{e}}} = \int_0^\infty {f\left( I \right)Q\left( {\frac{{\eta I}}{{\sqrt {2{N_0}} }}} \right){\rm{d}}I} $
(11) 已知关系式erfc(x)=2Q($\sqrt {2x} $)，erfc()为误差函数。将概率密度函数f(Ir2)和Q函数都带入(11)式, 可得K分布信道模型中的平均误比特率，公式为：
$ {P_{{\rm{e,K}}}} = \frac{1}{2}\int_0^\infty {f\left( {{I_{{r_2}}}} \right){\rm{erfc}}\left( {\frac{{\eta {I_{{r_2}}}}}{{\sqrt {2{N_0}} }}} \right){\rm{d}}{I_{{r_2}}}} $
(12) -
假设输入支路有N条，令第i条支路接收信号为xi(t)(i=1, 2, …, N)，第i条接收支路的加权系数为ωi。则分集合并后的输出为：
$ \begin{array}{*{20}{c}} {y\left( t \right) = {\omega _1}{x_1}\left( t \right) + {\omega _2}{x_2}\left( t \right) + \cdots + }\\ {{\omega _N}{x_N}\left( t \right) = \sum\limits_{i = 1}^N {{\omega _i}{x_i}\left( t \right)} } \end{array} $
(13) 式中，t为时间。接收端通过某种加权方式将携带相同信息的多路相互独立的信号进行合并，达到提高通信系统信号信噪比的目的，这就是合并技术，合并方式的分类是由加权系数ωi所决定的。常用的合并方式有：最大比合并(maximum ratio combination, MRC)、等增益合并(equal gain merging, EGC)和选择性合并(selective merging, SC)。
-
最大比合并的原理是3种合并方式中最复杂的，根据各支路的加权系数与该支路的信噪比成正比的特点，每条支路的信号都与该支路的加权系数相乘，然后各路相加，信噪比大的支路信号占据合并输出信号的比例大，对系统信噪比性能的提升明显。合并输出的信噪比为[15]：
$ {\gamma _{{\rm{MRC}}}} = {\left( {\frac{\eta }{{\sqrt {2N} }}} \right)^2}\sum\limits_{i = 1}^N {\frac{{I_i^2}}{{\sigma _v^2}}} = \sum\limits_{i = 1}^N {{\gamma _i}} $
(14) 式中, 某一条信噪比可表示为${\gamma _i} = {(\eta {\mathit{I}_i}\sqrt {2N{\sigma _v}^2} )^2}$，MRC合并的误比特率公式为：
$ {P_{{\rm{e,MRC}}}} = \int_0^\infty {f\left( {{I_{{r_2}}}} \right)Q\left( {\frac{\eta }{{\sqrt {2N{N_0}} }}\sqrt {\sum\limits_{i = 1}^N {{I_{{r_2},i}}^2} } } \right){\rm{d}}{I_{{r_2}}}} $
(15) 式中，Ir2, i为第i路近直视链路的接收信号强度。利用$Q\left( x \right) \approx \frac{1}{{12}}{\rm{exp}}\left( { - \frac{{{x^2}}}{2}} \right) + \frac{1}{4}{\rm{exp}}\left( { - \frac{{2{x^2}}}{3}} \right)$对上式积分进行化简可得：
$ \begin{array}{*{20}{c}} {{P_{\rm{e}}} \approx \frac{1}{{12}}\prod\limits_{i = 1}^N {\int_0^\infty {f\left( {{I_{{r_2},i}}} \right)\exp \left( { - \frac{{{\eta ^2}}}{{4N{N_0}}}{I_{{r_2},i}}^2} \right){\rm{d}}{I_{{r_2},i}}} } + }\\ {\frac{1}{4}\prod\limits_{i = 1}^N {\int_0^\infty {f\left( {{I_{{r_2},i}}} \right)\exp \left( { - \frac{{{\eta ^2}}}{{3N{N_0}}}{I_{{r_2},i}}^2} \right){\rm{d}}{I_{{r_2},i}}} } } \end{array} $
(16) -
等增益合并可以看作是最大比合并的一种特殊情况，它的各支路信号的加权系数都相等，且都为定值，类比最大比合并输出信噪比公式，则EGC合并输出的信噪比可表示为：
$ {\gamma _{{\rm{EGC}}}} = {\left( {\frac{\eta }{{\sqrt {2N\sigma _v^2} }}} \right)^2}\sum\limits_{i = 1}^N {{I_i}^2} $
(17) 把信噪比(17)式带入误比特率(12)式，并进行化简，可以得出等增益合并方式的误比特率公式为：
$ {P_{{\rm{e,EGC}}}} = \int_0^\infty {f\left( {{I_{{r_2}}}} \right)Q\left( {\frac{\eta }{{N\sqrt {2{N_0}} }}\sum\limits_{i = 1}^N {{I_{{r_2},i}}} } \right){\rm{d}}{I_{{r_2}}}} $
(18) 利用$Q\left( x \right) \approx \frac{1}{{12}}{\rm{exp}}\left( { - \frac{{{x^2}}}{2}} \right) + \frac{1}{4}{\rm{exp}}\left( { - \frac{{2{x^2}}}{3}} \right)$对上式积分进行化简可得：
$ \begin{array}{*{20}{c}} {{P_{{\rm{e,EGC}}}} \approx \frac{1}{{12}}{{\left[ {\int_0^\infty {f\left( {{I_{{r_2}}}} \right)\exp \left( { - \frac{{{\eta ^2}{I_{{r_2}}}^2}}{{4N{N_0}}}} \right){\rm{d}}{I_{{r_2}}}} } \right]}^N} + }\\ {\frac{1}{4}{{\left[ {\int_0^\infty {f\left( {{I_{{r_2}}}} \right)\exp \left( { - \frac{{{\eta ^2}{I_{{r_2}}}^2}}{{3N{N_0}}}} \right){\rm{d}}{I_{{r_2}}}} } \right]}^N}} \end{array} $
(19) -
选择合并是上述3种合并技术中最简单的1种，它的原理是监测所有支路信号的信噪比，只需要从N条支路中选取1条支路作为输出，与MRC和EGC相比合并算法复杂度降低。但是该合并方式牺牲了合并所带来的增益，并且需要实时监测各支路，选出信噪比最大的支路作为输出。其输出信号为：
$ {I_{{\rm{SC}}}} = \max \left\{ {{I_1},{I_2},{I_3}, \cdots ,{I_N}} \right\} $
(20) 在所有加权系数中，只有信噪比最大的一路为1，其余的都为0，即:
$ {\omega _i} = \left\{ \begin{array}{l} 1,\left( {{\gamma _{{\rm{SC}}}} = \max \left\{ {{I_1},{I_2},{I_3}, \cdots ,{I_N}} \right\}} \right)\\ 0,\left( {{\rm{else}}} \right) \end{array} \right. $
(21) 式中，γSC为选择合并的信噪比。gamma-gamma湍流模型下其概率密度函数为：
$ {f_{{\rm{SC}}}}\left( {{I_{{r_2}}}} \right) = \frac{{{\rm{d}}{F_{{\rm{SC}}}}\left( {{I_{{r_2}}}} \right)}}{{{\rm{d}}{I_{{r_2}}}}} = N{F_{{\rm{SC}}}}{\left( {{I_{{r_2}}}} \right)^{N - 1}}f\left( {{I_{{r_2}}}} \right) $
(22) 式中，FSC(Ir2)为选择合并的N条支路输出的分布函数，选择合并的平均误比特率公式可以表示为：
$ {P_{{\rm{e,SC}}}} = \int_0^\infty {{f_{{\rm{SC}}}}\left( {{I_{{r_2}}}} \right)Q\left( {\frac{{\eta {I_{{r_2},{\rm{SC}}}}}}{{2\sqrt {N{N_0}} }}} \right){\rm{d}}{I_{{r_2},{\rm{SC}}}}} $
(23) 式中，Ir2, SC为近直视通信选择合并时的接收信号强度。把概率密度函数f(Ir2)带入(23)式可得：
$ \begin{array}{*{20}{c}} {{P_{{\rm{e,SC}}}} = \int_0^\infty {N{F_{{\rm{SC}}}}{{\left( {{I_{{r_2}}}} \right)}^{N - 1}}f\left( {{I_{{r_2}}}} \right)} \times }\\ {Q\left( {\frac{{\eta {I_{{r_2},{\rm{SC}}}}}}{{2\sqrt {N{N_0}} }}} \right){\rm{d}}{I_{{r_2},{\rm{SC}}}}} \end{array} $
(24) -
首先仿真分析风速和距离对湍流强度的影响。根据第3节中推导出的MRC, EGC和SC 3种分集合并方法的误比特率公式，仿真分析湍流效应对通信系统误比特率性能的影响，以及这3种合并方法在直升机助降紫外光近直视通信系统中对强湍流效应的抑制作用，并对比了3种不同合并方式之间的性能差异。部分仿真参量的选取如表 1所示。通信速率设定为100kbit/s。
Table 1. Parameters of the system simulation
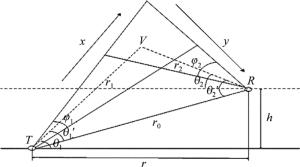
parameter value receiving aperture area Ar 1.77cm2 attenuation coefficient Ke 1.961×10-3 scattering coefficient Ks 0.759×10-3 photoelectric response Pr 48mA/W 根据(1)式可知，大气折射率结构常数Cn2增大，对应的湍流强度也会增强。图 3为大气折射率结构常数垂直分布仿真。从图中可以看出，距离地面越近，大气湍流越强，仿真结果与公式分析基本相符。因此在直升机降落过程中，湍流效应对通信系统的影响是不可忽略的，通过抑制湍流效应能有效改善通信系统的性能。
Figure 3. Distribution diagram of atmospheric refractive index structure constant
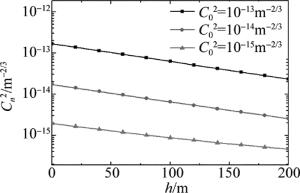
当水平ALOS通信时，以Cn2表征湍流特性，而在垂直ALOS通信时，由于Cn2是随高度变化的，因此采用C02表征湍流特性。图 4a为不同湍流强度下水平近直视通信的接收端信号强度概率密度函数分布(归一化信号强度)。收发仰角均为60°，水平距离r=100m，湍流强度从10-16m-2/3~10-13m-2/3, 信号强度发散，并剧烈衰减，当湍流强度增强到10-13m-2/3时，信号能量衰减到几乎无法实现通信的程度。由此可以看出, 湍流效应对无线紫外光水平ALOS通信接收光强的概率密度分布影响较大。
Figure 4. Effect of horizontal distance and vertical height on UV communication
图 4b为不同湍流强度下垂直近直视通信的信号强度概率密度函数分布(归一化信号强度)。在垂直ALOS通信时，Cn2是不定的，所以选取地面大气折射率结构常数表征湍流强度，收发仰角均为60°，水平距离h=100m，湍流强度从10-16m-2/3~10-13m-2/3，信号强度发散，在强湍流为10-15m-2/3和10-14m-2/3时，垂直通信和水平通信的概率密度相近，信号强度衰减也很剧烈，当湍流强度增强到10-13m-2/3时，信号能量发散严重。由此可以看出，湍流效应对无线紫外光垂直ALOS通信接收光强的概率密度分布影响较大。
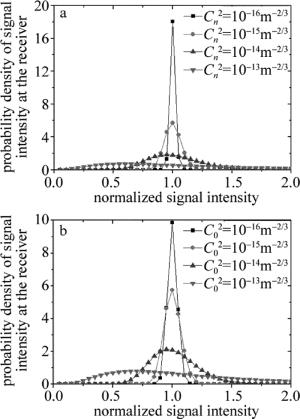
图 5仿真了紫外光近直视通信系统闪烁指数σI2对误比特率的影响。由第1.4节中可知, 湍流强度与闪烁指数σI2的关系，定义湍流强度越强，闪烁指数σI2越大；一般认为在无线光通信中当闪烁指数σI2>1时大气湍流为强湍流，所以分别选取了σI2为1.02，2，4，6，8这5种闪烁指数所对应的湍流强度进行分析。随着闪烁指数σI2增强，通信系统误比特率逐渐增大，说明湍流强度越大，通信系统的误比特率性能越差。从图中还可以看出, 湍流影响下的信噪比在60dB时, 误比特率才达到通信系统的最低要求10-3，由此可见，在直升机助降紫外光近直视通信系统中，有效抑制大气湍流效应带来的影响很有必要。
Figure 5. Influence of scintillation index on BER
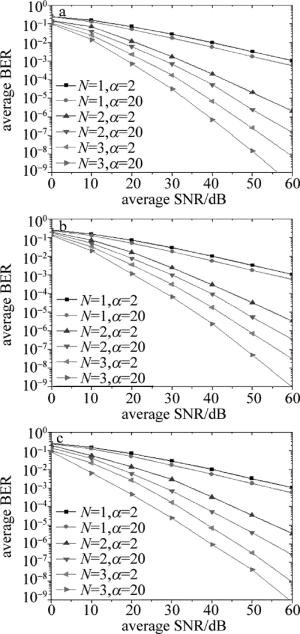
图 6a是对MRC合并方式在不同接收天线和信道参量下系统误比特率性能仿真图。由图可知，当N=1时, 即为未分集接收，湍流效应越强，系统性能越差，未采用分集接收时误比特率要达到10-3，信噪比需要58dB，而N为2和3时, 分别只需要36dB，25dB，这说明MRC合并方式能明显提升系统性能。当N为1~3时，MRC合并在两种湍流强度下系统性能的差距也逐渐变大，说明MRC合并技术可以有效抑制湍流效应带来的影响，接收天线越多对湍流的抑制作用就越明显。
Figure 6. Performance simulation of three kinds of combining methods
图 6b是EGC合并方式下接收天线和信道参量系统误比特率性能仿真图。在信道参量相同情况下, 未采用分集接收时误比特率要达到10-3，信噪比需要58dB，而N为2和3时, 分别只需要40dB，27dB，说明EGC合并方式能明显提升系统性能。当N为1~3时，两种湍流强度下EGC合并方式对性能的提升效果也不同，接收天线越多对湍流的抑制作用就越明显。
图 6c是对SC合并方式在不同接收天线和信道参量下系统误比特率性能仿真图。由图可知，湍流强度变大时，系统性能变差，未采用分集接收时误比特率要达到10-3，信噪比需要58dB，而N为2和3时, 分别只需要42dB，29dB，说明SC合并方式能明显提升系统性能。不同湍流强度下，SC合并对系统性能的提升程度不同，说明SC合并技术能有效抑制湍流效应带来的影响，接收天线越多, 对湍流的抑制作用就越明显。
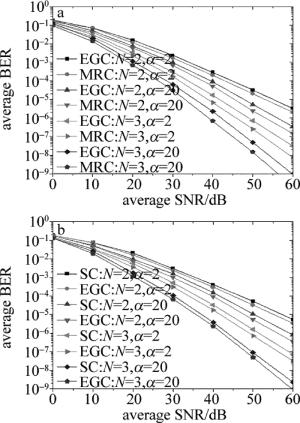
图 7a为MRC合并方式和EGC合并方式的误比特率性能对比仿真图。从图中可以看出, 虽然MRC合并方式和EGC合并方式都能提升系统误比特率性能，但MRC合并方式的效果要比EGC合并方式略好一点，性能差距约为4dB，不过随着接收天线数的增加, 这种差距会扩大。同样的接收天线数时，MRC合并方式也比EGC合并方式对湍流的抑制作用稍强，不过两者对系统的误比特率性能提升差距很小。
Figure 7. Performance comparison of three kinds of combining methods
图 7b为EGC合并方式和SC合并方式的误比特率性能对比仿真图。可以看出, SC合并方式和EGC合并方式都能在一定程度上提升系统性能，抑制湍流效应。在相同接收天线和信达参量时，EGC合并方式比SC合并方式都对系统性能的提升大2dB左右，并且随着接收天线数的增加，EGC合并方式和SC合并方式对系统性能的提升差距逐渐变大。
-
直升机助降场景中紫外光近直视通信系统性能会受到大气湍流的影响，推导出接收光强概率密度函数公式，建立强湍流信道下紫外光近直视通信修正模型。随着斜程通信相对位置增大，通信系统的信号强度概率密度函数分布分散，能量衰减严重，大气湍流效应严重影响该通信方式下的系统误比特率性能。通过给出的近直视通信系统在3种分集合并方式的误比特率公式得出：MRC, EGC, SC这3种合并方式都能对大气湍流效应有一定的抑制作用，随着分集天线的增加3种合并方式的对系统性能的提升也越来越大。说明分集接收技术能有效抑制强湍流效应，提升通信系统的稳定性和抗衰落性能，成为无线紫外光通信应用于直升机助降的有力保障。考虑到MRC合并方式需要计算接收信号的信噪比，计算复杂度较高，EGC和SC相对较为简单，但EGC性能相对于SC要高2dB左右，因此, 在实际应用中要根据具体需求做出合理选择。
直升机助降中紫外光近直视通信分集接收技术
Diversity receiving technology of ultraviolet approximate-line-of-sight communication in helicopter assisted landing
-
摘要: 为了有效抑制直升机降落过程中尾流造成的强湍流效应，采用分集接收技术来进行抑制。根据无线紫外光斜程通信和近直视通信的特性，给出接收信号强度的边缘分布概率密度函数，建立了基于gamma-gamma分布的紫外光近直视通信系统修正模型，将分集接收技术引入该模型。理论分析了湍流效应对接收光信号强度边缘概率密度分布的影响以及最大比合并（MRC）、等增益合并（EGC）和选择性合并（SC）的误码性能。结果表明，大气湍流强度越强，紫外光近直视通信系统的误比特率性能越差；二分集时，MRC，EGC，SC 3种合并方式信噪比性能分别提升了22dB，18dB，16dB。分集接收技术能有效抑制直升机助降过程中的强湍流效应，提升通信系统的稳定性和抗衰落性能。Abstract: In order to effectively suppress the strong turbulence effect caused by the wake of helicopter during landing, diversity reception technology was used for suppression.According to the characteristics of wireless ultraviolet slant communication and approximate-line-of-sight (ALOS) communication, the probability density function of edge distribution of the received signal strength was given.The correction model of UV ALOS communication system based on gamma-gamma distribution was established.The diversity reception technology was introduced into the model.The influence of turbulence effect on the edge probability density distribution of optical signal intensity was analyzed theoretically.Bit error performances of maximal ratio combining (MRC), equal gain combining (EGC) and selective combining (SC) were analyzed.The results show that, the stronger the turbulence intensity is, the worse the bit error rate performance of UV ALOS system is.With two diversities, the signal-to-noise rates of MRC, EGC and SC have increased 22dB, 18dB and 16dB respectively.The diversity reception technology can effectively suppress the strong turbulence effect in helicopter assisted landing and improve the stability and anti-fading performance of communication system.
-
Figure 4. Effect of horizontal distance and vertical height on UV communication
a—horizontal ALOS communication b—vertical ALOS communication
Figure 7. Performance comparison of three kinds of combining methods
a—comparison of MRC merge and EGC merge performance b—comparison of EGC merge and SC merge performance
Table 1. Parameters of the system simulation
parameter value receiving aperture area Ar 1.77cm2 attenuation coefficient Ke 1.961×10-3 scattering coefficient Ks 0.759×10-3 photoelectric response Pr 48mA/W 
下载: 导出CSV
-
[1] ZHANG H L, YIN H W, JIA H H, et al. Study of effects of obstacle on non-line-of-sight ultraviolet communication links[J]. Optics Express, 2011, 19(22):21216-21226. doi: 10.1364/OE.19.021216 [2] EL-SHIMY M A, HRANILOVIC S. Binary-input non-line-of-sight solar-blind UV channels:Modeling, capacity and coding[J]. Optical Communications and Networking, 2012, 4(12):1008-1017. doi: 10.1364/JOCN.4.001008 [3] ZHAO T F, WU P F, SONG P. Research on the wireless ultraviolet communication technology in helicopter launching and landing guidance[J]. Laser Journal, 2014, 35(10):9-13(in Chinese). [4] ZHAO T F, LENG Y X, WANG Y. Path fast recovery algorithm of inter clusters for UV NLOS communication[J]. Laser Technology, 2017, 41(5):728-733(in Chinese). [5] XIAO H F, ZUO Y, FAN Ch, et al. Non-line-of-sight ultraviolet channel paramaters estimation in turbulence atmosphere[C]//Communications and Photonics Conference(ACP).New York, USA: IEEE, 2012: 1-3. [6] QIANG R X, ZHAO Sh H, WANG X, et al. Influence of high atmosphere turbulence on scintillation in non-line-of-sight ultraviolet channel[J]. Semiconductor Optoelectronics, 2014, 35(4):677-681(in Chinese). [7] XIAO H F. Study on propagation models of ultraviolet communication systems[D]. Beijing: Beijing University of Posts and Telecommunications, 2014: 62-66(in Chinese). [8] ZHANG X H, ZUO Y, ZHAO Y B, et al. Effects of UV communication channel parameters on Turbo code[J]. Study on Optical Communications, 2014, 40(6):73-75(in Chinese). [9] WANG J Y, SONG X M, SONG P, et al. The effect of atmospheric turbulence on wireless ultraviolet communication[J]. Journal of Xi'an Polytechnic University, 2016, 30(3):322-326(in Chinese). [10] WANG X Y. Technology research and system implementation of UV optical communications[D]. Beijing: Beijing University of Posts and Telecommunications, 2014: 16-25(in Chinese). [11] ZHAO T F, WANG X F, LIU Y. Modulation research of helicopter landing using ultraviolet guiding technology in atmospheric turbulence[J]. Laser Technology, 2017, 41(3):411-415(in Chinese). [12] HE H, KE X Zh, ZHAO T F. Research of ALOS ultraviolet single scattering link model with height information[J]. Laser Technology, 2011, 35(4):495-498(in Chinese). [13] MA B K. Study on the related problems of (light)beam propagation in the atmospheric turbulence[D]. Xi'an: Xidian University, 2008: 7-17(in Chinese). [14] ZHAO T F, LIU Y, WANG Y, et al. Performance analysis of ultraviolet communication in helicopter assisted landing[J]. Journal of Xi'an University of Technology, 2016, 32(2):163-168(in Chinese). [15] TSIFTSIS T A, SANDALIDIS H G, KARAGIANNIDIS G K,et al. Optical wireless links with spatial diversity over strong atmospheric turbulence channels[J]. IEEE Transactions on Wireless Communications, 2009, 8(2):951-957. doi: 10.1109/TWC.2009.071318 [16] ZUO Y, XIAO H F, WU J. Effect of atmospheric turbulence on Non-line-of-sight ultraviolet communications[C]//2012 IEEE 23rd International Symposium on Persoal, Indoor and Mobile Radio Communications(PIMRC).New York, USA: IEEE, 2012: 1682-1686. [17] KE X Zh, LIU M. Diversity reception technology over atmospheric turbulence channels in wireless optical communication[J]. Acta Optica Sinica, 2015, 35(1):88-95(in Chinese). [18] NAVIDPOUR S M, UYSAL M, KAVEHRAD M. BER performance of free-space optical MIMO transmission with spatial diversity[J].IEEE Transactions on Wireless Communications, 2007, 6(8):2813-2819. doi: 10.1109/TWC.2007.06109 -
点击查看大图
图(7) / 表(1)
计量
- 文章访问数: 8229
- HTML全文浏览量: 6090
- PDF下载量: 71
- 被引次数: 0
