网站地图
-
垂直腔半导体光器件具备体积小、功耗低、易于集成等优点，历来受到人们的重视[1-5]。其中，垂直腔半导体光放大器(vertical cavity semiconductor optical amplifier，VCSOA)可以看作是偏置在阈值电流以下(但非常接近)工作的激光器，它可以对入射光进行法布里-珀罗(Fabry-Perot, F-P)放大。前期的研究工作表明，作为光放大器，入射端面反射率对VCSOA的增益以及饱和输出特性有重要影响；应用于慢光时，VCSOA的时延带宽积也与入射端面反射率密切相关。因此在VCSOA设计制作中，准确控制其端面反射率，对于优化VCSOA在不同应用中的性能，是至关重要的[6-10]。
VCSOA中由多层高、低折射率交替的膜堆构成的分布布喇格反射器(distributed Bragg reflector，DBR)来提供光反馈，DBR膜堆结构决定了它的端面反射率。正入射条件下，DBR的反射率是易于计算的。但是，VCSOA腔长很短，入射到DBR上的很大一部分光是不满足正入射条件的，这样正入射条件下计算出的DBR反射率必然有偏差。所以，考虑到VCSOA内部光场分布特点，本文中将结合角谱理论和传输矩阵法来计算分析VCSOA中DBR的等效反射率。从VCSOA内部发出的光，入射到DBR上的角频谱近似服从高斯分布，首先采用传输矩阵法计算各个角频谱分量的等效反射系数，然后对反射的角频谱进行傅里叶逆变换得到反射光场分布。入射光场和反射光场一旦确定, 就可以利用它们之间的耦合关系计算出等效反射率。
计算结果表明，与只考虑正入射情况相比，修正的DBR等效反射率小了2%~4%。对于激光器而言，因为制作时可以增加DBR膜堆的层数以确保高的反射率，降低器件阈值电流，所以正入射计算误差并未引起人们的重视。但是对于放大器而言，出发点不再是降低器件阈值电流，而需要根据不同应用需求，优化设计端面反射率的大小，这样，准确计算膜堆层数对DBR等效反射率的影响就成为前提条件，这正是作者工作的动机和出发点[11-16]。
-
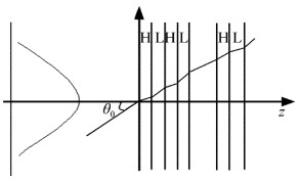
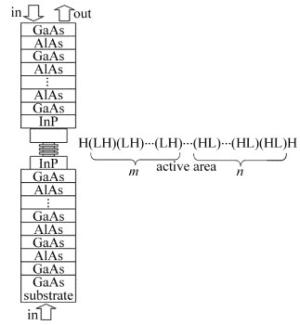
VCSOA的微腔结构的形式是用高折射率层与有源区相邻，再接以低折射率层组成一个HL周期，两侧分别连接m个和n个周期，最后再接一个H层结束，形成(HL)(HL)…(HL)H结构，这种结构简称为HLH结构[17]，如图 1所示。
Figure 1. Schematic diagram of VCSOA
根据光学薄膜原理，多层介质膜第j层的特征矩阵Mj为[18]:
$ {\mathit{\boldsymbol{M}}_j} = \left[ \begin{array}{l} \cos {\delta _j}\;\;\;\frac{{\rm{i}}}{{{\eta _j}}}\sin {\delta _j}\\ {\rm{i}}{\eta _j}\sin {\delta _j}\;\;\cos {\delta _j} \end{array} \right] $
(1) 式中，λ是光波波长，dj为该层厚度，nj为该层折射率，θj为入射角度，i为虚数单位, δj=2π/(λnjdjcosθj)，ηj对于p偏振时为ηj=nj/cosθj，对于s偏振是ηj=njcosθj。本文中所用的薄膜厚度为1/4波长, 即dj=λ/4。整个DBR的传输矩阵M为:
$ \mathit{\boldsymbol{M = }}{\left( {{\mathit{\boldsymbol{M}}_{\rm{H}}}{\mathit{\boldsymbol{M}}_{\rm{L}}}} \right)^m}{\mathit{\boldsymbol{M}}_{\rm{H}}} $
(2) 式中，m表示DBR结构周期。
$ \left[ \begin{array}{l} \mathit{\boldsymbol{B}}\\ \mathit{\boldsymbol{C}} \end{array} \right] = \mathit{\boldsymbol{M}}\left[ \begin{array}{l} \;\;1\\ {\eta _{k + 1}} \end{array} \right] $
(3) 式中，k+1层为衬底层，B和C分别为膜层和基板的组合特征矩阵。
于是可以得到DBR多层介质膜的等效导纳Y=C/B, 则膜系的Fresnel反射系数r和反射率R为：
$ r = \frac{{{\eta _0} - Y}}{{{\eta _0} + Y}} $
(4) $ R = \left( {\frac{{{\eta _0} - Y}}{{{\eta _0} + Y}}} \right){\left( {\frac{{{\eta _0} - Y}}{{{\eta _0} + Y}}} \right)^*} $
(5) 式中，*表示共轭。利用这种方法，可以得到注入光的DBR等效反射率。
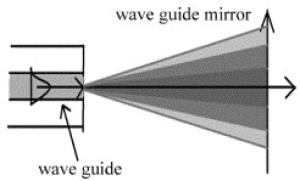
在VCSOA中有源腔内，光以一定的角度θ0入射到DBR面上[17], 如图 2所示。
Figure 2. Internal light field distribution map of VCSOAs
入射场角频谱Fi(s)可以认为服从标准高斯分布:
$ {F_{\rm{i}}}\left( s \right) = A\exp \left[ { - \frac{1}{2}{{\left( {\frac{s}{{{\sigma _0}}}} \right)}^2}} \right] $
(6) 式中，A为高斯函数的幅值，s=sinθ0，θ0是入射角。该分布的半峰全宽(full width at half maxima，FWHM)σ定义为幅度降低一半时对应的s，即${s_{{\rm{FWHM}}}} = \sqrt {2\ln 2} {\sigma _0} $=1.1774σ0, σ0为正态分布的方差。则对应θ0的θFWHM=2arcsin(sFHWM)= 2arcsin(1.1774σ0)。
对(6)式进行傅里叶逆变换, 得到入射光场分布：
$ {E_{\rm{i}}}\left( x \right) = A\frac{1}{{\sqrt {2{\rm{ \mathit{ π} }}} }}{\sigma _0}\exp \left( { - \frac{1}{2}{\sigma _0}^2{x^2}} \right) $
(7) 根据菲涅耳反射定律，反射场的角频谱Fref(s)为：
$ {F_{{\rm{ref}}}}\left( s \right) = r\left( {{\theta _0}} \right){F_{\rm{i}}}\left( s \right) $
(8) 式中，r(θ0)为菲涅耳反射系数。
对Fref(s)进行傅里叶逆变换, 得到z=0处的反射场Eref(x)。
反射场Eref(x)和入射场Ei(x)相干叠加，耦合系数的平方的比就是反射率R[19-20]:
$ R = \frac{{{{\left| {\smallint _{ - \infty }^\infty {E_{\rm{i}}}\left( x \right){E_{{\rm{ref}}}}\left( x \right){\rm{d}}\mathit{x}} \right|}^2}}}{{{{\left| {\smallint _{ - \infty }^\infty E_{\rm{i}}^2\left( x \right){\rm{d}}x} \right|}^2}}} $
(9) -
光波在DBR处被反射，同时一部分向自由空间输出, 如图 3所示。
Figure 3. Emission from the facet
输出光场的角频谱Fo(s)为：
$ {F_{\rm{o}}}\left( s \right) = t\left( {{\theta _0}} \right){F_{\rm{i}}}\left( s \right) $
(10) 式中，t(θ0)为菲涅耳透射系数。
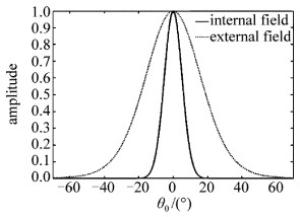
从参考文献[16]中知道，一般半导体激光器的出光孔径为2μm~17μm时，远场扩散角度的半值谱宽为30°~7°。而对于垂直腔激光放大器，出光孔径更小，为1μm左右。远场扩散角的半值谱宽为40°左右。图 4中给出了远场扩散角的半值谱宽为38°时的内外角频谱分布图，纵坐标为相对值。由点线模拟结果可以知道，此时腔内角频谱Fi(s)的半值谱宽θFWHM=12°，σ0=0.09。拟合出来的结果与韩国公司生产的型号为RayCan RC32xxx1-Fd的光器件完全一致。
Figure 4. Relationship between amplitude and the biased angle
-
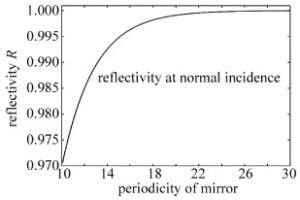
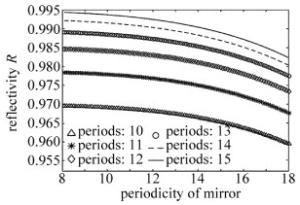
表 1为各膜层折射率。图 5中给出了在正入射的情况下，利用传输矩阵法计算出的GaAs/AlAs结构的DBR反射率随周期数变化曲线。从图中可以看出, 随着DBR结构周期数的增加，腔反射率逐渐增加。VCSOA的一个DBR作为出光面，既要保证有一定的腔反射率用于形成谐振，又要使激射波长有一定的腔透射率用于形成激光输出；而另一个面作为反射面，主要考虑增大反射率从而使腔内有更高的增益。所以一般VCSOA的双层DBR结构并不对称。当结构周期大于25时，中心激射波长处的反射率接近1，并且基本已经不再随周期增大而改变，所以VCSOA反射面的DBR周期一般选取为25左右。而出光面的周期则既要考虑谐振，又要考虑激射波长，因而需要适当地选取。通常此类VCSOA产品出光面的DBR周期选为13。
Table 1. Refractive index
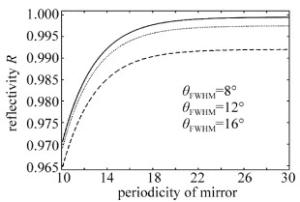
VCSOA refractive index DBR(GaAs) 3.45 DBR(AlAs) 2.89 active area (InAs0.5P0.5) 3.36 active area (In0.8Ga0.2P) 3.30 active area (InP) 3.17 base area (GaAs) 3.45 
Figure 5. Relationship between reflectivity and periodicity of DBR
图 6中给出了考虑光场分布时，采用角频谱分析法计算出的反射率随着DBR结构周期的变化关系曲线。从计算结果可以看出，VCSOA中DBR等效反射率和光场分布有一定的关系。在一定的光场分布下，等效反射率的变化趋势和正入射时利用传输矩阵法的结果是一致的。等效反射率都随着结构周期增加而增加，且当DBR结构周期大于25时基本不再增长。在以上的分析中，作者已经提到本文中VCSOA中入射到DBR上角频谱分布的半值谱宽θFWHM一般在12°左右。图 7中给出了两者的对比情况。可以看出，当腔内角频谱分布的半值谱宽θFWHM为12°时，在同一结构周期下，VCSOA中DBR的等效放射率要比直接利用正入射的模型计算小2%~4%。这在分析VCSOA工作特性时是至关重要的。图 6中还给出了θFWHM为8°和16°时，等效反射率随结构周期的变化情况。
Figure 6. Relationship between reflectivity and periodicity of DBR at different θFWHM
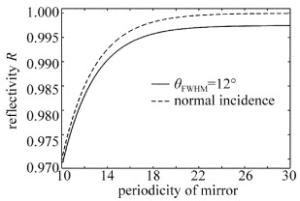
Figure 7. Relationship between reflectivity and periodicity of DBR under θFWHM=12° and normal incidence
图 8中给出了DBR等效反射率随光场分布的关系。在同一结构周期下，等效反射率在正入射θFWHM=0°时最大，并随着θFWHM变大而逐渐降低。从图中看出, 当光场分布比较集中(θFWHM < 8°)时，等效反射率和正入射时相当。(结构周期为13时，等效反射率为0.985)。此时的光相当于正入射到DBR上，光场失谐不大，对等效反射率影响较小。随着半值谱宽增加，入射场和反射场的失谐程度越大，等效反射率越低。考虑光场分布的影响后，同一结构周期的等效反射率降低了2%~4%。当周期为13、且θFWHM=12°时，等效反射率R=0.97。当腔内光场分布更不集中的情况下，等效反射率更低。
Figure 8. Relationship between reflectivity and θFWHM at different periods of DBR
-
本文中利用角频谱分析法，结合传输矩阵计算了VCSOA中DBR的等效反射率。等效反射率随着结构周期增加而变大，但是当周期大于25时基本不再变化。分析了等效反射率和光场分布的关系。在同一结构周期下，考虑光场分布时的等效反射率和正入射变化趋势相同，但是要小2%~4%。等效反射率随着半值谱宽θFWHM增大而减小。这为准确计算膜堆层数对DBR等效反射率的影响提供了理论指导，可进一步优化VCSOA的工作性能，例如降低阈值、优化增益带宽积等。
垂直腔半导体光放大器中的等效反射率分析
Analysis of equivalent reflectivity of vertical-cavity semiconductor optical amplifiers
-
摘要: 为了优化垂直腔半导体光放大器（VCSOA）在不同应用中的性能，以及用通用计算方法获得准确的端面反射率，考虑到器件内部光场分布特点，采用角频谱理论和传输矩阵的方法，取得了器件中分布布喇格反射器（DBR）等效反射率与光束半值谱宽的数据，进行了理论分析和实验验证。结果表明，等效反射率随着结构周期增加而变大，但是当周期大于25时基本不再变化；与只考虑正入射情况相比，修正后的DBR等效反射率小了2%~4%；等效反射率随着半值谱宽θFWHM增大而减小。该研究为准确计算膜堆层数对DBR等效反射率的影响提供理论指导，优化了VCSOA的工作性能。Abstract: In order to optimize the performance of vertical cavity semiconductor optical amplifiers (VCSOA) in different applications and obtain accurate reflectivity with the general calculation method, considering the characteristics of light field distribution inside the device, the equivalent reflectivity of the distributed Bragg reflector (DBR) and the full width at half maximum of the beam in the device were obtained by using angular spectrum theory and transmission matrix method.The theoretical analysis and experimental verification were carried out.The results show that the equivalent reflectivity increases with the increase of structure period.However, when the period is greater than 25, it will not change any more.Compared with the case of normal incidence only, the revised equivalent reflectivity of DBR is less 2%~4%.Equivalent reflectance decreases with the increase of full width at half maximum θFWHM.The study provides theoretical guidance for accurately calculating the effect of stack number on equivalent reflectivity of DBR and optimizing the performance of VCSOA.
-
Figure 7. Relationship between reflectivity and periodicity of DBR under θFWHM=12° and normal incidence
Table 1. Refractive index
VCSOA refractive index DBR(GaAs) 3.45 DBR(AlAs) 2.89 active area (InAs0.5P0.5) 3.36 active area (In0.8Ga0.2P) 3.30 active area (InP) 3.17 base area (GaAs) 3.45 
下载: 导出CSV
-
[1] SAHRAEE E, ZARIFKAR A, SANAEE M. Improvement of gain recovery in QD-VCSOA at 1Tb/s cross gain modulation using an additional light beam[J]. IEEE Journal of Quantum Electronics, 2014, 50(10):1-7. [2] QASAIMENH O. Novel tunable bistable quantum-dot vertical-cavity semiconductor optical amplifier[J]. IEEE Photonics Technology Le-tters, 2016, 28(14):1553-1556. doi: 10.1109/LPT.2016.2558520 [3] PIPREK J, BJǒRLIN E S, BOWERS J E. Design and analysis of vertical-cavity semiconductor optical amplifiers[J]. IEEE Journal of Quantum Electronics, 2008, 37(1):127-134. [4] QASAIMENH O. Simple semi-analytical model for bistable cross-gain modulationg in quantum dot VCSOAs[J]. Optical & Quantum Electronics, 2017, 49(9):309. [5] ADAMS M J, COLLINS J V, HENNING I D. Analysis of semiconductor laser optical amplifiers[J]. IEEE Proeecdings, 2000, 132(1):58-63. [6] IGA K. Vertical-cavity surface-emitting laser:Its conception and evolution[J]. Japanese Journal of Applied Physics, 2008, 47(1):1-10. doi: 10.1143/JJAP.47.1 [7] SAHRAEE E, ZARIKAR A. MEMS-based tuning of InGaAs/GaAs quantum dot-VCSOA[J]. IEEE Journal of Quantum Electronics, 2015, 51(5):1-10. [8] QASAIMENH O. Cross-gain modulation in bistable quantum-dot VCSOAs[J]. IEEE Photonics Technology Letters, 2017, 29(3):342-345. doi: 10.1109/LPT.2016.2647591 [9] LI B Zh, ZOU Y G. Tunable vertical cavity surface emitting lasers[J]. Laser Technology, 2018, 42(4):556-561(in Chinese). [10] MA Y N, LUO B, PAN W, et al. Improvement of slow light performance for vertical-cavity surface-emitting laser using coupled cavity structure[J]. Optoelectronics Letters, 2012, 8(6):0405-0408. doi: 10.1007/s11801-012-2302-x [11] LU J, LUO B, ZHOU G, et al. Analysis of tune output property of vertical-cavity semiconductor optical amplifiiers[J]. Laser Techno-logy, 2011, 35(2):260-263(in Chinese). [12] QIN Zh M, LUO B, PAN W. Theoretical analysis of the gain of vertical cavity semiconductor optical amplifier[J]. Laser Technology, 2006, 30(5):452-454(in chinese). [13] ZHANG W L, YU S F. Bistabilities of birefringent vertical-cavity semiconductor optical amplifiers with antiresonant reflecting optical waveguide[J]. IEEE Journal of Quantum Electronics, 2010, 46(1):11-18. doi: 10.1109/JQE.2009.2022651 [14] ZHANG Y, GUAN B O, TAM H Y. Characteristics of the distributed Bragg reflector fiber laser sensor for lateral force measurement[J]. Optics Communications, 2008, 281(18):4619-4622. doi: 10.1016/j.optcom.2008.05.039 [15] MA Y N, LUO B, PAN W, et al. Capability limitatioin for slow light using vertical-cavity surface-emitting laser amplifier[J]. IEEE Photonics Technology Letters, 2013, 25(10):903-906. doi: 10.1109/LPT.2013.2253546 [16] BJÖRLINS, RIOU B, KEATING A, et al. 1.3μm vertical-cavity amplifier[J]. IEEE Photonics Technology Letters, 2000, 12(8):951-953. doi: 10.1109/68.867971 [17] ZHANG C Sh, ZHANG Y Sh, DU A F, et al. Analysis of reflectance characteristics of DBR in vertical cavity surface emitting lasers[J]. Journal of Optoelectronics·Laser, 2002, 13(1):34-36(in Chinese). [18] GAI H X, GUO X, DENG J, et al.Study of the optical characteristic of the vertical surface emitting laser using optical thin_film model[J]. Optical Technique, 2005, 31(6):904-909(in Chinese) [19] DIAS N L, REDDY U, GARG A, et al.Wide stripe distributed bragg grating lasers with very narrow spectral linewidth[J]. IEEE Journal of Quantum Electronics, 2014, 47(3):293-299. [20] ZIMMERMAN J W, PRICE R K, REEDY U, et al. Narrow linewidth surface-etched DBR laser:Fundamental design aspects and applications[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2014, 19(4):1503712. -
点击查看大图
图(8) / 表(1)
计量
- 文章访问数: 7631
- HTML全文浏览量: 5571
- PDF下载量: 93
- 被引次数: 0
