网站地图
-
表面裂纹大量存在于长期处于交变载荷下的金属构件中，裂纹的存在会导致机器致命性的损坏，并且引发安全问题，因此如何快速、便捷、准确地识别并定位出表面裂纹是当前无损检测的一个热点。由于传统的无损检测技术(如磁粉检测、电涡流检测)不适用于恶劣环境，而激光超声检测技术以其时空分辨率高、信号带宽宽、无损坏、非接触等优点，在无损检测领域得到广泛的应用[1-3]。为了研究激光超声的产生、传播过程以及表面裂纹的检测机理，近十几年来，国内外很多学者进行了大量的研究，特别是利用激光激发出的瑞利波检测表面裂纹的特征，并取得了重大的研究成果[4-11]。但是工程领域中, 为了提高金属构件表面的硬度以及耐磨性等性能，通常会在构件表面镀上不同材料及厚度的涂层，这些涂层的存在使得瑞利波的产生机理与传播更为复杂。虽然有学者研究了涂层/基底系统中激光激发的瑞利波[12-15]，但是很少有人研究激光激发的瑞利波与带涂层金属表面裂纹相互作用下的规律。
作者采用数值模拟的方法，通过对模拟得到的瑞利波时域信号进行短时傅里叶变换与傅里叶变换，分别研究了在镍涂层下的涂层厚度、裂纹深度与瑞利波时频域信号的关系, 为通过瑞利波的时域特征定量表征裂纹的深度提供了参考。
-
为了使计算出的数据更接近真实情况，将脉冲激光的作用等效成热力源的形式。由于脉冲激光的能量符合高斯分布，材料吸收的能量Q(r, z, t)表示为：
$ Q\left( r, z, t \right)={{I}_{0}}Af\left( r \right)g\left( t \right) $
(1) 对于高斯热源，有：
$ f(r)=\text{exp}(-\frac{{{r}^{2}}}{r_{0}^{2}})~ $
(2) $ g\left( t \right)=\frac{t}{\tau }~\text{exp}(-\frac{t}{\tau }) $
(3) 式中, A为材料对激光的吸收系数，I0为激光峰值功率密度，f(r)为脉冲激光的空间分布，g(t)为脉冲激光的时间分布, r是空间半径, z是z方向长度, t是时间。计算中取激光波长λ =1064nm，脉冲上升时间τ=10ns，光斑半径r0=300μm，单脉冲能量E0=13.5mJ。
-
当线源激光沿宽度方向均匀照射到板上时，该问题可以简化为一个2维的平面问题，又由于入射激光束光斑具有轴对称分布的特性，因此所有数值计算都是基于2维轴对称模型。数值计算过程中，取带涂层铝板的长度L=12mm，总厚度ha=10mm(含涂层)，裂纹距离激光束作用中心dc=8mm。信号接收点距离缺陷左边沿d的值分别为0mm，2mm，4mm，6mm，对应点简称为A，B，C，D。模型如图 1所示。
Figure 1. Model diagram
为了精确计算出温度场的分布以及模拟激光激发出的超声波在模型内的传播过程，本文中采用变网格方法，在激光作用区域和缺陷区域采用10μm的密网格，在远离激光作用区域采用90μm的松网格，网格如图 2所示。
Figure 2. Schematic diagram of finite element grid division
-
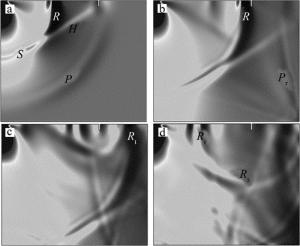
分别建立涂层厚度h为0μm(无涂层)和100μm、裂纹深度hc均为500μm、缺陷距离激光辐射中心dc均为8mm的模型，并进行数值模拟，得到激光照射后不同时刻的全场位移，如图 3和图 4所示。从图 3a和图 4a可以清晰地区分激光激发出的头波H、纵波P、横波S和瑞利波R，并看到其能量的差别，其中瑞利波能量较大；从图 3b和图 4b可以看到界面反射纵波Pr; 图 3c和图 4c是透射瑞利波Rt；图 3d和图 4d是瑞利波与缺陷作用后的反射瑞利波Rr和模式转换得到的剪切波Rs。从图 3和图 4可以看出, 带涂层与无涂层模型的瑞利波在相同时刻到达位置不同，即波速不同；由于涂层对能量的衰减，带涂层的模型中所有波的幅值都有所降低；带涂层的瑞利波后面紧跟着更多频率的波，出现了色散；带涂层模型的负向位移被缺陷反射的掠面纵波正向位移抵消了一部分，因此带涂层的Rr波负向位移值较小。以上表明, 该数值模型可以有效模拟出激光激发的声波以及瑞利波与缺陷作用的过程，为进一步分析瑞利波与裂纹的相互作用奠定基础。
Figure 3. Full-field displacement diagram with 0μm thickness coating model at different moments
Figure 4. Full-field displacement diagram with 100μm thickness coating model at different moments
-
为研究镍涂层对激光激发出的瑞利波信号的影响，在裂纹深度hc=0μm的前提下取不同厚度的涂层进行数值模拟。当h分别为0μm和100μm、接收点为A时，时域信号如图 5所示。
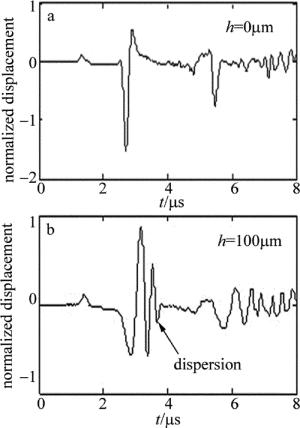
Figure 5. The influence of different coating thickness models on time domain signals of the receiving point A
从图 5中看到，无涂层模型瑞利波到达时间为2.67μs，带100μm涂层模型的瑞利波到达时间为2.95μs，即镍涂层的存在影响了瑞利波的传播速度。这是因为瑞利波的高频成分因波长短透入深度浅，低频成分因波长长透入深度深，因此大部分高频成分在镍涂层内传播，低频成分在基底铝内传播；又由于铝的瑞利波速度比镍的快，因此高频成分相对于低频成分传播得慢，导致在带100μm涂层模型上的瑞利波在3.7μs时刻出现一定的色散，如图 5b所示。对上述信号进行短时傅里叶变换，得到图 6。从图 6a中可以看到, 对于涂层厚度为0μm的模型，无论高频还是低频的分布都集中在一个时间段内；从图 6b中可以看到, 当涂层厚度为100μm时，低频成分比高频成分出现得更早，因此图 6同样说明高频成分传播速度比低频成分慢，存在着色散。
Figure 6. The results of short-time Fourier transform of time domain signal of different coating thickness models at the receiving point A
-
表 1中给出了在不同涂层厚度、接收点C和D的瑞利波到达时间。通过表中数据算出对应波速，并取其平均值，采用B样条插值方法拟合出波速和涂层厚度的曲线图，如图 7所示。
Figure 7. Relationship between Rayleigh wave velocity and coating thickness h
表 1 Arrival time of Rayleigh wave at different receiving points and coating thickness h
coating
thickness h/μm0 50 100 150 200 250 300 350 400 450 500 550 D/μs 0.652 0.716 0.776 0.800 0.796 0.788 0.776 0.772 0.752 0.746 0.736 0.728 C/μs 1.344 1.444 1.588 1.636 1.636 1.620 1.608 1.588 1.572 1.548 1.532 1.524 从图 7中可以看出，瑞利波的波速从接近基底铝的瑞利波波速开始，随着涂层厚度的增大，减小到最小值，然后逐渐增大为趋近涂层镍的瑞利波波速。为分析带涂层金属表面裂纹深度hc与Rr和Rs到达时间差Δt的关系提供了参考。
-
图 8中给出了无涂层、信号接收点B处0μm裂纹和300μm裂纹的声表面波时域波形。可以看到，当表面存在裂纹时，除了R波峰外，会多出两个明显的特征波峰Rr波峰和Rs波峰。
Figure 8. Rayleigh wave time domain waveform of uncoated 0μm crack and 300μm crack
图 9为上述时域信号经过快速傅里叶变换得到的频域信号。为解决频域分辨率较低的问题，这里采用了局部的傅里叶变换的方法，加窗位置为1.6μs~5.6μs。观察频域波形发现，有裂纹时的频谱幅度有微量的增强，这是由于缺陷的存在，使传播到缺陷位置处的声表面波发生反射，致使接收到的声表面波的总体能量变大所造成的。
Figure 9. Rayleigh wave frequency domain signal of uncoated 0μm crack and 300μm crack
-
图 10中分别给出了0μm, 200μm, 400μm的涂层厚度模型接收点B处的Rs波与Rr波到达时间差Δt与裂纹深度hc的关系。从图 10中可以看到, 对于0μm涂层厚度模型，Δt与hc呈现出线性关系；对于200μm和400μm涂层厚度模型，Δt与hc在整体上是非线性的关系，但是它们都以各自涂层厚度为分界点的分段线性关系。这是因为当缺陷深度hc小于涂层厚度h时，Rs波大部分都在涂层内传播；当hc大于涂层厚度时，Rs波首先在基底铝内传播，然后在镍涂层内传播，两者属于不同的介质，因此导致不同的线性关系。
Figure 10. Relationship between Δt and hc at different coating thickness
-
作者建立了带涂层金属表面裂纹的有限元数值模型，研究了涂层厚度对瑞利波波速的影响，以及瑞利波时域特征与表面裂纹深度之间的关系。
(1) 当涂层厚度从0μm增加到500μm时，瑞利波波速逐渐减小到一个极小值，再逐渐增大为接近涂层的瑞利波波速。
(2) 无涂层模型的Rr波与Rs波的到达时间差与裂纹深度成线性关系，有涂层模型的Rr波与Rs波的到达时间差与裂纹深度以涂层厚度为分界点成分段线性关系。
(3) 涂层的存在降低了激光激发出的波的幅值，且Rr波的负极性被缺陷反射回来的掠面纵波正极性抵消，幅值被极大地衰弱。
以上结论为激光超声无损检测的实际测量提供了一种参考。
激光超声检测带涂层金属表面裂纹的数值研究
Numerical study on coated metal surface crack by laser ultrasonic detection
-
摘要: 为了研究线源脉冲激光激发的超声波在带涂层金属板表面裂纹检测方面的应用，采用有限元模拟的方法，分别建立了含有裂纹的带镍涂层和不带镍涂层金属板模型，并模拟出激光激发出的瑞利波以及瑞利波的传播过程。通过对接收点处的波形进行理论分析，得出了涂层厚度、裂纹深度与瑞利波时频域信号的关系。结果表明，瑞利波波速随着涂层厚度h的不同而不断变化；当表面存在裂纹时，不带涂层模型的反射瑞利波与剪切瑞利波的到达时间差Δt与裂纹深度hc成线性关系，带涂层模型的Δt与hc以涂层厚度为分界点成分段线性关系。此研究结果为实际测量带涂层金属板的表面裂纹深度提供了参考。Abstract: In order to study the application of ultrasonic wave induced by line-source pulse laser on surface crack detection of the coated metal plate, finite element simulation method was used to establish the model of metal plate with cracks with and without nickel coating. Rayleigh wave excited by laser and the propagation process of Rayleigh wave were simulated. Through theoretical analysis of waveform at the receiving point, the relationship of coating thickness, crack depth and Rayleigh wave time-frequency domain signal was obtained. The numerical results show that Rayleigh wave velocity varies with the thickness of coating thickness h. When there are cracks on the surface, the arriving time difference Δt between reflection Rayleigh wave and shear Rayleigh wave of the model without coating has linear relationship with crack depth hc. Δt of the model with coating has linear relationship with crack depth hc at different segmentations. The numerical results provide reference for actual measurement of the surface crack depth of metal sheets with coating.
-
Key words:
- measurement and metrology /
- laser ultrasonic /
- Rayleigh wave /
- rack detection /
- nickel coating
-
Figure 3. Full-field displacement diagram with 0μm thickness coating model at different moments
a—t=1.53μs b—t=2.58μs c—t=3.63μs d—t=4.52μs
Figure 4. Full-field displacement diagram with 100μm thickness coating model at different moments
a—t=1.53μs b—t=2.58μs c—t=3.63μs d—t=4.52μs
Figure 5. The influence of different coating thickness models on time domain signals of the receiving point A
Figure 6. The results of short-time Fourier transform of time domain signal of different coating thickness models at the receiving point A
表 1 Arrival time of Rayleigh wave at different receiving points and coating thickness h
coating
thickness h/μm0 50 100 150 200 250 300 350 400 450 500 550 D/μs 0.652 0.716 0.776 0.800 0.796 0.788 0.776 0.772 0.752 0.746 0.736 0.728 C/μs 1.344 1.444 1.588 1.636 1.636 1.620 1.608 1.588 1.572 1.548 1.532 1.524 
下载: 导出CSV
-
[1] MA J, ZHAO Y, ZHOU F Y. Effect of defocusing amount on thickness measurement based on laser ultrasound[J]. Laser Technology, 2015, 39(3):349-352(in Chinese). [2] LIU P P, NAZIRAH A W, SOHN H. Numerical simulation of damage detection using laser-generated ultrasound[J]. Ultrasonics, 2016, 69:248-258. doi: 10.1016/j.ultras.2016.03.013 [3] ZHAN Y, LIU Ch Sh, ZHANG F P, et al. Experimental study and finite element analysis based on equivalent load method for laser ultrasonic measurement of elastic constants[J]. Ultrasonics, 2016, 69:243-247. doi: 10.1016/j.ultras.2016.03.014 [4] GUAN J F. Numerical analysis of inspection of micro-surface crack by laser generated surface acoustic waves[J]. Chinese Journal of Quantum Electronics, 2011, 28(3):362-368(in Chinese). [5] SONG Y X, WANG J. The influence of laser parameters and laser ultrasonic detection methods on ultrasonic signals[J]. Infrared and Laser Engineering, 2014, 43(5):1433-1437(in Chinese). [6] ZENG W, WANG H T, TIAN G Y, et al. Study on the oscillation effects of laser-induced SAW and near-surface defects[J]. Chinese Journal of Physics, 2015, 64(13):134302(in Chinese). [7] GUO H L, ZHENG B, LIU H. Numerical simulation and experimental research on interaction of micro-defects and laser ultrasonic signal[J]. Optics and Laser Technology, 2017, 96:58-64. doi: 10.1016/j.optlastec.2017.04.004 [8] XU B Q, SHEN Z H, LU J. Numerical simulation of laser-induced transient temperature field in film-substrate system by finite element method[J]. International Journal of Heat and Mass Transfer, 2003, 46(25):4963-4968. doi: 10.1016/S0017-9310(03)00345-4 [9] WANG M Y, ZHOU Y J, GUO Ch. Numerical simulation of laser ultrasonic detection of surface micro-crack depth[J]. Laser Technology, 2017, 41(2):178-181(in Chinese). [10] LIU H, ZHEN B, WANG Zh B, et al.Time dependence of laser Rayleigh wave on detecting surface defect depth[J]. Laser & Infrared, 2017, 47(6):669-673(in Chinese). [11] MA J, ZHAO Y, GUO R, et al. Numerical simulation of temperature rise of material surface irradiated by the laser[J]. Laser Technology, 2013, 37(4):455-459(in Chinese). [12] XU B Q, SHEN Zh H, NI X W, et al. Thermal and mechanical finite element modeling of laser-generated ultrasound in coating-substrate system[J]. Optics and Laser Technology, 2006, 38(3):138-145. doi: 10.1016/j.optlastec.2004.12.002 [13] WANG J J, SHEN Zh H, NI X W, et al. Numerical simulation of laser-generated surface acoustic waves in the transparent coating on a substrate by the finite element method[J]. Optics and Laser Technology, 2007, 39(1):21-28. doi: 10.1016/j.optlastec.2005.05.015 [14] SHEN Zh H, YUAN L, ZHANG H Ch, et al. Laser ultrasound in solids[M]. Beijing:Post & Telecom Press, 2015:57-68(in Chinese). [15] XU B Q, SHEN Zh H, NI X W, et al. Time-frequency analysis of laser-generated ultrasonic wave in coating-substrate systems[J]. Laser Technology, 2004, 28(6):609-612(in Chinese). -
点击查看大图
图(10) / 表(1)
计量
- 文章访问数: 6281
- HTML全文浏览量: 4005
- PDF下载量: 160
- 被引次数: 0
