网站地图
-
光载微波雷达是以射频强度调制激光作为载波进行测距测速和成像的新型激光雷达，兼具激光雷达的体积小、机动灵活、空间分辨率高的特点，以及微波雷达的抗大气干扰能力强的优势。在水下探测中，强度调制载波配合带通滤波技术可以有效抑制海水及其中的悬浮物对信号的散射带来的噪声干扰，提高系统信噪比、对比度和作用距离，在海洋探测领域有着很大的应用潜力[1-2]。
射频强度调制光源的实现方法有多种，其中最简单直接的就是使用电光调制器进行强度调制，调制频率可以从几十兆赫兹到千兆赫兹[3-4]，但是被调制光波的功率通常不能太高，且高频调制的调制度也不会太深。两束光干涉也可以得到强度调制光，其中正交偏振双频激光是实现强度射频调制光源的一种方法，利用该方法可以达到100%的调制度，但是其输出的差频信号的频率往往不稳，将激光器输出频率稳定在千赫兹水平是很困难的[5-9]。另一种方法是利用声光移频合束来实现射频强度调制光波，其差频信号的稳定性取决于射频(radio frequency, RF)驱动源的频率稳定性，可以通过调节两个参加干涉光的功率比来实现不同的调制深度[10]。但是这种方法可实现的频差范围限制在几百兆的范围内，频率更高，声光器件实现起来将会有较大难度。所以, 选择哪种实现载波强度调制的方式要根据具体的应用场景来确定，在调制深度和频率之间进行折中选择。
与单频激光信号相比，双频信号具有更强的抗大气干扰能力[11]，而调制深度会对双频信号的抗大气扰动的能力产生一定的影响，这方面的理论研究和实验验证还鲜有报道。本文中采用干涉的方法对RF强度调制信号的调制深度对其抗大气干扰能力的影响做了深入的研究。搭建了Mach-Zehnder干涉仪，参加干涉的两束光分别为未经调制的单频光和调制后的双频光。以干涉条纹对比度作为信号相位起伏的衡量标准，比较了不同大气湍流干扰条件下，干涉条纹的对比度随调制深度的变化。大气湍流由空间光调制器模拟产生。建立了相应的理论模型，对实验结果进行了解释，研究结果对双频相干探测光源的选择具有一定的参考意义。
-
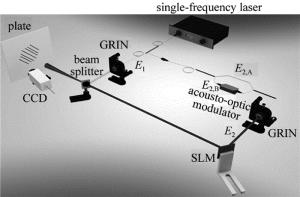
双频激光抗大气干扰实验的系统结构如图 1所示。系统包括光源、大气湍流模拟装置和图像信息处理3个部分。
Figure 1. System structure of anti-atmospheric interference experiment with dual frequency laser
将1064nm的窄线宽低噪声单频激光源输出分为两束:其中一束作为一路干涉光; 另一束利用移频自差法获得双频激光，频差为200MHz的双频激光束作为干涉的另一路探测光。
两路干涉光分别通过自聚焦透镜(graded index lens, GRIN)准直，在双频激光的光路中放置BNS公司的空间光调制器(spatial light modulator, SLM)来模拟大气湍流引起的随机相位扰动。SLM为反射式器件，由512×512个微反射镜组成。通过输入模拟大气湍流的相位灰度值作为输入信号控制该反射式SLM的镜面形状来改变光束波前相位，从而达到模拟大气湍流干扰的效果。干涉条纹成像在干涉板上，通过CCD拍摄干涉图像，最后由计算机进行图像处理。
-
如图 1所示，单频激光器出射后分成两束，其中一束作为干涉光E1，另一束通过移频自差法获得双频激光，未移频的一路为E2, A，通过声光移频的一路为E2, B，合束成为E2并经过大气湍流扰动，再与E1进行干涉，得到干涉条纹。为简化推导过程，设单频激光的角频率为ω1，振幅为A1，初相位为0，传输时间为t。双频激光中未移频一路的角频率为ω1，振幅为A2, A，初相位为0，经声光移频一路的角频率为ω2，振幅为A2, B，初相位为0，传输时间为t。令Δω=ω2-ω1，双频激光的两路光经大气湍流后均有相位扰动φ。
单频激光的电场表达式为:
$ {E_1} = {A_1}\exp \left( {{\rm{j}}{\omega _1}t} \right) $
(1) 双频激光中未移频和移频后光的电场表达式分别为:
$ {E_{2,{\rm{A}}}} = {A_{2,{\rm{A}}}}\exp \left[ {{\rm{j}}\left( {{\omega _1}t + \varphi } \right)} \right] $
(2) $ {E_{2,{\rm{B}}}} = {A_{2,{\rm{B}}}}\exp \left[ {{\rm{j}}\left( {{\omega _2}t + \varphi } \right)} \right] $
(3) 则合束后的双频激光表达式为:
$ \begin{array}{*{20}{c}} {{E_2} = {E_{2,{\rm{A}}}} + {E_{2,{\rm{B}}}} = {A_{2,{\rm{A}}}}\exp \left[ {{\rm{j}}\left( {{\omega _1}t + \varphi } \right)} \right] + }\\ {{A_{2,{\rm{B}}}}\exp \left[ {{\rm{j}}\left( {{\omega _2}t + \varphi } \right)} \right]} \end{array} $
(4) 调制深度定义为:
$ \mathit{\boldsymbol{M = }}\frac{{{I_{2,\max }} - {I_{2,\min }}}}{{{I_{2,\max }} + {I_{2,\min }}}} $
(5) 式中，I2, max和I2, min分别为调制光强的最大值和最小值。
双频激光的光强为:
$ \begin{array}{*{20}{c}} {{I_2} = {E_2} \cdot {E_2}^ * = }\\ {\left\{ {{A_{2,{\rm{A}}}}\exp \left[ {{\rm{j}}\left( {{\omega _1}t + \varphi } \right)} \right] + {A_{2,{\rm{B}}}}\exp \left[ {{\rm{j}}\left( {{\omega _2}t + \varphi } \right)} \right]} \right\} \cdot }\\ {\left\{ {{A_{2,{\rm{A}}}}\exp \left[ { - {\rm{j}}\left( {{\omega _1}t + \varphi } \right)} \right] + {A_{2,{\rm{B}}}}\exp \left[ { - {\rm{j}}\left( {{\omega _2}t + \varphi } \right)} \right]} \right\} = }\\ {{A_{2,{\rm{A}}}}^2 + {A_{2,{\rm{B}}}}^2 + {A_{2,{\rm{A}}}}{A_{2,{\rm{B}}}}\exp \left[ {{\rm{j}}\left( {{\omega _1} - {\omega _2}} \right)t} \right] + }\\ {{A_{2,{\rm{A}}}}{A_{2,{\rm{B}}}}\exp \left[ {{\rm{j}}\left( {{\omega _2} - {\omega _1}} \right)t} \right] = }\\ {{A_{2,{\rm{A}}}}^2 + {A_{2,{\rm{B}}}}^2 + 2{A_{2,{\rm{A}}}}{A_{2,{\rm{B}}}}\cos \left[ {\left( {{\omega _2} - {\omega _1}} \right)t} \right] = }\\ {{A_{2,{\rm{A}}}}^2 + {A_{2,{\rm{B}}}}^2 + 2{A_{2,{\rm{A}}}}{A_{2,{\rm{B}}}}\cos \left( {\Delta \omega t} \right)} \end{array} $
(6) 式中, E2*代表E2的共轭，将(6)式代入(5)式得到调制深度为:
$ \begin{array}{*{20}{c}} {M = \frac{{{I_{2,\max }} - {I_{2,\min }}}}{{{I_{2,\max }} + {I_{2,\min }}}} = }\\ {\frac{{4{A_{2,{\rm{A}}}}{A_{2,{\rm{B}}}}}}{{2\left( {{A_{2,{\rm{A}}}}^2 + {A_{2,{\rm{B}}}}^2} \right)}} = \frac{{2{A_{2,{\rm{A}}}}{A_{2,{\rm{B}}}}}}{{{A_{2,{\rm{A}}}}^2 + {A_{2,{\rm{B}}}}^2}}} \end{array} $
(7) 由上式得双频激光中两路光的振幅关系如下:
$ {A_{2,{\rm{B}}}} = \frac{{1 \pm \sqrt {1 - {M^2}} }}{M}{A_{2,{\rm{A}}}} $
(8) 去掉不合理的取值，并令:
$ m = \frac{{1 - \sqrt {1 - {M^2}} }}{M} $
(9) $ {A_{2,{\rm{B}}}} = m{A_{2,{\rm{A}}}} $
(10) 为保证干涉的两路光信号强度相等，即I1=I2，其中单频激光的光强为:
$ \begin{array}{*{20}{c}} {{I_1} = {E_1} \cdot {E_1}^ * = {A_1}\exp \left( {{\rm{j}}{\omega _1}t} \right) \cdot }\\ {{A_1}\exp \left( { - {\rm{j}}{\omega _1}t} \right) = {A_1}^2} \end{array} $
(11) 式中, E1*代表E1的共轭，则有：
$ {A_1}^2 = {A_{2,{\rm{A}}}}^2 + {A_{2,{\rm{B}}}}^2 + 2{A_{2,{\rm{A}}}}{A_{2,{\rm{B}}}}\cos \left( {\Delta \omega t} \right) $
(12) 将(10)式代入(12)式得:
$ {A_1} = {A_{2,{\rm{A}}}}\sqrt {1 + {m^2} + 2m\cos \left( {\Delta \omega t} \right)} $
(13) 经过大气湍流扰动后的双频激光与未加扰动的单频激光发生干涉，光强为:
$ \begin{array}{*{20}{c}} {I = \left( {{E_1} + {E_2}} \right) \cdot {{\left( {{E_1} + {E_2}} \right)}^ * } = }\\ {\left\{ {{A_1}\exp \left( {{\rm{j}}{\omega _1}t} \right) + {A_{2,{\rm{A}}}}\exp \left[ {{\rm{j}}\left( {{\omega _1}t + \varphi } \right)} \right] + } \right.}\\ {\left. {{A_{2,{\rm{B}}}}\exp \left[ {{\rm{j}}\left( {{\omega _2}t + \varphi } \right)} \right]} \right\} \cdot \left\{ {{A_1}\exp \left( { - {\rm{j}}{\omega _1}t} \right) + } \right.}\\ {\left. {{A_{2,{\rm{A}}}}\exp \left[ { - {\rm{j}}\left( {{\omega _1}t + \varphi } \right)} \right] + {A_{2,{\rm{B}}}}\exp \left[ { - {\rm{j}}\left( {{\omega _2}t + \varphi } \right)} \right]} \right\} = }\\ {{A_1}^2 + {A_{2,{\rm{A}}}}^2 + {A_{2,{\rm{B}}}}^2 + {A_1}{A_{2,{\rm{A}}}}\exp \left( { - {\rm{j}}\varphi } \right) + }\\ {{A_1}{A_{2,{\rm{B}}}}\exp \left\{ {{\rm{j}}\left[ {\left( {{\omega _1} - {\omega _2}} \right)t - \varphi } \right]} \right\} + {A_1}{A_{2,{\rm{A}}}}\exp \left( {{\rm{j}}\varphi } \right) + }\\ {{A_{2,{\rm{A}}}}{A_{2,{\rm{B}}}}\exp \left[ {{\rm{j}}\left( {{\omega _1} - {\omega _2}} \right)t} \right] + }\\ {{A_1}{A_{2,{\rm{B}}}}\exp \left\{ {{\rm{j}}\left[ {\left( {{\omega _2} - {\omega _1}} \right)t + \varphi } \right]} \right\} + }\\ {{A_{2,{\rm{A}}}}{A_{2,{\rm{B}}}}\exp \left[ {{\rm{j}}\left( {{\omega _2} - {\omega _1}} \right)t} \right] = }\\ {{A_1}^2 + {A_{2,{\rm{A}}}}^2 + {A_{2,{\rm{B}}}}^2 + }\\ {{A_1}{A_{2,{\rm{A}}}}\left[ {\exp \left( { - {\rm{j}}\varphi } \right) + \exp \left( {{\rm{j}}\varphi } \right)} \right] + }\\ {{A_{2,{\rm{A}}}}{A_{2,{\rm{B}}}}\left\{ {\exp \left[ {{\rm{j}}\left( {{\omega _1} - {\omega _2}} \right)t} \right] + } \right.}\\ {\left. {\exp \left[ {{\rm{j}}\left( {{\omega _2} - {\omega _1}} \right)t} \right]} \right\} + {A_1}{A_{2,{\rm{B}}}}\left( {\exp \left\{ {{\rm{j}}\left[ {\left( {{\omega _1} - } \right.} \right.} \right.} \right.}\\ {\left. {\left. {\left. {\left. {{\omega _2}} \right)t - \varphi } \right]} \right\} + \exp \left\{ {{\rm{j}}\left[ {\left( {{\omega _2} - {\omega _1}} \right)t + \varphi } \right]} \right\}} \right) = }\\ {{A_1}^2 + {A_{2,{\rm{A}}}}^2 + {A_{2,{\rm{B}}}}^2 + }\\ {2{A_1}{A_{2,{\rm{A}}}}\cos \varphi + 2{A_{2,{\rm{A}}}}{A_{2,{\rm{B}}}}\cos \left[ {\left( {{\omega _1} - } \right.} \right.}\\ {\left. {\left. {{\omega _2}} \right)t} \right] + 2{A_1}{A_{2,{\rm{B}}}}\cos \left[ {\left( {{\omega _2} - {\omega _1}} \right)t + \varphi } \right]} \end{array} $
(14) 为简便计算，令A2, A=1，将(10)式和(12)式代入(14)式得:
$ \begin{array}{*{20}{c}} {I = 2{A_{2,{\rm{A}}}}^2 + 2{A_{2,{\rm{B}}}}^2 + 4{A_{2,{\rm{A}}}}{A_{2,{\rm{B}}}}\cos \left( {\Delta \omega t} \right) + }\\ {2{A_1}{A_{2,{\rm{A}}}}\cos \varphi + 2{A_1}{A_{2,{\rm{B}}}}\cos \left( {\Delta \omega t + \varphi } \right) = }\\ {2{A_{2,{\rm{A}}}}^2 + 2{m^2}{A_{2,{\rm{A}}}}^2 + 4m{A_{2,{\rm{A}}}}^2\cos \left( {\Delta \omega t} \right) + }\\ {2{A_1}{A_{2,{\rm{A}}}}\cos \varphi + 2m{A_1}{A_{2,{\rm{A}}}}\cos \left( {\Delta \omega t + \varphi } \right) = }\\ {2 + 2{m^2} + 4m\cos \left( {\Delta \omega t} \right) + }\\ {2{A_1}\cos \varphi + 2m{A_1}\cos \left( {\Delta \omega t + \varphi } \right)} \end{array} $
(15) 下面考虑大气湍流引入的相位扰动项φ，利用功率谱反演法模拟大气湍流畸变的相位屏，其基本原理是将一个复高斯随机数矩阵用大气湍流的功率谱进行滤波，再进行Fourier逆变换产生大气扰动相位起伏矩阵[12-15]。流程如下：(1)首先产生一个复高期随机数矩阵R；(2)构造用空间频率κ作为变量，且符合von Karman谱的功率谱密度矩阵Φφ(κ)；(3)利用步骤(2)得到的von Karman谱对步骤(1)中的R进行滤波，得到矩阵$\mathit{\boldsymbol{R}}\sqrt {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_\mathit{\varphi }}\left(\kappa \right)}$；(4)对矩阵$\mathit{\boldsymbol{R}}\sqrt {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_\mathit{\varphi }}\left(\kappa \right)}$进行Fourier逆变换，取其实部，便得到大气湍流相位屏为Re[IFFT($\mathit{\boldsymbol{R}}\sqrt {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_\mathit{\varphi }}\left(\kappa \right)}$)]。
为了准确模拟出满足大气湍流统计特性的湍流相位屏，需要对相位屏进行低频补偿，即将Fourier高频部分开始的取样部分九等分，每部分为原先采样部分的1/9，形成次谐波网格。将低频和高频部分叠加起来即为总的模拟湍流相位屏。利用MATLAB软件编程模拟出大气湍流相位屏，大气湍流的强度通常是由大气折射率结构常数来表征。在本文的模拟中设定大气折射率结构常数为Cn2=1×10-12m-2/3，得到如图 2所示的较高强度的模拟大气湍流相位屏，其中白色代表相位梯度为0，黑色代表相位梯度为2π。为了便于将模拟得到的大气湍流相位屏灰度图作为空间光调制器(SLM)的输入控制信号，设置相位屏灰度图为512×512像素点，通过输入模拟大气湍流的相位灰度值作为控制信号控制该反射式SLM的镜面形状来改变光束波前相位，从而达到模拟大气湍流干扰的效果。
Figure 2. Phase screen of the simulated atmospheric turbulence
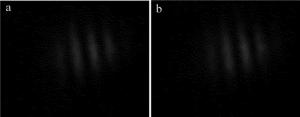
将大气湍流相位屏灰度图作为2维矩阵代入(15)式，得到不同调制深度下的干涉条纹, 如图 3所示。
Figure 3. Interference fringes under strong atmospheric turbulence with diffe-rent modulation depths
干涉条纹的对比度公式为:
$ V = \frac{{{I_{\max }} - {I_{\min }}}}{{{I_{\max }} + {I_{\min }}}} $
(16) 式中, Imax和Imin为条纹最大和最小光强的平均值。因此可以得到调制深度与干涉条纹对比度的关系, 如图 4所示。
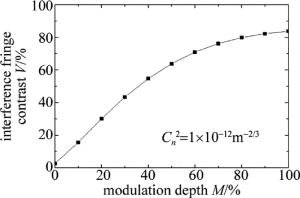
Figure 4. Relationship between dual-frequency laser signal modulation index and interference fringe contrast
从图 4可以看出，在大气湍流干扰的情况下，随着双频激光调制深度的增大，干涉条纹的对比度增加，说明其抗大气湍流干扰能力增强。
-
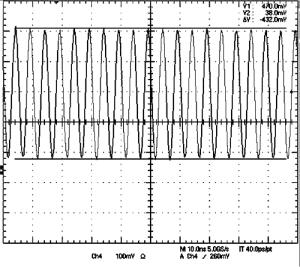
采用图 1所示的实验系统进行实验，使用图 2中模拟的大气湍流相位屏(Cn2=1×10-12m-2/3)作为空间光调制器的输入，双频激光的调制深度通过调节两路光功率及偏振控制器来改变。采用光电探测器接收双频激光，示波器显示的拍频信号波形图包含直流分量，如图 5所示。由波形图包络的最大值Y1与最小值Y2，对应调制深度的计算公式：
Figure 5. Oscilloscope waveform when measuring modulation index
$ M = \frac{{{I_{\max }} - {I_{\min }}}}{{{I_{\max }} + {I_{\min }}}} = \frac{{{Y_1} - {Y_2}}}{{{Y_1} + {Y_2}}} $
(17) 由图 5中所示数据，可得此时双频激光的调制深度为M=(470-38)/(470+38)×100%=85.04%。
SLM在未输入控制信号时相当于普通的反射镜，因此在不同的调制深度下，双频激光这一路的干涉光可以在有无大气湍流干扰时分别与单频激光进行干涉，用CCD拍摄干涉板上的干涉条纹图形，对图像进行处理得到条纹对比度。通过条纹对比度的变化可以判断双频激光信号的相位受大气干扰的程度，进而判断其抗大气干扰的能力。
-
采用MATLAB软件进行图像处理。由于实验中获得的干涉图样背景光噪声较多，首先将所获得的图像(JPG格式文件)转换为灰度图像，利用imsubtract函数将初始干涉图像中的背景光信号剔除。为消除镜面干涉等噪声干扰，分别遮挡干涉的两路光路，获得单频和双频激光的噪声干扰图像，进行去除背景光噪声操作。然后从已消除背景光噪声的干涉图样中减去两路镜面干扰图像，接着用imfilter函数消除其它噪声的干扰，并调用improfile函数获得光强分布信息，最后计算条纹对比度。
以调制深度为85%且未加大气湍流的实验图像为例，介绍图像处理过程。
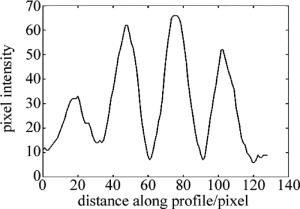
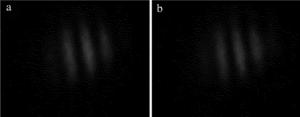
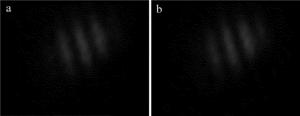
图 6a和图 6b分别是单路光在镜面上的散射噪声信号，图 6c是两路光干涉图形，图 6d是将干涉图形减去两路光噪声后的干涉图形。可以看出，做了降噪处理后条纹的对比度得到加强。图 7是由图 6d中的条纹计算出来的强度分布的曲线。其中横坐标是沿指定路径的像素点，纵坐标是对应像素点强度值，由此可以计算得条纹对比度为V=(213-34)/(213+34)×100%=72.47%。
Figure 6. Interference image with modulation index of 85% and without atmospheric turbulence
Figure 7. Light intensity distribution curve of interference image
-
实验中分别测量了双频激光调制深度在26.32%, 42.04%, 67.59%和85.04%这4种情况下，未加和加入大气湍流影响时的条纹对比度，处理后的干涉图像分别如图 8、图 9、图 10和图 11所示。计算得到4种情况下干涉条纹对比度，计算结果列于表 1中。
Figure 8. Interference image with modulation index of 26.32%
Figure 9. Interference image with modulation index of 42.04%
Figure 10. Interference image with modulation index of 67.59%
Figure 11. Interference image with modulation index of 85.04%
Table 1. Interference fringe contrasts at different modulation depths and their changes
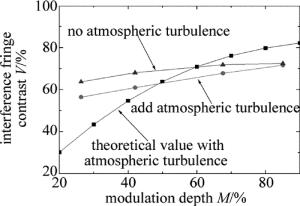
modulation index M interference fringe contrast without atmospheric turbulence V1 interference fringe contrast with atmospheric turbulence V2 change of interference fringe contrastΔ=V1-V2 26.32% 63.72% 56.41% 7.31% 42.04% 68.06% 60.96% 7.10% 67.59% 71.87% 67.78% 4.09% 85.04% 72.47% 71.65% 0.82% 在实验时确保了相同调制深度下，加大气湍流前后的实验条件和环境不变，从而保证实验的准确性。从表 1和图 12可以看出，同样调制深度时，未加大气湍流比加入大气湍流的条纹对比度高，随着调制深度增加，干涉条纹对比度都增加，但是两者的差距越来越小，说明随着调制深度的增加，大气湍流的影响逐渐减小。由于理论推导时，未考虑各光路初始相位、偏振态以及其它噪声等情况，所以理论值与实验值略有偏差，但是变化规律是一致的。从表 1和图 12可以看出，调制深度越大，大气湍流造成的条纹对比度的变化越小，即随着调制深度增大，大气湍流的影响越小，说明深度调制的光载微波具有更强的抗大气干扰能力。
Figure 12. Relationship between modulation depth and interference fringe contrast in experiment and theory under strong atmospheric turbulence
-
为研究双频激光的调制深度与其抗大气干扰能力的关系，首先建立了相应的理论模型，得出双频激光的调制深度与干涉条纹对比度的关系。并搭建了Mach-Zehnder干涉仪，以双频信号为光源，利用干涉条纹的对比度变化表征大气湍流对双频激光造成的扰动。改变双频激光的调制深度，分别在26.32%, 42.04%, 67.59%和85.04% 4种调制深度下，比较有无大气湍流时干涉条纹的对比度的变化，利用CCD采集干涉图像并用MATLAB进行图像处理获得干涉条纹对比度。实验结果表明，双频信号的调制度越深，其抗大气湍流干扰的能力越强，该结论对双频激光雷达光源的选择具有一定的参考意义。
光载微波信号抗大气干扰的研究
Study on anti-atmospheric turbulence interference of light borne microwave signal
-
摘要: 为了研究射频强度调制激光信号光源的参量，特别是调制深度对调制波的抗干扰能力产生的影响，采用干涉法对射频强度调制激光信号在通过大气湍流干扰后其相位的变化进行了理论分析和实验验证。搭建了Mach-Zehnder干涉仪，参加干涉的两束光分别为未经调制的单频光和调制后的双频光。以干涉条纹对比度作为信号相位起伏的衡量标准，比较不同大气湍流干扰条件下，干涉条纹的对比度随调制深度的变化。大气湍流由空间光调制器模拟产生，分别在26.32%，42.04%，67.59%和85.04% 4种调制深度下，比较有无大气湍流时干涉条纹的对比度的变化。结果表明，调制信号的调制度越深，其抗大气湍流干扰的能力越强。该结论对双频激光雷达光源的选择具有一定的参考意义。Abstract: In order to study effect of parameters of radio frequency(RF) intensity modulation laser signal sources, especially modulation index, on anti-atmospheric turbulence interference, phase change of the RF intensity modulation laser signal passing through atmospheric turbulence was analyzed theoretically and verified experimentally. A Mach-Zehnder interferometer was built, and two interference beams were single frequency light without modulation and dual frequency light with modulation respectively. The contrast of interference fringes was taken as the criterion of signal phase fluctuation. The contrast of interference fringes with the change of modulation depth were compared under different atmospheric turbulence conditions.The atmospheric turbulence was generated by the simulation of spatial light modulator. The contrast of interference fringes with and without atmospheric turbulence was compared under four modulation depths of 26.32%, 42.04%, 67.59% and 85.04%, respectively. The results show that, the deeper the modulation level of modulation signal is, the stronger its ability to resist atmospheric turbulence is. The conclusion has some reference significance for the selection of dual frequency lidar light sources.
-
Key words:
- physical optics /
- modulation index /
- interference /
- atmospheric turbulence /
- fringe contrast
-
Figure 1. System structure of anti-atmospheric interference experiment with dual frequency laser
Figure 3. Interference fringes under strong atmospheric turbulence with diffe-rent modulation depths
Figure 4. Relationship between dual-frequency laser signal modulation index and interference fringe contrast
Figure 6. Interference image with modulation index of 85% and without atmospheric turbulence
a—of the single frequency optical signal at the mirror b—of the dual-frequency signal at the mirror c—of the two beams d—after subtracting the noises
Figure 8. Interference image with modulation index of 26.32%
a—without atmospheric turbulence b—with atmosphere
Figure 9. Interference image with modulation index of 42.04%
a—without atmospheric turbulence b—with atmosphere
Figure 10. Interference image with modulation index of 67.59%
a—without atmospheric turbulence b—with atmosphere
Figure 11. Interference image with modulation index of 85.04%
a—without atmospheric turbulence b—with atmosphere
Figure 12. Relationship between modulation depth and interference fringe contrast in experiment and theory under strong atmospheric turbulence
Table 1. Interference fringe contrasts at different modulation depths and their changes
modulation index M interference fringe contrast without atmospheric turbulence V1 interference fringe contrast with atmospheric turbulence V2 change of interference fringe contrastΔ=V1-V2 26.32% 63.72% 56.41% 7.31% 42.04% 68.06% 60.96% 7.10% 67.59% 71.87% 67.78% 4.09% 85.04% 72.47% 71.65% 0.82% 
下载: 导出CSV
-
[1] COCHENOUR B, MULLEN L, MUTH J. A modulated pulse laser for underwater detection, ranging, imaging, and communications[J]. Proceedings of the SPIE, 2012, 8372:83720S. doi: 10.1117/12.918711 [2] MULLEN L J, VIEIRA A J C, HEREZFELD P R, et al. Application of RADAR technology to aerial LIDAR systems for enhancement of shallow underwater target detection[J]. IEEE Transactions on Microwave Theory & Techniques, 1995, 43(9):2370-2377. [3] ILLIG D W, LEE R W, MULLEN L J. FMCW optical ranging technique in turbid waters[J].Proceedings of the SPIE, 2015, 9459:94590B. [4] YI F, OU F, LIU B Y, et al. Electro-optic modulator with exceptional power-size performance enabled by transparent conducting electrodes[J]. Optics Express, 2010, 18(7):6779-6796. doi: 10.1364/OE.18.006779 [5] AHMAD H, AMIRI I S, SOLTANIAN M R K, et al. Dual-wavelength erbium-doped fiber laser to generate terahertz radiation using photonic crystal fiber[J]. Journal of Lightwave Technology, 2015, 33(24):5038-5046. doi: 10.1109/JLT.2015.2495255 [6] ROLLAND A, FREIN V, VALLET M, et al. 40GHz photonic synthesizer using a dual-polarization microlaser[J]. IEEE Photonics Technology Letters, 2010, 22(23):1738-1740. doi: 10.1109/LPT.2010.2084077 [7] JUAN Y S, LIN F Y. Photonic generation of broadly tunable microwave signals utilizing a dual-beam optically injected semiconductor laser[J]. IEEE Photonics Journal, 2011, 3(4):644-650. doi: 10.1109/JPHOT.2011.2158413 [8] HAMEL C, BONDU F, LOAS G, et al. Dual frequency laser with two continuously and widely tunable frequencies for optical referencing of GHz to THz beatnotes[J]. Optics Express, 2014, 22(15):17673-17678. doi: 10.1364/OE.22.017673 [9] GILLES H, THÉVENIN J, BRUNEL M, et al. Beat-note locking in dual-polarization lasers submitted to frequency-shifted, optical feedback[J]. Journal of the Optical Society of America, 2011, B28(5):1104-1110. [10] KANG Y, YANG S, BRUNEL M, et al. Second-harmonic generation of a dual-frequency laser in a MgO:PPLN crystal[J]. Applied Optics, 2017, 56(11):2968-2972. doi: 10.1364/AO.56.002968 [11] ZHENG Zh, ZHAO Ch M, ZHANG H Y, et al. Phase noise reduction by using dual-frequency laser in coherent detection[J]. Optics & Laser Technology, 2016, 80:169-175. [12] XIANG J S. High-frequency error compensation method for the fast fourier transform-based turbulent phase screen[J]. Acta Optica Sinica, 2014, 34(10):1001003(in Chinese). doi: 10.3788/AOS [13] BEGHI A, MASIERO A, CENEDESE A. Multiscale stochastic approach for phase screens synthesis[J]. Applied Optics, 2011, 50(21):4124-33. doi: 10.1364/AO.50.004124 [14] FENG F, LI Ch W. Simulation of atmospheric turbulence phase screen based on wavelet analysis[J]. Acta Optica Sinica, 2017, 37(1):0101004(in Chinese). doi: 10.3788/AOS [15] NIU H H, HAN Y P. Performance analysis of Bessel-Gaussian vortex beam's propagation in atmospheric turbulence[J]. Laser Technology, 2017, 41(3):451-455(in Chinese). -
点击查看大图
计量
- 文章访问数: 8212
- HTML全文浏览量: 5895
- PDF下载量: 114
- 被引次数: 0
