网站地图
下载:
-
相干合成是一种获得高质量、高功率激光输出的有效方案[1]，已成为国内外激光领域的研究热点。目前常见的相干合成方案中，大都采用阵列排布结构，由于占空比的问题，导致相干合成中能量向旁瓣分散[2-7]，降低了能量集中度。而相干偏振合成技术方案弥补了大规模阵列排布方式的缺陷，在多链路、高功率拓展的同时实现了共孔径输出[8-9]，且具有极高的理论合成效率。基于该方案，国内外研究机构进行了一些相关的实验研究，都获得了较为理想的实验效果。2010年，美国洛克希德·马丁技术公司利用光纤主振荡功率放大系统实现了4路瓦级光纤激光的相干偏振合成，获得了25W的激光输出，光束质量接近衍射极限，合成效率达到94%[8]。新加坡国防科技研究院进行了Nd: YVO4板条激光器的双光束相干偏振合成，合成效率高达99%[10]。2013年，德国弗里德里希·席勒大学进行了4路飞秒脉冲激光的相干偏振合成实验，实现了530W激光平均功率输出，合成效率达到93%[11]。2016年，国防科技大学进行了4路500W级保偏放大器的偏振相干合成，输出功率高达2164W，合成效率达到94.5%[12]。在相干偏振合成向更多链路拓展时，器件本身的损耗、偏振误差、同轴性调节、动态锁相残差、高功率下的退偏等因素都是难以完全避免的，从而使得合成效率会逐级降低。要控制参与合成的所有光束的偏振方向达到完全相同，在技术上存在一定难度，对光束功率、功率密度、光束质量的研究较多[13-15]，但研究偏振误差对相干偏振合成效率的影响及系统光路拓展性的文献报道较少。
本文中以两基模高斯光束相干合成建立物理模型，利用矩阵实验室MATLAB仿真软件，数值模拟和分析了偏振误差、偏振合束器(polarization beam combiner，PBC)损耗、半波片(half wave-plate，HWP)损耗对相干偏振合成效率的影响，以及不同结构的可扩展性。
-
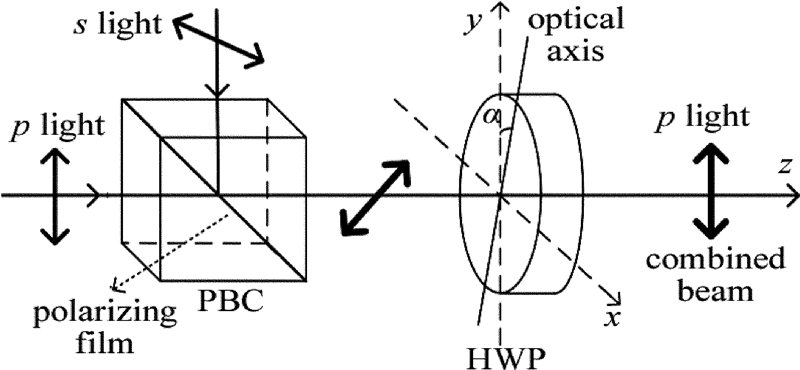
图 1中给出了相干偏振合成的基本光路结构。图中α是HWP光轴和y轴之间的夹角。具有相同频率并且偏振方向相互正交的线偏振光(p光和s光)，当它们的相位差锁定为π的整数倍时，通过偏振合束器合成为一束偏振光，再通过半波片调整其偏振态成为p光(或者s光)后，可进行下一级的合成。参与合成的两光场为：
$ {E_1}(x,y,{\beta _1}) = {A_1}({\beta _1}){\rm{exp}}[({x^2} + {y^2})/{w^2}] $
(1) $ {E_2}(x,y,{\beta _2},\delta ) = {A_2}({\beta _2}){\rm{exp}}\left[ {\frac{{ - ({x^2} + {y^2}){\rm{ }}}}{{{w^2}}}} \right]{\rm{exp}}({\rm{i}}\delta ) $
(2) 
Figure 1. Principle of polarized beam combination
式中，A1(β1)=A1cosβ1，A2(β2)=A2cosβ2，w为束腰半径，δ为两光束的相位差，A1和A2分别为两光束的振幅, β1和β2分别为两入射光束的偏振误差。
令δ=kπ(k为整数)，两光束合成后在y轴方向的光强Ⅰ和光功率P分别为:
$ I = {[{E_1}{\rm{cos}}\left( {\pi /4} \right) + {E_2}{\rm{sin}}\left( {\pi /4} \right)\left] \cdot \right[{E_1}{\rm{cos}}\left( {\pi /4} \right) + {E_2}{\rm{sin}}\left( {\pi /4} \right)]^*} $
(3) $ P = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {I{\rm{d}}x{\rm{d}}y} } $
(4) 式中，上标符号*表示共轭复数。两光束存在偏振误差就会引起不同的合成光功率。
考虑到参与合成的两光束输入总功率P0为：
$ {P_0} = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {({E_1}^2 + {E_2}^2){\rm{d}}x{\rm{d}}y} } $
(5) 则可以定义一个单元的相干偏振合成效率ηc为：
$ {\eta _c} = P/{P_0} $
(6) 从推导过程可知，在其它参量不变时，两光束如果存在偏振误差就会引起合成效率的变化。
-
由于单路激光的功率有限，通过系统拓展可以实现多路激光的相干合成，进而获得高功率。根据偏振合成的光路结构，光路拓展采用的方案如图 2所示。
Figure 2. Schematic diagram of coherent polarization beam combining
图 2是几种主要拓展结构的光路示意图。Y型结构的特点是每一级参与合成的光束光强都相等，R型结构的特点是合成光强呈Z字形走向，F型结构的特点是光路最简单，可以通过线性级联的方式实现拓展。在结构拓展时，如果光束数目是N，整个系统至少需要N－1个PBC，2(N－1)个HWP，考虑到光能量在这两个元件中产生的损耗，Y型，R型，F型3种结构拓展后整个系统的合成效率分别为：
$ \left\{ \begin{array}{l} {\eta _{\rm{Y}}} = {\eta _{\rm{c}}}^m{\rm{ }}\left[ {\frac{{{T_{{\rm{HWP}}}}({R_{{\rm{PBC}}}} + {T_{{\rm{PBC}}}}){\rm{ }}}}{2}} \right]{^m},(m = {\rm{lo}}{{\rm{g}}_2}N){\rm{ }}\\ {\eta _{\rm{R}}} = [ - {T_{{\rm{HWP}}}}^N{\eta _{\rm{c}}}^N{R_{{\rm{PBC}}}}^{}N + (1 - {T_{{\rm{HWP}}}}{\eta _{\rm{c}}}{T_{{\rm{PBC}}}}){T_{{\rm{HWP}}}}^{N - 1} \times \\ {\rm{ }}{\eta _{\rm{c}}}^{N - 1}{R_{{\rm{PBC}}}}^{N - 1} + {T_{{\rm{HWP}}}}{\eta _{\rm{c}}}{T_{{\rm{PBC}}}}]/[N(1 - {T_{{\rm{HWP}}}}{\eta _{\rm{c}}}{R_{{\rm{PBC}}}})]\\ {\eta _{\rm{F}}} = [ - {T_{{\rm{HWP}}}}^N{\eta _{\rm{c}}}^N{T_{{\rm{PBC}}}}^N + (1 - {T_{{\rm{HWP}}}}{\eta _{\rm{c}}}{R_{{\rm{PBC}}}}){T_{{\rm{HWP}}}}^{N - 1} \times \\ {\rm{ }}{\eta _{\rm{c}}}^{N - 1}{T_{{\rm{PBC}}}}^{N - 1} + {T_{{\rm{HWP}}}}{\eta _{\rm{c}}}{T_{{\rm{PBC}}}}]/[N(1 - {T_{{\rm{HWP}}}}{\eta _{\rm{c}}}{R_{{\rm{PBC}}}})] \end{array} \right. $
(7) 式中，ηc为单元合成效率，RPBC和TPBC分别为PBC对光束的反射率和透射率，THWP为HWP对光束的透射率，N为光束数目。
-
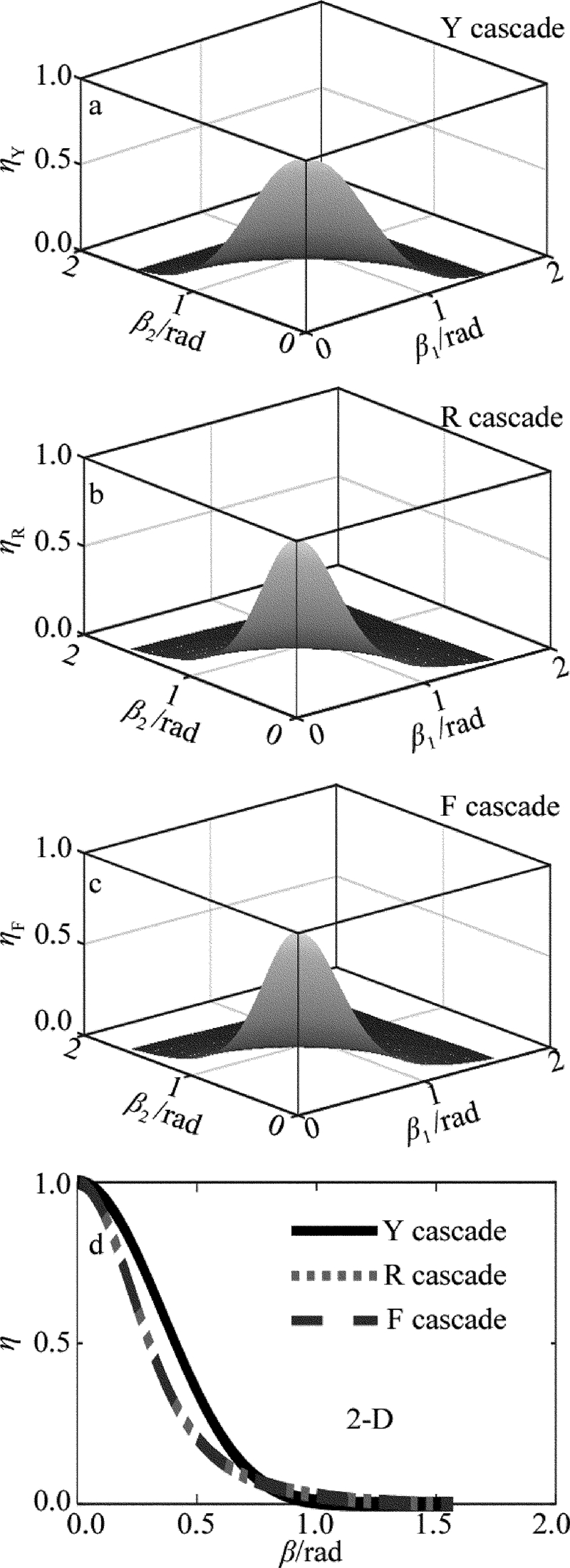
下面分析偏振误差对3种结构合成效率的影响，忽略PBC和HWP损耗时，计算参量如下：HWP的透射率THWP=100%，PBC的反射率RPBC=100%，PBC的透射率TPBC=100%，光束数目N=16，相位差δ=0，偏振误差对3种结构合成效率的影响如图 3所示。
Figure 3. Influence of polarization error on combining efficiency of three structures without PBC and HWP loss
从图 3计算结果可以得知，3种结构的合成效率都会随偏振误差的增大而减小，相对而言Y型结构对偏振误差的容差能力最高。当β1=β2=0.03rad时，Y型、R型、F型3种结构的合成效率分别为99.64%，99.24%，99.24%;偏振误差仅增加0.03rad，Y型、R型、F型3种结构的合成效率分别下降了0.36%，0.76%，0.76%。为了保证系统的合成效率高于99%，Y型、R型、F型结构的偏振误差必须分别小于0.0502rad，0.0346rad，0.0346rad，以上结果表明, 偏振误差是影响相干偏振合成效率的一个重要因素。图 3中R型、F型合成效率曲线相同的原因是两种结构具有相同的光路合成结构，均为反射加透射式，在PBC的折射率和反射率均为100%时，效率是相同的。
实际情况下，PBC和HWP对光能量会产生损耗，商品化的PBC反射率和透射率器件可以分别达到99.5%，96%以上，而HWP的透射率可以达到99.7%以上。选取一般产品参量后，计算参量如下：HWP透射率THWP=99.7%，PBC反射率RPBC=99.5%，PBC透射率TPBC=96%，光束数目N=16，相位差δ=0，偏振误差对3种结构合成效率的影响如图 4所示。
Figure 4. Influence of polarization error on combining efficiency of three structures with PBC and HWP loss
由图 4可以得到，考虑到两个关键元件导致的光能量损耗后，3种结构的合成效率相比图 3有了更明显的变化。同样Y型结构对偏振误差的容差能力最高，而R型较之F型容差性能略好。当偏振误差为0rad时，Y型、R型、F型3种结构的最大效率分别为90.21%，90.43%，72.90%，这表明由PBC和HWP导致的光损耗也会引起合成效率下降。
当偏振误差为0.03rad时，Y型、R型、F型3种结构的合成效率分别为89.88%，89.75%，72.41%，可见合成效率分别下降了0.33%，0.68%，0.49%。对于Y型结构，要保证90%以上的合成效率，16级合成系统必须将偏振误差控制在0.0238rad以内。图 4d中R型、F型合成效率存在差别，原因是PBC的反射率大于其透射率。R型结构是前级合成光强经PBC反射，待合成光强经PBC透射，F型结构是前级合成光强经PBC透射，待合成光强经PBC反射，前级合成光强大于待合成光强，因此R型结构合成效率大于F型合成效率。
-
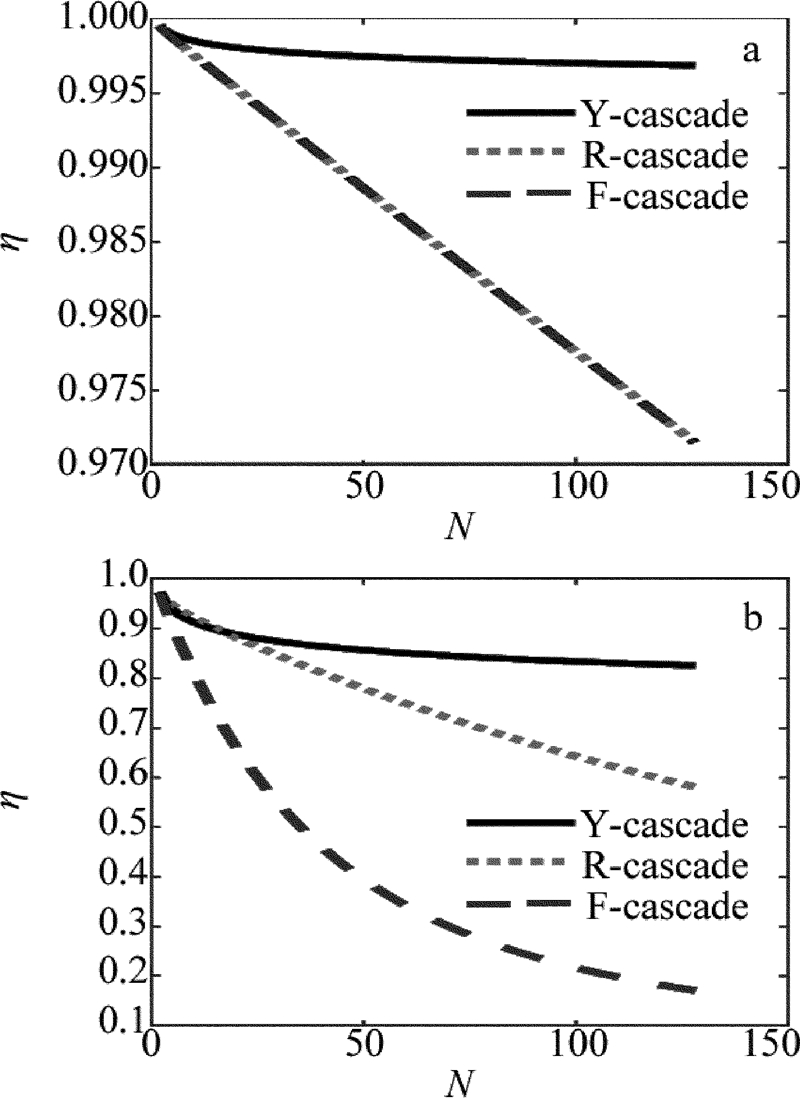
如果要进一步提高参与合成的光束数量，需要进一步分析在偏振误差影响下3种结构的拓展性。如果忽略PBC和HWP损耗时，取RPBC=THWP=TPBC=100%，δ=0，β1=β2=0.03rad。当考虑PBC和HWP损耗时，取RPBC=99.5%，TPBC=96%，THWP=99.7%，δ=0，β1=β2=0.03rad，拓展计算结果如图所5所示。
Figure 5. Extensibility of three kinds of structuresunder the influence of polarization error a—ignore loss of PBC and HWP b—consider loss of PBC and HWP
由图 5可以看出，忽略PBC和HWP损耗时，当系统拓展至128路，Y型、R型、F型结构的合成效率分别为99.39%，97.15%，97.15%，Y型结构的合成效率最高。考虑PBC和HWP损耗时，在相同偏振误差情况下，系统拓展至128路，Y型、R型、F型3种结构的合成效率分别为83.24%，58.67%，17.82%。由此可知，Y型结构具有最好的光束拓展性能。
-
为进一步提高偏振合成系统的效率，研究了偏振误差对多级合成效率的影响。计算了不同条件下Y型、R型、F型3种不同偏振合成结构的合成效率。无论是否考虑偏振合束器与半波片对光的吸收损耗，随着两束线偏光偏振方向控制误差的增大，偏振合成效率都会逐渐降低。相比较而言，能量分布更为均匀的Y型结构对偏振误差具有最好的容差特性，也具有最好的拓展能力。定量计算的结果表明，当偏振合束器的透过率和反射率分别为96%与99.5%、半波片的透过率为99.7%时，如果偏振误差增大到0.03rad，一个Y型16路合成系统的合成效率将下降为89.88%。如果要确保系统的合成效率高于90%，该结构的偏振误差必须控制在0.0238rad以内。当参与合成的光束增加到128路，此时0.03rad的偏振误差将导致Y型结构的合成效率降为83%左右。
偏振误差对相干偏振合成效率的影响
Effect of polarization error on combining efficiency of coherent polarization beam
-
摘要: 为了进一步提高相干偏振合成的效率，采用数值模拟方式，对偏振误差的影响及系统的拓展性进行了分析，并计算了偏振误差在3种不同拓展结构下对相干偏振合成效率的影响。当偏振合束器的透过率和反射率分别是96%和99.5%、半波片的透过率是99.7%时，Y型结构16路光束的整体合成效率会在偏振误差增大到0.03rad时下降0.33%；随着合成路数的增大，合成效率逐渐降低，当光束拓展至128路时，Y型结构的合成效率将下降至83%。结果表明，光功率相对平衡的Y型结构具有最高的合成效率，同时受偏振误差的影响最小。该研究确定了系统的最佳合成方案，为基于相干偏振合成的效率分析提供了参考。Abstract: To further improve combining efficiency of polarized beam combination, effect of polarization error and systematical extensibility were analyzed byusing numerical simulation method. The influence of polarization error on combining efficiency of coherent polarization beams was calculated under three kinds of different expanded structures. The overall combining efficiency of 16 path beamswith Y structure decreases 0.33% when the transmittance of polarization beam combiner(PBC) and the reflectance of PBC are 96% and 99.5% respectively, the transmittance of the half wave-plate is 99.7% and polarization error is 0.03rad. The combining efficiency declines gradually with the increase of beam number.The combining efficiency of 128 beams with Y structure drops to 83%. The results show that, Y structure with the relative balance of light power has the highest combining efficiency, and has the least influence by the polarization error.This study determines the optimal combining scheme of the system and provides a reference for the efficiency analysis based on coherent polarization combination.
-
Key words:
- laser technique /
- combining efficiency /
- polarization combination /
- polarization error
-
Figure 2. Schematic diagram of coherent polarization beam combining
a—principle of Y-cascade structure b—principle of R-cascade structure c—principle of F-cascade structure
Figure 3. Influence of polarization error on combining efficiency of three structures without PBC and HWP loss
Figure 4. Influence of polarization error on combining efficiency of three structures with PBC and HWP loss
-
[1] YU C X, AUGST S J, REDMOND S M, et al. Coherent combining of a 4kW, eight-element fiberamplifier array[J]. Optics Letters, 2011, 36(14):2686-2688. doi: 10.1364/OL.36.002686 [2] ZHOU J, TANG X J, CHEN S B, et al. Influence of system deviation on laser coherent combination[J]. Laser & Infrared, 2015, 45(4):378-382(in Chinese). [3] LI F D, GUO H N, SUN J G, et al. Simulation and experimental study on coherentcombinationof dual beam fiber laser[J]. Laser Technology, 2014, 38(4):509-514(in Chinese). [4] JIANG, M H, SU Y, LU F, et al. Influence of polarization on laser beam coherent combining[J].High Power Laser and Particle Beams, 2013, 25(3):611-614(in Chinese). doi: 10.3788/HPLPB [5] SHI X G, DOU R H, JING Sh, et al. Influence of system jitter on far field of coherently combined beam[J]. Laser Technology, 2009, 33(5):493-496(in Chinese). [6] JIANG M H, SU Y, LU F, et al. Influence of duty ratio on laser beam coherent combining[J]. Laser & Infrared, 2012, 42(10):1103-1106(in Chinese). [7] LI B, LIU Y, ZENG Sh G, et al. Study on coherent beam combination of fiber laser array[J].Laser Technology, 2015, 39(5):712-716(in Chinese). [8] UBERNA R, BRATCHER A, TIEMANN B G. Power scaling of a fiber master oscillator power amplifier system using a coherent polarization beam combination[J]. Applied Optics, 2010, 49(35):6762-6765. doi: 10.1364/AO.49.006762 [9] UBERNA R, BRATCHER A, TIEMANN B G. Coherent polarization beam combination[J]. IEEE Journal of Quantum Electronics, 2010, 46(8):1191-1196. doi: 10.1109/JQE.2010.2044976 [10] PHUA P B, LIM Y L. Coherent polarization locking with near-perfect combining efficiency[J]. Optics Letters, 2006, 31(14):2148-2150. doi: 10.1364/OL.31.002148 [11] KLENKE A, BREITKOPF S, KIENEL M, et al. 530W, 1.3mJ, four-channel coherently combined femtosecond fiber chirped-pulse amplification system[J]. Optics Letters, 2013, 38(13):2283-2285. [12] MA P F, WANG X L. Coherent polarization beam combining of fiber lasers to 2kW power-level[J]. High Power Laser and Particle Beams, 2016, 28(4):4-5(in Chinese). [13] CAO F L, ZHANG R Zh. Effects of system errors on coherent polarization beam combining efficiency[J]. High Power Laser and Particle Beams, 2015, 27(6):96-101(in Chinese). [14] DONG H C, LIU Y, YI K, et al. Theory analysis of polarized coherent combination. Chinese Journal of Lasers, 2009, 36(9):2346-2351(in Chinese). doi: 10.3788/JCL [15] LU Ch Y, LIU X, LIU Y, et al. Coherent combining of two beams based on polarization phase locking[J]. Chinese Journal of Lasers, 2009, 36(6):1437-1441(in Chinese). doi: 10.3788/JCL -
点击查看大图
图(5)
计量
- 文章访问数: 4787
- HTML全文浏览量: 3082
- PDF下载量: 145
- 被引次数: 0
