网站地图
下载:
-
利用激光冷却原子的思想由美国科学家HANSCH和SCHAWLOW于1975年首次提出[1]，由此发展而来的激光冷却技术被广泛地应用于超精细光谱[2]、玻色爱因斯坦凝聚[3]、超冷原子碰撞[4-5]、量子频率标准[6]、原子光刻[7]等科学研究和技术领域。激光冷却原子就是要降低原子的温度，热力学理论解释为压窄原子系综的速度分布范围，利用共振或近共振激光宏观上的机械作用力效应来实现[8-9]。当一束负失谐于原子共振频率的激光与原子相向传播，由于多普勒效应，原子感受到的激光频率增大，当辐射场的散射力频率满足ω=ωa- k · v (其中，k为激光的波矢，大小是以2π为单位的波数，ω为激光频率，ωa为原子辐射跃迁频率，v为原子运动速度)时，即原子接收到的激光频率与原子共振频率相等，光对原子的这种共振散射力(也称为耗散力)可使原子不断减速，达到冷却的目的。俄罗斯科学家BALYKIN等人[10]于1979年首先利用激光扫描方法实现原子减速，激光扫描法可覆盖从减速起始至零速率的全部多普勒频率范围，使大量原子减速，从而解决了由于原子不断被减速而导致激光频率脱离原子共振频率的问题。基于激光冷却技术人们对碱金属原子的冷却进行了研究，1985年, ZHU研究小组利用3对互相垂直的激光束冷却钠原子[11]，即3维原子冷却(称为“光学粘团”)，原子速度由1cm/20ms降低到1cm/1s，原子温度被冷却至240μK。近年来, 以碱土金属原子为对象的激光冷却得到世界范围内许多研究小组的青睐[12-14]，大部分碱土金属原子基态核自旋为零，无磁子能级存在，因此对于基态1S0~ 1P1的冷却为标准多普勒冷却。在这类原子中尤以锶原子为研究焦点，锶原子1S1~1P1跃迁辐射速率强且为近似封闭循环，能实现高效的多普勒冷却。意大利科学家TINO等人从实验上研究了碱土金属锶原子的冷却属性[15]，通过磁光阱冷却与俘获得到温度仅为几个毫升的冷锶原子。美国莱斯大学研究小组[16]利用激光冷却技术也实验实现了中性锶原子的冷却，并以此冷锶原子样品为基础，研究了锶原子5s5p3P2~5s4d3D2跃迁对冷却效果的影响。中国计量科学研究院[17]在研制以锶原子为对象的高精度时间频率基准中，进行了冷锶原子样品的实验制备并实现其温度为2mK~3mK。对于碱土金属锶原子的研究，目前大多集中于实验上，通过实验手段获取满足研究需求的冷原子样品。
本文中从理论上对碱土金属锶原子的激光多普勒冷却进行分析，研究锶原子在多普勒冷却光场中的特性。从Heisenberg方程出发，对原子在光场中的受力情况进行分析研究。基于中性锶原子的冷却循环跃迁(5s2)1S0~(5s5p)1P1，在1维冷却激光场和3维磁光阱两种条件下，分析了锶原子的受力情况以及激光强度、频率失谐等参量对锶原子所受耗散力特性及原子温度等的影响。
-
基于Heisenberg方程以及布洛赫方程稳态处理方法[18]，处于近共振激光场中的原子受到的力由两部分组成：
$ \mathit{\boldsymbol{F}}{\rm{ }} = {\rm{ }}\mathit{\boldsymbol{F}}{_{\rm{d}}} + {\rm{ }}\mathit{\boldsymbol{F}}{_{\rm{r}}} $
(1) 式中，Fd为耗散力，它与光场的相位有关；Fr为偶极力，与光场的振幅梯度有关。
处于近共振光场中的原子，当原子吸收一个光子后跃迁至激发态，其动量p将会改变ħk，其中ħ为约化普朗克常数。经过一定时间后通过自发辐射重返基态，发出光子各方向等概率。动量损失在统计平均上为零，但吸收光子引起的原子动量变化则得到累积，定向的有积累效应的光子吸收和大量无规则的光子发射的统一则产生耗散力，即一个多次吸收光子动量和发射光子动量过程的平均。
在激光场为平面波的情况下，原子所受耗散力为:
$ \mathit{\boldsymbol{F}}{_{\rm{d}}} = ħ\mathit{\boldsymbol{k \boldsymbol{\varGamma} }}\frac{{{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^2}/4}}{{{\delta ^2} + \left( {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^2}/4} \right) + ({\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^2}/2)}}{\rm{ }} $
(2) 式中, Γ为能级跃迁速率，Ω为拉比频率，δ为激光频率相对原子共振跃迁频率的失谐量。由于Fd=pWab，Wab为原子能级系统上下能级a, b的稳态跃迁概率，即单位时间内原子吸收的光子数。Fd=ħk Wab，其中为跃迁能级的饱和参量，Ⅰ为激光光场强度，Ⅰs为能级饱和光强。激光强度越大即意味着饱和参量数值越大。在饱和参量值s较小时，原子跃迁概率与激光强度成正比，但当激光场光强增大时，饱和参量时，跃迁概率达到饱和Γ/2，即表示原子跃迁过程中有一半时间处于激发态。
对于锶原子基于(5s2)1S0~(5s5p)1P1跃迁能级的多普勒冷却，其跃迁自发辐射速率Γ1S0→1P1=2×108s-1，自然辐射线宽为32MHz。锶原子所受耗散力最大值Fmax=ħkΓ/2，对应的最大加速度amax=(ħ-k/m)× Γ/2，m为原子质量。对于锶原子其质量为1.44×10-25kg。在波长λ=461nm的激光场共振作用下，对于每一次吸收-辐射光子的循环，原子速度的每一次改变等量于反冲速度的改变，其变化量级为10-2m/s。虽然变化量很小但由于辐射速率很高(自然辐射速率的一半约等于108/s)，因此它可以被累计至一个很大的数目，其加速度的数量级约等于105g，g为重力加速度。可见作用于原子的这种激光共振力的数值是非常大的，因此在耗散力的作用下处于461nm共振光场中的锶原子，其速度会发生明显改变。
-
当速度为v的原子与一束频率负失谐于原子共振频率的激光(即红移激光)相向运动时，即原子处于1维行波场，原子所受到的耗散力可表达为：
$ {\mathit{\boldsymbol{F}}_{\rm{d}}} = ħ\mathit{\boldsymbol{k \boldsymbol{\varGamma} }}\frac{{{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^2}/4}}{{{{({\omega _{\rm{l}}} - {\omega _{\rm{a}}} + {\rm{ }}\mathit{\boldsymbol{k}}{\rm{ }}\cdot{\rm{ }}\mathit{\boldsymbol{v }})}^2} + ({\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^2}/4) + ({\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^2}/2)}}{\rm{ }} $
(3) 式中, ω1为激光角频率，ωa为原子辐射跃迁频率，即角频率。
在1维驻波激光光场中，两束激光相向传播垂直照射运动原子，原子受到的耗散力为：
$ \mathit{\boldsymbol{F}}{_{\rm{d}}} = ħ\mathit{\boldsymbol{k}}\frac{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}}{2}\left\{ {\frac{s}{{1 + s + {{[2(\delta - \mathit{\boldsymbol{k}}\cdot\mathit{\boldsymbol{v}})/\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}]}^2}}} - \frac{s}{{1 + s + {{[2(\delta + \mathit{\boldsymbol{k}}\cdot\mathit{\boldsymbol{v}})/\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}]}^2}}}} \right\} $
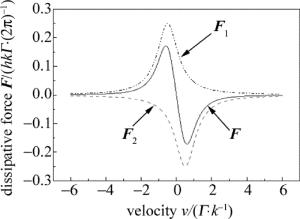
(4) 当原子处于低激光强度的共振光场，即弱光场条件下，由(4)式可推导出阻尼系数的大小α=-8ħk2δ×(s/Γ)/[1+(2δ/Γ)2]2。首先分析得到1维驻波激光场中原子所受耗散力与原子运动速度的关系, 如图 1所示。图中两条虚线为原子受到的单束激光耗散力F 1和F 2，实线为两束对射红移激光的耗散合力F，即驻波场耗散力。由于原子具有一定范围的速度分布，在负失谐的激光场中，若原子速度太快则由于多普勒频移过大使得无法共振，不能被冷却；若速度太慢则总是脱离共振。多普勒冷却机制对速度在|v| < δ/k范围内的原子冷却最有效，多普勒冷却的结果使原子很宽的速度分布被压窄，并被移到了低速区。
Figure 1. Relationship between dissipative force of 1-D laser standing wave and atomic velocity
基于1维驻波激光光场的耗散力，接下来对耗散力相关的阻尼系数进行分析，图 2为激光光场的强度(即饱和参量s)及频率失谐δ对原子阻尼系数α的影响。从图中可以看出, 在激光强度较小及频率失谐较小的条件下，阻尼系数与这两个参量基本呈线性关系，而当激光频率失谐大于-0.5Γ时, 系数α出现饱和并且开始随激光频率失谐量的增大而降低。因此只有在适当的激光光强和频率失谐值条件下，才能获得最佳的阻尼及耗散力，使原子得到最佳冷却效果。分析在1维冷却光场中的锶原子，冷却跃迁所采用的能级为(5s2)1S0~(5s5p)1P1，对应辐射波长461nm，则单光子动量为14.37×10-28kg·m/s，从而得到此时锶原子所受到的最大耗散力为14.37×10-20N。具体计算得到耗散力对应的加速度为9.98×105m/s2。
Figure 2. Friction coefficient varying with laser intensity and frequency detunning
当1维驻波激光场强度一定时(取s=0.1)，不同光场频率失谐条件下原子所受激光场耗散力在相应速度区间的变化如图 3所示。其中图 3a~图 3d分别为δ1=-0.1Γ，δ2 =-0.5Γ，δ3 =-1.5Γ，δ4 =-3Γ 4种激光频率失谐条件下的耗散力。由图可得出，当激光为一定频率负失谐量且在小失谐情况下，散射力与速度成线性关系且方向相反，并且可以看出随激光光场频率失谐的增加，耗散力显示出逐渐增大的特点。但光场频率失谐量并非越大越好，当超过一定失谐量时耗散力达到饱和，并且此时耗散力与原子速度之间不存在线性关系。
Figure 3. Relationship between dissipative force and velocity under different laser frequency detuning
接下来分析在激光场频率失谐一定条件下原子所受耗散力状况。图 4中给出了1维驻波光场的失谐量一定时(δ=-0.5Γ)，不同光场强度条件下原子所受激光场耗散力在相应速度区间的变化趋势。从图中可以看出, 当原子处于光强较弱的光场中时，即饱和参量的数值较小时，原子所受耗散力随饱和参量的增大而逐渐增加，但是当激光光场强度(与饱和参量呈正比关系)增加到一定程度时耗散力呈现饱和，这意味着高光场强度下，原子的上下能级平均布居，耗散力达到最大值Fmax=ħkΓ/2。
Figure 4. Relationship between dissipative force and velocity under different laser intensities
-
冷原子可以通过多束激光交叠的光学粘团方法实现，但是磁光阱(magneto-optical trap，MOT)装置是最有效和简便的途径，通过磁光阱原子可被稳定地冷却陷俘于真空气室中。最初磁光阱被用于碱金属原子的冷却与俘获，而后被用于碱土金属原子中。在磁光阱中原子在3维方向均受到耗散力的作用，以原子在z方向受到的耗散力为例：
$ \mathit{\boldsymbol{F}} = h\mathit{\boldsymbol{k}}\frac{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}}{2}\left\{ {\frac{s}{{1 + s + {{[2(\delta - {\bf{k}} \cdot {\bf{v}} - \mu {\rm{d}}B \cdot z)/\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}]}^2}}} - \frac{s}{{1 + s + {{[2(\delta + \mathit{\boldsymbol{k}} \cdot \mathit{\boldsymbol{v}} + \mu {\rm{d}}B \cdot z)/\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}]}^2}}}} \right\} $
(5) 式中，μ是上下两能级跃迁的有效磁矩，dB代表磁场强度变化率。在z方向原子在此力作用下做阻尼运动。基于锶原子(5s2)1S0~(5s5p)1P1跃迁的MOT中原子受到的最大耗散力与重力之比通过耗散力与重力之比可知，在此能级跃迁下重力对原子的作用可忽略不计。
磁光阱中每一个自由度上的原子温度与其速度大小都有关联, kBT/2=mv2/2，其中kB为玻尔兹曼常数。在热平衡条件下又有αv2=D/m，其中α=-8ħ - k2δ(s/Γ)/[1+s+(2δ/Γ)2]2为MOT阻尼系数，为扩散系数，它与每一个吸收光子数目的涨落、原子在光子无规作用下动量随机涨落均有关系。通过分析得到MOT中锶原子的温度计算表达式：
$ T = \frac{D}{{{k_{\rm{B}}}\alpha }} = - \frac{{ħ{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^2}\left[ {1 + s + {{\left( {\frac{{2\delta }}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}}} \right)}^2}} \right]}}{{8{k_{\rm{B}}}\delta }} $
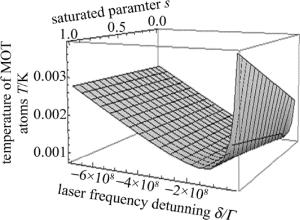
(6) 基于锶原子(5s2)1S0~(5s5p)1P1能级跃迁的磁光阱MOT冷却原子温度结果如图 5所示。从图中可以看出, 锶原子温度受MOT区激光强度的影响，随激光光强的增强而变高，且只有激光频率失谐在-0.5Γ(ΓSr=2×108)对应的锶原子冷却温度有最小值。再通过分析激光光场失谐与温度的变化趋势图，发现当激光频率失谐量远离-0.5Γ时，对应的MOT原子温度值是越来越高。综合分析可以得出当激光频率失谐为自然跃迁线宽的一半时，即δ=2π-1 Γ/2=-16MHz，得到锶原子在磁光阱中的最低冷却温度Tmin≈0.76mK。
Figure 5. Relationship between temperature of MOT atoms and laser intensity with different frequency detunning
-
基于激光冷却的理论分析，得到碱土金属中性锶原子在1维驻波场中受到最大耗散力14.37×10-20N，对应最大加速度9.98×105m/s2。与耗散力相关的阻尼系数在弱光场、小频率失谐条件下会随光强和频率失谐的增加而增大。在1维驻波光场中锶原子所受耗散力受激光强度和频率失谐量的影响明显，当光强一定时，频率失谐量由小增大时，原子受力在速度区间内逐渐增大并达到饱和，且与原子速度由线性变为非线性关系，当频率失谐量一定时，光强由弱变强时原子受力逐渐增大并饱和至Fmax=ħkΓ/2。此外得到中性锶原子在3维(5s2)1S0~ (5s5p)1P1磁光阱中的冷却温度受激光光场强度及频率失谐量的影响趋势，以及最终得到锶原子被冷却的最低温度Tmin≈0.76mK。该理论计算温度与世界各研究小组的实验结果一致，冷原子温度在几个毫开甚至更低。但相较于该理论温度，研究小组实验获得的冷原子温度略高于该理论值，这是由于加热机制的存在导致理论和实验值之间的差异[19]。基于激光冷却技术的锶原子特性研究，本文中详细描述了多普勒冷却光场中的锶原子特性，为同类碱土金属原子的冷却提供了理论基础。综上而言，冷原子尤其碱土金属冷原子以其丰富的的特性备受科学家们青睐，并成为了广大科学研究领域的理想媒介，相信会对科技发展产生深远影响。
基于激光冷却技术的中性锶原子特性研究
Study on characteristics of neutral strontium atoms based on laser cooling technique
-
摘要: 为了研究碱土金属类的中性锶原子在多普勒冷却激光场中的冷却特性，从Heisenberg方程出发，采用激光冷却理论分析得到锶原子在能级跃迁（5s2）1S0~（5s5p）1P1 1维驻波激光光场和3维磁光阱中冷却效果与激光强度、失谐量等冷却激光场参量的关系。结果表明，当锶原子处在1维驻波激光光场中且在弱激光光场、频率小失谐条件下，锶原子所受耗散力与这两个参量呈线性关系，但当两个参量增长至一定程度时耗散力呈现饱和现象；当锶原子在3维磁光阱中且当阱中激光光场的频率失谐为-16MHz时，碱土金属锶原子有最低冷却温度，约为0.76mK。对多普勒冷却光场中性锶原子特性的分析为其它碱土金属类原子的冷却研究提供了一定的理论指导。Abstract: In order to study cooling characteristics of neutral Sr of alkaline-earth metal in a Doppler cooling laser field, the relationship between the cooling results of strontium atomic in 1-D laser standing wave light field with energy level transition (5s2)1S0~(5s5p)1P1 and 3-D magneto-optical trap and laser parameters, including laser intensity and frequency detuning, was obtained by using the theory of laser cooling based on Heisenberg equations. The results show that, when the strontium atoms are in 1-D standing wave laser field and under the condition of weak laser field and frequency detuning, the dissipation force of strontium atoms is linearly related to the two parameters. But when the two parameters increase to a certain degree, the dissipative force is saturated. When strontium atoms are in 3-D magneto-optical trap and frequency detuning of laser light field in the traps is -16MHz, alkaline-earth metal strontium atoms have the lowest cooling temperature of 0.76mK. The characteristics analysis of neutral strontium atoms in Doppler cooling field provides some theoretical guidance for cooling study on other alkaline-earth metal atoms.
-
Figure 1. Relationship between dissipative force of 1-D laser standing wave and atomic velocity
Figure 3. Relationship between dissipative force and velocity under different laser frequency detuning
Figure 4. Relationship between dissipative force and velocity under different laser intensities
-
[1] HANSCH T W, SCHAWLOW A L. Cooling of gases by laser radiation[J]. Optics Communications, 1975, 13(1):68-69. doi: 10.1016/0030-4018(75)90159-5 [2] CHRISTENSEN B T R, HENRIKSEN M R, SCHAFFER S A, et al. Non-linear spectroscopy of Sr atoms in an optical cavity for laser stabilization[J]. Physical Review, 2015, A92(5):053820. [3] DAREAU A, SCHOLL M, BEAUFILS Q, et al. Doppler spectroscopy of an ytterbium bose-einstein condensate on the clock transition[J]. Physical Review, 2015, A91(2):023626. [4] GERTIS J, FRIESDORF M, RIOFRIO C A, et al. Estimating strong correlations in optical lattices[J]. Physical Review, 2016, A94(5):053628. [5] WEINER J, BAGNATO V, ZILIO S, et al. Experiments and theory in cold and ultracold collisions[J]. Reviews of Modern Physics, 1999, 71(1):1-85. [6] USHIJIMA I, TAKAMOTO M, DAS M, et al. Cryogenic optical lattice clocks[J]. Nature Photonics, 2015, 9:185-189. doi: 10.1038/nphoton.2015.5 [7] LI Y Q, XIONG X M, ZHANG W T. 3-D analysis of laser-cooling Cr atoms[J]. Laser Technology, 2012, 36(6):788-792(in Chinese). [8] WILLIAM D P. Laser cooling and trapping of neutral atoms[J]. Reviews of Modern Physics, 1998, 70(3):721-741. doi: 10.1103/RevModPhys.70.721 [9] WANG Y Q. Laser cooling and trapping of atoms[M]. Beijing:Peking University Press, 2007:336-383(in Chinese). [10] BALYKIN V I, LETOKHOV V S, MUSHIN V I. Observation of the cooling of free sodium atoms in a resonance laser field with a scanning frequency[J]. JETP Letters, 1979, 29(10):560-564. [11] CHU S, HOLLBERG L, BJORKHOLM J E, et al. Three-dimensional viscous confinement and cooling of atoms by resonance radiation pressure[J]. Physical Review Letters, 1985, 55(1):48-51. doi: 10.1103/PhysRevLett.55.48 [12] IAN N. Laser cooling and trapping of neutral calcium atoms[D]. Glasgow, UK: University of Strathclyde, 2009: 9-23. [13] ZHOU M, XU X Y. Advances in the precision spectroscopy of cold ytterbium atoms[J]. Physcis, 2016, 45(7):431-440(in Ch-inese). [14] LIU H, GAO F, WANG Y B, et al. Precision frequency measurement of 1S0-3P1 intercombination lines of Sr isotopes[J]. Chinese Physics, 2015, B24(1):013201. [15] SORRENTION F, FERRARI G, POLI N, et al. Laser cooling and trapping of atomic strontium for ultracold atoms physics, high-precision spectroscopy and quantum sensors[J]. Modern Physics Letters, 2006, B20(21):1287-1320. [16] MICKELSON P G, MARTINEZ de ESCOBAR Y N, ANZEL P, et al. Repumping and spectroscopy of laser-cooled Sr atoms using the (5s5p)3P2-(5s4d)3D2 transition[J]. Journal of Physics, 2009, B42(23):235001. [17] WANG S K, WANG Q, LIN Y G, et al. Cooling and Trapping 88Sr atoms with 461nm laser[J]. Chinese Physics Letters, 2009, 26(9):093202. doi: 10.1088/0256-307X/26/9/093202 [18] TANNOUDJI C C, ODELIN D G. Advances in atomic physics[M]. Singapore City, Singapore:World Scientific Publishing Co.Pte.Ltd., 2011:243-267. [19] THIERRY C, JEAN-LOUIS M, ROBIN K, et al. Extra-heating mechanism in Doppler cooling experiments[J]. Journal of the Optical Society of America, 2005, B22(9):1819-1828. -
点击查看大图
图(5)
计量
- 文章访问数: 9051
- HTML全文浏览量: 6888
- PDF下载量: 230
- 被引次数: 0
