网站地图
-
激光波前曲率半径是激光束传输空间某位置处等相位面的曲率半径，简称波前曲率半径，是激光束腰位置的主要影响因素[1-2]。对于激光雷达、激光武器、激光通信等激光发射系统，波前曲率半径的精确测量是预测激光束空间功率密度分布的重要参量[3]。波前曲率半径的测量常采用哈特曼波前传感器、剪切干涉仪、波前曲率传感器等仪器。哈特曼波前传感器经过长期发展，已经比较成熟，但子孔径阵列很大时，微透镜阵列的设计加工及波前重构数据处理的难度均很大[4-5]。剪切干涉仪通过干涉条纹数量及形态解算波前曲率半径，其对波前曲率半径的测量精度较低、测量范围有限。曲率波前传感器是目前研究比较广泛的一种测量方法[6]。1998年，Qinetiq公司提出采用多路成像衍射光栅的波前曲率测量方法，该光栅给不同衍射级引入了不同程度的散焦，通过不同衍射级的光斑尺寸及光强分布实现波前曲率半径的测量[7]。2004年, 英国的Arden光子公司应用该光栅生产了目前唯一商用的光栅型波前曲率传感器AWS-50[8]。国内，国防科技大学对光栅型波前曲率传感器进行了大量研究，并应用在固体激光器热透镜效应引起的波前曲率半径变化的精确测量[9-11]。
泰伯-莫尔条纹技术是基于光栅的自成像效应和莫尔条纹效应进行测量的一种技术。平行光束连续通过两个光栅，利用一个光栅的自成像与第2个光栅栅线的叠加形成莫尔条纹，通过莫尔条纹的变化即可得到被测量，该方法已广泛应用于位移、小角度、长焦距等参量的高精度测量[12-13]。对于激光波前曲率半径的测量，与长焦距测量方法相似，通过莫尔条纹倾角的变化求解激光波前曲率半径，具有测量范围大、精度高、不受激光束束宽和波长限制等优点，特别适合大口径激光发射系统出射激光波前曲率半径的高精度测量。
-
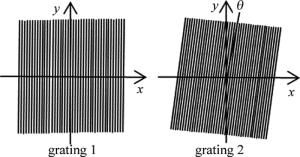
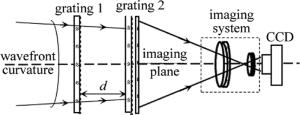
系统采用泰伯-莫尔条纹技术测量激光束波前曲率半径，被测激光束直接由光栅1进入测量系统。测量系统结构如图 1所示。测量系统主要光栅1、光栅2、成像屏、成像系统、数字CCD组成，其中光栅1和光栅2的间距为d，两光栅栅线之间存在一个很小的角度θ。
Figure 1. System structure
以光栅1平面为x-y面，光栅中心为坐标原点，光束传播方向为z轴建立坐标系。若设被测激光束波前曲率半径为R，被测波前看作标准球面波，其复振幅可表示为：
$ U = \frac{{{a_0}}}{R}{\rm{exp}}\left( { - {\rm{i}}\frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }\frac{{{x^2} + {y^2}}}{{2R}}} \right) $
(1) 式中, a0为与光强有关的常数，λ为被测激光波长。光栅1的刻线方向与坐标轴y轴平行，光栅2的刻线方向与坐标轴y轴正向存在夹角θ，也即光栅1和光栅2的栅线夹角为θ，则光栅复振幅透过率分别表示为：
$ \left\{ \begin{array}{l} {g_1}\left( {x, y} \right) = \sum\limits_{ - \infty }^\infty {} {b_m}{\rm{exp}}\left( {{\rm{i}}\frac{{2{\rm{ \mathsf{ π} }}}}{p}mx} \right)\\ {g_2}\left( {x, y} \right) = \sum\limits_{ - \infty }^\infty {} {c_n}{\rm{exp}}\left[ {{\rm{i}}\frac{{2{\rm{ \mathsf{ π} }}}}{p}n(x{\rm{cos}}\theta - y{\rm{sin}}\theta )} \right] \end{array} \right. $
(2) 式中, bm, cn分别为光栅1和光栅2不同衍射级次的衍射效率，p为光栅周期。则被测波前经过光栅1后，光波复振幅分布为：
$ \begin{array}{l} U(x, y, {0^ + }) = \sum\limits_{ - \infty }^\infty {} {b_m}\frac{{{a_0}}}{R}{\rm{exp}}\left( { - {\rm{i}}\frac{{{m^2}\pi \lambda R}}{{{p^2}}}} \right) \times \\ {\rm{exp}}\left[ {{\rm{i}}\frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }\frac{{{{\left( {x + m\lambda R/p} \right)}^2} + {y^2}}}{{2R}}} \right] \end{array} $
(3) 若光栅1与光栅2间距满足下式:
$ d = \frac{{m{p^2}}}{{\lambda - \frac{{m{p^2}}}{R}}}, \left( {m = 0, \pm 1, \ldots } \right) $
(4) 则光栅2前光强分布为：
$ \begin{array}{l} I\left( {x, y, d} \right) = {c_0} + \\ {c_1}{\rm{cos}}\left\{ {\frac{{2{\rm{ \mathsf{ π} }}}}{p}\left[ {\frac{{Rx}}{{2\left( {R + d} \right)}} + \frac{{dR{\rm{sin}}\theta }}{{R + d}}} \right]} \right\} + O(x) \end{array} $
(5) 式中，O(x)是关于x的高频信息。由(5)式可得泰伯自成像的光强为周期性条纹分布，其周期可表示为：
$ p\prime = \frac{{\left( {R + d} \right)p}}{R} $
(6) 泰伯自成像周期是光栅周期、光栅间距和波前曲率半径的函数，且当趋向无穷大时，光强分布和光栅的形态是完全相同的，像的周期仍为p。
系统采用两块周期相同的光栅作为周期物体，其中光栅1的泰伯像可以认为是光栅在球面照射下的简单变形，其与光栅2相互叠加将在光栅2后表面上将形成莫尔条纹。
两个光栅的形态如图 2所示。光栅栅线的夹角为θ，莫尔条纹与x轴的夹角为φ，则其和光栅1的泰伯像周期p′及光栅2周期p之间的关系如下式所示[11]:
$ {\rm{sin}}\varphi = \frac{{p\prime {\rm{sin}}\theta }}{{{{(p{\prime ^2} + {p^2} - 2p\prime p{\rm{cos}}\theta )}^{1/2}}}} $
(7) 
Figure 2. Grating pattern
将(6)式代入(7)式中，得到波前曲率半径测量表达式：
$ R = d + \frac{d}{{{\rm{cos}}\theta + {\rm{sin}}\theta {\rm{tan}}\varphi - 1}} $
(8) 当测量系统中光栅间距d、光栅栅线夹角θ确定，则被测光束波前曲率半径R与莫尔条纹倾角φ存在如(8)式所示关系，可实现对激光束波前曲率半径的测量。
-
测量系统的主要参量为光栅间距、光栅栅线夹角，两个参量直接决定了测量系统性能。以测量理论为基础建立理论仿真分析模型，模拟得到不同光栅栅线夹角下莫尔条纹图像，如图 3所示。
Figure 3. Moiré fringe of different grating angles
对比4幅图，莫尔条纹周期随光栅夹角的增大而变小，当夹角为0.001°时，莫尔条纹仅有一根条纹；当光栅夹角为0.5°时，条纹数量为26条；当夹角为1°时，莫尔条纹周期明显变小；当夹角为3°时，图像中已经很难看出莫尔条纹的形态，这是由于其超出模拟的最大分辨率，因此必须控制光栅栅线夹角大于0.5°而小于3°。
由(4)式可知，光栅间距直接影响莫尔条纹的对比度，如图 4所示。图 4a中m=500；图 4b中m=500.25；图 4c中m=500.5。
Figure 4. Moiré fringe of different grating spacings
不同光栅间距下莫尔条纹的对比度明显不同，当m=500时，莫尔条纹对比度最好，条纹清晰。在选择系统参数时，m为整数值时，条纹对比度最好，但由光栅间距分析可知，随着被测曲率半径的光栅间距不同，因此在整个测量范围光栅间距就不可能完全处在理论最优位置，在测量过程中必须根据条纹对比度实时调整光栅间距。
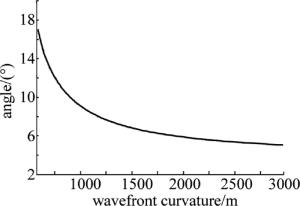
根据以上分析建立光栅栅线夹角为1°，光栅间距为300mm的模型，此时莫尔条纹倾角随被测波前曲率半径的变化曲线如图 5所示。在500m~3000m范围内莫尔条纹倾角变化约为10°。
Figure 5. Relationship between angle of Moiré fringe and curvature radius
-
系统波前曲率半径计算公式如(8)式所示，对测量公式两边同时微分得各不确定度影响因素影响因子为：
$ \left\{ \begin{array}{l} {k_1} = \frac{{{\rm{d}}R}}{{{\rm{d}}d}} = 1 + \frac{1}{{{\rm{cos}}\theta + {\rm{sin}}\theta {\rm{tan}}\varphi - 1}}\\ {k_2} = \frac{{{\rm{d}}R}}{{{\rm{d}}\theta }} = \frac{{d({\rm{sin}}\theta - {\rm{cos}}\theta {\rm{tan}}\varphi )}}{{{{({\rm{cos}}\theta + {\rm{sin}}\theta {\rm{tan}}\varphi - 1)}^2}}}\\ {k_3} = \frac{{{\rm{d}}R}}{{{\rm{d}}\varphi }} = \frac{{{\rm{sin}}\theta {{({\rm{sec}}\varphi )}^2}}}{{{{({\rm{cos}}\theta + {\rm{sin}}\theta {\rm{tan}}\varphi - 1)}^2}}} \end{array} \right. $
(9) 因此影响系统的测量不确定度的主要因素有：(1)光栅间距引入的测量不确定度u1。光栅间距采用游标卡尺测量，按B类评定，其测量分辨力为0.05mm，假定其服从矩形分布，则光栅间距的测量不确定度为0.03mm，影响因子为k1; (2)光栅栅线夹角引入的测量不确定度u2。光栅栅线夹角采用采用CCD采集光栅栅线进行测量，并利用自准直仪进行验证，按A类进行评定，因此光栅栅线夹角的测量不确定度为18″，影响因子为k2; (3)莫尔条纹倾角引入的测量不确定度u3。莫尔条纹倾角采用傅里叶变换结合迭代算法进行求解，按B类评定，根据文献资料，莫尔条纹倾角的解算不确定度为30″[14-15]，影响因子为k3。
$ {u_{\rm{c}}} = \frac{{\sqrt {{u_1}^2 + {u_2}^2 + {u_3}^2} }}{{R}} $
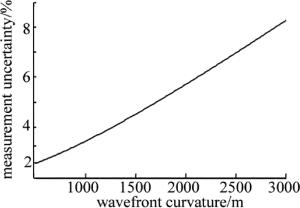
(10) 按(10)式计算测量系统波前曲率半径相对合成测量不确定度uc，则测量系统相对测量不确定度随被测波前曲率半径的变化曲线图，如图 6所示。
Figure 6. Relationship between measurement uncertainty and curvature radius
系统的相对不确定度随被测曲率半径的增大而增加，在被测曲率半径为500m时，系统的相对不确定度为2.0%(包含因子k=2)，当被测曲率半径为3000m时, 系统的相对不确定度为7.3%(包含因子k=2)。
-
按图 1建立实验系统，系统通光口径200mm，通过现场校准系统参量的方式对实验系统进行校准，并采用刀口仪找束腰半径的方式验证校准不确定度。对物镜焦距为3.44m的激光发射系统进行测量，当采用束腰半径计算波前曲率半径为500m时，采集莫尔条纹，采用傅里叶变换结合迭代法对莫尔条纹倾角进行解算，代入(8)式计算测量结果。重复测量12次，测量结果如表 1所示。测量结果平均值为498.4m，测量重复性为0.17%，测量结果相对于刀口仪找束腰位置的方法的偏差为0.4%。
Table 1. Measurement result
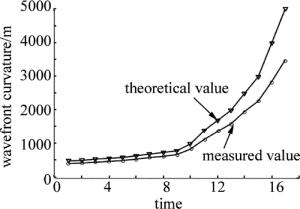
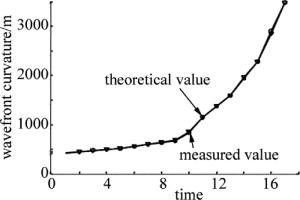
times 1 2 3 4 5 6 7 8 9 10 11 12 results/mm 494 500 503 497 501 499 499 498 495 499 496 500 移动发射天线目镜位置，改变出射激光波前曲率半径，重复测量12次求其平均值。测量结果与理论值的对比曲线如图 7所示。
Figure 7. Comparison of the measured and theoretical values
由图 7可知, 理论值和测量值存在明显偏差，并且随波前曲率半径的增大而增大，最大偏差达到30%，这是因为大口径激光发射系统物镜焦距均较大，焦距的测量不确定度相对较大，而且易受温度、振动等环境因素影响，因此在应用前需对其进行校准。
激光发射系统出射波前曲率半径理论值的计算是按发射天线后截距计算，步骤如下：首先采用ZYGO干涉仪调节发射天线，当其离焦量最小时认为出射波前曲率半径为无穷大，记录发射天线目镜位置；然后测量物镜焦距，记为f；最后根据如下式的牛顿公式计算出射波前曲率半径理论值R:
$ R = \frac{{{f^2}}}{{\Delta l}} $
(11) 式中, Δl为目镜相对移动距离。
在物镜焦距测量完成后波前曲率半径的控制通过控制目镜的相对移动距离实现，但仅改变目镜的移动距离无法实现波前曲率半径全范围内的校准。本文中采用最小二乘拟合法同时对物镜焦距、目镜相对移动距离进行校准。图 8为校准完成后理论值与测量值的关系曲线。主镜焦距校准结果为3.25m，目镜移动距离偏差为0.71mm，校准完成后理论值与测量值的最大偏差为2%。
Figure 8. Comparison of the measured and theoretical values after calibration
-
理论验证了以泰伯-莫尔条纹技术为基础的波前曲率半径测量方法的可行性，该测量方法可实现大口径、大曲率半径激光束波前曲率半径的精确测量。当被测波前曲率半径为500m时, 系统相对不确定度为2.0%(k=2);当被测波前曲率半径为3000m时, 系统相对不确定度为7.3%(k=2)。测量了口径200mm、物镜焦距3.44m的激光发射系统出射激光波前曲率半径，当测量结果为498m时，测量重复性为0.2%，与实际位置相对偏差为0.4%。根据测量结果实现了激光器出射波前曲率半径、物镜焦距、目镜位置等参量的校准，校准完成后波前曲率半径理论值与测量值最大偏差为2%。
基于泰伯-莫尔条纹的激光波前曲率半径测量
Measurement of laser wavefront curvature radius based on Talbot-Moiré fringe
-
摘要: 为了精确测量激光波前曲率半径，提出了基于泰伯-莫尔条纹技术的波前曲率半径测量方法，建立了激光波前曲率半径测量理论分析模型。对波前曲率半径与莫尔条纹倾角的关系、系统测量不确定度进行了分析，完成了激光波前曲率半径测量系统的设计，构建了测量系统，并对口径为200mm的激光发射系统的出射波前曲率半径进行了测量。结果表明，测量结果为498m时，测量重复性为0.2%，根据测量结果推算光束束腰位置与实际位置相对偏差为0.4%；并根据500m~3000m的测量结果对激光发射系统中出射波前曲率半径、物镜焦距、目镜位置等参量进行了校准，校准完成后与理论值的最大偏差为2%。该方法能够实现大口径激光发射系统出射波前曲率半径的高精度测量。Abstract: In order to measure curvature radius of laser wavefront accurately, one method based on Talbot-Moire fringe technique was proposed. The theoretical model of measuring wavefront curvature radius was established. The relationship between wavefront curvature radius and angle of Moire fringe, and the measurement uncertainty of the system were analyzed. The measurement system was designed and constructed. Wavefront curvature radius of laser system with the diameter of 200mm was measured. The results show that, the repeatability of measurement is 0.2% when the measured result is 498m. The relative deviation between the waist position and the actual position of the beam is 0.4%. According to the measured results of 500m~3000m, the parameters such as wavefront curvature radius, the focal length of object and the position of eyepiece are calibrated. After calibration, the maximum deviation from the theoretical value is 2%. The method can achieve high precision measurement of wavefront curvature radius of laser launching system with large aperture.
-
Key words:
- laser technique /
- measurement of curvature radius /
- Moiré fringe /
- laser emission system
-
Table 1. Measurement result
times 1 2 3 4 5 6 7 8 9 10 11 12 results/mm 494 500 503 497 501 499 499 498 495 499 496 500 
下载: 导出CSV
-
[1] MA Z R, WANG Sh D.Carrier-envelope phase shift of chirped pulsed Gaussian beam with varied pulse duration[J]. Laser Technology, 2010, 34(5):701-703(in Chinese). [2] ZHOU R Zh, YAN J X, YU X.Adaptive optics[M]. Beijing:National Defence Industry Press, 1996:54-65(in Chinese). [3] GUO Sh Y, HU X, YAN Zh A, et al. Research development of space-borne lidar in foreign countries[J]. Laser Technology, 2016, 40(5):772-778(in Chinese). [4] BLANCHARD P M, GREENAWAY A H.Simultaneous multiplaneimageing with a distorted with diffraction grating[J]. Applied Optics, 1999, 38(32):6692-6699. doi: 10.1364/AO.38.006692 [5] WOODS S C, GREENAWAY A H.Wavefront sensing by use of a Green's function solution to the intensity transport equation[J]. Journal of the Optical Society of America, 2003, A20(3):508-509. [6] BLANCHARD P.Phase-diversity wavefront sensing with a distorted diffraction grating[J]. Applied Optics, 2000, 39(35):6649-6655. doi: 10.1364/AO.39.006649 [7] RODDIERF. Curvature sensing and compensation:a new concept in adaptive optics[J]. Applied Optics, 1988, 27(7):1223-1225. doi: 10.1364/AO.27.001223 [8] SHEN H B.Study on restoration algorithm of grating wavefront curvature sensor[D]. Changsha: National University of Defense Technology, 2005: 54-56(in Chinese). [9] DIAO F J, JIANG Z F, XU X J.Influence of non-uniform distribution of light intensity on wavefront curvature sensor[J]. Acta Optica Sinica, 2006, 26(9):1293-1296(in Chinese). [10] YANG K T, LIAO Zh Sh, TAO J G.Analysis of Talbot image symmetry about Fourier spectrum plane and measurement of focal length[J]. Acta Optica Sinica, 1994, 14(1):50-54(in Chinese). [11] YANG S, YUN Y, CHEN A Zh.Spatial phase-shifting characteristic of double grating interferometer[J]. Optics Express, 2011, 17(22):20415-20429. [12] DHANOTIA J, PRAKASH S.Collimation testing using coherent gradient sensing[J]. Optics and Lasers in Engineering, 2011, 49(12):1185-1189. [13] LU H, CHEN H, HE Y, et al. Alignment method for measurement of long focal length based on Talbot-Moiré effect[J]. Infrared and Laser Engineering, 2013, 42(10):2836-2841(in Chinese). [14] CHEN H, HE Y, LI J X, et al. Measurement of long focal lengths with a double-grating interferometer[J]. Applied Optics, 2013, 52(27):6696-6702. doi: 10.1364/AO.52.006696 [15] HOU Ch L, BAI J, HOU X Y. The measurement of long focal length based on Talbot effect of Ronchi grating[J]. Acta Optica Sinica, 2002, 22(11):1328-1330(in Chinese). -
点击查看大图
图(8) / 表(1)
计量
- 文章访问数: 5693
- HTML全文浏览量: 3474
- PDF下载量: 262
- 被引次数: 0
