-
超强激光与固体靶相互作用是产生极紫外(extreme ultraviolet,EUV)-软X射线波段相干辐射以及基于高次谐波(high-order harmonic generation,HHG)实现阿秒脉冲的重要途径[1]。相比较于激光与气体介质相互作用高次谐波的产生[2-3],激光与固体靶方案可以承受超高强度的激光,大量电子可以在强激光场中进行充分的非线性运动,电子轨迹由多个激光吸收机制决定[4-5],从而可以实现辐射强度较高的高次谐波。对于激光与固体靶相互作用中高次谐波的产生,人们在理论和实验方面进行了广泛的研究[6]。
超强激光与固体平面靶(厚度远大于趋肤深度)相互作用,已经被证实了在反射方向由相对论振荡镜面机制(relativistically oscillating mirror,ROM)[7]主导的高次谐波产生,并可以诱导产生高光束质量[8]和阿秒脉宽[9]的EUV辐射明亮光源。BULANOV[10-11]等人提出,ROM机制即激光入射到等离子体表面后,电子在激光有质动力作用下向等离子体内部运动,随着电子密度不断增加,电子被压缩而离子不动,等离子体中由电子与离子分离产生的静电分离场与激光有质动力共同作用下,激光不再继续向前运动,而反向朝等离子体外运动,此时的反射面即“镜面”,其电子密度即临界密度。在反射方向上,反向的电子与入射的激光脉冲产生的多普勒效应导致了高次谐波的产生,高次谐波特点为相位锁定的,所以,对反射方向信号进行适当滤波即能得到阿秒脉冲甚至亚阿秒脉冲。
受到离子加速[12-13]方案的启发,近年来超短超强(激光强度I>1020W/cm2)激光脉冲与薄膜靶(厚度小于趋肤深度)相互作用产生高次谐波的方案也得到了关注。在薄膜靶情况下,电子与离子分离产生的分离场与激光有质动力不再比较,等离子体中的电子受有质动力的驱动下在短时间内全部离开固体靶区域,此时振荡镜面机制不再适用。2010年,有学者提出了相干同步辐射(coherent synchrotron emission,CSE)机制[14-15],即在等离子体与真空界面处,电子离开固体靶后可以周期性地形成致密的纳米电子团簇,并在相对论激光有质动力作用下,沿着传播方向不断加速,从而在透射方向产生强烈的同步辐射谐波信号。然而对于厚度较薄的固体靶,其反射方向的谐波性质并不清楚。
本文中通过基于粒子云网格算法(particle-in-cell,PIC)的模拟方法,研究了正入射超强激光脉冲与高密度等离子体薄膜靶相互作用产生高次谐波辐射的特征,尤其是反射方向的谐波辐射场。
-
本文中采用PIC粒子模拟方法研究激光与薄膜靶相互作用。PIC算法是将空间划分成若干网格,等离子体中的电子和离子用若干“宏粒子”表示,每个宏粒子代表许多个实际的带电粒子[16]。开始,将粒子累积到空间网格上,激光入射到等离子体区域,粒子在电磁场作用下开始运动,根据洛伦兹方程可以求解粒子的运动,同时,粒子的运动也会产生电磁场,并通过麦克斯韦方程求解该电磁场。PIC模拟过程中,空间和时间都是离散化的,每一个时间步都要计算出所有宏粒子的速度和位置以及电磁场的空间分布,然后用当前时刻的所有粒子和电磁场信息去计算下一个时间步各物理量的信息。由于PIC粒子模拟的思路比较固定,当前已经形成了一些专用于PIC模拟的程序。而作者工作中所用的VSIM 6.2[17]就是其中一个典型的粒子模拟程序,可以模拟1维~3维情形下的激光-等离子体相互作用过程。对于高强度激光与固体靶相互作用,实际实验中,脉冲前沿很小一部分就足以使相互作用区域的固体靶物质迅速地完全电离形成致密等离子体,而脉冲的主要部分是与所产生的致密等离子体相互作用的。因此对于这个过程的PIC模拟,通常直接设置固体靶为致密等离子体,而忽略激光与固体靶相互作用中的电离过程。
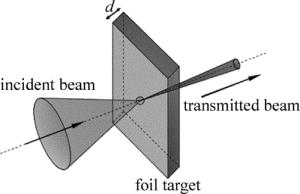
本文中利用VSIM 6.2软件,采取1维PIC模拟。模拟示意图如图 1所示。在靶区域左侧位置设定为坐标原点。激光脉冲从左侧正入射到等离子体区域,同时设置脉冲只向右传, 入射激光为线偏振光,波长λ=800nm,激光脉冲时间包络为超高斯包络,脉冲持续时间为50fs(19T0),其中T0=λ/c, c为光速, 设置23个光周期。模拟中设置归一化入射脉冲强度a0=20,其中$ {a_0} = \frac{{eE}}{{{m_{\rm{e}}}{\omega _{\rm{l}}}c}} = \sqrt {I{\lambda ^2}/(1.37 \times {{10}^{18}}{\rm{W}}\cdot{\rm{ \mathsf{ μ} }}{{\rm{m}}^2}\cdot{\rm{c}}{{\rm{m}}^{ - 2}})} $ (me为电子质量,ωl为激光频率,e为电子密度,E为入射激光电场强度),相当于激光峰值强度I=8.56×1020W/cm2,等离子体电子密度设为Ne=800Nc(临界等离子体密度Nc=ε0ωl2me/e2, ε0为真空介电常数)。1维x方向模拟尺寸23λ,模拟网格分辨率为2000cells/λ,每个网格宏粒子数为3500。等离子体靶初始位置设置为x=0处,初始设置靶厚度d=200nm,并以25nm区间改变靶厚度,靶前设置密度标长为100nm线性等离子体密度梯度。
-
靶厚度在200nm以下时如图 2所示。在透射方向上,阶次n < 28的谐波强度受到强烈抑制。而对于n>28阶谐波,谐波强度明显增大。谐波阶次在n < 47阶可以看到明显的谐波峰值分布,且随着阶次的增加, 谐波谱的衰减较小,并且可以观察到,改变靶的厚度,谐波阶次并无明显变化。
模拟中设置固体靶等离子体密度为Ne=800Nc,有$ {\omega _{{\rm{p, max}}}}/{\omega _l} = \sqrt {{N_{{\rm{e, max}}}}/{N_{\rm{c}}}} = {800^{1/2}} \approx 28$,其中ωp, max为最大等离子体频率,Ne, max为靶的最大电子密度。低于ωp, max(28ωl)的电磁波在等离子体中强烈的衰减而高于ωp, max的电磁波则可以通过等离子体,在模拟结果中(见图 2、图 3)都观察到透射方向上阶次n < 28的谐波强度受抑制,说明在相互作用过程中,整个固体靶区域仍然保持固体等离子体密度,并没有被强激光脉冲的作用“穿透”。继续增加靶厚度,观察在靶厚度在200nm以上时透射方向谐波分布。在靶厚度超过200nm时,如图 3所示。观察到谐波阶次有明显提升, 而且可以看到十分明显的谐波峰,且主要体现为奇数阶次的谐波。

Figure 3. Harmonic distribution along the transmission direction a—target thickness of 200nm b—target thickness of 250nm
CSE谐波是由于靶面的高密度电子团簇的形成[14-15]并在激光场和离子-电子静电分离场的共同作用下加速,所产生的后向CSE谐波辐射经过固体靶等离子体的“自滤波”作用,从而形成了这样的低阶次谐波受抑制的谐波分布特征。对于不同的厚度,后向的谐波谱特征有明显的差别,尤其是厚度小于200nm和大于200nm的两种情形。后者的谐波强度高于前者,而且可以观察到明显独立谐波阶次。说明后向的CSE谐波对固体靶厚度有较强的依赖性,并且为了得到更好的后向CSE谐波辐射,固体靶厚度不能太小。过小的固体靶厚度可能不利于高密度电子团的形成和加速,因此使得后向CSE谐波弱化。在透射方向上,谐波谱中只包含奇数阶次的谐波分布,这说明,在一个光周期内,电子团簇分别受上下两个半光周期的脉冲作用而出现两次明显的加速,产生两次高频辐射,在频谱中便体现为明显的奇数阶次的谐波。典型的后向CSE谐波辐射信号在参考文献[18]中被研究过:实验中,利用200nm厚的类金刚石薄膜(diamond-like carbon,DLC)与强度I≈4×1020W/cm2的激光脉冲相互作用,在透射方向上观察到25阶的低频“截止”阶次(相当于Ne≈625Nc),低于这个阶次的谐波强度受到很大的抑制,高于这个阶次的一定范围内,谐波强度随阶次升高的衰减比较缓慢。
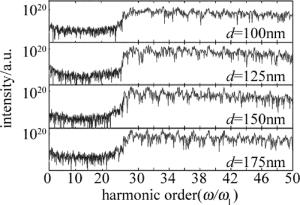
在较厚固体靶的情况下,反射方向的谐波主要来源于入射光场驱动固体靶表面电子的集体振荡对入射光的反射,从而使反射光场出现相位调制并包含高次谐波成分,即ROM过程。然而在超短强激光脉冲与厚度明显小于入射光波长的薄膜靶相互作用的情况中,由于表面电子的集体振荡可能会受到较小的固体靶厚度的影响而显著地影响反射方向的谐波辐射,因此在这种情况下,反射方向的谐波特征成为一个值得研究的问题。几种不同靶厚度情况下反射方向的谐波辐射如图 4所示。
在反射方向上,观察到有高次谐波的产生,而且谐波谱中都只包含奇数阶次的谐波成分。然而不同于透射方向的谐波特征对固体靶厚度的敏感性(厚度分别大于和小于200nm所呈现出的谐波谱有明显的区别),反射方向的整体谐波特征对固体靶厚度的依赖性较小。对于固体靶厚度小于200nm的情况,谐波特征的变化随固体靶厚度的改变不明显; 对于固体靶厚度小于200nm的情况,谐波阶次的变化随固体靶厚度的改变不明显,谐波阶次在大于25阶基本看不到明显的谐波峰。对于靶厚度增加到250nm情况,可以明显看到,谐波谱的阶次有所提升,谐波29以上阶次依然很明显。和透射方向的谐波辐射相比,反射方向上虽然低阶次的谐波强度高于透射方向的谐波强度,但是谐波强度随阶次增加,整体的衰减较快,而且所能达到的谐波阶次也远远低于透射方向的谐波分布。
在超短强激光脉冲与薄膜靶相互作用的过程中,反射方向上仍然能够观察到明显的谐波阶次,这说明即使是对于厚度较小的薄膜靶,对反射方向谐波起主要贡献的ROM机制仍然存在。而谐波谱的整体特征对固体靶厚度的依赖并不大,这一点也印证了ROM过程对反射方向谐波的贡献的存在性。因为在这种过程中,谐波源于表面电子的集体振荡对反射光相位的调制,在所研究的参量情况下,只要存在等离子体电子受入射脉冲的驱动而振荡,都能产生沿反射方向的谐波。因此在超短强激光脉冲与薄膜靶相互作用过程中,ROM谐波过程和CSE谐波过程共同存在,分别对反射方向和透射方向的谐波起着贡献。由于ROM谐波来源于集体振荡电子表面对入射光的反射,而CSE谐波来源于带电粒子辐射,后者所产生的高频谐波阶次及其强度都高于前者[19]。
-
(1) 在薄膜靶厚度小于激光趋肤深度和靶等离子体密度远大于临界密度的条件下,正入射超强激光驱动的CSE和ROM两种谐波产生机制共存,即在入射光的透射方向CSE机制起主导作用(CSE谐波)、在反射方向ROM机制起主导作用(ROM谐波)。
(2) 透射方向CSE谐波辐射的阶次对靶厚的依赖性强于反射方向ROM谐波辐射,增加靶厚(大于200nm、小于激光趋肤深度)有利于提高CSE和ROM谐波辐射的阶次。
(3) 对于低阶次谐波区,反射方向的ROM谐波辐射强度高于透射方向的CSE谐波辐射强度;但随谐波阶次升高,ROM谐波衰减较CSE谐波快,且所能达到的谐波阶次也低于透射方向的CSE谐波辐射。
超强激光驱动薄膜靶谐波辐射的模拟研究
Simulation study on harmonic radiation of ultraintense laser-driven thin foil targets
-
摘要: 为了研究超强激光与薄膜靶相互作用在入射光反射方向引起的高次谐波辐射,基于在入射激光的透射方向,相干同步辐射机制会导致高次谐波的产生,采用粒子模拟方法研究了超强激光驱动固体密度薄膜靶(即高密度薄膜靶)高次谐波辐射在入射激光透射和反射方向的空间分布。结果表明,当靶厚小于激光趋肤深度、靶等离子体密度远大于临界密度(800Nc)时,在透射方向,相干同步辐射机制会导致高次谐波辐射,同时在反射方向,存在相对论镜面振荡机制驱动的谐波场辐射,证明了在超强激光-薄膜靶相互作用过程中两种谐波会产生共存机制;讨论了在两种产生机制下,靶厚度对谐波辐射阶次的影响,发现靶厚度超过200nm,透射方向谐波阶次达到65阶以上。该研究对深入理解超强激光-薄膜靶驱动高次谐波的产生及阿秒X射线光源的未来发展具有一定的理论意义。Abstract: In order to study the higher order harmonic radiation induced by the interaction between super laser and thin foil targets in the reflection direction of incident light, the spatial distribution of high-order harmonic radiation of ultraintense laser-driven thin foil targets (high-density film targets) was investigated in the transmission and reflection direction of incident laser by using particle simulation method, because synchrotron radiation mechanism could lead to higher harmonic generation in the transmission direction of incident laser. The results show that, when the target thickness is less than the laser skin depth and the target plasma density is much larger than the critical density (800Nc), coherent synchrotron radiation can cause higher order radiation in the transmission direction. Harmonic field radiation is driven by relativistic mirror oscillation mechanism in the reflection direction. During the interaction between ultraintense laser and thin foil target, the coexistence of two harmonic generation mechanisms is proved. The influence of target thickness on the order of harmonic radiation was discussed under two kinds of production mechanism. The transmitted harmonics are more than 65 orders when target thickness exceeds 200nm. The study has some theoretical significance to research of high order harmonics generated by ultraintense laser-driven film targets and the future development of attosecond X-ray light sources.
-
Key words:
- laser physics /
- ultraintense laser /
- foil target /
- high-order harmonic
-
-
[1] NOMURA Y, HÖRLEIN R, TZALLAS P, et al. Attosecond phase locking of harmonics emitted from laser-produced plasmas[J]. Nature Physics, 2009, 5(2):124-128. doi: 10.1038/nphys1155 [2] LIU H, FENG L Q. Mid-infrared field phase measurement and attosecond pulse generation[J]. Laser Technology, 2017, 41(2):151-158(in Chinese). [3] FENG L Q, LIU H, LIU H.Spatial distribution of H2+ radiation harmonics in spatial homogeneous and inhomogeneous fields[J]. Laser Technology, 2017, 41(4):467-472(in Chinese). [4] BRUNEL F, BRUNEL F. Not-so-resonant, resonant absorption[J]. Physical Review Letters, 1987, 59(1):52-55. doi: 10.1103/PhysRevLett.59.52 [5] WIKS S C, KRUER W L, TABAK M, et al. Absorption of ultra-intense laser pulses[J]. Physical Review Letters, 1992, 69(9):1383-1386. doi: 10.1103/PhysRevLett.69.1383 [6] TEUBNER U, GIBBON P.High-order harmonics from laser-irradiated plasma surfaces[J]. Reviews of Modern Physics, 2009, 81(2):445-479. doi: 10.1103/RevModPhys.81.445 [7] BULANOV S V, NAUMOVA N M, PEGORARO F. Interaction of an ultrashort, relativistically strong laser pulse with an overdense plasma[J]. Physics of Plasmas, 1994, 1(3):745-757. doi: 10.1063/1.870766 [8] DROMEY B, ADAMS D, HÖRLEIN R, et al. Diffraction-limited performance and focusing of high harmonics from relativistic plasmas[J]. Nature Physics, 2009, 5(2):146-152. doi: 10.1038/nphys1158 [9] NOMURA Y, HÖRLEIN R, TZALLAS P, et al. Attosecond phase locking of harmonics emitted from laser-produced plasmas[J]. Nature Physics, 2009, 5(2):124-128. doi: 10.1038/nphys1155 [10] BAEVA T, GORDIENKO S, PUKHOV A. Theory of high-order harmonic generation in relativistic laser interaction with overdense plasma[J]. Physical Review, 2006, E74(4):046404. [11] DROMEY B, ZEPF M, GOPAL A, et al. High harmonic generation in the relativistic limit[J]. Nature Physics, 2006, 2(7):456-459. doi: 10.1038/nphys338 [12] BAKE M, AIMIDULA A.Proton acceleration of moving electric field driven by ultraintense laser pulse[J]. Laser Technology, 2017, 41(2):302-306(in Chinese). [13] HAO D Sh.A new accelerated mechanism of protons in high power laser-plasma[J]. Laser Technology, 2012, 36(5):653-656(in Chinese). [14] an der BRÜGGE D, PUKHOV A. Enhanced relativistic harmonics by electron nanobunching[J]. Physics of Plasmas, 2010, 17(3):033110. doi: 10.1063/1.3353050 [15] PUKHOV A, an der BRÜGGE D, KOSTYUKOV I. Relativistic laser plasmas for electron acceleration and short wavelength radiation generation[J]. Plasma Physics and Controlled Fusion, 2010, 52(12):124039. doi: 10.1088/0741-3335/52/12/124039 [16] SHUAI B, SHEN B F, LI R X, et al.High order harmonic generation in ultra thin plasma foil[J].Acta Optica Sinica, 2002, 22(10):1153-1158(in Chinese). [17] NIETER C, CARY J R. Vorpal:a versatile plasma simulation code[J]. Journal of Computational Physics, 2004, 196(2):448-473. [18] DROMEY B, RYKOVANOV S, YEUNG M, et al. Coherent synchrotron emission from electron nanobunches formed in relativistic laser-plasma interactions[J]. Nature Physics, 2012, 8(11):804-808. doi: 10.1038/nphys2439 [19] JACKSON J D, FOX R F. Classical electrodynamics[J]. American Journal of Physics, 1999, 67(9):841-842. -


 网站地图
网站地图

 下载:
下载: