网站地图
下载:
-
获得高功率、高光束质量的激光光束一直是激光领域探索的热点。光学非稳腔凭借其高的横模鉴别能力、可控的衍射输出耦合和大的模体积等优势，成为激光研究中获得高功率高光束质量激光光束的首选腔型[1-3]。但由于常规非稳腔输出光束通常为环形，光束的远场特性较差，聚焦后焦斑能量由中心向外逐步扩散，中心点的能量密度较低；另外，由于环形光束的遮拦比问题，相比同样功率(能量)密度的实心光束，需要更大口径的光学系统，增加了强激光系统中跟瞄、发射系统的制造成本及结构重量。这些缺陷严重限制了非稳腔激光器的实际推广应用。
为解决传统光学非稳腔环形光束输出带来的问题，国内外研究者提出了许多解决方案。ZUCKER等人[4]提出径向可变反射率非稳腔，采用逐步透射的输出方式消除“硬边”效应以达到基模运转。KUPRENYUK等人[5]提出了90°束转动激光器的概念。MINEEV等人[6]采用平板波导非稳腔改善光束质量。LUO等人[7-8]采用内外圆锥面反射镜相结合的方式设计了针对多模横流CO2激光器的环形光束整形系统。这些方案虽然解决了传统共焦腔环形输出的问题，但同时也引入了新的问题，如加工困难、调节复杂、功率低等限制因素[9]。
针对以上方案存在的问题及当前激光系统大口径、大能量的特点，结合近期一些新型的光束整形技术[10-11]，在综合考虑加工和装配可行性的基础上，设计了一种可以装配于激光腔外的基于双轴锥镜的透射式环形光束整形装置。
-
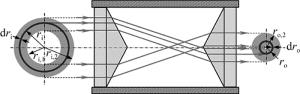
轴锥镜是一种很重要的光学器件，在各种需要特殊光束的领域具有重要的应用[12-20]。双轴锥镜环形光束整形装置由两个轴锥镜组成，如图 1所示。两个轴锥镜具有相同的锥顶角，其锥顶相对且同轴装配。由图 1可以看出，垂直于轴锥镜底面入射的光线分别经两个轴锥镜折射后，光线的出射方向与入射方向一致, 即该整形装置不改变光线的传输方向，而是将入射光线沿径向平移，使光束在保持传播方向不改变的前提下靠近光轴，将环形空心激光束转变为近似实心的激光束。对于沿光轴方向入射的平行平面波，该装置具有等光程特性，即输出光束仍旧为平面波。两轴锥镜之间的距离可以调节用以改变输出光束的直径。
Figure 1. Schematic diagram of annular laser beam reshaping based on dual axicons
对于沿光轴方向入射的平行平面波，设入射环形光束的内环半径为ri, 1，外环半径为ri, 2，经双轴锥镜整形后出射环形光束的内环半径为ro, 1，外环半径为ro, 2。在入射光束中取一半径为ri、厚度为dri的环形微元光束，对应的出射环形微元光束半径为ro，厚度为dro。由图 1的几何关系可以得到：
$ {r_{\rm{i}}} + {r_{\rm{o}}} = {r_{{\rm{i, }}1}} + {r_{{\rm{o, 2}}}} = {r_{{\rm{i, 2}}}} + {r_{{\rm{o, 1}}}} $
(1) $ {\rm{d}}{r_{\rm{o}}} = {\rm{d}}{r_{\rm{i}}} $
(2) 设入射光束为均匀分布的轴对称环形光束，其振幅为E0，则半径ri对应的入射面光场相对分布为Ei(ri)：
$ {E_{\rm{i}}}({r_{\rm{i}}}) = \left\{ \begin{array}{l} {E_{\rm{0}}}, ({r_{{\rm{i, 1}}}} < {r_{\rm{i}}} < {r_{{\rm{i, 2}}}})\\ 0, \left( {{\rm{other}}} \right) \end{array} \right. $
(3) 设出射光场分布为Eo(ro)，忽略双轴锥镜对光的衰减，根据能量守恒原则，有：
$ {\left| {{E_{\rm{o}}}({r_{\rm{o}}})} \right|^2}{r_{\rm{o}}}{\rm{d}}{r_{\rm{o}}} = {\left| {{E_{\rm{i}}}({r_{\rm{i}}})} \right|^2}{r_{\rm{i}}}{\rm{d}}{r_{\rm{i}}} $
(4) 根据(1)式~(4)式可得：
$ \left| {{E_{\rm{o}}}({r_{\rm{o}}}){\rm{ }}} \right| = \left\{ \begin{array}{l} {E_0}\sqrt {\frac{{{\mathit{r}_{{\rm{o, 1}}}} + {\mathit{r}_{{\rm{i, 2}}}}}}{{{r_{\rm{o}}}}} - 1} , ({r_{{\rm{o}}, 1}} < {r_{\rm{o}}} < {r_{{\rm{o}}, 2}})\\ 0, \left( {{\rm{other}}} \right) \end{array} \right. $
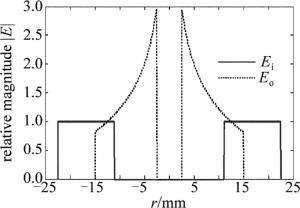
(5) 图 2描述了平顶环形光束经双轴锥镜装置变换前后的光场分布。由图中可以看出，在ro, 2 < ri, 2时，双轴锥镜整形装置通过对光束的径向平移变换，在不改变光束传输方向和发散角的前提下，实现了光束能量向光轴的集中分布。
Figure 2. Beam field distribution of flat annular beams before and after shaping by dual axicons
实际的非稳腔激光束并非平面波，但在靠近束腰处，瑞利长度范围内，其波面可近似为平面。双轴锥镜整形装置的长度远小于激光器出射光的瑞利长度，因此，在理论分析时，可以将其光束作为平面波处理。
-
为了验证双轴锥镜对环形激光束的整形效果，利用自行加工装配的双轴锥镜光束整形装置进行了实验。两个轴锥镜由K9玻璃加工而成，口径60mm，锥角120°，表面镀1.06μm增透膜。两个轴锥镜锥尖相对装配在一个铝合金镜筒中保持同轴，其间距可根据光束整形需求进行调节。系统有效通光口径为56mm。
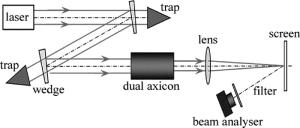
实验光路如图 3所示。所采用的激光器为非稳腔高能激光器。激光器输出的环形光束经光楔两次反射衰减至较低的能量，经双轴锥镜装置整形后输出，照射到反射屏上形成光斑。在双轴锥镜装置后方加入透镜可以将光束聚焦至反射屏上形成会聚光斑。透镜焦距为5m。采用Spiricon的SP620U光束分析仪对经过双轴锥镜装置整形的激光束进行分析。光束分析仪采集反射屏上的光斑，测量光斑参量。
Figure 3. Schematic diagram of beam reshaping experiment
实验结果如图 4和图 5所示。图 4为没有加入透镜时，激光器在不同放电电压下，输出的光束经过双轴锥镜装置整形前后的光斑分布。图 4a和图 4b为没有经过整形的原始激光束光斑分布；图 4c和图 4d为经过双轴锥镜装置整形的激光束光斑分布。由图中可以看出，经过整形后，光斑中心空心区域减小，光斑直径减小，光斑能量分布更加集中，能量密度增大。实验中采用功率通量法作为评价光束质量的标准。由光束分析仪测得的原始光斑直径为45mm，变换后光斑直径为32mm。
图 4 Intensity distribution of beam before and after reshaping by dual axicons
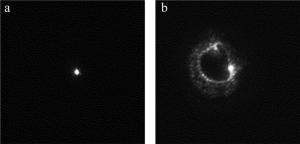
Figure 5. Intensity distribution of the converged beam before and after reshaping by dual axicon a—original beam b—transformed beam
图 5为经过5m焦距透镜会聚的激光束在反射屏上的光斑分布图像。原始光束会聚光斑直径为2.1mm，经过双轴锥镜变换后会聚的光斑直径为2.5mm。由此可以得到基于功率通量法的光束远场发散角θ：
$ \theta = \frac{d}{f} $
(6) 式中，d为会聚光斑直径，f为透镜焦距。得到原始光束远场发散角为0.42mrad，变换后光束远场发散角为0.5mrad。
由实验数据可以计算出基于功率通量法的光束质量因子：
$ {M^2} = \frac{{w\left( 0 \right)\theta }}{{4\lambda /{\rm{ \mathsf{ π} }}}} $
(7) 式中，w(0)为基于功率通量法得到的光束在束腰处的直径，原始束腰直径为45mm，变换后束腰直径为32mm。计算得到变换前后的光束质量因子M2分别为14和11.8。
-
通过对双轴锥镜光束整形方法进行理论分析，证明了其用于光学非稳腔输出环形光束整形变换的可行性。设计加工了基于双轴锥镜的光束整形装置，针对当前可用的非稳腔高能激光器输出的环形光束进行了整形实验。结果表明，采用双轴锥镜装置整形后，输出环形光束的遮拦比减小，光束的能量分布向光轴集中，光束束腰直径由45mm减小为32mm，而其远场发散角由0.42mrad增大为0.5mrad，光束质量因子M2由14减小到11.8。因此，变换后的光束比原始环形光束具有更好的光束质量。
基于双轴锥镜的环形激光束整形
Annular laser beam reshaping based on dual axicons
-
摘要: 为了改善非稳腔高能激光系统的光束质量，提高发射光学系统口径的利用率，采用新型的可用于光学非稳腔输出环形光束的光学整形方法，通过在激光腔外的光路上增加光学元件对输出的环形激光束进行了整形变换。在理论分析的基础上，设计并加工了基于双轴锥镜的光束整形装置，针对非稳腔高能激光器输出的环形光束进行了整形实验，取得了与理论分析一致的数据。结果表明，采用双轴锥镜装置整形后的光束比原始光束具有更好的光束质量，光束束腰直径由45mm减小为32mm，光束质量因子M2由14减小到11.8。该方法用于光学非稳腔输出环形光束整形变换具有可行性。Abstract: In order to improvelaser beam quality of unstable cavity high energy laser systems and the utilization of the aperture of a transmitting optical system, a new optical shaping method for the annular beam was proposed. Optical elements were added to the light path outside the laser cavity to shape the output of annular laser beam. On the basis of theoretical analysis, beam shaping devices based on dual axicons were designed and fabricated. The shaping experiments were carried out for the annular beam from an unstable cavity high energy laser. The data was obtained and was consistent with theoretical analysis.The results show that, the beam after shaping by using dual axicons has better beam quality than that of the original beam. Waist diameter decreases from 45mm to 32mm. M2 factor reduces from 14 to 11.8. The method is feasible for the shaping and transformation of the annular beam from an unstable resonator.
-
Key words:
- laser optics /
- annular beam /
- beam reshaping /
- axicon
-
Figure 2. Beam field distribution of flat annular beams before and after shaping by dual axicons
-
[1] SEIGMAN A E. Unstable optical resonators for laser applications[J]. Proceeding of the IEEE, 1965, 53(3):277-287. doi: 10.1109/PROC.1965.3685 [2] SEIGMAN A E. Modes in unstable resonators and lens waveguides[J]. IEEE Journal of Quantum Electronics, 1967, 3(4):156-163. doi: 10.1109/JQE.1967.1074471 [3] SEIGMAN A E. Unstable optical resonators[J]. Applied Optics, 1974, 13(2):353-367. doi: 10.1364/AO.13.000353 [4] ZUCKER H. Optical resonators with variable reflectivity mirrors[J]. Bell System Technical Journal, 1970, 49(9):2349-2376. doi: 10.1002/bltj.1970.49.issue-9 [5] KUPRENYUK V N, SEMENOV V E, SMIRNOVA L D. Wave-approximation calculation ofan unstable resonator with field rotation[J]. IEEE Soviet Journal of Quantum Electronics, 1983, 13(12):1613-1617. doi: 10.1070/QE1983v013n12ABEH005007 [6] MINEEV A P, NEFEDOV S M, PASHININ P P, et al. RF excited planar CO2 laser with hybrid waveguide-unstable resonator cavities[J]. Proceedings of the SPIE, 1999, 3638:35-42. doi: 10.1117/12.342817 [7] LUO X. Investigation on the propagation and transformation and beam control of high-power lasers[D]. Wuhan: Huazhong University of Science and Technology, 2011: 57-78(in Chinese). [8] LIU Zh X. Research to the reconstruction approach for central dark region of annular-beam output of optical unstable resonator[D]. Wuhan: Huazhong University of Science and Technology, 2013: 22-25(in Chinese). [9] ZIZZO C, ARNONE C, CALI C, et al. Fabrication and characterization of tuned Gaussian mirror for the visible and the near infrared[J]. Optics Letters, 1988, 13(5):342-344. doi: 10.1364/OL.13.000342 [10] LOU Y Y, ZHENG X L, ZHANG Sh C, et al. Flat-top beams spatial shaping with digital micromirror device[J]. Laser Technology, 2016, 40(6):916-920(in Chinese). [11] SANJIV K T, SATYA R M, SURJYA P R. Generation of a variable-diameter collimated hollowlaser beam using metal axicon mirrors[J]. Optical Engineering, 2011, 50(1):014001. doi: 10.1117/1.3530080 [12] WU Zh W. Bottle beam with adjustable size generated by a frustum and axicon system[J]. Laser Technology, 2014, 38(5):655-659(in Chinese). [13] LI Sh M, WANG Y, HU A J, et al. A method of forming annular pump light[J]. Laser Technology, 2015, 39(5):621-624(in Chinese). [14] WEI M D, SHIAO W L, LIN Y T. Adjustable generation of bottle and hollow beams using an axicon[J]. Optics Communications, 2005, 248(1/3):7-14. [15] XIE Z, ARMBRUSTER V, GROSJEAN T. Axicon on a gradient index lens (AXIGRIN):integrated optical bench for Bessel beam generation from a point-like source[J]. Applied Optics, 2014, 53(26):6103-6106. doi: 10.1364/AO.53.006103 [16] JENS B, MATTHIAS C W, ULRIKE W. Fast and robust piezoelectric axicon mirror[J]. Optics Letters, 2014, 39(15):4631-4634. doi: 10.1364/OL.39.004631 [17] GOLUB I, CHEBBI B, SHAW D, et al. Characterization of a refractive logarithmic axicon[J]. Optics Letters, 2010, 35(16):2828-2830. doi: 10.1364/OL.35.002828 [18] CHEBBI B, GOLUB I, BREYGIN P. Characterization of a refractive linear axicon with distant depth of field and no central blocking[J]. Applied Optics, 2013, 52(35):8572-8575. doi: 10.1364/AO.52.008572 [19] WOJNOWSKI D, JANKOWSKA E, MASAJADA J, et al. Surface profilometry with binary axicon-vortex and lens-vortex optical elements[J]. Optics Letters, 2014, 39(1):119-122. doi: 10.1364/OL.39.000119 [20] BRUNNE J, WAPLER M C, WALLRABE U. Fast and robust piezoelectric axicon mirror[J]. Optics Letters, 2014, 39(15):4631-4634. doi: 10.1364/OL.39.004631 -
点击查看大图
图(5)
计量
- 文章访问数: 7758
- HTML全文浏览量: 5132
- PDF下载量: 258
- 被引次数: 0
