网站地图
-
聚焦是显微镜成像系统的重要环节，常用的聚焦方法主要分为焦点检测法、测距法和图像处理法3种[1]。相比于焦点检测法和测距法，基于数字图像处理的自动聚焦技术具有智能化、快速准确、控制方便等特点，成为近年来研究的热点[2-3]。其中，聚焦评价函数的选取是基于数字图像处理的自动聚焦技术的核心问题之一，它直接决定聚焦的准确性。目前已有的聚焦评价函数主要分为3类：频域类函数、梯度类函数和统计类函数[4-5]。在光照强度适宜的条件下，显微镜采集的图像对比度高，细节更明显，上述的聚焦评价函数均能满足聚焦的要求；但遇到光照强度较弱的条件下，上述的聚焦评价函数大多会失去原来的理想曲线特性，造成聚焦的不准确性。低照度的显微图像，对比度低、噪声大、图像整体和细节辨识度较低，加大聚焦的难度。虽然可以通过提升对比度、低通滤波器等方式减弱光强对聚焦的影响，但图像方法拉伸对比度也会增加额外的噪声、低通滤波器的选择不当也会造成滤波不足使得噪声依然存在或者滤波过度使得原本有用的高频信息被消除的问题[6]。
大多数传统聚焦评价函数不能克服光照变化带来的不利影响，针对此问题，本文中提出一种基于离散余弦变换(discrete cosine transform，DCT)零系数和局部标准差的聚焦算法，该算法结合频域DCT零系数和空域局部标准差，在光照变化的条件下，还能保持良好的聚焦特性，适用于显微镜成像系统。
-
实现高精度的自动聚焦是显微镜自动化的首要问题之一[7]，其关键是确定评价聚焦评价函数的定性指标。一个理想的聚焦评价函数应满足单峰性、无偏性、高灵敏性和抗噪性[8]。
-
本节中列举的5种聚焦函数用于后续的对比实验，其中F为聚焦评价函数值，f(x, y)为图像点(x, y)的灰度值，图像大小为M×N。
(1) 灰度差分绝对值和(sum modulus difference，SMD)函数[9] :
$ \begin{array}{*{20}{c}} {{F_{{\rm{SMD}}}} = \sum\limits_{x = 1}^M {\sum\limits_{y = 1}^N {\left[ {\left| {f\left( {x,y} \right) - f\left( {x,y - 1} \right)} \right| + } \right.} } }\\ {\left. {\left| {f\left( {x,y} \right) - f\left( {x - 1,y} \right)} \right|} \right]} \end{array} $
(1) (2) 方差函数[10](variance函数):
$ \left\{ \begin{array}{l} {F_{{\rm{variance}}}} = \sum\limits_{x = 1}^M {\sum\limits_{y = 1}^N {{{\left[ {\left| {f\left( {x,y} \right) - {{\bar f}_1}} \right.} \right]}^2}} } \\ {{\bar f}_1} = \frac{1}{{MN}}\sum\limits_{x = 1}^M {\sum\limits_{y = 1}^N {f\left( {x,y} \right)} } \end{array} \right. $
(2) 式中, f1为图像的灰度平均值。
(3) 基于Robert算子的差分绝对值和函数[11](简称Robert函数):
$ \begin{array}{*{20}{c}} {{F_{{\rm{Robert}}}} = \sum\limits_{x = 1}^M {\sum\limits_{y = 1}^N {\left[ {\left| {f\left( {x,y} \right) - f\left( {x + 1,y + 1} \right)} \right| + } \right.} } }\\ {\left. {\left| {f\left( {x,y} \right) - f\left( {x,y + 1} \right)} \right|} \right]} \end{array} $
(3) (4) 基于Sobel算子的函数[12](简称Sobel函数):
$ \left\{ \begin{array}{l} {F_{{\rm{Sobel}}}} = \sum\limits_{x = 1}^M {\sum\limits_{y = 1}^N {\left[ {\left| {{g_x}\left( {x,y} \right)} \right| + \left| {{g_y}\left( {x,y} \right)} \right|} \right]} } \\ {\mathit{\boldsymbol{S}}_x} = \left[ {\begin{array}{*{20}{c}} { - 1}&0&1\\ { - 2}&0&2\\ { - 1}&0&1 \end{array}} \right],{\mathit{\boldsymbol{S}}_y} = \left[ {\begin{array}{*{20}{c}} { - 1}&{ - 2}&{ - 1}\\ 0&0&0\\ 1&2&1 \end{array}} \right] \end{array} \right. $
(4) 式中, gx(x, y)和gy(x, y)分别表示图像与水平和垂直Sobel算子Sx和Sy的卷积。
(5) 离散傅里叶变换(discrete Fourier transform，DFT)函数[13]:
$ \left\{ \begin{array}{l} \mathit{\boldsymbol{f}}\left( {u,v} \right) = \sum\limits_{u = 1}^M {\sum\limits_{v = 1}^N {f\left( {x,y} \right)\exp \left( {\frac{{ - {\rm{j}}2{\rm{ \mathsf{ π} }}xu}}{M}} \right)} } \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left( {\frac{{ - {\rm{j}}2{\rm{ \mathsf{ π} }}yv}}{N}} \right)\\ {F_{{\rm{DFT}}}} = \sum\limits_{u = 1}^M {\sum\limits_{v = 1}^N {\left| {\mathit{\boldsymbol{f}}\left( {u,v} \right)} \right|} } \end{array} \right. $
(5) 式中, f(u, v)为图像进行离散傅里叶变换后的频率系数矩阵。
-
评价聚焦评价函数性能的好坏，除了定性指标(单峰性、无偏性、高灵敏度和抗噪性)还应结合定量指标，定量指标更能客观地体现不同聚焦评价函数的差异。
(1) 清晰度比率R
清晰度比率R表征聚焦评价函数对不同离焦程度图像的分辨能力[12]。R越大，聚焦图像和离焦图像清晰度值的差异越大，越容易区分。
$ R = \frac{{{F_{\max }}}}{{{F_{\min }}}} $
(6) 式中, Fmax和Fmin聚焦函数的最大值和最小值(最小值应在聚焦曲线的平缓区取得)。
(2) 灵敏度因子S
灵敏度因子S表征聚焦评价函数最大值附近变化的剧烈程度[12]。对于不同的聚焦评价函数，灵敏度因子越高，则该函数适用于细聚焦阶段。
$ S = \frac{{{F_{\max }} - F\left( {{x_{\max }} + {x_1}} \right)}}{{F\left( {{x_{\max }} + {x_1}} \right)}} $
(7) 式中，x1为横坐标变化量，xmax为函数最大值的横坐标。
(3) 平缓区波动量V
受噪声的影响，平缓区的聚焦评价函数值并不是单调递增或递减，而是呈现出一种波动状态[14]，波动越平缓，说明该函数的抗噪性较强。首先假设采样点有N个(曲线的平缓区取得)，则定义N个点的函数值标准差为平缓区波动量。
$ V = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {\left[ {F\left( i \right) - {{\bar f}_2}} \right]} } $
(8) 式中, F(i)为采样点i所对应的聚焦函数值，f2为平缓区的灰度均值。
-
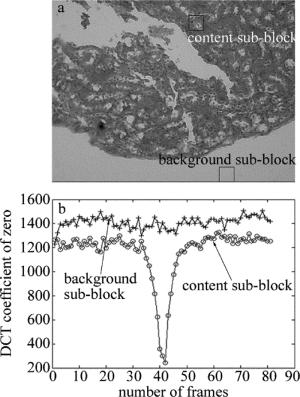
图像经过DCT变换后的DCT系数矩阵体现了图像频率的分布情况。对于任意的图像进行DCT变换，得到一个2维矩阵F1(u, v)，随着u和v的增大，对应的DCT系数也不断增大。DCT系数主要分为低频系数、中频系数和高频系数3种。在图像局部模糊检测中，由于模糊区域边缘信息较少，导致高频系数为零的个数较多；而内容丰富的清晰区域，高频零系数个数较少[15]。在此理论基础上，可以发现在聚焦的过程中，内容子块经历了模糊→清晰→模糊这样一个过程，其对应的高频零系数的个数发生相应的变化。而背景子块在聚焦过程基本上无变化，故其对应的高频零系数个数基本上不变。
选中的图像子块位置如图 1a所示，图 1b为相同位置的子块在聚焦过程中DCT零系数个数的变化曲线图。从图 1b中可以看出，内容子块的DCT零系数在聚焦位置个数最少，且曲线变化和理想的聚焦评价函数曲线有相同的特性，但唯一的区别是，曲线最小值点为图像聚焦位置。背景子块的DCT零系数个数在一定的范围内波动，且内容子块的DCT零系数个数变化曲线的平缓区也出现一定的波动，这是受图像子块中噪声的影响，引起误判造成的，但不影响后续算法中应用。
Figure 1. a—the positions of sub-blocks b—the curves of DCT coefficient of zero of the sub-blocks
图 1b中，内容子块的DCT零系数个数变化明显，而背景子块的DCT零系数个数则在一定的范围内波动，故图像所有子块的DCT零系数个数相加之和，可作为聚焦评价函数，其最小值点即为聚焦位置。
-
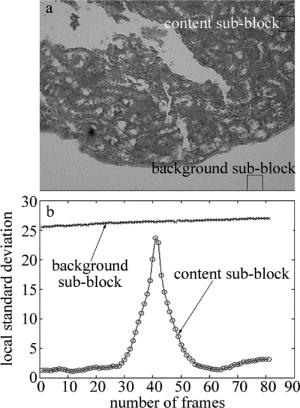
局部标准差反映图像局部灰度值的变化程度[16]。在图像局部模糊检测中，一般用于单个像素点的判断。图像分为模糊区域和清晰区域，模糊区域包含较少的边缘信息，灰度变化缓慢，故局部标准差较小；而清晰区域包含较多的边缘信息，灰度变化剧烈，一般具有较大的局部标准差。同样的道理，在聚焦的过程中，内容子块经过了模糊→清晰→模糊的过程，故可以推断，在此过程中，内容子块的局部标准差也发生相应的变化，且在聚焦位置内容子块的局部标准差最大。而背景子块灰度值基本不变[17], 故背景子块的局部标准差也基本不变。
选中的图像子块位置如图 2a所示，图 2b为相同位置的子块在聚焦过程中局部标准差的变化曲线。从图 2可以看出，在聚焦的过程中，内容子块的局部标准差变化剧烈，最清晰图片对应的位置为曲线最大值处，满足聚焦曲线的特性。而背景子块的局部标准差在一定的范围内基本不变，故图像所有子块的局部标准差之和也可作为聚焦评价函数，其曲线最大值点即为聚焦位置。
Figure 2. a—the positions of sub-blocks b—the curves of local standard deviation of the sub-blocks
-
对大小为M×N的图像进行分块，将其划分为m×n个图像块，子块大小为w×w，其中m=M/w，n=N/w。(i, j)为图像子块位置，f(x, y)为图像点(x, y)的灰度值。
(1) 对图像子块进行DCT变换:
$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_2}\left( {u,v} \right) = c\left( u \right)c\left( v \right) \times }\\ {\sum\limits_{u = 0}^{w - 1} {\sum\limits_{v = 0}^{w - 1} {\cos \left[ {\frac{{\left( {2w + 1} \right)u{\rm{ \mathsf{ π} }}}}{{2w}}} \right]\cos \left[ {\frac{{\left( {2w + 1} \right)v{\rm{ \mathsf{ π} }}}}{{2w}}} \right]} } } \end{array} $
(9) 式中,
$ \left\{ \begin{array}{l} c\left( u \right) = \left\{ \begin{array}{l} \sqrt {1/w} ,\left( {u = 0} \right)\\ \sqrt {2/w} ,\left( {1 \le u \le w - 1} \right) \end{array} \right.\\ c\left( v \right) = \left\{ \begin{array}{l} \sqrt {1/w} ,\left( {v = 0} \right)\\ \sqrt {2/w} ,\left( {1 \le v \le w - 1} \right) \end{array} \right. \end{array} \right. $
(10) (2) 统计子块(i, j)内DCT零系数个数:
$ d\left( {i,j} \right) = \left\{ \begin{array}{l} d\left( {i,j} \right) + 1,\left( {{\mathit{\boldsymbol{F}}_2}\left( {u,v} \right) = 0} \right)\\ d\left( {i,j} \right),\left( {{\rm{else}}} \right) \end{array} \right. $
(11) (3) 求子块(i, j)的局部标准差:
$ \sigma \left( {i,j} \right) = \sqrt {\frac{1}{{{w^2}}}\sum\limits_{x = 1}^w {\sum\limits_{y = 1}^w {{{\left[ {f\left( {x,y} \right) - {{\bar f}_3}} \right]}^2}} } } $
(12) 式中, f3为图像子块的灰度均值。
(4) 在聚焦的过程中，图像子块的DCT系数个数和局部标准差发生剧烈的变化，DCT零系数个数与局部标准差的变化正好相反，利用这个特性，组建新的聚焦函数，并进行平方运算来加大函数的清晰度比率，公式如下：
$ F = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{{\left[ {\frac{{\sigma \left( {i,j} \right)}}{{d\left( {i,j} \right)}}} \right]}^2}} } $
(13) 在聚焦的过程中，子块的DCT零系数个数变化如图 1b所示，而子块的局部标准差的变化如图 2b所示，当图像最清晰时(最佳聚焦点)，此时相同位置的内容子块的d(i, j)最小，σ(i, j)最大，则其对应的F最大；而相同位置的背景子块的d(i, j)和σ(i, j)则在一定范围内保持不变，则其对应的F在一定的范围内平缓波动，故所有子块的聚焦函数值F在图像最清晰的情况下，处于最大值位置，符合聚焦函数曲线的特性，且聚焦的过程中，d(i, j)和σ(i, j)的作用效果相反，相除会使得函数作用效果更加明显，更能区分离焦图像和聚焦图像的差异。在此过程中，背景子块一直在一定的范围内波动，作用不大，起决定性作用的是内容子块，故一般先确定聚焦窗口，剔除背景子块，使得聚焦效果更明显。而本文中聚焦函数不仅能适用于对整幅图像进行处理，且也具有理想聚焦曲线的一般特性。
-
本文中的实验坏境为：CPU，Intel(R) Core(TM)i7-6700 3.4GHz；RAM，8.00GB；MATLAB(R2014a)。
实验图片(480×640)均通过梧州奥卡光学仪器公司研发的光学显微镜(XSZ-8100)进行采集。
-
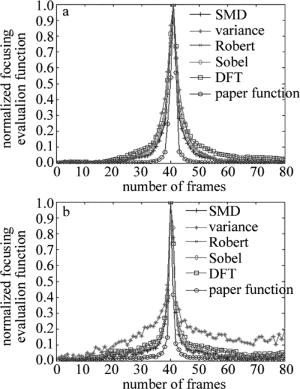
验证本文中函数的性能，对所提到的聚焦函数进行仿真实验。实验中采用如图 3、图 4所示的2组不同光照强度但内容相同的显微图像序列(离焦-聚焦-离焦)。为了便于观察，图像序列的最佳聚焦位置为第40帧。聚焦窗口的选取方法统一使用参考文献[18]中提到的选取方法。
Figure 3. Defocus and focus images with light intensity of 6
Figure 4. Defocus and focus images with light intensity of 1
实验仿真曲线如图 5所示。从图 5a可以看出，本文中聚焦评价函数和传统的聚焦评价函数在光照稳定的条件下，均满足单峰性和无偏性。当光照强度较弱的情况下，显微图像序列的噪声大，图像整体和细节辨识度较低。从图 5b中可以看出，在低照度的情况下，传统聚焦评价函数的仿真曲线大多数出现了局部极值，且平缓区出现了波动，而本文中函数还能保持理想曲线的特性。故本文中函数适用于低照度的自动聚焦系统，且具有较强的抗噪性。
Figure 5. Simulation curves of focusing function
-
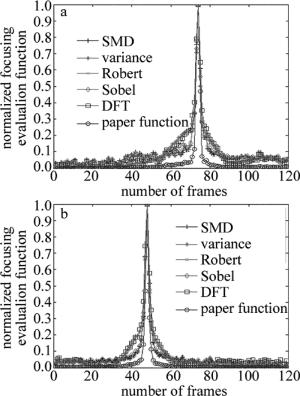
为了进一步验证本文中函数的适用性，通过与传统的聚焦函数进行再次聚焦对比实验，实验中采用2组低照度的显微图像序列(离焦-聚焦-离焦)如图 6、图 7所示。聚焦窗口的选取方法统一使用参考文献[18]中所提到的选取方法。图 6所示的图像序列的最佳聚焦位置在第74帧，图 7所示的图像序列的最佳聚焦位置在第48帧。
Figure 6. Defocus and focus images with light intensity of 1.5
Figure 7. Defocus and focus images with light intensity of 2
此处需要说明是：(1)光照强度越弱，采集到的显微图像序列整体灰度值越低，对比度越低，且噪声越大，对聚焦评价函数的影响也就越大，但由于光照强度低于1的情况下，即使能从肉眼能辨别图片的聚焦位置，但本文中函数与传统聚焦函数曲线均失去理想的曲线特性，故实验中选取光照强度大于1的图像序列; (2)考虑到选用低通滤波器不当有可能造成噪声依然存在或滤除掉图像的有用信息，造成聚焦的不准确，故不对图像进行预处理; (3)对图片不进行预处理噪声依然存在，在实验的过程中，以此来判断聚焦评价函数的抗噪能力。实验仿真曲线如图 8所示。
Figure 8. Simulation curves of focusing function
-
从实验仿真曲线可以看出，本文中函数在低照度的情况下还能满足理想聚焦曲线的特性，而传统的聚焦评价函数在低照度的情况下，由于受噪声的影响，平缓区出现波动，且随着光照强度的增加，平缓区波动也逐渐平缓。
对进行实验的聚焦函数进行定量分析。通过数据分析各函数的曲线特性。表 1、表 2中给出实验2中，各函数的清晰度比率R、灵敏度因子S、平缓区波动量V和处理时间t。
Table 1. Performance index of each focusing function with light intensity of 1.5
R S V t/s SMD 13.8044 0.5673 0.0269 1.326142 variance 78.4480 0.9654 0.0302 1.322258 Robert 12.6970 0.5820 0.0258 1.313597 Sobel 13.5474 0.6868 0.0247 1.328389 DFT 2.54260 0.2707 0.0243 1.329700 function 836.6905 1.1225 0.0047 1.379609 Table 2. Performance index of each focusing function with light intensity of 2
R S V t/s SMD 22.4191 0.8646 0.0105 1.314081 variance 67.4118 1.1480 0.0320 1.291682 Robert 19.9621 0.9036 0.0098 1.297270 Sobel 20.9368 1.0013 0.0144 1.287387 DFT 2.5740 0.3500 0.0388 1.304584 function 770.5649 2.2784 0.0044 1.350446 从表 1、表 2可以看出，在低照度的条件下，本文中聚焦评价函数的清晰度比率远远大于传统的聚焦函数，证明该函数对于不同程度的离焦图像具有较强的分辨力，同时也说明了本文中函数具有较强的抗噪性。而本文中聚焦评价函数的灵敏度因子提高了0.1571~1.9284，相比传统的聚焦评价函数，该函数的灵敏度因子至少提高了16.3%，说明该函数具有较高的灵敏度，且在函数最大值附近变化剧烈，适用于精聚焦阶段。平缓区波动量的大小，表征一个函数的抗噪性能强弱，而本文中聚焦评价函数的平缓区波动量最小，该函数的平缓区波动量减少了0.0054~0.0344，相比于传统的聚焦评价函数，该函数的平缓区波动至少减少了55.1%，说明该函数抗噪性强，且具有较强的稳定性。
从时间上来看，本文中函数的耗时和传统的聚焦函数相差不多。主要是因为本文中函数在计算的过程中有转换到频域，一般频域类函数计算复杂且计算量大，但在验证的过程中，利用参考文献[18]中的方法先确定了聚焦窗口，大大减少了计算量，且计算DCT高频零系数个数只是简单地对图像块计算零系数数目，故在耗时上稍慢于传统的聚焦函数。
-
聚焦评价函数是显微镜自动聚焦系统的重要环节，通过分析聚焦评价函数的理想曲线特性，本文中提出一种基于频域DCT零系数和空域局部标准差的自动聚焦算法，该算法在光照强度适宜的条件下，与传统的聚焦函数均能保持良好的聚焦特性，但在光照强度较弱的情况下，大多数传统聚焦函数会失去理想的曲线特性，容易造成聚焦的不准确。而本文中函数在低照度的情况下，还能保持良好的曲线特性，且在灵敏度、抗噪性和稳定性方面具有一定的优势。综上所述，本文中函数适用于显微镜自动聚焦系统。
基于DCT零系数和局部标准差的自动聚焦算法
Automatic focusing algorithm based on DCT coefficient of zero and local standard deviation
-
摘要: 聚焦评价函数的设计与选取是显微镜自动聚焦的核心问题之一，光照变化引起函数曲线失去理想特性，传统的聚焦评价函数无法克服这一问题。为了解决此问题，提出一种结合频域离散余弦变换（DCT）零系数和空域局部标准差的自动聚焦算法。通过计算图像子块的DCT高频零系数个数和局部标准差，利用两者相反的作用效果进行除法运算，并采用平方运算加大该算法的清晰度比率，在不同光照条件下，与几种传统的聚焦评价函数进行聚焦对比实验，验证了该算法的适用性，并对聚焦评价函数使用定量指标进行性能评估。结果表明，该算法在低照度的条件下还能保持良好的曲线特性，并且具有较强的抗噪性、灵敏度和稳定性。Abstract: The design and selection of focusing evaluation function was one of the key problems of automatic focusing microscopes. The illumination change would cause function curve to lose its ideal characteristics. The traditional focusing evaluation function can not overcome this problem. In order to solve the problem, an automatic focusing algorithm combining discrete cosine transform (DCT) coefficient of zero of frequency domain and local standard deviation of spatial domain was proposed. DCT coefficient of zero and local standard deviation of sub-blocks were calculated. Division operation was performed by taking advantage of the opposite effect. And square algorithm was used to increase the clarity ratio of the algorithm. Under different light conditions, compared with several traditional focusing evaluation functions, the focusing experiment was carried out to verify the applicability of the new algorithm. The performance of focus evaluation function was evaluated quantitatively. The results show that the algorithm can keep good curve characteristics under low illumination conditions and has strong anti-noise ability, sensitivity and stability.
-
Figure 1. a—the positions of sub-blocks b—the curves of DCT coefficient of zero of the sub-blocks
Figure 2. a—the positions of sub-blocks b—the curves of local standard deviation of the sub-blocks
Figure 3. Defocus and focus images with light intensity of 6
a—defocus image b—focus image
Figure 4. Defocus and focus images with light intensity of 1
a—defocus image b—focus image
Figure 5. Simulation curves of focusing function
a—with light intensity of 6 b—with light intensity of 1
Figure 6. Defocus and focus images with light intensity of 1.5
a—defocus image b—focus image
Figure 7. Defocus and focus images with light intensity of 2
a—defocus image b—focus image
Figure 8. Simulation curves of focusing function
a—with light intensity of 1.5 b—with light intensity of 2
Table 1. Performance index of each focusing function with light intensity of 1.5
R S V t/s SMD 13.8044 0.5673 0.0269 1.326142 variance 78.4480 0.9654 0.0302 1.322258 Robert 12.6970 0.5820 0.0258 1.313597 Sobel 13.5474 0.6868 0.0247 1.328389 DFT 2.54260 0.2707 0.0243 1.329700 function 836.6905 1.1225 0.0047 1.379609 
下载: 导出CSV
Table 2. Performance index of each focusing function with light intensity of 2
R S V t/s SMD 22.4191 0.8646 0.0105 1.314081 variance 67.4118 1.1480 0.0320 1.291682 Robert 19.9621 0.9036 0.0098 1.297270 Sobel 20.9368 1.0013 0.0144 1.287387 DFT 2.5740 0.3500 0.0388 1.304584 function 770.5649 2.2784 0.0044 1.350446
下载: 导出CSV
-
[1] ZOU Ch F, LIU B Q, HUANG F Y, et al. Automatic focusing evaluation function based on multi-directional maximal gradient threshold method[J]. Laser & Infrared, 2016, 46(1):115-118(in Chinese). [2] ZHANG L X, SUN H Y, GUO H Ch, et al. Auto focusing algorithm based on largest gray gradient summation[J]. Acta Photonica Sinica, 2013, 42(5):605-610(in Chinese). doi: 10.3788/gzxb [3] LIU P, WANG Ch P, FU Q, et al. Auto-focusing method based on octahedral gradient variance for tracking system[J]. Video Engineering, 2013, 37(9):183-186(in Chinese). [4] MO Ch H, LIU B, DING L, et al. A gradient threshold auto-focus algorithm[J]. Infrared and Laser Engineering, 2014, 43(1):323-327(in Chinese). [5] JIN X, MA W H. Study on image definition evaluation function in auto-focusing process[J]. Optical Instruments, 2012, 34(1):59-64(in Chinese). [6] HAN R Y, WANG J J, NIE K, et al. Adaptive autofocus technique under different contrast[J]. Acta Photonica Sinica, 2012, 41(2):222-227(in Chinese). doi: 10.3788/gzxb [7] WANG Q, SONG E M, XU X Y, et al. Auto-focusing function for microscope image based on weighted neighborhood correlation[J]. Optics and Precision Engineering, 2008, 16(1):166-171(in Chinese). [8] JIANG T, ZUO F, WANG L G. Achievement of auto-focusing in severe defocused state[J]. Laser Technology, 2015, 39(6):794-797(in Chinese). [9] JARVIS R. Focus optimization criteria for computer image processing[J]. Microscope, 1976, 24(2):163-180. [10] CHEN G J, ZHU M F, WANG Y K, et al. Study on definition evaluation function based on image contrast variation[C]//Proceedings of the 2007 China-Ireland International Conference on Information and Communications Technologies. Dublin, Ireland: IET, 2007: 254-258. [11] GAO Z, JIANG W, ZHU K F, et al. Auto-focusing algorithm based on Roberts gradient[J]. Infrared and Laser Engineering, 2006, 35(1):117-121(in Chinese). [12] ZHAI Y P, ZHOU D X, LIU Y H, et al. Design of evaluation index for auto-focusing function and optimal function selection[J]. Acta Optica Sinica, 2011, 31(4):0418002(in Chinese). doi: 10.3788/AOS [13] PENG G J. Video information transmission and processing and application technology development of remote microscopy workstation[D].Guilin: Guilin University of Electronic Technology, 2015: 34-35(in Chinese). [14] ZHU Q, JIANG W, BEN X Y, et al. Auto-focusing algorithm based on gradient and correlation[J]. Optical Technique, 2016, 42(4):329-332(in Chinese). [15] MARICHAL X, MA W Y, ZHANG H J. Blur determination in the compressed domain using DCT information[J]. IEEE Xplore, 2002, 2(2):386-390. [16] XIAN Zh Y, GAN J M, YU Zh M, et al. A method for detecting image defocus blurred region based on correlation and local standard deviation[J]. Computer Applications and Software, 2014, 31(9):198-200(in Chinese). [17] ZHAI Y P, LIU Y H, ZHOU D X, et al. Autofocusing method for microscopy with low image content density[J]. Journal of Software, 2012, 34(5):1281-1294(in Chinese). [18] LI H G, WANG Sh, SHA X P, et al. Study of auto focusing technique of micro-vision system[J]. Opto-Electronic Engineering, 2014, 41(8):1-9(in Chinese). -
点击查看大图
计量
- 文章访问数: 4904
- HTML全文浏览量: 3134
- PDF下载量: 249
- 被引次数: 0
