网站地图
-
激光打孔是以激光为热源的热加工过程，加热表面材料并向材料内部进行热传导，使得材料熔化，形成熔融层。随着温度增加达到材料沸点，材料开始汽化，材料蒸发会产生饱和蒸汽压克服表面张力去除液态金属[1-4]。激光打孔过程中材料去除包含蒸发和液体排出，液体排出消耗能量远远小于蒸发。因此，在打孔过程中需要重点考虑反冲力作用下的液体排出速度[5-6]。实际应用中，激光打孔的潜在效率得不到充分利用，主要由于熔融物阻碍了激光向材料内部渗透，排出熔融物需要消耗大量激光能量，导致激光打孔效率降低[7-8]。
为了解决上述问题，人们提出复合激光打孔的方法。FOX[9]于1975年提出一种改善连续激光对金属的穿透力的方法，连续激光叠加一束脉冲激光作用于不锈钢板，可以有效地利用连续激光的能量，同时脉冲起到去除熔融物的作用，结果不仅缩短了打孔时间并且减少了重铸层。1979年, ROBIN [10]和TOWLE，McKAY[11]等人建立连续激光和脉冲激光结合打孔的理论模型，描述材料去除过程以及对脉冲激光的最低要求。2001年, LEHANE和KWOK[12]使用两束Nd: YAG激光作用于303不锈钢来提高打孔效率，最终得出长脉宽的高能量脉冲和短脉宽的低能量脉冲结合效果最佳。WANG和MICHALOWSKI[13]等人于2009年提出一种对不锈钢板打孔的方法，将单束激光分束为两束纳秒脉冲激光，进行单束激光打孔和叠加激光打孔的对比实验，结果表明, 叠加打孔可有效改善打孔效率，短脉冲激光具有打孔的潜能。
目前实验以及理论研究都表明复合激光打孔可以提高打孔效率[14]。但采用何种参量的激光进行叠加，存在最佳匹配问题。本文中在理论和实验上研究了复合激光打孔的最佳匹配参量。理论上，长脉冲激光能量用于熔化金属材料并形成熔池；短脉冲激光峰值功率用于去除熔融物。当熔融物的产生和去除达到平衡时，根据理论模型得到复合激光打孔的最佳匹配参量，以及复合打孔的最佳打孔速率。实验中，利用毫秒脉冲和纳秒脉冲Nd: YAG激光器叠加作用于不锈钢材料进行激光打孔实验，分析实验结果得到最佳匹配参量。理论模型和实验结果均表明，当长脉冲激光和短脉冲激光在最佳匹配的情况下打孔，复合激光打孔速率达到最大，激光能量得到充分利用。
-
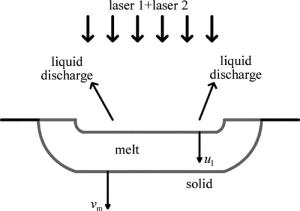
复合激光打孔的示意图如图 1所示。长脉冲激光标记为laser 1，短脉冲激光标记为laser 2。复合激光打孔中，长脉冲激光能量主要用于形成熔融层，并向材料内部延伸，熔化速率设为vm，短脉冲激光的主要作用是形成饱和蒸气压，产生反作用力使得金属材料以液体形式排出，液体排出的速率为ul。复合激光打孔中，蒸发去除金属材料所占比例极小，在模型中不考虑金属蒸汽的影响。理论上，当vm和ul相等时，熔融物的产生和去除达到平衡，长脉冲激光和短脉冲激光的参量达到最佳匹配。
Figure 1. Schematic diagram of drilling by the combined laser
von ALLMEN在1976年对金属材料的激光打孔速率进行研究，在忽略表面张力、热传导损失和蒸发吸收的情况下，提出包含液体排出速率和蒸发速率的激光打孔模型[15]。考虑表面张力的影响改善激光打孔模型，可得到激光打孔速率公式[15-16]如下所示：
$ {j_{\rm{v}}} = (1 - \alpha ){p_{\rm{s}}}{\left( {\frac{m}{{2{\rm{ \mathsf{ π} }}k{T_0}}}} \right)^{1/2}} $
(1) $ {j_{\rm{l}}} = {\left[ {\left( {\frac{{2a}}{r}} \right){\rm{ln}}\left( {\frac{{{T_0}}}{{{T_{\rm{r}}}}}} \right)} \right]^{1/2}}{p_{\rm{s}}}^{1/4}{\rho ^{3/4}} $
(2) $ u = \frac{{{j_{\rm{v}}} + {j_{\rm{l}}}}}{\rho } = {u_{\rm{v}}} + {u_{\rm{l}}} $
(3) 式中，jv和jl分别是蒸发比率和液体去除比率；T0为表面温度; u为打孔速率, 由蒸发速率uv和液体排出速率ul组成；α是材料表面反射系数；ρ为金属材料密度；k为玻尔兹曼常数；m为粒子质量；ps为饱和压力；r为光斑半径；a为热扩散率[15]; Tr为液体去除阈值温度，即达到阈值温度才可以克服表面张力使得液体排出。对于不锈钢材料，表面张力大小约为200×105N，阈值温度在3380K左右[17]。
长脉冲激光的熔化速率vm的计算公式[11]如下所示：
$ {v_{\rm{m}}} = \frac{{{\alpha _1}I}}{{\rho c\Delta {T_{\rm{m}}} + \rho {L_{\rm{m}}}}} $
(4) 式中，α1为金属材料吸收系数，I为功率密度，c为比热容，ΔTm为熔点温度和环境温度差值，Lm为熔化潜热。
-
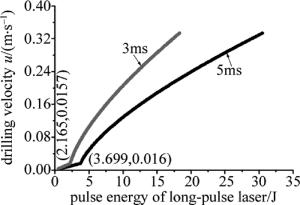
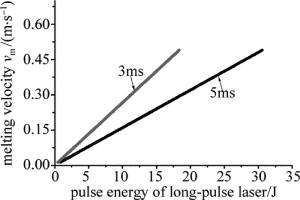
选择不锈钢作为激光打孔材料，不锈钢材料的物理性质如表 1所示。M表示摩尔质量，Tm和Tv分别为熔化温度和汽化温度，Lv为汽化潜热。将不锈钢物理性质代入(1)式~(3)式，可以得到长脉冲激光单独打孔的速率与激光功率密度之间的关系，由于长脉冲激光的功率密度受激光脉冲能量和脉宽的影响, 因此，可以得到不同脉宽的长脉冲激光的脉冲能量和打孔速率u之间的关系，如图 2所示。根据(4)式可得到不同脉宽的长脉冲激光脉冲能量与熔化速率vm之间的关系，如图 3所示。
physical properties stainless steel M 55.8g/mol ρ 7800kg/m3 Tm 1811K Tv 3135K c 418J/(kg·K) Lm 2.72×105J/kg Lv 6.33×106J/kg κ 41.84W/(m·K) a 4.9×10-6m2/s 
Figure 2. Relationship between drilling velocity and pulse energy of long-pulse laser
Figure 3. Relationship between the melting velocity and pulse energy of long-pulse laser
根据图 2可得，长脉冲激光单独打孔速度随脉冲能量增长的过程有个转折点，在转折点处打孔速率迅速提高。这个转折点表明不锈钢材料温度达到液体去除的阈值温度(3380K)。在转折点之前，材料去除的方式只有蒸发；在转折点之后，材料去除方式是蒸发和液体溅射。根据脉宽3ms和5ms时的情况对比可知，在相同脉冲能量情况下，脉宽较小的激光打孔速率更大，因为脉宽较小的长脉冲激光峰值功率较大，导致液体去除速率会更快，因此打孔速率更大。
在复合激光打孔中，长脉冲激光的主要作用是熔化不锈钢材料，形成熔融物。在长短脉冲参量达到最佳匹配的情况下，复合激光打孔最大速率由长激光熔化不锈钢材料的速率决定，根据图 2和图 3的对比可知，复合激光打孔的最佳打孔速率是长脉冲激光单独打孔速率的1.24倍~3.68倍。
-
1992年，BASU和DEBROY提出激光对金属材料作用过程中的液体排出模型，用于计算液体排出方式占金属材料去除的比例，根据这个模型可得到短脉冲激光作用下不锈钢材料表面温度的变化情况，如以下公式[17]所示：
$ \begin{array}{l} {T_0} = {T_{\left( {n - 1} \right)/f}} + 2I\sqrt {\frac{{t - \left( {n - 1} \right)/f}}{{{\rm{ \mathsf{ π} }}\kappa \rho c}}} , \\ \left( {\frac{{n - 1}}{f} \le t \le \frac{{n - 1}}{f} + {t_{\rm{p}}}} \right) \end{array} $
(5) $ \begin{array}{l} {T_0} = {T_{\left( {n - 1} \right)/f}} + 2I\left[ {\sqrt {\frac{{t - \left( {n - 1} \right)/f}}{{{\rm{ \mathsf{ π} }}\kappa \rho c}}} - } \right.\\ \left. {\sqrt {\frac{{t - {t_{\rm{p}}} - \left( {n - 1} \right)/f}}{{{\rm{ \mathsf{ π} }}\kappa \rho c}}} } \right], \\ \left( {\frac{{n - 1}}{f} + {t_{\rm{p}}} \le t \le \frac{n}{f}} \right) \end{array} $
(6) 式中, n表示脉冲数；T(n-1)/f表示第(n-1)个脉冲作用后的表面温度；t为激光照射时间；tp为脉宽；f为频率；κ为材料的热导率[17]。初始温度选为不锈钢材料的熔点温度(1811K)。
根据(5)式~(6)式可知，表面温度受短脉冲激光的参量影响。选择峰值功率密度为1×107W/cm2、脉宽为20ns、频率为10kHz的短脉冲激光。作用于初始温度为1811K的不锈钢熔融物，表面温度随激光照射时间变化曲线如图 4a所示。将表面温度代入(2)式可得液体排出速率随时间变化的曲线，如图 4b所示。
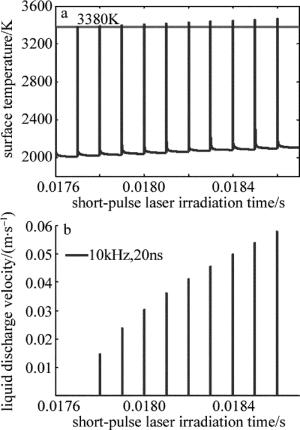
Figure 4. Relationship between surface temperature, liquid discharge velocity and irradiation time of short-pulse laser
根据图 4a可知，短脉冲激光作用下，熔融物表面温度随着照射时间逐渐增加。每个脉冲作用下，表面温度先是迅速上升至最高温度，再降低至最低温度。相对于前一个脉冲表面温度都有所增加。当熔融物的最高温度超过3380K，才开始会有液体排出。
根据图 4b可知，在短脉冲激光作用的前期还没有液体排出速率，主要是因为熔融物的表面温度未达到液体排出的阈值温度。达到阈值温度后，每个脉冲的作用下，液体排出速度会迅速上升至最大值，但持续时间很短。相对于前一个脉冲液体排出速度有所增加。
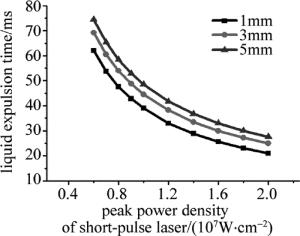
对每个脉冲的液体排出速度进行时间积分即可得到排出不同厚度的不锈钢熔融物所需时间。脉宽为20ns、频率为10kHz的短脉冲激光作用于不锈钢熔融物，对其液体排出速度积分，进行计算得到不同峰值功率密度下排出1mm，3mm，5mm不锈钢熔融物所需时间，如图 5所示。
图 5 Relationship between liquid discharge time and peak power density of short-pulse laser
根据图 5可得，液体排出时间随着短脉冲激光的峰值功率增加是逐渐减小的；对不同厚度的熔融物，相同峰值功率密度的短脉冲作用下，液体排出时间与厚度并不成正比。例如，对于峰值功率1×107W/cm2，排出1mm, 3mm, 5mm熔融物所需时间分别为39ms，44.5ms，48.5ms。这主要是因为相同参量的短脉冲激光作用于不同厚度的熔融物，达到阈值温度的时间相同，达到阈值温度之后液体排出速率会随着激光照射时间逐渐增加。因此熔融物厚度越大，短脉冲激光发挥的作用越大。
-
通过第2.1节和第2.2节中的理论分析可以得到：长脉冲激光和短脉冲激光作用于相同厚度不锈钢材料所需的熔化时间和液体排出时间。理论上，当熔化时间和液体排出时间相等时，长脉冲激光和短脉冲激光达到最佳匹配情况。材料熔化速率受到长脉冲激光的脉冲能量和脉宽影响，熔融物排出速率由短脉冲的峰值功率密度决定。因此，复合激光打孔中，最佳匹配参量指的是长脉冲激光的脉冲能量和短脉冲激光的峰值功率密度。最佳匹配情况下，两者的关系曲线如图 6所示。
Figure 6. Optimal matching parameters for long-pulse laser and short-pulse laser with different pulse widths
根据图 6可知，对于1mm厚的不锈钢板，对于相同脉宽的长脉冲激光，随着脉冲能量增加，所需匹配的峰值功率密度增加；相同脉冲能量下，3ms脉宽的长脉冲激光熔化速率大于5ms脉宽的长脉冲激光，因此所需匹配的短脉冲激光的峰值功率密度较大。在最佳匹配情况下，复合激光的打孔速率即为长脉冲激光的熔化速率。根据最佳匹配参量的增长趋势可知，峰值功率密度随着脉冲能量增加的速度越来越大，然而当峰值功率密度超过1×107W/cm2，会产生等离子屏蔽效应[12]，影响激光的吸收。因此，当匹配的峰值功率密度较大时，复合打孔的效率会受到等离子体的影响。
-
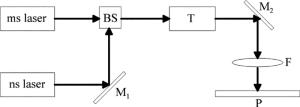
实验装置图如图 7所示。包括两台Nd: YAG固体激光器(激光器参量如表 2所示)，布儒斯特镜(BS)，扩束准直系统(T)，两片反射镜(M1, M2)，聚焦透镜(F)和5mm厚不锈钢板(P)。两束激光通过布儒斯特镜后合束，复合激光束经过扩束准直系统，通过焦距为150mm的聚焦透镜，聚焦于厚度为5mm的不锈钢板表面。
Figure 7. Experimental setup of drilling by the combined laser
Table 2. The parameters of the ms pulsed laser and the ns pulsed laser
pulse width frequency pulse energy radius ms laser 3ms~5ms 30Hz 2J~5J 0.5mm ns laser 20ns 10kHz 0.9mJ~1.92mJ 0.5mm -
实验中采用不同脉宽和脉冲能量的长脉冲激光与不同峰值功率密度的短脉冲激光复合作用于不锈钢板，记录不锈钢板打穿时间，得到复合激光打孔时间与短脉冲峰值功率密度、长脉冲激光能量和脉宽的关系曲线，实验结果如图 8所示。
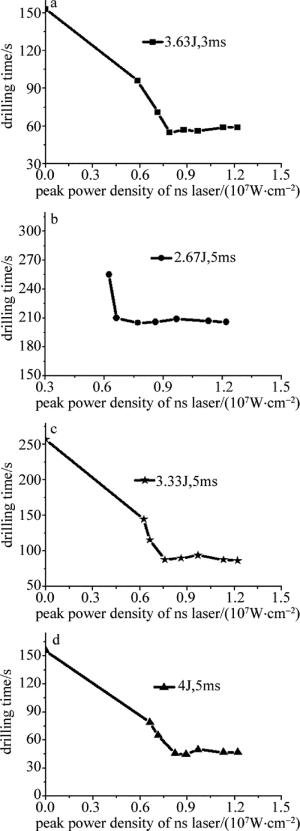
Figure 8. Relationship between drilling time and peak power density with di-fferent parameters of the combined laser
根据图 8的实验结果可知，复合激光打孔中匹配的纳秒脉冲激光存在最佳峰值功率密度。在达到最佳峰值功率密度之前，随着纳秒脉冲激光峰值功率密度增加，复合激光打孔时间逐渐减小；打孔时间最低点即为最佳匹配点，之后打孔时间基本不变，是因为匹配的纳秒脉冲激光峰值功率密度过大，毫秒脉冲激光熔化速度不够，没有熔融物排出。
在4种不同参量的毫秒脉冲激光器单独打孔中，图 8a单独打孔时间最短为153s。最佳复合打孔时间为57s，打孔速率提高倍数为2.68倍，所需匹配的最佳峰值功率密度为7.89×106W/cm2。根据图 8b、图 8c、图 8d对比可知，对于相同脉宽的毫秒脉冲激光，随着脉冲能量增加，单独打孔时间降低，所需匹配的最佳峰值功率密度会增加，达到的最佳复合打孔时间降低。图 8d中单独打孔时间为155.7s，所需匹配的最佳峰值功率密度为8.22×106W/cm2，最佳复合打孔时间是47s，打孔速率提高倍数为3.3倍。
-
实验结果表明:长脉冲激光和短脉冲激光复合打孔可以有效提高打孔速率，并且两束激光存在最佳匹配参量，达到最佳匹配参量时，复合打孔速率达到最大。实验结果证明了理论模型的正确性和整体趋势，但具体匹配的数值两者存在差异。究其原因，主要是因为：(1)实验过程中一些因素，如合束过程中光束同轴性和镜片污染等带来的激光能量损失、钢板穿孔的判断标准、穿孔过程中重铸层的影响等，使得实验数据出现误差；(2)理论模型进行了简化，材料对激光的吸收率是随温度以及材料形态变化，为了方便计算，理论上选取固定值；忽略复合激光打孔中的蒸发速度；两束激光对熔化材料和去除材料均有贡献，但理论上只考虑各自发挥的主要作用。
-
本文中对长脉冲激光和短脉冲激光复合打孔参量的最佳匹配进行了理论分析和实验研究。理论模型中，长脉冲激光能量主要用于熔化不锈钢形成熔融层，短脉冲激光作用于熔融物产生饱和蒸汽压克服表面张力排出熔融物。以熔融物的产生和去除达到平衡为匹配准则，即长脉冲激光的熔化速率等于短脉冲激光的液体排出速率，理论计算得到长脉冲激光和短脉冲激光复合打孔中的最佳匹配参量。采用毫秒脉冲激光和纳秒脉冲激光复合激光束作用于5mm不锈钢板进行打孔实验，结果表明, 复合激光打孔能提高激光打孔效率，纳秒脉冲激光对某一参量的长脉冲激光存在最佳峰值功率密度。在最佳匹配的情况下，复合激光打孔速率相比于毫秒脉冲激光单独打孔最大提高了3.3倍。
理论模型和实验结果均证明了复合激光打孔中存在最佳匹配参量，当达到最佳匹配时，复合激光打孔速率达到最大，激光能量得到充分利用。研究结果为复合激光打孔中的激光参量选择提供理论参考，更大程度地提高了激光打孔的效率。
复合激光打孔最佳匹配参量的研究
Study on the optimum matching parameters of the combined laser drilling
-
摘要: 为了有效提高激光打孔的速率和激光能量的利用率，采用长脉冲激光和短脉冲激光空间叠加打孔的方法，对复合激光打孔的最佳匹配参量进行了理论和实验研究。建立复合激光打孔最佳匹配模型，以熔融物的产生和去除达到平衡为准则，理论计算得出长脉冲激光和短脉冲激光的最佳匹配参量和最佳匹配情况下的复合激光打孔速率。同时进行了毫秒脉冲和纳秒脉冲的Nd：YAG激光器复合作用于5mm的不锈钢板的打孔实验。结果表明，在实验中得到的最佳匹配参量下，复合激光打孔速率相比于毫秒脉冲激光单独打孔最大提高了3.3倍。实验和理论模型均证明了复合激光打孔在最佳匹配状态下，打孔速率达到最大，激光能量得到充分利用。Abstract: In order to improve laser drilling velocity and the utilization of laser energy, the optimal matching parameters of the combined laser drilling were studied by means of space superposition drilling by long-pulse laser and short-pulse laser. The optimal matching model of the combined laser drilling was established. Based on the balance of generation and expulsion of the melted metal, the optimal parameters of long-pulse laser and short-pulse laser, and the combined laser drilling velocity at the optimum matching point were obtained theoretically. The combined laser drilling of stainless steel with the thickness of 5mm was performed with ms and ns pulse Nd:YAG lasers. The experimental results show that in the case of the optimum matching, the combined laser drilling velocity is 3.3 times higher than that of the ms pulse laser alone. Both theory and experiments indicate that the maximum drilling velocity can be obtained at the optimum matching point, and laser energy is fully utilized.
-
Key words:
- laser technique /
- laser drilling /
- the combined laser /
- optimum matching /
- drilling efficiency
-
Figure 3. Relationship between the melting velocity and pulse energy of long-pulse laser
Figure 4. Relationship between surface temperature, liquid discharge velocity and irradiation time of short-pulse laser
a—surface temperature b—liquid discharge velocity
图 5 Relationship between liquid discharge time and peak power density of short-pulse laser
Figure 6. Optimal matching parameters for long-pulse laser and short-pulse laser with different pulse widths
Figure 8. Relationship between drilling time and peak power density with di-fferent parameters of the combined laser
physical properties stainless steel M 55.8g/mol ρ 7800kg/m3 Tm 1811K Tv 3135K c 418J/(kg·K) Lm 2.72×105J/kg Lv 6.33×106J/kg κ 41.84W/(m·K) a 4.9×10-6m2/s 
下载: 导出CSV
Table 2. The parameters of the ms pulsed laser and the ns pulsed laser
pulse width frequency pulse energy radius ms laser 3ms~5ms 30Hz 2J~5J 0.5mm ns laser 20ns 10kHz 0.9mJ~1.92mJ 0.5mm
下载: 导出CSV
-
[1] UGLOV A A, KOKORA A N, OREKHOV N V. Laser drilling of holes in materials with different thermal properties[J]. Soviet Journal of Quantum Electronics, 1976, 6(3):311-315. doi: 10.1070/QE1976v006n03ABEH011007 [2] ARMON E, ZVIRIN Y, LAUFER G, et al. Metal drilling with a CO2 laser beam. Ⅰ. Theory[J]. Journal of Applied Physics, 1989, 65(12):4995-5002. doi: 10.1063/1.343171 [3] OLSON R W, SWOPE W C.Laser drilling with focused Gaussian beams[J]. Journal of Applied Physics, 1992, 72(8):3686-3696. doi: 10.1063/1.352313 [4] DAHOTRE N B, HARIMKAR S. Laser fabrication and machining of materials[M].New York, USA:Springer, 2008:97-100. [5] UGLOV A A, KOKORA A N. Thermophysical and hydrodynamic effects in laser-beam processing of materials (review)[J]. Soviet Journal of Quantum Electronics, 1977, 7(6):671-678. doi: 10.1070/QE1977v007n06ABEH012871 [6] CHAN C L, MAZUMDER J. One-dimensional steady-state model for damage by vaporization and liquid expulsion due to laser-material interaction[J]. Journal of Applied Physics, 1987, 62(11):4579-4586. doi: 10.1063/1.339053 [7] FOX J A, SLUSS E C. The effect of combining cw laser radiation with pulses[C]//AIAA 16th Aerospace Sciences Meeting. Huntsville, USA: Aircraft Industries Association of America, 1978: 16-18. [8] WAGNER R E. Laser drilling mechanics[J]. Journal of Applied Physics, 1974, 45(10):4631-4637. doi: 10.1063/1.1663102 [9] FOX J A. A method for improving continuous wave laser penetration of metal targets[J]. Applied Physics Letters, 1975, 26(12):682-684. doi: 10.1063/1.88024 [10] ROBIN J E, NORDIN P. Improved CW laser penetration of solids using a superimposed pulsed laser[J]. Applied Physics Letters, 1976, 29(1):3-5. doi: 10.1063/1.88864 [11] TOWLE L C, McKAY J A, SCHRIEMPF J T. The penetration of thin metal plates by combined CW and pulsed-laser radiation[J]. Journal of Applied Physics, 1979, 50(6):4391-4393. doi: 10.1063/1.326427 [12] LEHANE C, KWOK H S. Enhanced drilling using a dual-pulse Nd:YAG laser[J]. Applied Physics, 2001, A73(1):45-48. [13] WANG X D, MICHALOWSKI A, WALTER D, et al. Laser drilling of stainless steel with nanosecond double-pulse[J]. Optics & Laser Technology, 2009, 41(2):148-153. [14] HE Y J, WANG W, XU B Zh, et al. The experimental study on deep laser drilling by superposed pulsed lasers[J]. Laser Technology, 2017, 41(3):380-384(in Chinese). [15] von ALLMEN M. Laser drilling velocity in metals[J]. Journal of Applied Physics, 1976, 47(12):5460-5463. doi: 10.1063/1.322578 [16] BATANOV V A, BUNKIN F V, PROKHOROV A M, et al. Evaporation of metallic targets caused by intense optical radiation[J]. Journal of Experimental & Theoretical Physics, 1973, 36(2):311-322. [17] BASU S, DEBROY T. Liquid metal expulsion during laser irradiation[J]. Journal of Applied Physics, 1992, 72(8):3317-3322. doi: 10.1063/1.351452 -
点击查看大图
图(8) / 表(2)
计量
- 文章访问数: 6940
- HTML全文浏览量: 4879
- PDF下载量: 306
- 被引次数: 0
