网站地图
-
一些先进的显微术，包括扫描电子显微镜、扫描隧道显微镜、共聚焦扫描显微镜、荧光显微镜、傅里叶位相显微镜、衍射位相显微镜等[1-3], 由于存在非无损、非实时、测量信息不全面、精度不够高等限制，使得一些活细胞高精度的实时监测难以实现，然而远场光学显微镜可在自然环境下对生物样品实现实时无扫描的快速成像。但是受到光的衍射效应和有限孔径的影响，使得光学显微镜存在分辨率极限[4-5]，难以满足更高精度的要求，因此，进一步提高远场光学显微镜的分辨率一直是人们比较关心和重要的问题。
国内外学者提出了许多能够提高光学分辨率的方法[6-7]，其中利用光瞳滤波器来调制波前实现光斑压缩，是实现光学超分辨的有效手段之一。主要分为振幅型光瞳滤波器和相位型光瞳滤波器，均在不同程度提高了分辨率。其中SHEPPARD等人设计出了幂指数变化的振幅型光瞳滤波器[8]。浙江大学ZHANG团队和河北工程大学WANG团队设计出了环形光瞳滤波器[9-11]。XIAO和YUAN等人设计出了三区复振幅光瞳滤波器[12]和正弦变化的光瞳滤波器[13]。ZHU等人设计出了“非三明治”结构的光瞳滤波器[14]等。
本文中提出了一种振幅透过率随半径呈幂函数分布的光瞳滤波器，并推导出其夫琅禾费衍射的光强度分布函数[15-21]，通过MATLAB软件，画出其衍射图样。根据光学超分辨影响因素，对比衍射分布的主瓣强度、主瓣宽度和旁瓣强度，分析斯特雷尔比S、最大旁瓣强度比M、分辨参量G和分辨率提高倍数，从而研究其对分辨率的影响。
-
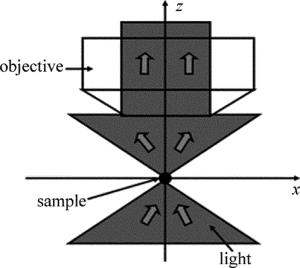
常规远场光学显微系统的全孔径照明方式，是将来自光源的光，经过聚光镜会聚后，一圆锥型光照射在样品上，经过样品又以圆形光锥的方式照射到显微物镜，其过程如图 1所示。
Figure 1. Illumination system in a microscope
激光经过扩束准直后照明样品，样品上物点发出球面波，这个球面波以理想像点为中心，由于出射光瞳的限制作用，在像平面将产生一个以理想像点为中心的夫琅禾费衍射图像。设其像面光场的复振幅分布为Ui(xi, yi)，根据标量衍射理论[15]，观察到的像面光场Ui(xi, yi)可以通过对光瞳上场分布U(x, y)的傅里叶变换求出，其计算公式如下：
$ \begin{array}{l} {U_{\rm{i}}}({x_{\rm{i}}}, {y_{\rm{i}}}) = \frac{{{\rm{exp}}({\rm{j}}kz){\rm{exp}}\left[ {{\rm{j}}\frac{k}{{2z}}({x_{\rm{i}}}^2 + {y_{\rm{i}}}^2)} \right]}}{{{\rm{j}}\lambda z}} \times \\ \int_{ - \infty }^\infty {} \int_{ - \infty }^\infty {} U\left( {x, y} \right){\rm{exp}}\left[ {{\rm{ - j}}\frac{{2{\rm{ \mathsf{ π} }}}}{{\lambda z}}({x_{\rm{i}}}x + {y_{\rm{i}}}y)} \right]{\rm{d}}x{\rm{d}}y \end{array} $
(1) 式中，z为光瞳面到像面的衍射距离，λ为光波长，k为波数，且k=2π/λ。
从给定点光源在物平面(xo, yo)发出球面波，经过光瞳面(x, y)。给定观察面(xi, yi)上的坐标示意图，如图 2所示, 其中(xo, yo), (x, y), (xi, yi)平面相互平行。
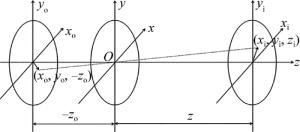
Figure 2. Coordinate diagram of a divergent point light source passing through an aperture to the observation plane
设光瞳用一个无限远处的点光源产生的单位振幅、垂直入射的平面波照射，则光瞳上的场分布就等于光瞳函数P(x, y)，即U(x, y)=P(x, y)。光瞳函数P(x, y)在光瞳内其值为P(x, y)，在光瞳外其值为0，积分遍及整个光瞳面。于是(1)式积分化为：
$ \begin{array}{l} {U_{\rm{i}}}({x_{\rm{i}}}, {y_{\rm{i}}}) = \frac{{{\rm{exp}}({\rm{j}}kz){\rm{exp}}\left[ {{\rm{j}}\frac{k}{{2z}}({x_{\rm{i}}}^2 + {y_{\rm{i}}}^2)} \right]}}{{{\rm{j}}\lambda z}} \times \\ \int_{ - \infty }^\infty {} \int_{ - \infty }^\infty {} P(x, y){\rm{exp}}\left[ {{\rm{ - j}}\frac{{2{\rm{ \mathsf{ π} }}}}{{\lambda z}}({x_{\rm{i}}}x + {y_{\rm{i}}}y)} \right]{\rm{d}}x{\rm{d}}y \end{array} $
(2) 可以看出, 这个式子除了积分号前相乘的相位因子外，就是孔径函数的傅里叶变换，在频率fx=xi/(λz)和fy=yi/(λz)上求值，即：
$ \begin{array}{l} {U_{\rm{i}}}({x_{\rm{i}}}, {y_{\rm{i}}}) = \frac{{{\rm{exp}}({\rm{j}}kz){\rm{exp}}\left[ {{\rm{j}}\frac{k}{{2z}}({x_{\rm{i}}}^2 + {y_{\rm{i}}}^2)} \right]}}{{{\rm{j}}\lambda z}} \times \\ \int_{ - \infty }^\infty {} \int_{ - \infty }^\infty {} P(x, y){\rm{exp}}[ - {\rm{j}}2{\rm{ \mathsf{ π} }}({f_x}x + {f_y}y)]{\rm{d}}x{\rm{d}}y \end{array} $
(3) 将上式利用傅里叶-贝塞尔变换[15]，则：
$ \begin{array}{l} {U_{\rm{i}}}\left( {{r_{\rm{i}}}} \right) = \frac{{{\rm{exp}}({\rm{j}}kz)}}{{{\rm{j}}\lambda z}}{\rm{exp}}\left( {{\rm{j}}\frac{k}{{2z}}{r_{\rm{i}}}^2} \right)2{\rm{ \mathsf{ π} }} \times \\ \int_0^\infty {} {{\rm{J}}_{\rm{0}}}(2{\rm{ \mathsf{ π} }}\rho r)P\left( r \right)r{\rm{d}}r \end{array} $
(4) 式中，$ {r_{\rm{i}}} = \sqrt {{x_{\rm{i}}}^2 + {y_{\rm{i}}}^2} $，ρ为频域半径，$ \rho = \frac{{{r_{\rm{i}}}}}{{\lambda z}}$；J0()是0阶贝塞尔函数。
这是一个含有r的0阶贝塞尔函数乘以一个关于r的光瞳函数再乘以r的积分式。作者设计出不同的光瞳滤波器，就会有不同的光瞳函数P(r)，从而计算出不同的像面复光场，然后通过光强公式求出像面光强分布，此即为光学系统的点扩散函数，根据衍射主瓣宽度，就可确定其是否能够提高分辨率。
本文中研究振幅透过率随半径呈幂函数分布的振幅型光瞳滤波器，其光瞳函数为：
$ {P_{n, w}}\left( r \right) = {\rm{circ}}(r{w^{ - 1}}){\left( {r{w^{ - 1}}} \right)^n} $
(5) 式中，w为光瞳半径，n为幂次。n=0时，即光瞳函数为P0, w(r)=circ(rw－1)(rw－1)0，称为全孔径；n=1时，即光瞳函数为P1, w(r)=circ(rw－1)(rw－1)1，称为1次透光孔；……；n=n时，即光瞳函数为Pn, w(r)=circ(rw－1)(rw－1)n，称为n次透光孔。
当光瞳滤波器半径归一化时设为rn, n从0~3时的振幅透过率函数t(无量纲)，如图 3所示。
Figure 3. Function of transmittance and radius
将光瞳函数Pn, w(r)=circ(rw－1)(rw－1)n带入(4)式得到：
$ \begin{array}{l} {U_{\rm{i}}}\left( {{r_{\rm{i}}}} \right) = \frac{{{\rm{exp}}({\rm{j}}kz)}}{{{\rm{j}}\lambda z}}{\rm{exp}}\left( {{\rm{j}}\frac{k}{{2z}}{r_{\rm{i}}}^2} \right)2{\rm{ \mathsf{ π} }} \times \\ \int_0^w {} {{\rm{J}}_{\rm{0}}}(2{\rm{ \mathsf{ π} }}\rho r){\rm{circr}}\left( {\frac{r}{w}} \right){\left( {\frac{r}{w}} \right)^n}r{\rm{d}}r \end{array} $
(6) 则衍射光强分布为：
$ I({r_{\rm{i}}}) = |{U_{\rm{i}}}({r_{\rm{i}}}){|^2} $
(7) -
在上述理论推导的基础上，利用MATLAB软件编程，模拟衍射分布图样。实验照明光波长为450nm，孔径光阑半径为0.05m，紧挨光阑的透镜焦距为1m(即衍射距离为1m)，像面观察屏半径为10μm。
-
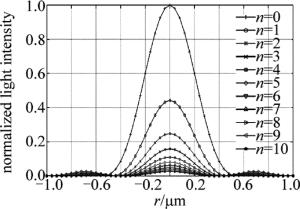
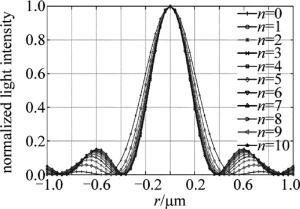
现画出光瞳函数为Pn, 0.05(r)=circ(0.05－1r)×(0.05－1r)n时，n从0~10的衍射分布即点扩散函数。由图 4可以看到，n越大，衍射主瓣峰值强度越小；由图 5可以看到，n越大，衍射旁瓣峰值强度越大；衍射主瓣直径越窄。n的次数继续增加，衍射图像变化微小，分析意义不大，因此只比较前面变化较为明显n从0~3的4项，得出其变化规律即可。
Figure 4. Light intensity normalized to full aperture when n=0~10
Figure 5. Light intensity normalized to itself when n=0~10
-
利用MATLAB软件，模拟当光瞳函数为Pn, 0.05(r)=circ(0.05－1r)(0.05－1r)n，n为0, 1, 2, 3这4种情况下的衍射分布，对比衍射主瓣宽度(衍射分布曲线中两个第一极小值点之间的距离即为主瓣宽度)、主瓣光强、旁瓣强度，从而确定分辨率的变化规律。
图 6为n从0~3时光瞳滤波器的形式，从圆心到边缘振幅透过率呈幂函数分布。其中, n=0时为全孔径，在光瞳滤波器w内振幅透过率无衰减全部通过；n为1, 2, 3时，在光瞳滤波器w内振幅透过率随着半径增大从0逐渐增大到1。
Figure 6. Optical pupil filters when n=0~3
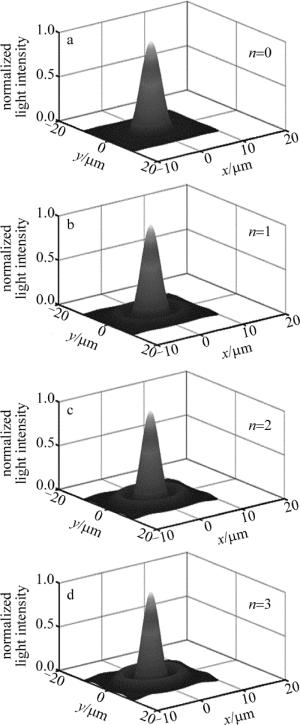
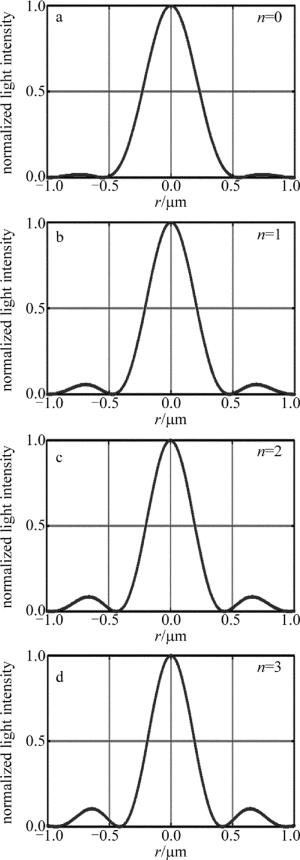
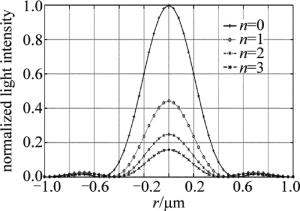
图 7、图 8、图 9均为衍射分布。其中图 7为n从0~3时的2维衍射光斑; 图 8为n从0~3时的归一化衍射3维光强图; 图 9为n从0~3时归一化衍射光强曲线图。可以看到不同幂次的透光孔，其衍射光斑有差异。n从0依次增大到3时，衍射分布中：主瓣宽度逐渐减小；主瓣光强逐渐减小；旁瓣光强逐渐增大。
Figure 7. 2-D distribution of diffraction intensity when n=0~3
Figure 8. 3-D distribution of diffraction intensity when n=0~3
Figure 9. Normalized light intensity when n=0~3
-
斯特雷尔比S描述光斑相对于艾里斑的亮度，是指中心焦点处超分辨模型情况下和艾里斑模型情况下的光强度比。将n从0~3时衍射曲线对全孔径时归一化，如图 10所示。
Figure 10. Light intensity normalized to full aperture when n=0~3
由图 10可知，全孔径照明理想成像归一化时所对应的主瓣峰值强度为1；1次透光孔所对应的中心主瓣峰值强度为0.4445；2次透光孔所对应的中心主瓣峰值强度为0.2450；3次透光孔所对应的中心主瓣峰值强度为0.1600。由此可以看到，幂次越高的透光孔，因为其光瞳中心处的透过率小，导致通过光瞳的透光量减少，因此衍射分布主瓣光强度越低，不利于超分辨观察。
-
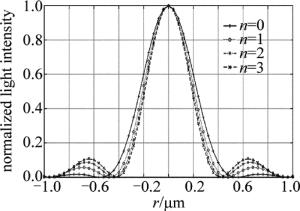
最大旁瓣强度比M表示在全孔径及超分辨情况下旁瓣的峰值强度和中心主瓣峰值强度的比值。为了方便对比，现将n从0~3时衍射曲线对自身归一化，如图 11所示。
Figure 11. Light intensity normalized to itself when n=0~3
由图 11可知，全孔径照明理想成像条件下所对应旁瓣的峰值强度为0.0175；1次透光孔所对应旁瓣的峰值强度为0.0570；2次透光孔所对应旁瓣的峰值强度为0.0857；3次透光孔所对应旁瓣的峰值强度为0.1053。从图中可以看到，随着幂次的增加，旁瓣强度在逐渐增加，因此噪声也在增加，可以采取图像滤波的方式减小旁瓣的影响。
-
分辨参量G用来衡量超分辨的程度，是指焦平面上超分辨光斑两个第一极小值之间的距离与艾里斑的第一极小值之间的距离之比，即主瓣宽度之比。将图 11右半部分第一极小值点放大，如图 12所示。
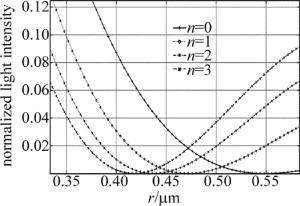
Figure 12. The enlarged image of the right part of Fig. 11 for the first minimum values
由图 12可知，全孔径照明理想成像条件下所对应的主瓣宽度约为2×0.55μm；1次透光孔所对应的主瓣宽度约为2×0.47μm；2次透光孔所对应的主瓣宽度约为2×0.44μm；3次透光孔所对应的主瓣宽度约为2×0.42μm。可以看到，不同幂次的透光孔，衍射主斑宽度不同，并且光瞳函数幂次越高，衍射主瓣宽度越小。由显微系统分辨率的定义可知，分辨率的高低直接依赖于衍射光斑的主瓣尺寸，主瓣尺寸越小，分辨率越高。因此可知光瞳函数幂次越高，其光学显微镜分辨能力越强。
为了方便对比，列出数据见表 1。表格中的参量有斯特雷尔比S、最大旁瓣强度比M、分辨参量G、分辨率提高倍数[9-10]。应知道S值越大，M值越小，G值越小，分辨率提高倍数rn=0/rn=1, 2, 3(即全孔径时的主瓣宽度与超分辨情况下的主瓣宽度之比)越大，分辨率越高。
Table 1. Parameters of pupil filters when n=0~3
n=0 n=1 n=2 n=3 transfer function P0, 0.05(r) P1, 0.05(r) P2, 0.05(r) P3, 0.05(r) the main lobe width 2×0.55μm 2×0.47μm 2×0.44μm 2×0.42μm S 1 0.4445 0.2450 0.1600 M 0.0175 0.0570 0.0857 0.1053 G 1 0.8545 0.8000 0.7636 rn=0/rn=1, 2, 3 1 1.1702 1.2500 1.3095 根据图 10、图 11、图 12以及表 1可以看到，随着光瞳函数Pn, w(r)=circ(rw－1)(rw－1)n中n次数的增加，其衍射分布的主瓣宽度明显减小。优点是分辨参量在减小，因此衍射主瓣宽度在减小；比全孔径提高的倍数也在增加，这些对于提高分辨率都是有利的。然而伴随的缺点是斯特雷耳比在减小，说明主瓣强度减小，不利于观察；最大强度旁瓣比在增加，说明干扰噪声也在增加。因此如何既能提高分辨率，又有利于观察，就需要对于振幅透过率随半径呈幂函数分布的光瞳滤波器选择一个最优幂次。
-
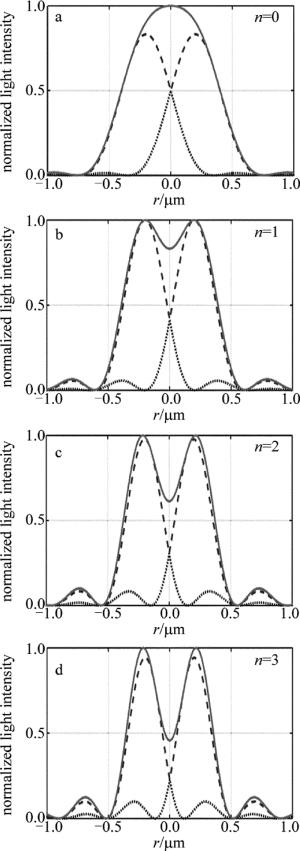
为了更加直观地表示出随着光瞳函数Pn, w(r)=circ(rw－1)(rw－1)n中n次数的增加，系统是如何提高分辨率，可对比n从0~3时，两个相隔400nm的点像光强和其合光强的曲线图，结果如图 13所示。
Figure 13. Intensity curves of two points and their combined intensity when n=0~3
由图 13可以看到，随着幂级次的增加，衍射主瓣宽度依次减小，两者的合光强中心光强逐渐降低，从而两个点像逐渐分开，进而达到超分辨的效果。文中只考虑了两个点光源，而实际中的总强度有可能是多个点光源的叠加，但是依据分辨率判断标准，仍不失为评价一个成像系统的分辨率质量依据。
-
本文中提出了振幅透过率随半径呈幂函数分布的光瞳滤波器，光瞳函数为Pn, w(r)=circ(rw－1)×(rw－1)n，通过理论推导和MATLAB仿真模拟，给出n从0~3时光通过光瞳滤波器的衍射强度分布、3维图像、截面曲线以及两个点像的光强曲线。通过对比斯特雷尔比、最大旁瓣强度比、分辨参量和分辨率提高倍数，得到随着振幅透过率幂次数的增加，主瓣宽度依次减小、主瓣光强度依次降低和旁瓣光强度依次增大。从而可知，增加振幅透过率随半径成幂函数分布的光瞳滤波器的幂次数可以提高分辨率，改善显微镜成像质量，如当幂次数为3时，模拟仿真的成像分辨率比全孔径时提高1.3倍；但伴随的缺点是观察到像光强度的减小和旁瓣影响的增加。期望这一研究可为远场光学显微镜实现超分辨成像提供一种新的技术路径。
幂函数分布的振幅型光瞳滤波器
Amplitude optical pupil filters with power function distribution
-
摘要: 为了提高衍射远场显微成像的分辨率，采用一种振幅透过率随半径呈幂函数分布的光瞳滤波器进行了理论分析和数值模拟。通过在光路中加入幂函数分布的振幅型光瞳滤波器，利用标量衍射理论推导出夫琅禾费衍射分布的计算公式；通过MATLAB软件给出衍射图样，对比衍射分布的主瓣宽度。结果表明，当幂次数为3时，模拟仿真的衍射分布斯特雷尔比为0.16，最大旁瓣强度比为0.1，分辨参量为0.76，分辨率提高倍数为1.3；随着振幅透过率幂次数的增加，主瓣宽度依次减小；同时也伴随着主瓣强度降低和旁瓣强度增大的缺点。这一研究对于远场光学显微镜实现超分辨成像是有帮助的。Abstract: In order to improve the resolution of far-field diffraction microscopy, a pupil filter whose amplitude transmittance had the distribution of power function with radius was proposed. Theoretical analysis and numerical simulation were carried out. By using scalar diffraction theory, the formula of Fraunhofer diffraction distribution was derived when an amplitude pupil filter with the distribution of power function was added in optical path. Diffraction pattern was obtained through MATLAB software, and the main lobe width of diffraction distribution was compared. The results show that when the power number is 3, Strehl ratio of diffraction distribution is 0.16, the maximum sidelobe intensity ratio is 0.1, the resolution parameter is 0.76, and the enhancement factor of resolution is 1.3. With the increase of power number of amplitude transmittance, the main lobe width decreases. At the same time, the main lobe intensity decreases and the side lobe intensity increases. This study is helpful for the realization of super-resolution imaging in the far field optical microscopes.
-
Figure 2. Coordinate diagram of a divergent point light source passing through an aperture to the observation plane
Figure 12. The enlarged image of the right part of Fig. 11 for the first minimum values
Table 1. Parameters of pupil filters when n=0~3
n=0 n=1 n=2 n=3 transfer function P0, 0.05(r) P1, 0.05(r) P2, 0.05(r) P3, 0.05(r) the main lobe width 2×0.55μm 2×0.47μm 2×0.44μm 2×0.42μm S 1 0.4445 0.2450 0.1600 M 0.0175 0.0570 0.0857 0.1053 G 1 0.8545 0.8000 0.7636 rn=0/rn=1, 2, 3 1 1.1702 1.2500 1.3095 
下载: 导出CSV
-
[1] LIU Y, CHEN J B.A method of analyzing the axial intensity in a confocal fiber system[J]. Laser Technology, 2006, 30(5):558-560(in Chinese). [2] PARK Y K, POPESCU G, BADIZADEGAN K, et al. Diffraction phase and fluorescence microscopy[J]. Optics Express, 2006, 14(18):8263-8268. doi: 10.1364/OE.14.008263 [3] POPESCU G, DEFLORES L P, VAUGHAN J C. Fourier phase microscopy for investigation of biological structures and dynamics[J]. Optics Letters, 2004, 29(21):2503-2505. doi: 10.1364/OL.29.002503 [4] RAYLEIGH L. On the manufacture and theory of diffraction gratings[J]. Philosophical Magazine, 1874, 47(310):81-93. [5] AO Q J. Optical course[M]. Beijing:Higher Education Press, 1990:424(in Chinese). [6] WANG T Y, XU Zh P, ZHU H F, et al. Effect of incident light field distribution on superresolution and DOF of superresolution pupil filter[J]. Laser & Optoelectronics Progress, 2014, 51(11):112301(in Chinese). [7] WANG W. Superresolution technology of gaussian beam under high numerical aperture[J]. Acta Photonica Sinica, 2013, 42(4):441-446(in Chinese). doi: 10.3788/gzxb [8] SHEPPARD C J R, HEGEDUS Z S. Axial behavior of pupil plane filters[J]. Journal of the Optical Society of America, 1988, A5(2):643-647. [9] ZHI Sh T, ZHANG H J, ZHANG D X. Super-resolution optical microscopic imaging method based on annular illumination with high numerical aperture[J]. Acta Physica Sinica, 2012, 61(2):024207(in Chinese). [10] ZHI Sh T. Super-resolution optical microscopic imaging method and system based on annular aperture[D]. Hangzhou: Zhejiang University, 2012: 15-28(in Chinese). [11] LIU F F. Investigation of exact phase reconstruction algorithm and expeiments in digital holographic microscopy[D]. Handan: Hebei University of Engineering, 2013: 30-34(in Chinese). [12] XIAO F R, YUAN J H, WANG G Y, et al. Design of 3-zone amplitude-type superresolution pupil filters[J]. Acta Optica Sinica, 2004, 24(1):1-4(in Chinese). [13] XIAO F R, YUAN J H, WANG G Y, et al. Amplitude optical pupil filters with sine functions[J]. Acta Optica Sinica, 2005, 25(5):647-650(in Chinese). [14] ZHU H F, LIU W S, HENG K Y, et al. Non-sandwich-structured tunable transverse superresolving pupil filters bases on birefringent crystals[J]. Chinese Journal of Lasers, 2012, 39(10):1016002(in Chinese). doi: 10.3788/CJL [15] JOSEPH W. Goodman, introduction to fourier optics[M]. 3rd ed. Beijing:Publishing House of Electronics Industry, 2011, 5:46-65(in Chinese). [16] LI J Ch, XIONG B H. Information optics course[M]. Beijing:Science Press, 2011:17-54(in Chinese). [17] QIAN X F. Information optics theory and calculated[M]. Beijing:Science Press, 2015:22-55(in Chinese). [18] YU D Y, TAN H Y. Engineering optics[M]. Beijing:China Machine Press, 2011:206-208(in Chinese). [19] CHANG S, WU B, SANG Z W, et al. Analysis and processing of field curvature without astigmatism based on diffraction theory[J]. Journal of Applied Optics, 2011, 32(2):245-249(in Chinese). [20] CHANG Sh, WU B, SANG Zh W, et al. Calculation of the diffraction field of a circular aperture irradiated by a point source[J]. Jiangxi Science, 2009, 27(6):816-819(in Chinese). [21] CHANG Sh, WU B, SANG Zh W, et al. Two calculation methods for three kinds of circular aperture diffraction[J]. Journal of Applied Optics, 2010, 31(5):734-740(in Chinese). -
点击查看大图
图(13) / 表(1)
计量
- 文章访问数: 5148
- HTML全文浏览量: 3174
- PDF下载量: 186
- 被引次数: 0
