-
当今随着数字光纤通信的快速发展,局域网和用户环路迅速扩展的需求不断上升,半导体光电器件逐步朝着光集成、光电集成的方向发展。当波长为1.31μm和1.55μm附近时,光纤损耗的色散最小,所以近年来,国内研制的大多数半导体激光器的波长都在1.31μm和1.55μm波段。
由于InGaAsP/InP材料的激光器起步较早,因此成为在1.31μm波段内研究最成熟的材料。波长在1.31μm和1.55μm波段的激光器是当前光纤通信技术的基础。在制备InGaAsP/InP材料的激光器,一般选用与衬底材料晶格相匹配的四元材料组分,这样可以优化器件的性能。在综合对比了两种不同材料的特性后,作者选用AlGaInAs/InP作为生长量子阱的材料,因为AlGaInAs/InP材料的导带带阶ΔEc=0.72ΔEg(ΔEg为禁带宽度),而InGaAsP/InP材料的ΔEc=0.4ΔEg[1]。由于InGaAsP/InP材料导带偏移比较小,势阱不能很好地限制电子,容易发生载流子的泄露,从而减少激光器在发光过程中受激辐射的概率,进而影响到所制备激光器的多项基本的性能参量[2]。AlGaInAs/InP材料的垒和阱之间的带阶比较大,这样就能有效地限制载流子在势阱中,减少载流子向外的泄露,从而提高量子效率,改善元件的高线性、大功率特性。
国外的一些研究机构先后都进行了AlGaInAs/InP材料的激光器的相关理论和实验生长研究[3-4]。国内在该种材料激光器研制方面的研究报道相对比较少,目前作者正在研制AlGaInAs/InP材料的激光器。目前较为普遍的研究做法是在该种四元材料体系中采用有比较大的压应变量的AlGaInAs材料作为有源区势阱层,势垒层采用与InP衬底晶格相匹配的AlGaInAs材料,但由于势阱的应变量较大,材料在生长过程中容易由2维生长向3维生长转变,造成生长缺陷,导致量子阱的生长界面粗糙,影响了器件的发光效率。因此,作者在研究过程中在AlGaInAs势垒层引入适当的张应变进行应变补偿,这样可以根据应变补偿原理,避免在生长过程中的一些生长缺陷,从而保证了量子阱的发光效率。同时有研究表明,在势垒中引入适当的张应变可以增大能带的带阶,从而提高了载流子的限制能力,与在设计结构上没有引入应变补偿的激光器相比,设计结构上引入应变补偿的激光器具有更大的增益和更小的阈值电流。
-
对于应变补偿多量子阱结构,QUILLEC等人提出的应变补偿的思想,势垒层材料和势阱层材料的应变类型相反时,通过调节势垒层材料应变量的大小和垒层厚度,使得最终结构净应变为零[5]。这种结构就可以在实现有源区应变多量子阱结构外延生长时,不用去考虑有源区由于应变的累积效应而存在的临界厚度问题。进而避免了超出临界厚度之后,整个量子阱激光器的生长质量下降,导致发光效率降低的问题。
对于AlGaInAs/InP压应变量子阱来说,在势垒层引入适当的张应变量,可以根据应变补偿的思想,从而减小整个有源区的应变量。理论上应变补偿结构可以克服有源区的临界厚度对大应变、多周期的量子阱结构的限制。而实际设计过程中不会达到完全的应变补偿,但可以采用适当的张应变量的势垒层,使得平均应变量趋近于零。
垒层的禁带宽度Eg, b只有在大于阱层的禁带宽度Eg, w时,这样才能限制载流子。由于所设计的激光器的激射波长为1.31μm,该波长所对应的跃迁能级差为0.947eV, 为了限制载流子在阱层,所以垒层的禁带宽度必须大于0.947eV, 同时为了实现应变补偿,保证有源区的整体结构的良好生长,所以势垒层决定采用具有0.4%张应变的Al0.263Ga0.267In0.47As。
-
对于三元和四元半导体化合物的相关性能参量,例如晶格常数、应变系数和有效质量等参量,可以利用组成其化合物的二元半导体材料的参量,采用线性插值的方法求出[6]。所以对于AxByC1-x-yD型的四元系化合物半导体材料,可以看作是由3个二元化合物AB, AC和AD组成,计算AlxGayIn1-x-yAs四元化合物材料相应的性能参量分别为:
$ \begin{array}{l} P({\rm{A}}{{\rm{l}}_x}{\rm{G}}{{\rm{a}}_y}{\rm{I}}{{\rm{n}}_{1 - x - y}}{\rm{As}}) = xP\left( {{\rm{AlAs}}} \right) + \\ yP\left( {{\rm{GaAs}}} \right) + (1 + x + y)P\left( {{\rm{InAs}}} \right) \end{array} $
(1) 式中, P代表化合物的性能参量,例如晶格常数、应变系数等;x和y分别为Al和Ga元素在AlxGayIn1-x-yAs四元化合物中所占的组分;二元系材料AlAs, GaAs和InAs的参量参照表 1所列。
Table 1. Parameters used in the calculation[6]
parameter symbol/unit AlAs GaAs InAs for conduction band ac/eV -5.64 -7.17 -5.08 for valence band av/eV 2.47 1.16 1.00 shear deformation potential b/eV -1.5 -1.7 -1.8 lattice constant a/nm 0.566 0.565 0.606 elastic stiffness C11/(1011dyn·cm-2) 12.5 11.879 8.329 constant C12/(1011dyn·cm-2) 5.34 5.376 4.526 electron effective mass me* 0.15 0.067 0.026 heavy-hole effective mass mh, h* 0.76 0.51 0.41 light-hole effective mass ml, h* 0.15 0.087 0.026 Luttinger-Kohn band γ1 3.45 6.8 20.4 structure parameter γ2 0.68 1.9 8.3 conduction band position EcH/eV 2.5255 1.53 0.801 valence band position EvH/eV -0.4245 0.111 0.441 因为在半导体化合物中同族原子呈随机性分布,所以会导致化合物的晶体势没有周期性,因而很难精确地计算出半导体材料的能带结构。大量的实验与研究表明,很大一部分Ⅲ-Ⅴ族化合物材料的禁带宽度与其化合物的各组分之间不是线性变化的关系[7]。根据参考文献[8], 可以近似计算得到AlxGayIn1-x-yAs在室温下的禁带宽度:
$ \begin{array}{l} {E_{{\rm{g, o}}}}\left( {x, y} \right) = 0.36 + 0.629y + 2.093x + 0.436{y^2} + \\ \;\;\;\;\;\;\;0.577{x^2} + 1.013xy - 2xy(1 - x - y) \end{array} $
(2) 式中,Eg, o是无应变量子阱禁带宽度。由于在有源区设计的是具有1.12%压应变量子阱,所以在计算禁带宽度时,还需将应变对禁带宽度的影响考虑进去。由于压应变使能带结构中的导带上移,价带下移,所以阱层的压应变带宽Eg比无应变时的Eg, o宽[9]。
两种带隙不等的半导体材料交替向上生长从而形成有源区,如图 1所示。图中, aw和ab分别代表势阱层和势垒层的晶格常数,Vc表示导带,Vh, h和Vl, h分别代表重、轻空穴带,Eg, w和Eg, b分别代表势阱层和势垒层的禁带宽度,ΔVc表示导带带阶,δs和δh分别代表切向应力和水静压。在两种半导体材料外延生长时,由于每层生长的材料组分不同,进而晶格常数是不同的,当上层的晶格常数大于下层的晶格常数时,外延层就会横向压缩,产生压应变,使晶格常数与衬底匹配。同时能带结构中导带会向上漂移,而价带则向下漂移,这时的禁带宽度就会比没有应变时的禁带宽度宽许多,如图 1a所示。反之,发生张应变。在其能级结构中导带和价带的漂移方向与压应变相反,故而禁带宽度会比没有应变时的禁带宽度窄, 如图 1c所示。
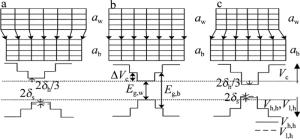
Figure 1. Strain condition and band change in different crystal lattices a—compressive strain b—no strain c—tensile strain
其次,应变会使能带结构发生变形。增大价带的曲率半径(即减小空穴有效质量)[1],扭转无应变情况下导带与价带严重不平衡的局面,使准费米能级近似的对称分布,在带间产生准费米能级差时,载流子密度可以相对无应变能带结构时所需密度有所减小。在有源区中采用应变量子阱后,由于四元半导体材料的带隙和能带状态密度都发生了改变,因此可以拓展现有的激光器的波长,同时激光器的性能如输出功率得到提高,阈值电流得到降低。
基于应变理论[10-11],在(001)方向生长时,应变量定义为[12]:
$ \varepsilon = \left( {{a_0} - a} \right)/{a_0} $
(3) 式中,ε表示应变量,a0为量子阱材料的晶格常数,a为势垒材料的晶格常数。
量子阱层的导带边漂移值为:
$ {\rm{ \mathit{ δ} }}{E_{\rm{c}}}(x, y) = 2{a_{\rm{c}}}(1 - {C_{12}}/{C_{11}})\varepsilon $
(4) 式中,C11和C12为弹性应变系数,ac为导带的静压力形变势,δEc为压应变导致的导带能带移动。
量子阱层的价带漂移值为:
$ {\rm{ \mathit{ δ} }}{E_{{\rm{h, h}}}}\left( {x, y} \right) = 2{a_{\rm{v}}}(1 - {C_{12}}/{C_{11}}) + b(1 - 2{C_{12}}/{C_{11}})\varepsilon $
(5) 式中, av为价带的静压力形变势,b为切变形变势,δEh, h为由应变导致的重空穴带的能带移动。
因此,量子阱的压应变带宽为:
$ {E_{\rm{g}}}\left( {x, y} \right) = {E_{{\rm{g, o}}}}(x, y) + {\rm{ \mathit{ δ} }}{E_{\rm{c}}}(x, y) - {\rm{ \mathit{ δ} }}{E_{{\rm{h, h}}}}(x, y) $
(6) 势阱和势垒材料的带边差就是带阶,采用Harrison模型[11]计算了价带位置和导带位置分别为:
$ {E_{\rm{v}}}(x, y) = {E_{\rm{v}}}^{\rm{H}}(x, y) + {\rm{ \mathit{ δ} }}{E_{{\rm{h, h}}}}(x, y) $
(7) $ {E_{\rm{v}}}(x, y) = {E_{\rm{v}}}^{\rm{H}}(x, y) + {\rm{ \mathit{ δ} }}{E_{{\rm{l, h}}}}(x, y) $
(8) $ {E_{\rm{c}}}\left( {x, y} \right) = {E_{\rm{c}}}^{\rm{H}}(x, y) + {\rm{ \mathit{ δ} }}{E_{\rm{c}}}(x, y) $
(9) 式中, Ev(x, y)和, Ec(x, y)表示四元化合物的价带位置和导带位置,EvH(x, y)为二元化合物价带位置,EcH(x, y)为二元化合物导带位置,可以从表 1中得到,上标H表示厄米共轭。δEh, h(x, y)和δEl, h(x, y)是价带重空穴和轻空穴的漂移值。
利用(7)式~(9)式可以分别求出势阱层和势垒层的, Ev(x, y)和, Ec(x, y),进而应变量子阱结构的价带带阶ΔEv和导带带阶ΔEc可以分别求出。在压应变量子阱结构中,因为导带和价带各自的能带偏移比较小,所以量子阱对电子和空穴的限制能力比较弱,势垒层引入适当大小的张应变补偿后,可以增大有源区势阱和势垒之间的能带带阶,进而使量子阱对载流子有更好的限制能力,使激光器具有较大的增益。
依据克龙尼克-潘纳模型[13],可以求解出阱结构中量子化子能级。电子从导带第一子带向价带第一子空穴带的跃迁决定了量子阱激光器的激射波长[14]。应变量子阱中,由于应变的存在,所以轻、重空穴退简并,对于压应变量子阱来说,重空穴带是价带子能级的带顶,对张应变量子阱,轻空穴带是价带子能带的带顶。
导带第一子能带的能量值为:
$ {E_{{\rm{c,1}}}} = \left[ {{{\hbar}^{\rm{2}}}/(2m_{\rm{c}}^*)} \right]{({\rm{ \mathit{ π} }}/d)^2} $
(10) 重空穴带第一子能带的能量值为:
$ {E_{{\rm{h,h,1}}}} = \left[ {{{\hbar}^{\rm{2}}}/(2m_{\rm{h}}^{\rm{*}})} \right]{({\rm{ \mathit{ π} }}/d)^2} $
(11) 式中,$\hbar$为约化普朗克参量,mc*和mh*分别为势阱中电子和空穴的有效质量,d为势阱的宽度,Ec, 1为导带第一子能带的能量值,Eh, h, 1为价带第一子能带的能量值。
由于势阱层是压应变,受到应变的影响, 重空穴的有效质量减少,电子的有效质量不发生变化,mh*表示为:
$ {m_{\rm{h}}}^{\rm{*}} = 1/({\gamma _1} - 2{\gamma _2}) $
(12) 式中,γ1和γ2为拉廷格-科恩能带结构参量。
压应变量子阱激光器的激射波长为:
$ \lambda = hc/({E_{\rm{g}}} + {E_{{\rm{c, 1}}}} + {E_{{\rm{h, h, 1}}}}) $
(13) 式中, h为普朗克常数,c为真空中光速,λ为激射波长。
通过求解上式可以确定在量子阱不同组分处的激射波长,因此在设计激光器时,可以根据需要的激射波长确定量子阱材料的组分。
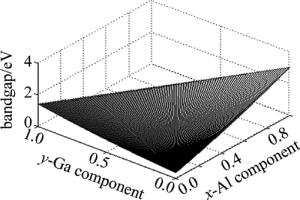
图 2为使用MATLAB计算出的AlxGayIn1-x-yAs材料的应变带隙随AlxGayIn1-x-yAs材料组分(即x, y)的变化图。由于所设计的激光器的激射波长为1.31μm,在量子阱中,发生跃迁的光子的能量必须要大于阱的禁带宽度[15],(13)式表明量子阱的激射波长与跃迁光子能量成反比,在计算量子阱的禁带宽度时,要选择禁带宽度小于辐射波长1.31μm的跃迁光子能量,所以材料的应变带隙要小于0.947eV。经过理论分析,阱层取x=0.156,y=0.152,计算得到的结果如表 2所示, 表中ae和as表示阱层和垒层的晶格常数。由计算结果中可以看出Eg, w和Eg, b符合理论要求。
Table 2. Calculation results of each parameter
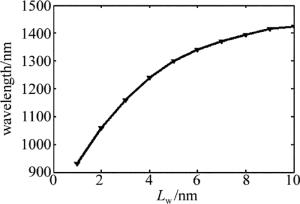
parameter result ac -5.485eV av 1.254eV b -1.738eV Eg, w 0.884eV ae 0.594nm C11 9.519×1011dyn·cm-2 C12 4.782×1011dyn·cm-2 Eg, b 1.121eV as 0.585nm δEc 0.082eV δEh, h 0.034eV 综合导带和价带的带阶,以及量子化子能级,计算出激射波长随阱宽的变化。图 3是Al0.156Ga0.152In0.692As组分波长随阱宽Lw变化曲线图。由图中可以看出,在阱宽为5nm时,波长在1310nm附近。最终得到阱宽为5nm的Al0.156Ga0.152In0.692As结构符合要求。
激光器势阱层就采用5nm厚、具有1.12%压应变的Al0.156Ga0.152In0.692As,为了实现有源区的应变补偿,选用具有0.4%张应变的Al0.263Ga0.267In0.47As的势垒层, 其激射波长满足所需要的1.31μm。
-
由于半导体激光器的体积小,工作机理较为复杂,生长工艺难度高,所以在实际制备激光器之前,利用ALDS软件进行仿真建模。ALDS是一种半导体激光器常用的功能较为强大的计算机仿真软件,可以提供仿真建模的半导体激光二极管方案。在ALDS软件中,可以设计激光器的材料组分、阱宽垒宽和操作条件等。然后可以通过软件的阈值分析,稳态分析等模块得出所设计激光器的各项性能参量。
作者所研制的1.31μm波长的AlGaInAs/InP应变补偿的多量子阱激光器的脊宽为2.5μm的脊形波导结构的法布里-珀罗激光器芯片,解理为300μm的腔长。有源区由7组1.12%的压应变、5nm厚的AlGaInAs阱层和0.4%的张应变、9nm厚的AlGaInAs垒层构成。波导层为渐变折射率分别限制波导结构。生长的应变补偿多量子阱具体结构参量如表 3所示。
Table 3. Structure parameters of AlGaInAs/InP laser
number material thickness/ nm concentration/ cm-3 1 Ga0.47In0.53As 150 1×1019 2 InP 150 3 In0.85Ga0.33AsP 20 5×1017 4 InP
AlxGa0.47-xIn0.53As(x:0.36~0.44)170
1005×1017 5 7×Al0.156Ga0.152In0.692As
7×Al0, 253Ga0.267In0.47As5
9no
no6 AlxGa0.47-xIn0.53As(x:0.44~0.36) 100 5×1017 7 Al0.48In0.52As 140 8×1017 8 N-InP 500 1×1018 9 N-InP 2×1018 使用ALDS软件对所设计的量子阱激光器进行了仿真建模,经阈值分析该激光器在室温25℃下具有Ith=9mA的低阈值电流,稳态分析后得到斜率效率为η=0.4W/A。这些结果为目前文献中报道的优秀水平。同时利用仿真软件,在温度设置为25℃时,0mA~ 100mA的偏置电流下,设计了一个在势垒层没有引入张应变补偿的激光器来进行对比,得出了仿真结果。
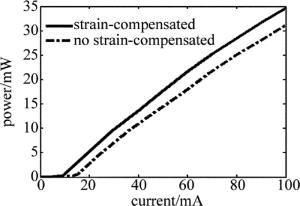
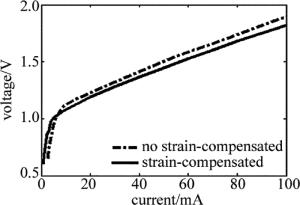
该组对比激光器的功率-电流(P-I)曲线见图 4。电压-电流(U-I)曲线见图 5。P-I曲线和U-I曲线都可以清晰地看出:应变补偿量子阱结构相较于未进行应变补偿的量子阱结构可以明显地改善激光器的功率和电压。作者所设计的具有应变补偿结构的多量子阱激光器与未进行应变补偿设计的多量子阱激光器相比,阈值电流更低,斜率效率更高。
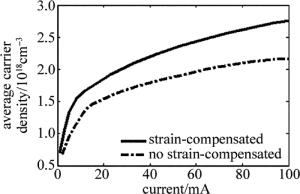
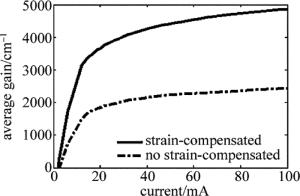
该组对比激光器的平均载流子密度曲线见图 6。平均增益曲线见图 7。平均载流子密度曲线和平均增益曲线都清晰地反映出相较于未进行应变补偿的多量子阱结构,应变补偿多量子阱结构对激光器的载流子密度和平均增益有明显的提高。
-
经过理论计算有源区四元材料的相关参量,确定势阱层和势垒层的各项参量,使用ALDS软件进行了仿真建模,得出了对于腔长300μm的器件,在室温25℃下具有Ith=9mA的低阈值电流,斜率效率η=0.4W/A,反映出该器件有良好的性能参量。同时设计了对比试验,对比了在势垒层引入适当的张应变补偿和没有引入补偿即与衬底晶格适配的势垒层,分析对比了P-I曲线、U-I曲线、载流子密度电流曲线、平均增益电流曲线,为设计1.31μm AlGaInAs/InP材料的量子阱激光器提供了一个新的尝试思路。
AlGaInAs/InP应变补偿多量子阱激光器
AlGaInAs/InP strain-compensated multiple quantum well laser
-
摘要: 为了优化在长距离光纤通讯系统中采用的1.31μm波长的量子阱激光器,对AlGaInAs/InP材料的有源区应变补偿的量子阱激光器进行了设计研究。采用应变补偿的方法,根据克龙尼克-潘纳模型理论计算出量子阱的能带结构,设计出有源区由1.12%的压应变AlGaInAs阱层和0.4%的张应变AlGaInAs垒层构成。使用ALDS软件对所设计出的器件进行了建模仿真,对其进行了阈值分析和稳态分析。结果表明,在室温25℃下,该激光器具有9mA的低阈值电流和0.4W/A较高的单面斜率效率;在势垒层采用与势阱层应变相反的适当应变,可以降低生长过程中的平均应变量,保证有源区良好的生长,改善量子阱结构的能带结构,提高对载流子的限制能力,降低阈值电流,提高饱和功率,改善器件的性能。
-
关键词:
- 激光器 /
- 量子阱结构 /
- 应变补偿 /
- AlGaInAs/InP
Abstract: In order to optimize the quantum well laser at 1.31μm wavelength in long distance optical fiber communication systems, strain compensated quantum well in active region of AlGaInAs/InP material was studied. Based on strain compensation method and Kronig-Panna model theory, the band structure of quantum well was calculated. The active region was consisted of 1.12% compressive strain AlGaInAs well layer and 0.4% tensile strain AlGaInAs barrier layer. ALDS software was used to simulate the design of the device and analyze the threshold and the steady state. The results show that the laser has a low threshold current of 9mA and a high slope efficiency of 0.4W/A at 25℃room temperature. In the potential barrier layer, the appropriate strain opposite to the strain of the potential well layer can reduce the average strain in the growth process, ensure the well growth of active zone, improve the band structure of quantum well effectively, enhance the limit ability of carriers, reduce threshold current, increase saturation power and improve device performance.-
Key words:
- lasers /
- quantum well structure /
- strain compensation /
- AlGaInAs/InP
-
Table 1. Parameters used in the calculation[6]
parameter symbol/unit AlAs GaAs InAs for conduction band ac/eV -5.64 -7.17 -5.08 for valence band av/eV 2.47 1.16 1.00 shear deformation potential b/eV -1.5 -1.7 -1.8 lattice constant a/nm 0.566 0.565 0.606 elastic stiffness C11/(1011dyn·cm-2) 12.5 11.879 8.329 constant C12/(1011dyn·cm-2) 5.34 5.376 4.526 electron effective mass me* 0.15 0.067 0.026 heavy-hole effective mass mh, h* 0.76 0.51 0.41 light-hole effective mass ml, h* 0.15 0.087 0.026 Luttinger-Kohn band γ1 3.45 6.8 20.4 structure parameter γ2 0.68 1.9 8.3 conduction band position EcH/eV 2.5255 1.53 0.801 valence band position EvH/eV -0.4245 0.111 0.441 Table 2. Calculation results of each parameter
parameter result ac -5.485eV av 1.254eV b -1.738eV Eg, w 0.884eV ae 0.594nm C11 9.519×1011dyn·cm-2 C12 4.782×1011dyn·cm-2 Eg, b 1.121eV as 0.585nm δEc 0.082eV δEh, h 0.034eV Table 3. Structure parameters of AlGaInAs/InP laser
number material thickness/ nm concentration/ cm-3 1 Ga0.47In0.53As 150 1×1019 2 InP 150 3 In0.85Ga0.33AsP 20 5×1017 4 InP
AlxGa0.47-xIn0.53As(x:0.36~0.44)170
1005×1017 5 7×Al0.156Ga0.152In0.692As
7×Al0, 253Ga0.267In0.47As5
9no
no6 AlxGa0.47-xIn0.53As(x:0.44~0.36) 100 5×1017 7 Al0.48In0.52As 140 8×1017 8 N-InP 500 1×1018 9 N-InP 2×1018 -
[1] CHEN T H, CHE X H, ZHANG Y, et al. Study of materials for 1.3μm AlGaInAs/InP quantum well lasers[J]. Micronanoeletronic Technology, 2013, 50(4):220-223(in Chinese). [2] MA H, YI J X, JIN J Y, et al. Design and fabrication of 1.3μm uncooled AlGaInAs/InP strain-compensated quantum well lasers[J]. Acta Photonica Sinica, 2002, 31(2):191-195(in Chinese). [3] SELMIC S R, CHOU T M, SIH J P, et al. Design and characterization of 1.3μm AlGaInAs-InP multiple-quantum-well lasers[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2001, 7(2):340-349. doi: 10.1109/2944.954148 [4] TAKEMASA K, KUBOTA M, MUNAKATA T, et al. 1.3μm AlGaInAs buried-heterostructure lasers[J]. IEEE Photonics Technology Letters, 1999, 11(8):949-951. doi: 10.1109/68.775309 [5] QUILLEC M, DAGUET C, BENCHIMOL J L, et al. Inx Ga1-x Asy P 1-y alloy stabilization by the InP substrate inside an unstable region in liquid phase epitaxy[J]. Applied Physics Letters, 1982, 40(4):325-326. doi: 10.1063/1.93078 [6] XU H W. Structural design and epitaxial growth of 852nm laser diode[D].Changchun: Chinese Academy of Sciences, 2012: 25-26(in Chinese). [7] CHEN F Ch, SHI Y L. Design and fabrication of a 1064nm strain double quantum well laser[J]. Electronic World, 2014(15):157-157(in Chinese). [8] MEI T. Interpolation of quaternary Ⅲ-Ⅴ alloy parameters with surface bowing estimations[J]. Journal of Applied Physics, 2007, 101(1):013520. doi: 10.1063/1.2404791 [9] JIN Zh J. InP based InGaAlAs/InGaAsSb strained quantum well laser materials and design[D].Changchun: Changchun University of Science and Technology, 2008: 30-39(in Chinese). [10] ISHIKAWA T, BOWERS J E. Band lineup and in-plane effective mass of InGaAsP or InGaAlAs on InP strained-layer quantum well[J]. IEEE Journal of Quantum Electronics, 1994, 30(2):562-570. doi: 10.1109/3.283804 [11] YEKTA V B, KAATUZIAN H, YEKTA V B, et al. Simulation and temperature characteristics improvement of 1.3μm AlGaInAs multiple quantum well laser[J]. International Journal of Optics & Applications, 2014, 4(2):46-53. [12] JIANG J P. Semiconductor laser[M]. Beijing:Publishing House of Electronics Industry, 2000:211-220(in Chinese). [13] YAN Ch L, QIN L, NING Y Q, et al. Calculation of energy band structure of GaInAs/GaAs quantum well[J]. Laser Journal, 2004, 25(5):29-31(in Chinese). [14] GUO J, XIE Sh, MAO L H, et al. oprimization of quantum well structure for GaAs/AlGaAs ring lasers[J]. Laser Technology, 2015, 39(5):654-657(in Chinese). [15] HUA L L, YANG Y. Analysis and computation of band offset of strained quantum wells[J]. Laser & Optoelectronics Progress, 2013, 50(5):051404(in Chinese). -


 网站地图
网站地图

 下载:
下载: