网站地图
-
目前轴快流CO2激光器的最高输出水平可以达到45kW，由德国Trumpf激光公司和Fraunhofer激光技术研究所合作开发；工业中所使用的最高功率CO2激光器是德国Trumpf公司推出的20kW激光器；南京东方激光有限公司是我国唯一一家中外合资、引进国外CO2激光器制造技术、开关电源激励技术，生产工业CO2激光器及其应用设备的专业厂商；国内第1台自主研发4kW紧凑型轴快流CO2激光器由华中科技大学激光加工国家工程研究中心、武汉市光谷科威晶激光技术有限公司和武汉华工激光工程有限责任公司共同完成[1-2]。功率开关器件是激励源的核心元件，功率开关器件工作时所产生的热量及时有效地被热沉带走，是保证功率开关器件正常工作的重要条件。作者旨在对轴快流CO2激光器激励源核心功率开关器件冷却用微通道热沉优化设计，发现最优化的结构参量。
TUCKERMAN等人[3]最早进行了微通道冷却技术的研究。TUCKERMAN研制了一个热流密度可达7.9MW/m2的微通道热沉，并通过实验的方法得到热沉接触面和流道入口之间的温差不大于71K。QU等人[4]采用实验以及数值模拟的方法对纵截面为梯形的直通硅基微通道内的传热性能进行了分析。ZHOU等人[5]对三角形直通型硅基微通道热沉采用去离子水作为工质对其的流动和传热特性进行了研究, 分析结果显示，就流动及传热特性而言，微通道与常规尺寸通道有着显著的不同，并且微通道的表面粗糙程度对热沉的散热特征也有着重要的影响。HEE[6]通过实验测试的方法分析了水力直径为106μm~307μm的矩形贯通硅基微通道，在雷诺数为69~800范围内变化时层流流动的压降和传热特性，研究发现, 其所采用的实验参量能很好地匹配常规尺度下工质流体的压降公式，但是常规尺度的换热公式并不适用于微尺度，他们通过实验结果提出了适用于微通道内流体传热的新公式。KANDLIKAR[7]等人分析了微通道结构的散热特征，结果表明, 加快微通道内流体的速度，减小流道的有效长度可以显著地提升热沉的换热效率。LI[8], HEINZ[9]和GIUDICE[10]等人分析了微通道内工质的物性参量在温度发生波动时对微通道热沉换热效率的影响，研究表明, 轴向热量扩散、粘性耗散以及温度变化均会对流体粘度系数产生影响，从而影响微通道内流体的流动和传热特性。VANAKI等人[11]对近十几年来微通道领域公开发表的论文进行了研究，综述了微通道内流体的流动和传热特性，具体分析了流体滑移、表面粗糙度、温度变化等对微通道内流体3维导热、粘性耗散、进口层流发展效应、流体物性等的影响。
对于矩形凹槽结构微通道热沉的优化设计鲜有报道，本文中以CO2激光器射频源功率开关器件冷却用热沉为研究对象，采用计算流体动力学的方法对矩形凹槽的间距P、倾角θ、交错距离s进行了优化设计并得出了最佳尺寸，优化后的结果完全能够满足功率金属-氧化物半导体场效应晶体管(metal-oxide-semiconductor field-effect transistor, MOSFET)正常工作的需要。
-
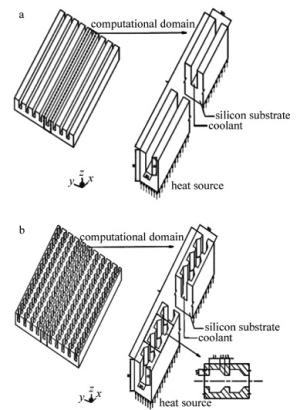
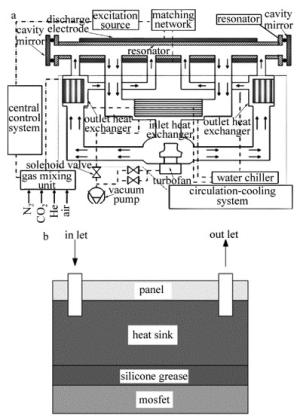
轴快流CO2激光器的结构如图 1a所示，热沉的装配方式如图 1b所示。激励源用于激励放电管中的气体稳定放电，激励源工作时的热稳定性是保证激光器光束质量的关键性因素。
选择功率MOSFET(DRF1201)作为激光器激励源的核心功率器件，通过MOSFET的数据手册查出器件的耗散功率，在后续进行热沉数值模拟时，将耗散功率作为功率热源加载到优化结构后的热沉上，如果经过优化后的热沉上表面的最高温度能够小于技术手册对节温的要求，则证明热沉能够保证MOSFET安全、稳定、长期的工作。结合MOSFET数据手册给出的耗散功率并考虑到40%的裕量，这里取电源功率为1600W，热沉的总面积为16cm2，则热流密度为106W/m2。为了提高计算的效率且不影响计算的结果，本文中截取整个散热器的一部分作为数值模拟的计算域[12]。
Figure 1. a—structural schematic of a fast axial flow CO2 laser b—structure of a heat sink assembly
-
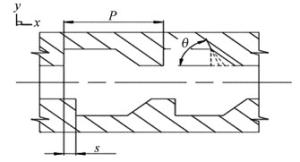
本文中所研究的矩形凹槽结构微通道热沉(rectangular groove micro channel heat sink, RGMCHS)的物理模型是对传统的矩形凹槽结构微通道进行了优化。不带凹槽结构微通道热沉(micro channel heat sink, MCHS)的流道几何结构如图 2a所示，用于与带有凹槽的流道进行比对。带有改进凹槽流道的几何结构如图 2b所示。本文中的模拟分别改变的参量是凹槽角度θ，凹槽间距P以及凹槽交错距离s，具体改变的参量见图 3。在不同入口流速情况下，分别独立改变这些参量的值，用以研究其对微通道热沉的传热性能及流体流动特性的影响。凹槽参量的变化范围见表 1。每个计算模型都是由理想热源、通道和流体工质三部分构成。流体沿x轴正向流动，y轴正向垂直于x轴正向，同时规定x轴、y轴、z轴分别为流向、法向和展向方向。需要说明的是, 图 2b除了凹槽处的结构，其它的结构尺寸与图 2a中所标注的尺寸一致。具体的结构尺寸值见表 2。其中H为热沉高度，L为流道长度，D为流道高度，Wc为流道宽度，Ws为计算域宽度，W1为凹槽深度，L1为优化矩形凹槽短边长度，L2为优化矩形凹槽短边、长边之差，L3为凹槽的间距。
Figure 2. Schematic diagram and detailed view of the computational domain
Figure 3. Detailed view of the channel wall with its design variables
Table 1. Variables of the wall channel
the fixed value variables P=0.2mm, s=0mm θ=90°, 75°, 60°, 45° θ=45°，s=0mm P=0.2mm, 0.4mm, 0.6mm, 0.8mm θ=45°，P=0.2mm s=0mm, 0.05mm, 0.1mm -
本文中进行的数值模拟所选择的计算域见图 2。对整个计算域边界条件的选择见参考文献[13]。其中对于其硅基固体壁，其速度边界条件设定为无滑移、无渗透。对于流体，设定统一的入口条件，流道出口设定为常压。
对于无滑移的壁面条件，壁面和流体交界处的流动特性被用于预测壁面处流体的切向应力[13]。在层流模型中，这种流动特性的计算依赖于壁面处速度梯度的分布。由于本文中所模拟的微通道热沉采用的是层流模型，热沉中通道壁处的切向应力τf可由速度梯度的变化来表示:
${{\rm{ \mathit{ τ} }}_{\rm{f}}} = \mathit{\mu }\left( {\frac{{\partial \mathit{u}}}{{\partial \mathit{n}}}} \right) $
(1) 利用傅里叶定律来计算微通道内壁和接触流体表面的热交换公式为：
$ - {\mathit{\kappa }_{\rm{f}}}\left( {\frac{{\partial {T_{\rm{f}}}}}{{\partial n}}} \right) = - {\kappa _{\rm{s}}}\left( {\frac{{\partial {T_{\rm{s}}}}}{{\partial n}}} \right) $
(2) 式中，Tf和Ts分别表示热沉中流体和固体的温度，κf和κs分别代表流体和固体的导热系数，μ为流体的粘度系数，u代表微通道中流体的速度，n表示垂直于壁面的局部坐标。
为了计算本文中优化矩形凹槽结构微通道热沉的流固耦合传热，有限体积法(finite volume method，FVM)和混合差分方案被采用，对流、固体部分的离散方程求解，工质的流动选择了Simple算法，同时运用2阶迎风格式迭代，能量方程则使用了Quick格式迭代。压力插值采用了标准格式。在收敛判据方面，当进出口质量基本守恒，残差小于10-3，动量和能量方程的残差小于10-7时，可以视计算结果已经收敛。
微通道热沉底部加载均匀热流密度q=106W/m2，流、固接触面设定为耦合边界条件，流道入口处的水温设置为300K，热沉固体部分材料选用硅，其比热容为712J/(kg·K)，导热系数为148W/(m·K)，密度为2329kg/m3。图 2a和图 2b中计算域的两侧面设置为对称面，其它外表面设置为绝热面。
-
为了显示更多的换热细节，得到更高的计算精度，本文中所有的计算域中的模型采用了结构化的六面体网格并用ICEM对其划分。文中所有的计算模型都对其网格进行了独立性验证。例如，对优化结构带凹槽的微通道热沉模型(s=0mm, P=0.2mm, θ=45°)，设定入口速率为4m/s, 热沉底部热流密度q=106W/m2，入口水温300K。分别运用4种不同密度的网格分别计算微通道进出口的压差和流体工质的平均温度，从而验证传热和流体流动两方面计算的准确性。这里使用下式来[14]表述各种不同网格设置条件下微通道进出口压差和流体工质的平均温度的差值:
$E\% = \left| {\frac{{{f_2} - {f_1}}}{{{f_1}}}} \right| \times 100 $
(3) 式中，f1，f2分别代表相邻两种网格设置条件下的压差或平均温度。表 3中给出了具体的差值。从表 3可以看出，在99×104和105×104两种网格设置的条件下，压差和平均温度的差值分别是0.8%和0.75%，这两个值都小于1%，所以可以认定这两种网格设定条件下的计算值是准确的。由于考虑到更多数量的网格设定会耗费更多的计算资源，所以选择105×104网格作为优化结构带凹槽的微通道热沉模型(s=0mm, P=0.2mm, θ=45°)这一模型的计算。其它的模型均采用这种方式进行网格独立性的验证。图 4即为带优化结构凹槽的微通道热沉模型(s=0mm, P=0.2mm, θ=45°)的网格划分图。
Figure 4. Computational grid for solution domain of the microchannel with s=0mm, P=0.2mm, θ=45°
Table 3. Difference between inlet and outlet pressures and average temperature under different grid settings
grid/104 0.68~0.85 0.85~0.99 0.99~1.05 E(Δp)/% 25 5 0.8 E(Tave)/% 22 8 0.75 为了验证计算模型的可靠性，对传统直通型微通道结构(见图 2a)在给定相同初始条件的情况下，将数值模拟的结果和公式计算的结果进行了比对，结果证明了数值模拟的结果是可靠的。
对于流体流动特性的验证，采用了STEINKE和KANDLIKAR在参考文献[15]中所描述的基于层流模型的传统直通型微通道结构入口出口压降Δp的公式。对于换热特性的验证，采用了PHILLIPS在参考文献[16]中所给出的计算努赛尔数Nu(x)的公式。数值计算和经验公式的比对如图 5和图 6所示。从图中可以看出, 数值计算与公式计算，两者的结果能很好地符合。因此采用相同的方法，对本文中其它流道结构的热沉，采用同样的方法进行数值计算，其输出数据是有效的。
$\Delta \mathit{p = }\frac{{2\left( {f\mathit{Re}} \right)\mathit{\mu }{\mathit{u}_{\rm{m}}}L}}{{{D_{\rm{h}}}^2}} + K\frac{{\mathit{\rho }{\mathit{u}_{\rm{m}}}^2}}{2} $
(4) 
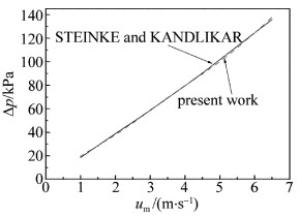
Figure 5. Comparison of present work and STEINKE and KANDLIKAR[15] for Δp
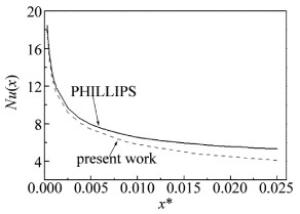
Figure 6. Comparison of present work and PHILLIPS[16] for Nu(x)
式中, um是截面处的平均速率，Dh表示流道的水力直径，L是流道的长度，αc为流道的宽高比，Re代表雷诺数，Pr是普朗特数，f为摩擦因子，K为比例系数，ρ为密度。
$\begin{array}{l} f\mathit{Re = 96}{\rm{(}}1 - 1.3553{\mathit{\alpha }_{\rm{c}}} + 1.9467{\mathit{\alpha }_{\rm{c}}}^2 - \\ 1.7012{\mathit{\alpha }_{\rm{c}}}^3 + 0.9564{\mathit{\alpha }_{\rm{c}}}^4 - 0.2537{\mathit{\alpha }_{\rm{c}}}^5) \end{array} $
(5) $\begin{array}{l} K{\rm{ = }}0.6797 + 1.2197{\alpha _{\rm{c}}} + 1.9467{\alpha _{\rm{c}}}^2 - \\ 9.5921{\alpha _{\rm{c}}}^3 + 8.9089{\alpha _{\rm{c}}}^4 - 2.9959{\alpha _{\rm{c}}}^5 \end{array} $
(6) $\begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;Nu\left( x \right) = \\ 1.0958\left( {\frac{{23.315 + 27038{x^*} + 1783300{x^{*2}}}}{{1 + 3049{x^*} + 472520{x^{*2}} - 35714{x^{*3}}}}} \right) \end{array} $
(7) ${\mathit{x}^*} = \frac{x}{{{D_{\rm{h}}} \cdot \mathit{Re} \cdot \mathit{Pr}}} $
(8) -
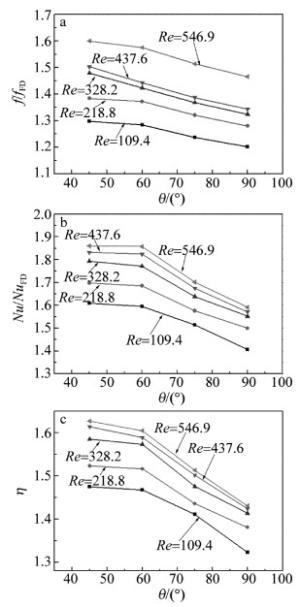
图 7中研究了当P=0.2mm、s=0mm、热沉底部热流密度q=106W/m2、微通道入口处的温度为Tin=300K条件下，凹槽倾斜角度θ对热沉换热性能影响。图 7a中给出了优化结构矩形凹槽流道摩擦因子f与直通型流道摩擦因子fFD的比值f/fFD在不同流速下随θ参量的变化关系。从图 7a中可以看出, 在θ从90°变化到60°的过程中, f/fFD的增长率要大于θ从60°变化到45°的过程中f/fFD的增长率。这主要是因为随着θ从90°变化到45°，微通道中凹槽收缩面与流体的摩擦面积在不断的增大；同时收缩面与微通道主流方向的夹角逐渐扩大，流体质点速度变化剧烈，产生漩涡的强度越来越大并冲击收缩壁面，使摩擦系数不断升高，但随着θ不断地减小，到达一定的值后，收缩壁面离扩张段的平均距离增加，漩涡冲击收缩壁面的强度逐渐下降，使相对摩擦因子f/fFD的增长率开始下降。
Figure 7. Relationship between some parameters and θ at different Reynoids numbers Re
图 7b中给出了优化结构矩形凹槽微通道热沉努赛尔数Nu与直通型微通道努赛尔数NuFD的比值Nu/NuFD在不同流速下随参量θ的变化关系。从图中可以看出, Nu/NuFD随θ的变化与f/fFD随θ的变化，两者趋势相同。当θ从90°变化到60°，Nu/NuFD的增长率较大，一方面随着θ的减小，凹槽的换热面积在增加；另一方面收缩壁面面积的扩大，流体质点速度变化剧烈，产生的强烈漩涡在收缩段能够得到有效的利用。当θ从60°变化到45°，Nu/NuFD的增长率下降，这是因为凹槽区层流范围扩大，导致其换热系数相对下降。同时从图 7b可以看出, 当倾斜角度θ优化为45°时, 散热效率相比较直通型热沉提高了60%。
图 7c中还给出了优化结构矩形凹槽微通道热沉综合传热因子η在不同流速下随参量θ的变化关系。可以看出, 优化结构矩形凹槽结构的综合传热性能远好于直通型结构。θ=45°时有最优化换热效果。
-
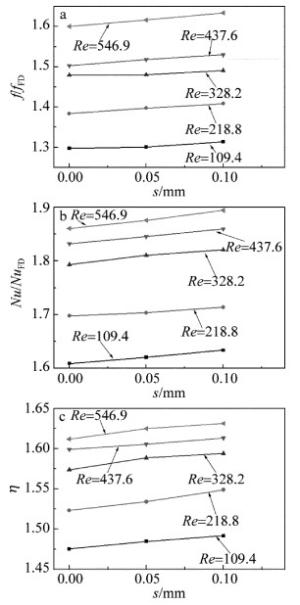
图 8中研究了当P=0.2mm、θ=45°，同时热沉底部热流密度q=106W/m2、微通道入口处的温度为Tin=300K条件下，凹槽交错距离s对热沉换热性能影响。s参量反映了微通道内左凹槽壁、右凹槽壁交错的距离。图 8a中给出了优化结构矩形凹槽微通道热沉摩擦因子f与直通型微通道摩擦因子fFD的比值f/fFD在不同流速下随s参量的变化关系。从图 8a中可以得到随着Re的增加，f/fFD在缓慢的变大，同时随着s的增加，f/fFD也有增大的趋势。因为一方面由于凹槽壁面结构的影响，微通道内的流体除了主流动方向上的速度还会产生一个与主流动方向垂直的速度分量，从而会造成流道内阻力的上升；另一方面随着Re的增加，流体质点速度变化加剧，会产生更加剧烈的漩涡，使f/fFD的值不断增加。
Figure 8. Relationship between some parameters and s at different Reynolds numbers Re
图 8b中给出了优化结构之后热沉的努赛尔数Nu与直通型微通道努赛尔数NuFD的比值Nu/NuFD在不同流速下随参量s的变化关系。由于较高的压降会导致较高的对流换热系数，从图中可以看出Nu/NuFD和f/fFD在s变化时有相同的趋势。这说明通过提高微通道热沉的进口流速提高压降能够在一定程度上增加系统的对流换热。从图中还可以看出当s从0mm变化到0.1mm的过程中，Nu/NuFD也是一个增大的过程。这是因为流道中周期性凹槽部分的喷射节流效应会使得此区域的热边界层出现中断和再发展，加强换热；同时左右凹槽非对称的分布，流体工质在流道的扩张段所产生的较大尺寸漩涡在进入流道凹槽收缩段时会使得流体流速增加并且其层流底层变薄，这些都有对加强传热有好处。从图 8b可以看出, 交错优化后的结构散热效率相比较直通型热沉提高了60%以上。
图 8c中还给出了优化结构矩形凹槽微通道热沉综合传热因子η在不同流速下随参量s的变化关系。从图中可以看出, s=0.1mm时有最优化换热效果。
-
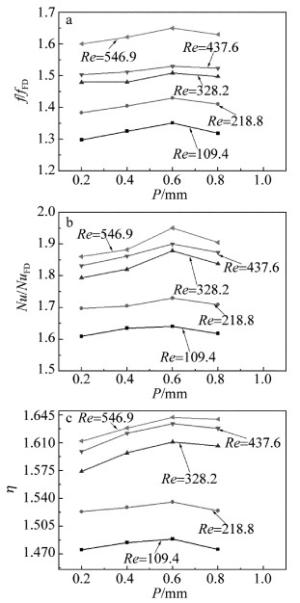
图 9中研究了当s=0mm、θ=45°、同时热沉底面热流密度q=106W/m2、微通道入口处的温度为Tin=300K条件下，凹槽间距P对热沉换热性能影响。图 9a中给出了优化结构矩形凹槽微通道热沉摩擦因子f与直通型微通道摩擦因子fFD的比值f/fFD在不同流速下随P参量的变化关系。从图中可以看出, 在P从0.2mm变化到0.6mm时，f/fFD在不断增大；当P从0.6mm变化到0.8mm时，f/fFD开始减小。这说明优化结构矩形凹槽微通道内流体流动与传热的影响不仅与单个凹槽的结构有关，更重要的是与凹槽的间距也有很大的关系。随着P值的增加，等截断面的间距也在增加，因此流体边界层会从开始的没有足够的空间发展变化到完全发展状态，当P=0.6mm时, f/fFD也达到一个峰值；当P值继续增加时，为流体保持完全发展状态提供了更多的空间，f/fFD值也开始下降。
图 9b中给出了优化型矩形凹槽微通道热沉努赛尔数Nu与直通型微通道努赛尔数NuFD的比值Nu/NuFD在不同流速下随参量P的变化关系。从图中可以看出, Nu/NuFD随P值的变化有一个先增长后减小的过程。同时从图 9b可以看出, 优化后的结构散热效率相比较直通型热沉提高了60%以上。因此可以表明存在一个最佳的凹槽间距为热沉提供换热。凹槽之间的距离过小，会减少热边界层的重新发展，这样会使得对流换热系数降低，弱化热沉整体的换热效果。凹槽之间的距离合适时，微通道中的流体通过凹槽扩张段进口喷射冲击扩张壁面在凹槽内部有足够的空间进行冷热流体的有效混合，这可以促进对流换热系数的提高。
Figure 9. Relationship between some parameters and P at different Reynolds numbers Re
图 9c中还给出了优化结构矩形凹槽微通道热沉综合传热因子η在不同流速下随参量P的变化关系。从图中可以看出, P=0.6mm时有最优化换热效果。
通过数值模拟得到的热沉最优化参量，实际加工制造后加载在激励源上并将激励源安装至4kW轴快流CO2激光器，连续运行5h。激光输出功率稳定度如表 4所示。由此可以得出经过优化后的热沉完全能够满足激光器的工作需要。
Table 4. power & temperature
time output power/kW surface temperature of power MOSFET/K 13:00 4.01 339 14:00 4.02 340 15:00 4.02 339 16:00 3.99 340 17:00 3.98 340 18:00 4.02 342 output power stability < ±2% -
本文中提出了一种新型的激光器激励源热沉微通道结构，采用计算流体动力学的方法对热沉结构进行了优化设计。
(1) 对于热流密度为106W/m2、面积为16cm2的激励源热沉，优化之后的结构完全能够保证热流密度为106W/m2情况下，热沉表面温度低于340K，满足MOSFET工作时对温度的要求。
(2) 由于换热面积的增加和凹槽中更大漩涡的形成，随着几何参量θ的减小和s的增加，微通道热沉的整体换热性能都会有所提升；微通道中存在一个最佳的P值为边界层的重新发展提供合适的空间；对于优化之后的凹槽微通道热沉最佳的几何尺寸分别是θ=45°, P=0.6mm和s=0.1mm。
高功率轴快流CO2激光器激励源热沉结构优化设计
Optimization design of microchannel heat sinks of excitation sources for high power fast axial flow CO2 lasers
-
摘要: 为了提高激励源的热稳定性，保证4kW轴快流CO2激光器的光束质量，采用计算流体动力学的方法，理论分析了激光器激励源热沉的散热机理，对热流密度为106W/m2、面积为16cm2的激励源热沉结构进行了优化设计。结果表明，经过优化之后的热沉其表面的最高温度低于340K，完全能够满足激光器正常工作时激励源核心功率MOSFET对散热指标的要求；同时经过数值模拟得到了带凹槽微通道热沉的优化结构尺寸，分别是微通道凹槽间距P=0.6mm，微通道凹槽倾角θ=45°，微通道凹槽交错距离s=0.1mm，同时当雷诺数Re=546.9时，热沉有最优的散热效果，激光输出功率的稳定度可以控制在±2%以内。此研究为设计具有高效散热能力的微通道热沉提供了理论指导。Abstract: In order to improve the thermal stability of excitation sources and ensure the beam quality of 4kW axis fast flow CO2 laser, the thermal dissipation mechanism of heat sinks of laser excitation sources theoretically was analyzed by means of computational fluid dynamics method. The heat sink structure of the excitation source with heat flux of 106W/m2 and area of 16cm2 was optimized. The results show that the maximum temperature on the surface of the heat sink is lower than 340K after optimization. It can fully meet the requirements of the heat source of MOSFET which is the core power of the excitation source in the normal operation of the laser. At the same time, by numerical simulation, the optimal structure size of the microchannel heat sink is obtained. The channel spacing P is 0.6mm, microchannel groove angle θ is 45°, and channel spacing s is 0.1mm. When the Reynolds number is Re=546.9, the heat sink has the best cooling effect. And the stability of laser output power can be controlled within ±2%. This study provides the theoretical guidance for the design of microchannel heat sinks with high heat dissipation capability.
-
Key words:
- lasers /
- heat sink /
- numerical simulation /
- cooling effect
-
Figure 1. a—structural schematic of a fast axial flow CO2 laser b—structure of a heat sink assembly
Figure 2. Schematic diagram and detailed view of the computational domain
a—for MCHS b—for RGMCHS
Figure 4. Computational grid for solution domain of the microchannel with s=0mm, P=0.2mm, θ=45°
a—for solid b—for fluid
Figure 7. Relationship between some parameters and θ at different Reynoids numbers Re
a—flow performance f/fFD b—thermal performance Nu/NuFD c—efficiency η
Figure 8. Relationship between some parameters and s at different Reynolds numbers Re
a—flow performance f/fFD b—thermal performance Nu/NuFD c—efficiency η
Figure 9. Relationship between some parameters and P at different Reynolds numbers Re
a—flow performance f/fFD b—thermal performance Nu/NuFD c—efficiency η
Table 1. Variables of the wall channel
the fixed value variables P=0.2mm, s=0mm θ=90°, 75°, 60°, 45° θ=45°，s=0mm P=0.2mm, 0.4mm, 0.6mm, 0.8mm θ=45°，P=0.2mm s=0mm, 0.05mm, 0.1mm 
下载: 导出CSV
Table 3. Difference between inlet and outlet pressures and average temperature under different grid settings
grid/104 0.68~0.85 0.85~0.99 0.99~1.05 E(Δp)/% 25 5 0.8 E(Tave)/% 22 8 0.75
下载: 导出CSV
Table 4. power & temperature
time output power/kW surface temperature of power MOSFET/K 13:00 4.01 339 14:00 4.02 340 15:00 4.02 339 16:00 3.99 340 17:00 3.98 340 18:00 4.02 342 output power stability < ±2%
下载: 导出CSV
-
[1] LI Q, WANG Y Q, HUANG H Y. Progress of numericalsimulation of high power fast-axial-flow CO2 lasers [J]. Laser Technology, 2010, 34(3): 339-342(in Chinese). [2] LI J J, LI B, WANG Y Q. Comparative analysis of discharge tube of CO2 lasers with large mass flow rate and fast-axial flow [J]. Laser Technology, 2015, 39(3): 308-311(in Chinese). [3] TUCKERMAN D B, PEASE R F W. High-performance heat sinking for VLSI[J]. IEEE Electron Device Letters, 1981, 2(5): 126-129. doi: 10.1109/EDL.1981.25367 [4] QU W L, MUDAWAR L. Analysis of three-dimensional heat transfer in micro-chanel heat sinks[J]. International Journal of Heat and Mass Transfer, 2002, 45(19): 3973-3985. doi: 10.1016/S0017-9310(02)00101-1 [5] ZHOU J J, SHEN Sh, XU J L, et al. Single-phase flow and heat transfer in micro-channels [J].Journal of Chemical Industry and Engineering, 2005, 56(10): 1849-1855(in Chinese). [6] HEE S P, JEFF P. Friction factor and heat transfer in multiple microchannels with uniform flow distribution [J]. International Journal of Heat and Mass Transfer, 2008, 51(17/18): 4535-4543. [7] KANDLIKAR S G, UPADHYE H R. Extending the heat flux limit with enhanced microchannels in direct single-phase cooling of computer chips [C]// Twenty First Annual IEEE-Semiconductor Thermal Measurement and Management Symposium.New York, USA: IEEE, 2005: 8-15. [8] LI Z G, HUAI X L, TAO Y, et al. Effects of thermal property variations on the liquid flow and heat transfer in microchannel heat sinks [J]. Applied Thermal Engineering, 2007, 27(17): 2803-2814. [9] HEINZ H, SHRIPAD P. Variable property effects in single-phase incompressible flows through microchannels [J]. International Journal of Thermal Sciences, 2006, 45(10): 977-981. doi: 10.1016/j.ijthermalsci.2006.01.002 [10] GIUDICE S D, NONINO C, SAVINO S. Effects of viscous dissipation and temperature dependent viscosity in thermally and simultaneously developing laminar flows in microchannels [J]. International Journal of Heat and Fluid Flow, 2007, 28(1): 15-27. doi: 10.1016/j.ijheatfluidflow.2006.05.007 [11] VANAKI S M, GANESAN P, MOHAMMED H A. Numerical study of convective heat transfer of nanofluids: A review [J]. Renewable and Sustainable Energy Reviews, 2016, 54:1212-1239. doi: 10.1016/j.rser.2015.10.042 [12] MOHAMMED H A, GUNNASEGARAN P, SHUAIB N H. Heat transfer in rectangular microchannels heat sink using nanofluids [J]. International Communications in Heat and Mass Transfer, 2010, 37(10):1496-1503. doi: 10.1016/j.icheatmasstransfer.2010.08.020 [13] XIA G, CHAI L, WANG H, et al. Optimum thermal design of microchannel heat sink with triangular reentrant cavities [J]. Applied Thermal Engineering, 2011, 31(6/7): 1208-1219. [14] GUO J F, XU M T, CHENG L. Second law analysis of curved rectangular channel [J]. International Journal of Thermal Sciences, 2011, 50(5):760-768. doi: 10.1016/j.ijthermalsci.2010.12.011 [15] STEINKE M E, KANDLIKAR S G. Single-phase liquid friction factors in microchannels [J]. International Journal of Thermal Sciences, 2006, 45(11):1073-1083. doi: 10.1016/j.ijthermalsci.2006.01.016 [16] PHILLIPS R J. Microchannel heat sinks.Advances in Themal Modeling of Electronic Components and Systems, 1990, 2:109-184. -
点击查看大图
计量
- 文章访问数: 3526
- HTML全文浏览量: 1879
- PDF下载量: 254
- 被引次数: 0
