网站地图
-
高光谱遥感图像具有较高的光谱分辨率，它被广泛地应用于地物分类和目标识别，但其较大的信息冗余和庞大的数据也给计算带来了一定的困难，这就需要在既不丢失重要信息又能保留原始数据物理属性的情况下，尽量降低数据的维数。波段选择就是高光谱图像处理过程中的一个关键环节[1-3]，其目的是去除原始数据中的冗余信息。
常见的高光谱图像的波段选择算法有：LIU等人提出的自适应波段选择算法，用每个波段的标准差与相邻波段相关系数的比值作为每个波段的指数，并依据指数的大小来选择波段[4]。MEDJAHED等人[5]和SU等人[6]提出了启发性优化类算法。FENG等人[7]和HOSSAIN等人[8]提出了基于互信息的波段选择算法。SU等人[9]提出粒子群优化算法，将选择波段及确定所选波段的最佳数目同时进行。SUN等人[10]提出改进的稀疏子空间聚类算法，先假定波段向量是联合低维正交子空间的采样点，每个波段在其子空间中都可被其他波段线性稀疏表示，然后进行后续计算。WANG等人[11]提出结合遗传算法和蚁群算法的波段选择方法，先利用遗传算法获得几组较优解，并用它来初始化蚁群算法，进而得到较优波段组合。以上算法大部分是以聚类思想为基础的，通过两两波段之间的相似性进行聚类，再进一步剔除每个类中的相应波段，而没有充分考虑多个波段之间的线性关系。
基于以上分析，作者提出了一种新的算法，即基于波段指数的波段选择算法。该算法先用小波变换对高光谱图像数据进行去噪处理，然后针对余下的所有波段，计算出它们的联合偏度与峰度指数，根据一定的条件将其分成两组，最后再根据波段指数的大小确定相对较小指数的波段，并将其作为冗余波段进行去除，从而得到最小波段集。
-
偏度与峰度分别代表了随机变量分布的不对称程度和密度函数的起伏程度，它们能较好地反映图像的非正态特性，在度量图像的相似性方面非常适用。为了更好地反映数据偏离正态分布的程度，将偏度与峰度系数的乘积作为衡量偏离程度的指标，也即联合偏度与峰度指数，用F表示:
$ F = S \cdot K $
(1) 式中，S表示变量的偏度，K表示变量的峰度。
设总体x的一个样本为x1, x2, …, xm。因此，偏度的离散形式是：
$ \hat S = \frac{{\frac{1}{m}\sum\limits_{i = 1}^m {{{({x_i} - \bar x)}^3}} }}{{{{\left[ {\frac{1}{m}\sum\limits_{i = 1}^m {{{({x_i} - \bar x)}^2}} } \right]}^{3/2}}}} $
(2) 峰度的离散形式是：
$ \hat K = \frac{{\frac{1}{m}\sum\limits_{i = 1}^m {{{({x_i} - \bar x)}^4}} }}{{{{\left[ {\frac{1}{m}\sum\limits_{i = 1}^m {{{({x_i} - \bar x)}^2}} } \right]}^2}}} - 3 $
(3) 式中，样本的平均值为$ \bar x = \frac{1}{m}\sum\limits_{i = 1}^m {{x_i}} $。
为了方便计算，转化二者的乘积，即得到F的离散公式：
$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;F = \hat S \cdot \hat K{\rm{ = }}\\ \;\left\{ {\frac{1}{m}\sum\limits_{i = 1}^m {{{({x_i} - \bar x)}^3}} {{\left[ {\frac{1}{m}\sum\limits_{i = 1}^m {{{({x_i} - \bar x)}^2}} } \right]}^{2/3}}} \right\} \cdot \\ \left\{ {\frac{1}{m}\sum\limits_{i = 1}^m {{{({x_i} - \bar x)}^4}} {{\left[ {\frac{1}{m}\sum\limits_{i = 1}^m {{{({x_i} - \bar x)}^2}} } \right]}^{1/2}} - 3} \right\} \end{array} $
(4) 经过分析可知，F值越小，数据偏离正态分布的程度越小，包含信息越少，因此，其值的正负代表了不同的数据分布。
-
设高光谱数据的波段数为L，每个波段影像所含像元个数均为M×N，第l个波段像元灰度值为al, q, t(l=1, 2, …, L; q=1, 2, …, M; t=1, 2, …, N)。参考文献[13]和参考文献[14]中均提到了该方法，设Rij是波段i与j之间的相关系数，高光谱数据被分成t组，每组的波段数分别为n1, n2, …, nt。波段指数公式为：
$ {P_i} = \frac{{{\sigma _i}}}{{{R_i}}} $
(5) $ {R_{ij}} = \frac{{\sum\limits_{q = 1}^M {\sum\limits_{t = 1}^N {\left( {{a_{i, q, t}} - {{\bar a}_i}} \right)\left( {{a_{j, q, t}} - {{\bar a}_j}} \right)} } }}{{\sqrt {\sum\limits_{q = 1}^M {\sum\limits_{t = 1}^N {{{\left( {{a_{i, q, t}} - {{\bar a}_i}} \right)}^2}} } } \sqrt {\sum\limits_{q = 1}^M {\sum\limits_{t = 1}^N {{{\left( {{a_{j, q, t}} - {{\bar a}_j}} \right)}^2}} } } }} $
(6) $ {\sigma _i} = \sqrt {\frac{{\sum\limits_{q = 1}^M {\sum\limits_{t = 1}^N {{{\left( {{a_{i, q, t}} - {{\bar a}_i}} \right)}^2}} } }}{{M \times N}}} $
(7) 式中，Ri=R1+R2，$ {R_1} = \frac{1}{{{n_k}}}\sum\limits_{j = 1}^{{n_k}} {\left| {{R_{ij}}} \right|\left( {i \ne j} \right)} $，R1是第i个波段与所在组内其它波段之间相关系数的绝对值之和的平均值，R2是第i个波段与所在组外的其它波段之间相关系数的绝对值之和, σi是第i个波段的标准差，ai, aj分别为第i, j波段的影像像元的平均灰度值。由以上式子可以看出，它包含了波段的信息量和相关性两方面的信息。相关系数绝对值越大的波段，其信息冗余度越大；而标准差越小的波段，其所含的信息量越少。
-
由于高光谱数据具有波段数目多、信息冗余度高、相关性强等特点，因而增加了数据的处理难度。为了更有效地利用高光谱数据的丰富信息，选出最优的波段子集，现将联合偏度与峰度和波段指数法相结合进行波段选择。根据文中波段指数的公式和定义可知，阈值的选取可以根据后续处理的需要选择合适的波段指数值，进而选出波段指数排在前面的n个波段。
算法的具体步骤如下：
(1) 输入：高光谱图像数据，其中数据的每一个行向量代表一个对应的波段；S={1, 2, …, L}，阈值α。
(2) 输出：波段选择结果集S。第1步：用小波变换[15-16]对高光谱图像数据进行去噪处理，先用各波段图像小波子带的熵来估计出噪声的大小，再进行排序，进而把一定量噪声较大的波段去掉[17]，此时波段集为S1$ \subset $S，转第2步; 第2步：分别计算波段集S1中波段的图像数据所对应的F值，再根据F值的正负将所有波段进行划分，分为两组，转第3步; 第3步:对所有i∈S1，在分成的两组波段之间，用(5)式进行计算，如果Pi < α，则S=S1－{i}，若Pi > α，则保留第i个波段；输出S，算法结束。
-
为了证明本文中所提出的算法是有效的，设计了两组实验，在实验中小波变换部分均采用的小波基是Haar小波，并选择了Haar小波的一层分解。其中一组实验以美国内华达州Cuprite地区的AVIRIS数据为研究对象，利用全波段和使用本文方法选出的波段分别提取端元，并把端元的位置在图中标记; 另一组以美国印第安纳州的Indian pines高光谱数据为研究对象，分别在全波段下和利用本文中的方法选出的波段下计算分类精度。
-
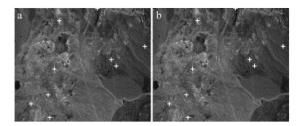
Cuprite地区AVIRIS原始数据共有224个光谱波段，10nm的光谱分辨率，尺寸为512×614像元。本文中删除了噪声较大和光谱吸收较大的波段，选择172~221光谱区间的50个波段用于算法测试。为了满足实验需要，将波段指数按从大到小排序后的第21个波段指数值作为阈值，取阈值α=0.1755，此时由本文中算法所选择的波段数目为20，用参考文献[18]中端元提取的方法，分别对全波段及去波段后的数据进行端元提取实验，实验结果如图 1所示。
Figure 1. Location map of the endelement
通过对比图 1中的两幅图可知，两图中的端元位置是一致的，也即按照本文中所提出的算法选出的波段提取的端元与在全波段下提取的端元是相同的，说明所选的端元是精确的。图中的端元位置坐标分别为：(2，374)，(58，202)，(174，588)，(233，437)，(262，459)，(276，180)，(392，152)，(433，75)，(495，159)。
-
实验中所用的数据为美国印第安纳州的Indian pines高光谱数据，该数据有220个波段，波长范围是0.4μm ~2.5μm，光谱分辨率是10nm，空间分辨率是17m；实验中所用的图像大小为145×145，去除水吸收波段104~108, 150~163和220，用剩余的200个波段进行波段选择，用本文中算法选择出36个波段，然后采用K近邻(K-nearest neighbor, KNN)分类算法进行分类实验，实验结果如表 1所示。
Table 1. Classification results of KNN classifier
band selection method overall classification accuracy average classification accuracy kappa coefficient all band 0.7392 0.7437 0.7012 algorithm in this paper 0.7415 0.7253 0.7044 从表 1中本文中算法与全波段算法的精度对比可以看出，本文中算法所得精度较接近全波段下的精度，从而验证了本文中方法的准确性和有效性。
由两组实验结果的对比和分析可知，使用本文中算法选出的数量较少的波段得到的端元位置与使用全波段得到的端元位置相同，并且二者的分类精度也非常接近，说明实验达到了较好的效果，证明了该算法的可行性与有效性，为高光谱影像的进一步研究提供了新的思路。
-
本文中提出了基于波段指数的高光谱影像波段选择算法。该算法同时考虑波段间的相关性与信息量的大小等因素，提出利用联合峰度与偏度和波段指数相结合进行波段选择的新思路，克服了仅仅计算波段间相关性的不足之处，有效提高了计算精度。本文中设计的两组实验均达到了较好的效果，验证了该算法在波段选择过程中的可行性与有效性。因此，文中提出的基于波段指数的波段选择算法为降低高光谱影像维数提供了一种帮助。
基于波段指数的高光谱影像波段选择算法
Band selection algorithm for hyperspectral images based on band index
-
摘要: 为了去除高光谱影像的数据冗余，提高高光谱影像处理的精度和效率，提出了一种基于波段指数的高光谱影像波段选择算法。采用小波变换对高光谱图像数据进行去噪处理，依据联合偏度-峰度指数将波段进行分组，再根据波段指数的大小确定相对较小指数的波段，并将其作为冗余波段进行去除，从而得到最小波段集。结果表明，利用该波段集和全波段所选的端元是一致的，在不影响端元提取的前提下，最大程度地去除了冗余波段，而且该波段集与全波段的分类精度较接近。该算法在波段选择过程中具有可行性与有效性，为降低高光谱影像维数提供了一种帮助。Abstract: In order to remove data redundancy of hyperspectral images, and improve the accuracy and efficiency of hyperspectral image processing, a band selection algorithm was proposed based on band index of hyperspectral images. Wavelet transform was used to deal with the noise of hyperspectral image data. Bands are divided into groups by using joint skewness-kurtosis figure, and the band was removed as a redundant band which was determined based on the size of band index. The set of the minimum bands was obtained in this way. The experimental results show that the endmember set selected by using the above bands is consistent with that selected by using all bands. The redundancy band is removed to the greatest extent without affecting the endmember extraction. The classification accuracy of the band set is close to that of all bands. The band selection algorithm is feasible and effective. The study provides help to reduce the dimension of hyperspectral images.
-
Figure 1. Location map of the endelement
a—all bands b—the selected bands in this paper
Table 1. Classification results of KNN classifier
band selection method overall classification accuracy average classification accuracy kappa coefficient all band 0.7392 0.7437 0.7012 algorithm in this paper 0.7415 0.7253 0.7044 
下载: 导出CSV
-
[1] GONG M G, ZHANG M Y, YUAN Y. Unsupervised band selection based on evolutionary multiobjective optimization for hyperspectral images [J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(1):544-557. doi: 10.1109/TGRS.2015.2461653 [2] SUN K, GENG X R, JI L Y. A new sparsity-based band selection method for target detection of hyperspectral image[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(2):329-333. doi: 10.1109/LGRS.2014.2337957 [3] HE Y L, LIU D Z, WANG J L, et al. Independent component analysis-based band selection for hyperspectral imagery[J]. Infrared and Laser Engineering, 2012, 41(3):818-824(in Chinese). [4] LIU C H, ZHAO C H, ZHANG L Y. A new method of hyperspectral remote sensing image dimensional reduction[J]. Journal of Image and Graphics, 2005, 10(2):218-222. [5] MEDJAHED S A, SAADI T A, BENYETTOU A, et al. Gray wolf optimizer for hyperspectral band selection[J]. Applied Soft Computing, 2016, 40:178-186. doi: 10.1016/j.asoc.2015.09.045 [6] SU H J, YONG B, DU Q. Hyperspectral band selection using improved firefly algorithm[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(1):68-72. doi: 10.1109/LGRS.2015.2497085 [7] FENG J, JIAO L, ZHANG X, et al. Hyperspectral band selection based on trivariate mutual information and clonal selection[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(7):4092-4105. doi: 10.1109/TGRS.2013.2279591 [8] HOSSAIN M A, JIA X, PICKERING M. Subspace detection using a mutual information measure for hyperspectral image classification[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(2):424-428. doi: 10.1109/LGRS.2013.2264471 [9] SU H J, DU Q, CHEN G S, et al. Optimized hyperspectral band selection using particle swarm optimization[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(6):2659-2670. doi: 10.1109/JSTARS.2014.2312539 [10] SUN W W, ZHANG L P, DU B, et al. Band selection using improved sparse subspace clustering for hyperspectral imagery classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(6):2784-2797. doi: 10.1109/JSTARS.2015.2417156 [11] WANG L G, WEI F J. Band selection for hyperspectral imagery based on combination of genetic algorithm and ant colony algorithm [J]. Journal of Image and Graphics, 2013, 18(2):235-242(in Chinese). [12] GUO L, CHANG W W, FU C Y. Band selection of optimal for hyperspectral image fusion[J]. Journal of Astronautics, 2011, 32(2):374-379(in Chinese). [13] ZHAO C H, CHEN W H, YANG L. Research advances and analysis of hyperspectral remote sensing image band selection[J]. Journal of Natural Science of Heilongjiang University, 2007, 24(5):592-602(in Chinese). [14] SU H J, DU P J, SHENG Y H. Study on band selectional gorithms of hyperspectral image data[J]. Application Research of Computers, 2008, 25(4): 1093-1096(in Chinese). [15] CHEN S Y, LIU J X, DING Y. Study on fusion method of infrared and X-ray image based on wavelet transform[J]. Laser Technology, 2015, 39(5):685-688(in Chinese). [16] CHEN F, ZHANG W W, YU W J, et al. Fusion algorithm of EMCCD's low-light-level images based on wavelet transform[J]. Laser Technology, 2014, 38(2):155-160(in Chinese). [17] ZHOU Y, LI X R, ZHAO L Y. Modified linear-prediction based band selection for hyperspectral image[J]. Acta Optica Sinica, 2013, 33(8): 0828002(in Chinese). doi: 10.3788/AOS [18] GAO L R, GAO J W, LI J, et al. Multiple algorithm integration based on ant colony optimization for endmember extraction from hyperspectral imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(6):2569-2582. doi: 10.1109/JSTARS.2014.2371615 -
点击查看大图
图(1) / 表(1)
计量
- 文章访问数: 3558
- HTML全文浏览量: 1997
- PDF下载量: 250
- 被引次数: 0
