网站地图
下载:
-
新型2阶非线性光学材料的研究一直都是热点，尤其是探究高非线性系数、高损伤阈值、性能稳定性好的非线性材料。通过测量材料的非线性系数可以有效地判断其价值性。二次谐波法(second harmonic gene-ration, SHG)[1]以及Maker条纹法[2]经常适用于测量晶体的非线性系数，但这种方法要求样品有一定的尺寸以及高透过率。KURTZ等人[3]发展了测定晶体非线性特性的粉末倍频检测技术，之后加以改进提高准确率[4]。KLGUCHI等人[5]发展了弱信号倍频检测系统，能够检测到当相位匹配度低或折射率色散时产生的弱信号。LIU等人[6]实现了较大颗粒粉末倍频检测，并简化了实验条件。LI等人[7]改进了探测器，采用红外光学参量振荡器(optical parametric oscillator，OPO)激光以及把倍频光及其它光效应产生的光通过谱仪分光，结合CCD阵列探测器加以区分探测的新检测方案，提高了准确度。ARAMBURU等人[8]针对Kurtz理论的实际应用做了修正，深入研究了各种相位匹配材料和非相位匹配材料在不同颗粒尺寸的倍频信号输出情况。这些努力，使得粉末倍频检测技术成为探索非线性光学晶体材料的有效方法。
开展中、远红外材料(透过波长λ > 5000nm)的研究是目前2阶非线性光学材料研究的重点和前沿[9]，为了实现远红外的透过，这些材料往往采用硫属、硒属或磷属化合物[10]，其透光范围往往受到限制，如GaSe晶体(透光范围650nm~18000nm)、AgGaSe2晶体(710nm~18000nm)、4-甲基吡啶对甲基苯磺酸盐晶体(620nm~20000nm)等等[11]，如果采用常规的单一波长(1064nm)检测，其倍频检测信号(532nm)会被材料自吸收，探测器无法探测到其信号，因此本文中利用电光调Q光参量振荡器[12-13]获取的1064nm和1570nm双波长光源替代单一波长光源检测方式，利用波长1570nm的倍频信号(785nm)可以有效避免材料自吸收的特点，拓展了材料种类检测范围，尤其对红外材料的检测更有裨益。实验表明，粉末倍频检测系统能够有效地判断其是否具有非线性光学特性及效应的大小，验证结构设计的可靠性，为研究或改进新材料制备提供依据。
-
根据Kurtz-Perry晶体粉末倍频原理[3]，基频光为ω的光源对晶体粉末检测时得到2ω的倍频信号光，对于相位匹配材料和非相位匹配材料所探测到的理论值可以做如下表示。
(1) 相位匹配晶体粉末二次谐波强度：
$ \begin{array}{l} {I_{2\omega }} = \frac{{32{\rm{ \mathsf{ π} }}}}{c}{\left[ {\frac{{64{\rm{ \mathsf{ π} }}{I_\omega }}}{{\lambda {{({n_\omega } + 1)}^2}({n_{2\omega }} + 1)}}} \right]^2} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{d_{2\omega }}^2\left( {\frac{{{{\rm{ \mathsf{ π} }}^2}}}{4}L \mathit{\Gamma} } \right) \end{array} $
(1) $ {I_{2\omega }} \propto {d_{2\omega }}^2\left( {\frac{{{{\rm{ \mathsf{ π} }}^2}}}{4}L\mathit{\Gamma} } \right) $
(2) 式中，Γ=2lc(θ－θm)sinθm，且r$ \gg $Γ/sinθm, θ是入射角，θm为相位匹配角，lc表示相干长度，r为粉末颗粒平均半径，d2ω是相位匹配粉末材料有效非线性系数，c是光速，λ为基频光波长，Iω是基频光强度，nω和n2ω表示基频光和倍频光在材料中的折射率，L为样品厚度。
(2) 非相位匹配晶体粉末二次谐波强度：
$ \begin{array}{l} {I_{{\rm{n}}, 2\omega }} \approx \frac{{32{\rm{ \mathsf{ π} }}}}{c}{\left[ {\frac{{64{\rm{ \mathsf{ π} }}{I_\omega }}}{{\lambda {{\left( {{n_\omega } + 1} \right)}^2}\left( {{n_{2\omega }} + 1} \right)}}} \right]^2} \times \\ \;\;\;\;\;\;\;\;{d_{{\rm{n}}, 2\omega }}^2\left[ {L\frac{{{l_{\rm{c}}}^2}}{r}{\rm{si}}{{\rm{n}}^2}\left( {\frac{1}{2}{\rm{ \mathsf{ π} }}\frac{r}{{{l_{\rm{c}}}}}} \right)} \right] \end{array} $
(3) $ {I_{{\rm{n}}, 2\omega }} \propto {d_{{\rm{n}}, 2\omega }}^2\left[ {L\frac{{{l_{\rm{c}}}^2}}{r}{\rm{si}}{{\rm{n}}^2}\left( {\frac{1}{2}{\rm{ \mathsf{ π} }}\frac{r}{{{l_{\rm{c}}}}}} \right)} \right] $
(4) 式中, dn, 2ω为非相位匹配粉末材料有效非线性系数。
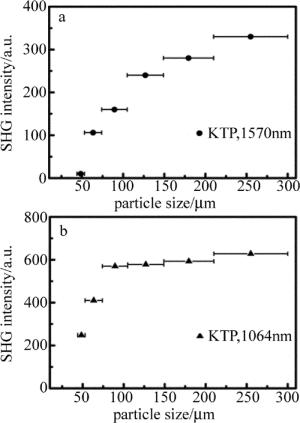
经计算，对于倍频信号强度与粉末颗粒度大小的关系如(2)式所示, 对于相位匹配粉末材料，r < 5lc倍频信号强度随着粒度增加而增加，在r=5lc时达到最大值，r > 5lc后基本保持不变。而对于非相位匹配粉末材料，见(4)式, 在r < 1.5lc时倍频信号强度随着粒径增加而增加，在r=1.5lc时达到最大值，当r > 1.5lc时，倍频信号强度随着粒子尺寸的增加反而减小。
-
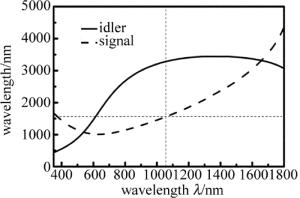
采用磷酸钛氧钾(KTP)晶体作为光参量振荡器(OPO)的变频晶体[14-15]，实验中采取Ⅱ类相位匹配。图 1中给出了KTP晶体在非临界相位匹配方向(入射角θ=90°, 波矢与x轴的夹角φ=0°)上OPO抽运光与信号光、闲频光的波长关系。由图中可知，当抽运光为1064nm时，KTP-OPO的信号光为1570nm。
Figure 1. KTP non-critical phase matching
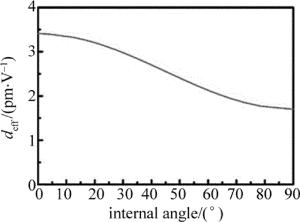
此时抽运光沿x轴传播，抽运光与信号光的偏振方向沿晶体y轴(o光)，空闲光偏振方向在x-z面(e光)，晶体有效非线性系数deff最大(如图 2所示)且无走离效应(走离角α=0mrad，如图 3所示)。
Figure 2. Curve of KTP effective nonlinear coefficient
Figure 3. Walkoff angle of KTP
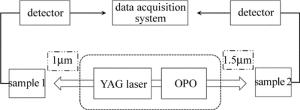
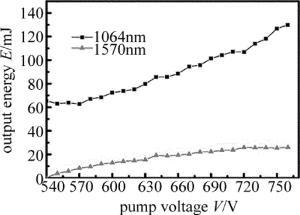
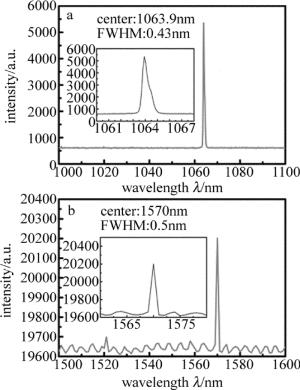
双波长粉末倍频实验装置如图 4所示。以纳秒Nd:YAG电光调Q激光器为抽运光源，以KTP晶体构建OPO，获得的激光光源波长为1064nm和1570nm，重复频率为1Hz，获取了130mJ@1064nm和20mJ@1570nm的双波长调Q激光输出，如图 5所示。光谱线宽为0.43nm@1064nm，0.5nm@1570nm，如图 6a和图 6b所示。在1064nm倍频的检测光路中样品1和探测器间放置吸收1064nm、透532nm的滤波片，同理在样品2和探测器间放置吸收1570nm、透785nm的滤波片，以尽量减小探测器噪声干扰。探测器采用光电倍增管，把光信号转换为电信号，采用数字示波器，进行电信号采集处理。
Figure 4. Schematic diagram of dual wavelength powder frequency doubling experiment
Figure 5. Dual wavelength energy output
Figure 6. Spectrogram of 1064nm output and 1570nm output
-
本实验的被测粉末样品为KTP，属于正双轴晶体，可透光谱范围350nm~4500nm，倍频相位匹配范围497nm~1800nm(type Ⅱ)。将测试样品分别放置在两个测试窗口测量，获得的测试结果如图 7所示。图 7中分别为1570nm与1064nm波长测试得到的KTP粉末不同颗粒度的倍频信号。由图可以看出，所测得的信号随颗粒度的增大而增强，然后趋于稳定，测试结果与Kurtz-Perry粉末倍频效应理论符合得很好，表明被测材料为相位匹配材料，这些实验结果与理论相符，证实了双波长粉末倍频检测系统的可靠性。由不同颗粒度信号强度估算得到系统的检测灵敏度达到0.17倍KTP有效非线性系数，即0.46pm/V。以已知非线性系数的KTP样品作为参照样品，系统可以用于测量其它材料的粉末倍频性能。以KTP样品的倍频信号强度作为标准信号强度，通过检测待测样品的倍频信号强度，与KTP标准信号强度进行对比，从而得出被测样品的非线性系数大小。
Figure 7. KTP crystal powder frequency doubling detection signal of 1570nm and 1064nm
-
基于Kurtz-Perry晶体粉末倍频理论，设计了1570nm和1064nm双波长粉末倍频检测装置，能够方便快捷地测出被测晶体粉末材料的倍频光信号，再通过对比标样KTP的标准信号强度，准确地判断被测晶体粉末材料的非线性倍频性能。该测试系统成本低、易于实现、检测速度快、稳定性高，能满足红外波段非线性光学材料的定性或是半定量检测，极大便利了非线性材料的研究工作。
双波长粉末倍频检测系统研究
Study on dual wavelength powder frequency doubling detection system
-
摘要: 为了测定粉末材料的倍频特性，根据Kurtz-Perry粉末倍频效应理论，采用光参量振荡技术，获取了130mJ@1064nm和20mJ@1570nm的双波长调Q激光输出，并进行了理论分析和实验验证。实现了粉末样品的1064nm和1570nm双波长倍频测试，解决了单一波长测试时晶体粉末材料对倍频信号波长的吸收而导致难以测得倍频信号的问题，有效非线性系数测试灵敏度达到0.46pm/V。结果表明，KTP粉末样品倍频信号变化趋势与理论相吻合，该系统对晶体的非线性检测运行稳定可靠，测试简单方便快捷。Abstract: In order to measure the frequency doubling characteristics of powder materials, according to the theory of Kurtz-Perry powder frequency doubling effect and the theory of optical parametric oscillation, dual wavelength Q-switched laser output of 130mJ@1064nm and 20mJ@1570nm was obtained. After theoretical analysis and experimental verification, the 1064nm and 1570nm dual wavelength frequency doubling test of powder sample was realized. The problem, that the absorption of crystal powder material to the wavelength of frequency doubling signal makes it difficult to measure the frequency doubling signal when testing the single wavelength, was solved. The results show that the test sensitivity of effective nonlinear coefficient reaches 0.46pm/V. the variation trend of frequency doubling signal of KTP powder samples is consistent with the theory. The system is stable, simple, convenient and reliable for nonlinear detection of crystals.
-
[1] NIKOGOSYAN D N. Nonlinear optical crystals: a complete survey[M]. Berlin, Germany: Springer Science & Business Media, 2006:403-405. [2] JERPHAGNON J, KURTZ S K. Maker fringes: a detailed comparison of theory and experiment for isotropic and uniaxial crystals[J]. Journal of Applied Physics, 1970, 41(4): 1667-1681. doi: 10.1063/1.1659090 [3] KURTZ S K, PERRY T T. A powder technique for the evaluation of nonlinear optical materials[J]. Journal of Applied Physics, 1968, 39(8): 3798-3813. doi: 10.1063/1.1656857 [4] DOUGHERTY J P, KURTZ S K. A second harmonic analyzer forthe detection of non-centrosymmetry[J]. Journal of Applied Crystallography, 1976, 9(2): 145-158. doi: 10.1107/S0021889876010789 [5] KIGUCHI M, KATO M, KUMEGAWA N, et al. Technique for eva-luating second-order nonlinear optical materials in powder form[J]. Journal of Applied Physics, 1994, 75(9): 4332-4339. doi: 10.1063/1.355976 [6] LIU G X, LU Y, JIN X. Study on an improved powder SHG technique[J]. Journal of Inner Mongolia Normal University(Natural Science Edition), 2009, 38(4): 407-410(in Chinese). [7] LI B X, WEI Y, HUANG C, et al. Research on testing the nonlinear optical performance of nonlinear optical materials based on the effect of second-harmonic generation[J]. Spectroscopy and Spectral Analysis, 2014, 34(1): 6-11. [8] ARAMBURU I, ORTEGA J, FOLCIA C L, et al. Second harmonic generation by micropowders: a revision of the Kurtz-Perry method and its practical application[J]. Applied Physics, 2014, B116(1): 211-233. [9] ZENG J B, CHEN H X, LIANG W G, et al. Research of optical pa-rametric oscillation of periodically poled MgO-doped LiNbO3 crystal[J]. Laser Technology, 2016, 40(3): 409-412(in Chines). [10] CHEMLA D S. Nonlinear optical properties of organic molecules and crystals[M].Amsterdam, Netnerlands: Amsterdam Elsevier, 2012:138-143. [11] KHOO I C, WU S T. Optics and nonlinear optics of liquid crystals[M].Singapour City, Singapour: Singapour World Scientific, 1993: 82-86. [12] PAN Y Sh, YAN Zh A, GUO W J, et al. Pulse laser injection seed-ed state detector and experimental research[J]. Laser Technology, 2016, 40(2): 153-156(in Chinese). [13] WANG B, REN G, LI T, et al. Experimental study of a kalium titanyl arsenate optical parametric oscillator in the mid-infrared band[J]. Laser Technology, 2007, 31(3): 225-227(in Chinese). [14] WANG L, WU X Y, LI Zh, et al. Progress of the nonlinear mid-infrared optical crystal and device of the parametric oscillator[J]. Laser Technology, 2011, 35(4): 434-439(in Chinese). [15] ZHENG Q, SUN J. Laser research of output wavelength controlled common aperture 0.532μm/1.064μm/3.9μm[J]. Laser Technology, 2017, 41(1): 10-13(in Chinese). -
点击查看大图
图(7)
计量
- 文章访问数: 3923
- HTML全文浏览量: 2371
- PDF下载量: 281
- 被引次数: 0
