网站地图
下载:
-
自20世纪中后期以来，随着激光加工技术的不断发展与改进，众多激光复合加工的方式陆续呈现在大众的视线之中，常见的激光复合加工技术有水导激光加工、水射流激光加工技术、超声辅助激光加工、激光诱导化学加工等[1-4]。同样的，随着计算机和流体数值分析技术的改进与发展，越来越多的科研人员利用计算机和流体分析软件能够准确、可靠、快速地分析出所需要的数据与结果。在激光复合加工的技术方面已有多位学者利用流体分析软件进行了研究。WANG等人对硅片弯曲的成形进行了数值的模拟和实验，指出了脆性材料的脉冲激光弯曲机理是有温度梯度机理和弯曲机理共同作用的结果[5]。ZHAN等人对水射流导引激光精密打孔的过程进行了分析，采用有限体积法建立了描述物理过程的数值模型，对打孔过程中熔池内部的流动和传热进行了模拟[6]。ZHANG等人研究了硅晶体激光直接刻蚀与水射流辅助激光复合加工刻蚀表面形貌，发现水射流与激光复合刻蚀能够有效去除重铸层并减少裂纹缺陷[7]。FU等人利用计算流体力学(computational fluid dynamics, CFD)的方法对水射流进行了气/液两相流数值模拟分析，研究了在不同速度下射流的破碎长度和射流破碎形式，同时还验证了缩流现象[8]。EDDIE对水射流激光加工进行了研究，探索射流速度与喷嘴直径之间对加工靶材的影响，并对射流速度和喷嘴直径优化[9]。
本研究是基于水辅助激光加工的机理，在水辅助激光加工中，水层流动特性是影响加工的一个重要因素，但是这方面的研究还很少。本研究通过对溶液辅助激光加工中的3种不同的水辅助激光流体装置，借助FLUENT流体分析软件，得到不同入口速度下，3种流体装置中流体的流动特性，这对水辅助激光加工中选取放置工件的位置，选取流体入口速度提供相关的理论依据[10-11]。
-
本文中所涉及到的为不可压缩连续流体、流体的黏壁效应、流体层流紊流速度的选择，故涉及到流体流动的连续性方程、伯努利方程和动量守恒方程，以及科安达效应和雷诺数的应用。
-
$ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho {\mathit{\boldsymbol{u}}})}}{{\partial x}} + \frac{{\partial (\rho {\mathit{\boldsymbol{v}}})}}{{\partial y}} + \frac{{\partial (\rho {\mathit{\boldsymbol{w}}})}}{{\partial z}} = 0 $
(1) 式中, ρ为流体的密度，t为时间，u, v, w为在x, y, z方向上的速度矢量[12]。
-
$ {z_1} + \frac{{{p_1}}}{{\rho g}} + \frac{{{\alpha _1}v_1^2}}{{2g}} = {z_2} + \frac{{{p_2}}}{{\rho g}} + \frac{{{\alpha _2}v_2^2}}{{2g}} + h $
(2) 式中, z1，z2表示在不同位置单位重量流体所具有的位能，几何意义为位置水头；p1，p2表示在不同位置单位重量流体所具有的压强；v1，v2表示不同位置流速；g, h分别表示重力加速度和水头损失。
-
考虑到水的粘性，在空间直角坐标系中，粘性不可压缩流体的动量守恒方程，即是纳维-斯托克斯方程(Navier-Stokes, N-S)方程[13]:
$ \left\{ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{u}}}}}{{\partial t}} + {\mathit{\boldsymbol{u}}}\frac{{\partial {\mathit{\boldsymbol{u}}}}}{{\partial x}} + {\mathit{\boldsymbol{u}}}\frac{{\partial {\mathit{\boldsymbol{u}}}}}{{\partial y}} + {\mathit{\boldsymbol{w}}}\frac{{\partial {\mathit{\boldsymbol{u}}}}}{{\partial z}} = \\ - \frac{{1\partial p}}{{\rho \partial x}} + \gamma (\frac{{{\partial ^2}{\mathit{\boldsymbol{u}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{\mathit{\boldsymbol{u}}}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{\mathit{\boldsymbol{u}}}}}{{\partial {z^2}}}) + {F_x}\\ \frac{{\partial {\mathit{\boldsymbol{v}}}}}{{\partial t}} + {\mathit{\boldsymbol{u}}}\frac{{\partial {\mathit{\boldsymbol{v}}}}}{{\partial x}} + {\mathit{\boldsymbol{v}}}\frac{{\partial {\mathit{\boldsymbol{v}}}}}{{\partial y}} + {\mathit{\boldsymbol{w}}}\frac{{\partial {\mathit{\boldsymbol{v}}}}}{{\partial z}} = \\ - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + \gamma (\frac{{{\partial ^2}{\mathit{\boldsymbol{v}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{\mathit{\boldsymbol{v}}}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{\mathit{\boldsymbol{v}}}}}{{\partial {z^2}}}) + {F_y}\\ \frac{{\partial {\mathit{\boldsymbol{w}}}}}{{\partial t}} + {\mathit{\boldsymbol{u}}}\frac{{\partial {\mathit{\boldsymbol{w}}}}}{{\partial x}} + {\mathit{\boldsymbol{v}}}\frac{{\partial {\mathit{\boldsymbol{w}}}}}{{\partial y}} + {\mathit{\boldsymbol{w}}}\frac{{\partial {\mathit{\boldsymbol{w}}}}}{{\partial z}} = \\ - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} + \gamma (\frac{{{\partial ^2}{\mathit{\boldsymbol{w}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{\mathit{\boldsymbol{w}}}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{\mathit{\boldsymbol{w}}}}}{{\partial {z^2}}}) + {F_z} \end{array} \right. $
(3) 式中, γ表示运动粘性系数; Fx, Fy, Fz分别表示体积力F在3个坐标轴上的分量。
但是由于直接求解上述方程有一定的难度，故运用雷诺方程，采用时间平均分配的求解方式。对于不可压缩流体的标准k-ε模型，湍动能方程和湍流耗散方程分别为[14]：
$ \begin{array}{l} \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{\mathit{\boldsymbol{u}}})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}[(\mu + \frac{{{u_t}}}{{{\sigma _k}}})\frac{{\partial k}}{{\partial x}}] + \\ \;\;\;\;\;\;\;{G_1} + {G_2} - \rho \varepsilon - Y + {S_k} \end{array} $
(4) $ \begin{array}{l} \frac{{\partial (\rho \varepsilon )}}{{\partial t}} + \frac{{\partial (\rho \varepsilon {\mathit{\boldsymbol{u}}})}}{{\partial x}} = \frac{\partial }{{\partial {x}}}[(\mu + \frac{{{u_t}}}{{{\sigma _\varepsilon }}})\frac{{\partial k}}{{\partial x}}] + \\ \;\;\;\;{G_{1\varepsilon }}\frac{\varepsilon }{k}({G_1} + {C_{3\varepsilon }}{G_2}) - {C_{2\varepsilon}} \rho \frac{{{\varepsilon ^2}}}{k} + {S_\varepsilon } \end{array} $
(5) 式中, 湍流粘度ut=ρCμk/ε，k是湍动能，ε是耗散率，Cμ是湍流模型中的一个经验常数，约为0.09;G1为平均速度梯度引起的湍动能的产生项；G2为浮力引起的湍动能的产生项；Y代表不可压缩湍流中脉动的变化；C1ε, C2ε和C3ε是依据经验得到的常值；σk和σε分别为与湍动能和耗散率对应的普朗特数；Sk和Sε是源项; μ为动力粘度。
-
根据普朗特的边界层思想，在物体表面总是存在一层黏性边界层，而且对于黏性流体，在壁面上将产生涡量，并将扩散和对流到流场中去[15]。在黏性流动中，壁面是个涡量源。当流体与它流过的物体表面之间发生黏性摩擦时，流体的流速就会减慢，流速的减缓会导致流体被吸附在壁面上流动，这称作科安达效应，亦称附壁作用。
-
雷诺数是一种可用来表示流体流动情况的无量纲数，利用雷诺数可区分流体的流动是层流或湍流，也可用来确定物体在流动中流动所受到的阻力。
雷诺数方程:
$ Re = \frac{{vd}}{\lambda } = \frac{{\rho vd}}{\mu } $
(6) 式中, ρ和v分别为流体的密度和流过截面的速度；γ为运动粘性系数；d为一特征长度。水的密度、运动粘性系数和动力粘度分别为103kg/m3, 103m2/s，106Pa/s。
-
本研究是根据3种不同的水流装置来建造几何模型[16-17]，每一种模型的建立都是根据实体结构的样式来确定，运用Gambit进行网格的划分，有一个比较好的网格划分质量是仿真保证计算准确性的一个前提。
根据图 1a的结构，采用2维的结构图就可以展现出其中的流体特点，故画出如图 1b的几何模型，根据整个结构的形状，采用四边形网格更具有配合性，故而采用结构化四边形网格进行划分。
Figure 1. Geometric model and meshing of the first device
根据图 2a的结构，采用2维的结构图难以展现其中流体的特点，故建造3维结构的几何模型如图 2b所示，根据模型的结构形状，采用四面体/混合网格类型进行划分网格。
Figure 2. Geometric model and meshing of the second device
图 3的结构使得水流上方水流与空气分离，利于稳定上方水层。而且图 3的结构和图 2的结构形状很相似，故采用相似的网格划分模型，如图 3b所示，同样也采用四面体/混合网格类型进行划分网格。在设计图 2和图 3的几何模型时，为了能有个很好的对比性，设计靶材上方的水层厚度同为10cm。
Figure 3. Geometric model and meshing of the third device
-
本文中重点关注的是，对激光加工效果影响显著的靶材上方的流体流动特性。根据流体不同的结构装置形状，要选择合适的求解模型，由于图 1中的装置和图 3中的装置都是个封闭的腔体，故选择单相流模型，而图 2中的装置采用多项流混合模型。边界为速度入口和压力出口，外界压力为一个标准大气压，其余边界为无滑移边界壁面。在每个装置入口处的初始速率设置为20m/s，为了说明层流紊流状态下的流动情况，单独对装置2增加一入口速率25m/s。
-
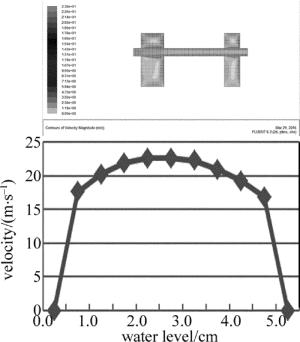
本文中的3种装置都是运用FLUENT仿真软件基于压力基求解器来模拟仿真流场，以20m/s的入口速率流入图 2和图 3的装置中，由于3维的速度云图不能显示出速度场，所以借助2维的截面速度云图来说明，如图 4所示。
Figure 4. Speed cloud picture of cross section (inlet velocity of 20m/s)
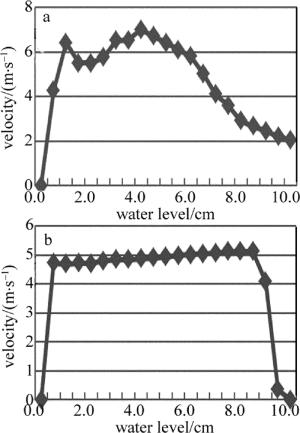
为了更好说明靶材上方流场的速度情况，选取垂直于靶材方向即是z轴正方向的水层，靶材中心处取得不同水层高度流速的位置关系图，如图 5所示。图 5a和图 5b分别对应装置2和装置3。
Figure 5. Water flow velocity and water level (inlet velocity of 20m/s)
从图 5中可以清晰地看出，流速先是快速地升高，然后流速维持在一定的范围内，而在距离上端不同约束界面的时候，图 5a中的曲线慢慢趋于平缓，图 5b中的曲线则是快速地减小为零，而且还能看出, 图 5b中的流速高度位置曲线的中间区域平滑性要比图 5a中的线性要好。根据二者结构的差异性，图 2中的装置水层上表面是空气，为柔性约束，流体上表面受到的流体阻力相对较小，使得上层流速减弱比较缓慢；而图 3中的装置水层上表面是无滑移壁面，为固体约束，流体上表面受到的流体阻力比较大，使得上层流速减低很快，紧挨着壁面的速率为0m/s。
同为无滑移壁面的装置1，同样以入口20m/s的流速流入进行模型仿真，选取垂直于靶材方向，取得不同水层高度流速的位置关系图，如图 6所示。
Figure 6. a—speed cloud picture b—water flow velocity and water level (inlet velocity of 20m/s)
从图中可以看出，装置1靶材上方的速度流场值要比装置3的速度流场值大很多，从流速与高度关系位置图中看出，线性近似为抛物线形状，在中心处有最大速度值。通过对比装置1和装置3的两者结构的差异，关键点在于水流入口的位置与方向，装置1入口位置与靶材在同一平面上，而且水流直接直接从靶材上方流过，能量损失较小；而装置3由于结构的原因，水流进入装置后先对底部进行一次冲击，而后经过靶材上方从出口流出，冲击的效果对流体的能量损失很大。
对比装置1和装置3的流速和水层高度关系位置图，分别近似为抛物线型和折线型，考虑到水为黏性流体的性质，根据科安达效应，流体受到壁面摩擦阻力的作用，使得靠近壁面的流速越来越小。其次，由于水流的入口位置和方向，以及装置结构的特定的作用。
水辅助激光加工过程中，要想获得良好的加工表面质量，熔渣的排除和切缝表面的冷却效果是非常重要的因素。熔渣依附于水流而排除，切缝的温度通过水流来降温。通过对装置2的水流场传递动量进行了更进一步的研究，探究在靶材上方流场层流、紊流状态下流速的状况。水的流动层流紊流雷诺数临界值为Re=2000, 特征长度d=13.3cm，通过(6)式计算出层流、紊流状态分界时的靶材上方流度值为15m/s，现分别以入口20m/s, 25m/s的流速进行模拟仿真，得到垂直于靶材方向的水流速度位置关系如图 7所示。
Figure 7. Relationship between flow velocity and water level
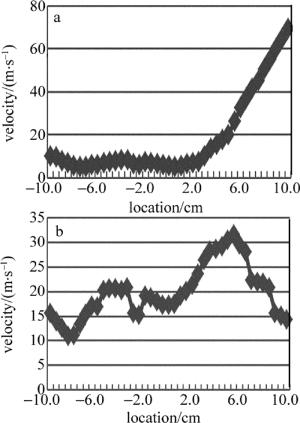
从图 7得出，速率的最大值分别为7m/s和18m/s，小于15m/s的为层流，大于15m/s的为紊流。分析层流和紊流状态下靶材上方1cm高度的流度状况，两种不同入口速度下的流速情况如图 8所示。
Figure 8. Relationship between flow velocity and location
图 8是以上两种线性在层流与紊流的状态下所仿真出来的流速位置图。图 8a中的线形先是平缓而后再升高，图 8b中则是速度波动比较大。由于层流只存在粘滞切应力，流体的质点近似做平滑的直线流动；紊流中除了粘滞切应力外，还有紊流附加切应力，这是因为N-S方程导出时均紊流运动时的雷诺应力、紊流脉动和上下层质点相互掺混，使得流体的运动呈随机性，速度随空间做不规则的脉动。靶材上方的水流具有一定的流速和平稳性，能够很好地达到熔渣有效去除和降低热影响区的效果。相比于紊流状态，层流状态下，有很大区域速度场是比较平稳的，适于放置靶材。
-
采用FLUENT仿真软件对3种不同装置的靶材上方的流场进行了模拟与分析，通过对比分析了不同装置下，同一入口速度、柔性约束和固体约束对靶材上方流场的影响，得出固体约束使得流场更具有稳定性；在不同结构装置下，对比分析了水流入口方向与位置对流场的影响，得出装置的结构特性使得能量有一定的损失，而且壁面内摩擦力使得流体的能量也具有损失；通过分析层流、紊流不同流动状态下靶材上方1cm流速状况，得出在层流状态下，靶材上方速度稳定性好，同时说明在层流状态下，适当地提高流速有利于熔渣排除和降低加工靶材的热效应。这对选择水辅助激光加工构建控制水层流动的装置提供了理论基础。
基于水辅助激光加工的水层流动特性的研究
Investigation of water flow characteristics based on water assisted laser processing
-
摘要: 为了研究水辅助激光加工靶材上方水层流动的特性，采用流体动力学分析软件FLUENT，对3种不同结构的水辅助激光加工的水流装置进行建模仿真，分析了靶材上方流体的速度场，并对结果进行对比分析。结果表明，由垂直于靶材上方的速度位置图的分析可知，装置结构的差异使得流场也具有差异性; 靶材上方1cm以内位置，流体速度平稳，有利于传输激光，排出熔渣和放置加工材料。这对选择水辅助激光加工构建控制水层流动的装置提供了理论依据。Abstract: In order to study the water flow characteristics of target layer during the water assisted laser processing, fluid dynamics analysis software FLUENT was used to do the model and simulation of three different flow devices for water assisted laser processing. The velocity field of fluid above target material was analyzed and the results were analyzed in contrast. The results show that, flow field has difference with the difference of device structure based on the analysis of speed-position curves perpendicular to target material. The fluid speed is smooth within the position of less than 1cm above target. The position is good for laser transmission, slag discharge and processing material placement. The study provides a theory basis for building water flow control device of water assisted laser processing.
-
Figure 2. Geometric model and meshing of the second device
a—geometric model b—meshing
Figure 5. Water flow velocity and water level (inlet velocity of 20m/s)
a—the second device b—the third device
Figure 6. a—speed cloud picture b—water flow velocity and water level (inlet velocity of 20m/s)
Figure 7. Relationship between flow velocity and water level
a—the maximum speed of 7m/s, inlet velocity of 20m/s b—the maximum speed of 18m/s, inlet velocity of 25m/s
-
[1] LIU J M, CAO F G. Application and development trend of laser combined machining technology[J]. Electromachining & Mould, 2006, 4(5):5-9 (in Chinese). [2] CHEN Y L, XU B C, YUAN G F, et al. Study on the removed quantity of difficult to machine materials in laser chemical combined[J]. China Mechanical Engineering, 2009, 20(11): 1356-1360 (in Chinese). [3] ZHANG H, XU J W, WANG J M. Experimental study of neutral salt solution assisted laser machining[J]. Chinese Journal of Lasers, 2008, 35(11):1836-1840 (in Chinese). doi: 10.3788/JCL [4] SU H X. Water guided laser processing technology[J]. Optoelectronic Technology & Information, 1998, 11(3):35-38 (in Chinese). [5] WANG X Y, XU W X, XU W J, et al. Simulation and experiment of laser bending of silicon sheet[J]. Optics and Precision Engineering, 2008, 16(4): 605-610(in Chinese). [6] ZHAN C J, LI C F, PAN Y C, et al. Analysis of fluid flow in micro-waterjet guided laser precision drilling process[J]. Chinese Quarterly of Mechanics, 2011, 32(2): 159-165 (in Chinese). [7] ZHANG C T, YUAN G F, CHEN X H, et al. Experimental study about effect of water-jet to laser etching of crystal silicon[J]. Applied Laser, 2014, 31(6): 557-561 (in Chinese). [8] FU Y H, CAO J, DONG F, et al. CFD simulation of the laser stable water beam in micro water-jet guided laser[J]. Fluid Machinery, 2013, 42(8): 21-25 (in Chinese). [9] EDDIE Y K.The stability of 30μm-diameter water jet for jet-guided laser machining[J].International Journal of Advanced Manufacturing Technology, 2015, 7(8):939-946. [10] ZHOU J J, XU G Q, ZHANG H J. FLUENT software engineering techniques and case analysis[M]. Beijing: China Water & Power Press, 2010:39-365(in Chinese). [11] DING X S, JIAO N. Fluent 14.5 fluid simulation calculation from the Introduction to the master[M]. Beijing: Tsinghua University Press, 2014:23-186(in Chinese). [12] LI J, ZHANG Q, ZHOU Y Zh.Analysis of influence of nozzle convergence on water-jet capacity[J]. Information Technology, 2015, 44(5): 102-104 (in Chinese). [13] YANG Y S, ZHANG J P, NIE S L. Energy loss of nozzles in water jet system[J]. Journal of Mechanical Engineering, 2013, 49(2):139-144(in Chinese). doi: 10.3901/JME.2013.02.139 [14] PEI E R, CHAI J Ch. Research on the flow characteristic of spray nozzle and design[J]. Journal of Drainage and Irrigation Machinery Engineering, 2004, 22(5): 29-31(in Chinese). [15] ZHUANG L X, YIN X Y, MA H Y. Fluid mechanics[M]. Hefei: University of Science and Technology of China Prass, 2009:145-336 (in Chinese). [16] WISAN C, VIBOON T, CHAIYA D. Preliminary study of ultrasonic assisted underwater laser micromachining of silicon[J]. Applied Mechanics and Material, 2016, 835(2):139-143. [17] WEE L M, KHOONG L E, TAN C W, et al. Solvent-assisted laser drilling of silicon carbide[J]. International Journal of Applied Ceramic Technology, 2011, 8(6): 1263-1276. doi: 10.1111/ijac.2011.8.issue-6 -
点击查看大图
图(8)
计量
- 文章访问数: 5209
- HTML全文浏览量: 3154
- PDF下载量: 18
- 被引次数: 0
