网站地图
下载:
-
扭曲向列型液晶(twist nematic liquid crystal，TN-LC)中，液晶分子长轴在上下两个电极表面之间旋转了90°，偏振光从上电极表面传播到下电极表面时，偏振方向会旋转90°，因此具有旋光特性，如图 1所示。当给液晶板施加一定大小的交流电压后，液晶将会发生Fredericks转变[8]，当电压增大到某一值(称为阈值电压)起，除电极附近的分子外，液晶分子的长轴开始向电场方向倾斜，导致其旋光性消失，光学特性也随之发生变化，这就是液晶的电光效应。
Figure 1. Working principle of liquid crystal optical switching
液晶未加电压时呈亮态，加电压后呈暗态的显示模式称为“常白”(normally white，NW)模式。对于“NW”模式的TN-LC，其电光特性曲线如图 2所示。
Figure 2. Electro-optic characteristic curve of TN-LC
图 2中，V10和V90分别代表透射光强度达到最大透射光强的10%及90%时的外加电压值，根据连续体理论[9]，TN-LC的临界电压值为：
$ {V_{{\rm{th}}}} = {\rm{ \mathsf{ π} }}\sqrt {\frac{{{K_{11}} + \left( {{K_{33}} - 2{K_{22}}} \right)/4}}{{\Delta \varepsilon }}} $
(1) 式中，K11, K22和K33分别为液晶的展曲系数、扭曲系数和弯曲系数，Δε为液晶介电常数各向异性的大小，数值上等于平行与垂直于液晶长轴的介电常数之差。
-
液晶的光学性质一般采用Jones矩阵进行分析，首先将液晶层分割成许多小薄片，每个小薄片相当于一个线偏振器。图 3为扭曲向列液晶的几何排列。
Figure 3. Geometric arrangement of TN-LC
此时入射光的Jones矩阵为[8]:
$ {\mathit{\boldsymbol{E}}_{\rm{i}}} = \left[ \begin{array}{l} \cos \theta \\ \sin \theta \end{array} \right] $
(2) 式中, θ是上偏振片P1与上基板液晶指向矢n1的夹角。
出射光的Jones矩阵为：
$ \begin{array}{l} {\mathit{\boldsymbol{E}}_{\rm{o}}} = \left[ {\begin{array}{*{20}{c}} {\cos \gamma }&{\sin \gamma } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos \phi }&{ - \sin \phi }\\ {\sin \phi }&{ - \cos \phi } \end{array}} \right] \cdot \\ \left[ {\begin{array}{*{20}{c}} {\cos X - {\rm{i}}\frac{\mathit{\Gamma }}{{2X}}\sin X}&{\frac{\phi }{X}\sin X}\\ { - \frac{\phi }{X}\sin X}&{\cos X - {\rm{i}}\frac{\mathit{\Gamma }}{{2X}}\sin X} \end{array}} \right]\left[ \begin{array}{l} \cos \theta \\ \sin \theta \end{array} \right] \end{array} $
(3) 式中，γ是下偏振片P2与上基板液晶指向矢n1的夹角，$\mathit{\Gamma } = \frac{{2{\rm{ \mathit{ π} }}\Delta nd}}{\lambda }, X = \sqrt {{\phi ^2} + {{\left( {\gamma /2} \right)}^2}}$, ϕ是上基板液晶指向矢为参考矢的液晶的扭曲角，d为液晶的厚度，Δn=ne-no为液晶的双折射，λ为入射光波长。
当入射电压为零时，可得工作在导波方式的扭曲向列液晶的透过率为[8]：
$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;T = \\ {\left[ {\cos \beta \cos \left( {\phi + \theta - \gamma } \right) + \frac{{\sin \beta }}{{\sqrt {1 + {\alpha ^2}} }}\sin \left( {\phi + \theta - \gamma } \right)} \right]^2} + \\ \;\;\;\;\;\;\;\frac{{{\alpha ^2}}}{{1 + {\alpha ^2}}}{\sin ^2}\beta {\cos ^2}\left( {\phi + \theta - \gamma } \right) \end{array} $
(4) 式中，$\alpha = \frac{{\Delta nd}}{{\phi \lambda }}{\rm{ \mathsf{ π} }}, \beta = \phi \sqrt {1 + {\alpha ^2}} $, 本实验中所用为常白型扭曲向列液晶屏(liquid crystal display, LCD)，即P1⊥P2，且$\phi = \frac{{\rm{ \mathsf{ π} }}}{2}$，则θ=0，$\gamma = \frac{{\rm{ \mathsf{ π} }}}{2}$，因此有:
$ T = 1 - \frac{{{{\sin }^2}\beta }}{{1 + {\alpha ^2}}} $
(5) 当$\alpha = \sqrt 2 , \sqrt {15} , \sqrt {35} , \cdots , \sqrt {4{N^2} - 1} , \cdots , \left( {N = 1, 2, 3, \cdots } \right)$时，液晶的透过率最大。以本实验中波长为635nm的入射光源为例，其前3个亮态对应的Δnd的值分别为：0.55μm, 1.23μm和1.88μm，其透过率T随α值的变化如图 4所示。
Figure 4. Relationship between T and α
由此可知，对于不同波长的入射光，其透过率达到最大值时所对应的液晶厚度是不同的。在第一极大值附近，液晶厚度的微小波动就会引起透过率的较大变化，随着厚度的增加，其对液晶透过率的影响逐渐减弱。在实际应用中，液晶屏厚度的增加会降低其性能，因此有实力的生产厂家均努力降低液晶屏的厚度。
-
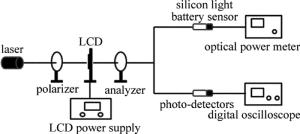
本实验装置由半导体激光器(450nm, 532nm, 635nm)、导轨、滑块、起偏器、液晶屏、检偏器、光功率计(传感器为硅光电池)、光电探头及数字示波器等组成，如图 5所示。
Figure 5. Schematic diagram of liquid crystal experimental device
-
测量液晶的电光特性曲线时，首先将检偏器和起偏器设成垂直模式，使零电场条件下透过LCD的光强达到最大值，然后通过改变LCD上的外加电压(2.5V~12V)来考察液晶光开关的性质，利用功率计测量该电压下LCD的透光强度，从而得出相应的电光特性曲线。实验过程中各光学元件的相对位置保持不变，实验数据如图 6所示。
Figure 6. Electro-optic characteristic curve of TN-LCD
从图 6可以看出，3种光源下液晶的透光强度随驱动电压均有先降后升的趋势。当驱动电压在2.5V~4.5V范围时，液晶的透光强度变化不明显；继续增大驱动电压至5V左右时，透光强度出现强烈的衰减，原因是在该驱动电压范围内，液晶光栅开始出现衍射现象，光功率被分布到了每一个衍射光斑上，此时中心光斑强度较弱，如图 7所示。当继续增大驱动电压时，衍射光斑慢慢消失，中心光斑的强度逐渐增大，因而透光强度出现先降后升的趋势。
Figure 7. Diffraction spots of TN-LCD(voltage:5V)
由(1)式可知，液晶的阈值电压不受入射光波长的影响，实验中各光源下液晶透光强度的锐减均出现在4.8V，说明实验结果符合理论分析。对于单色光而言，透光强度对所加电压很敏感，稍微改变驱动电压，透过率就会发生变化，这与液晶的电控双折射效应有关[10-11]。
-
根据连续弹性体理论，液晶的响应时间与液晶的弛豫特性有关。液晶弛豫包括介电极化弛豫和转向弛豫，由于液晶的介电性，当施加电压时，介电体的极化需要时间，因此电场并非立即加在液晶上。而由电场引起的液晶分子的变化同样需要时间，反映在时间响应曲线上，用上升时间和下降时间描述，其表达式为[8]：
$ {\tau _{{\rm{on}}}} = \frac{{\eta {d^2}}}{{\Delta \varepsilon {V^2} - {{\rm{ \mathsf{ π} }}^2}k}} $
(6) $ {\tau _{{\rm{off}}}} = \frac{{\eta {d^2}}}{{{{\rm{ \mathsf{ π} }}^2}k}} $
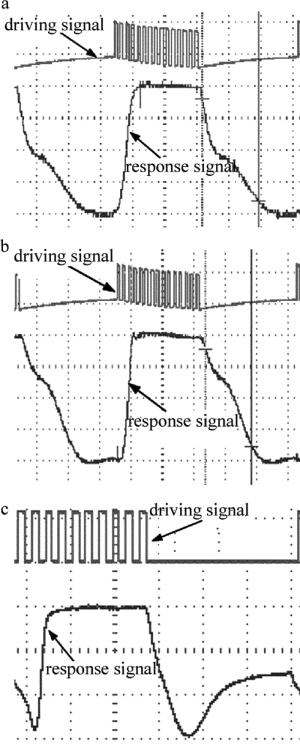
(7) 式中，η是黏度，k为弹性系数，V为外加电压。从公式中可以看出，液晶的厚度和液晶样品的黏度是影响液晶响应时间的重要因素。由于液晶对不同波长光源的扭曲角不同，其时间响应曲线也有差异，图 8为不同波长下的液晶响应时间。
Figure 8. Response signals of liquid crystal under different light source
-
由于空间电荷场和外加电场对液晶分子的力矩作用使向列相液晶分子的指向矢重新取向，产生了光致折射率改变，从而形成光栅。当两束相干线偏振光束I1和I2在液晶中相遇，则在液晶层内形成周期性的干涉光强分布[12]：
$ I\left( \mathit{\boldsymbol{r}} \right) = {I_0}\left[ {1 + m\cos \left( {\mathit{\boldsymbol{q}} \cdot \mathit{\boldsymbol{r}}} \right)} \right] $
(8) 式中, I0=I1+I2为总光强，$m = \frac{{2\sqrt {{I_1}{I_2}} }}{{{I_0}}}$是光强调制度，$\left| \mathit{\boldsymbol{q}} \right| = \frac{{2{\rm{ \mathit{ π} }}}}{\mathit{\Lambda }}$为光栅波矢，Λ为光栅常数，r为位置矢量。则液晶层中形成的折射率光栅为[13]:
$ \Delta {n_{\rm{g}}} = \Delta {n_{\rm{e}}}\cos \left( {qx + {\phi _{{\rm{SC}}}}} \right){E_{{\rm{DC}}}}{E_{{\rm{SC}}}} $
(9) 式中，$\Delta {n_{\rm{e}}}{\rm{ = }}\left( {{n_{//}} - {n_ \bot }} \right)\frac{{{n_{//}}}}{{{n_ \bot }}}\left( {\sin 2\beta } \right){\theta _0}$，EDC为外加直流电场，ESC为空间电荷场，ϕSC为折射率光栅相对于强度干涉条纹的空间相移，θ0为液晶分子的取向角，n⊥和n//分别为光电场垂直和平行指向矢时的折射率，x代表空间电荷场方向的位置。
当驱动电源达到一定的电压值时，激光通过液晶屏后会产生衍射现象，如图 9a所示。当驱动电压小于5V时，出现由圆形衍射环和水平衍射光斑组成的衍射图像，此时圆环状衍射图样比较清晰，且各级衍射光斑都位于圆环状衍射图样相应的环带上。随着电压的增大，圆环逐渐消失，水平光斑亮度逐渐增大，如图 9b所示。
Figure 9. Diffraction patterns of red incident source at 635nm
图 10为蓝色激光光源下液晶衍射光斑及其光强分布图。图中以中心光斑位置为原点，考查了各级衍射光斑与中心光斑的间距x(横轴)及相对光强$\frac{I}{{{I_0}}}$(纵轴)的变化情况。从图中可以看出, 液晶光栅的衍射光斑并非绝对的规则和对称，主要原因是正性液晶的电流体不稳定性造成的[9]。随着入射光源波长的增大(蓝光＜绿光＜红光)，各级衍射光斑的间距逐渐增大，即衍射角随着入射波长的增大而增大，且光斑的强度分布变化明显。以蓝色激光光源(450nm)为例，其第4级衍射光斑的强度也较强，且能观察到明显的中心亮斑；相比之下，红色光源的衍射图像中只有1级和2级的衍射光斑较亮。由于液晶衍射光栅驱动电压低、功耗小、重量轻等优点，可用于空间光通信中对激光源进行方位探测和自动跟瞄[14]。
Figure 10. Diffraction patterns of blue incident source at 6V driving voltage
-
对扭曲向列液晶的电光特性进行了理论分析和实验研究。实验结果符合理论分析，即液晶的光开关特性与液晶本身及驱动电压有关，与入射光源无依赖关系；液晶对不同波长入射光的扭曲角不同，导致不同入射光源下液晶的响应时间有一定的差异。对液晶光栅的理论分析及实验研究表明，波长及电场对各级衍射光斑的空间及能量分布均会产生影响。以上研究对液晶器件的开发利用具有一定的借鉴意义。
基于激光光源的液晶特性研究
Study on property of liquid crystal based on laser source
-
摘要: 为了研究激光光源对液晶电光特性的影响, 采用Jones矩阵对液晶的光学特性进行了分析, 同时利用不同波长的半导体激光器作为入射光源, 对液晶的电光特性进行了实验研究。结果表明, 当电压达到4.8V时, 各光源下液晶的透光强度均出现陡降, 说明液晶的阈值电压与入射光波长无依赖关系; 通过示波器跟踪图像发现各光源下液晶的响应时间有明显的差异; 随着供电电压的增大, 液晶光栅的衍射光斑由圆环状逐渐转为平行分布, 且各级衍射光斑并非完全对称, 入射波长及供电电压决定了衍射光斑的空间及能量分布。该研究结果对液晶器件的研发具有一定的借鉴意义。Abstract: In order to study influence of incident light on electro-optic characteristics of liquid crystal, the optical properties of liquid crystal were analyzed theoretically based on Jones matrix. By using semiconductor laser with different wavelengths as incident light, electro optical characteristics of liquid crystal were studied experimentally. The results show that the transmission intensity of the liquid crystal sample descends steeply at 4.8V and the threshold voltage of liquid crystal is independent on the wavelength of light source. The oscillograph images show that the incident light affects the response time obviously. The diffraction facula of liquid crystal sample arranges in a ring first and gradually in a line with the increase of voltage. At the same time, diffraction spot is not completely symmetrical. The spatial and energy distributions of the diffraction spot are determined by incident wavelength and power supply voltage. The study is meaningful for the research and development of liquid crystal devices.
-
Figure 8. Response signals of liquid crystal under different light source
a—response signal of 635nm laser b—response signal of 532nm laser c—response signal of 450nm laser
-
[1] HUANG D X, LIU X F. Semiconductor lasers and their applications[M].Beijing:National Defense Industry Press, 1999:67-90(in Chinese). [2] AN B, CHEN H X, CHEN Zh P. Real-time edge enhancement of optical image with liquid crystal TV [J]. Laser Technology, 2002, 26 (1): 44-46(in Chinese). [3] XI Q K, ZHU R H, CHEN L, et al.Scanning method for scanning microscope with a liquid crystal display [J]. Laser Technology, 2005, 29(5): 558-560(in Chinese). [4] LV X, JIA E B, ZHANG S L, et al. Development of liquid crystal optical switch for experiment demonstration [J]. Experimental Technology and Management, 2007, 24(12):61-63(in Chinese). [5] PALFFY-MUHOAY P, CAO W Y, MOREIRA M, et al. Photonics and lasing in liquid crystal materials [J].Philosophical Transactions of the Royal Society, 2006, 364(1847):2747-2761. doi: 10.1098/rsta.2006.1851 [6] ZHANG L L, SUN X D, LIU Y J, et al. Cholesteric liquid crystals laser with external cavity [J]. Chinese Journal of Liquid Crystals and Displays, 2013, 28(5):680-682(in Chinese). [7] CHEN J Q, LI Zh, ZHANG Y P. Automatic laser detection and protection device based on LCD light switch [J]. Laser Technology, 2013, 37(6): 777-780(in Chinese). [8] HUANG Z Q. Principle of liquid crystal display[M]. 2nd ed. Beijing: National Defense Industry Press, 2008: 142-143(in Chinese). [9] WANG X J. Liquid crystal optics and liquid crystal display [M]. Beijing: Science Press, 2006:230-263(in Chinese). [10] REN G J, ZHAO J L, YAO J Q. Study on birefringence effect of liquid crystal in communication [J]. Laser Technology, 2011, 35(2): 242-244(in Chinese). [11] PENG D Y, SONG L K, LI K T, et al. Measurement of birefringence of liquid crystal with polarized lightinterference method [J].Laser Technology, 2014, 38(3): 422-424(in Chinese). [12] REN C Y, SUN X D, SUN F, et al. Self-phase modulation in nematic liquid crystal(5CB)[J]. Chinese Journal of Liquid Crystals and Displays, 2006, 21(2): 95-98(in Chinese). [13] KHOO I C. Orientational photorefractive effects in nematic liquid crystal films[J]. IEEE Journal of Quantum Electronics, 1996, 32(3): 525- 534. doi: 10.1109/3.485406 [14] WANG L, ZHANG C, YAO Z S, et al. Simulation of liquid crystal diffraction grating[J].Chinese Journal of Liquid Crystals and Displays, 2006, 21(2): 113-117 (in Chinese). -
点击查看大图
图(10)
计量
- 文章访问数: 4660
- HTML全文浏览量: 2785
- PDF下载量: 17
- 被引次数: 0
