网站地图
-
空间碎片是指由于人类太空活动而遗留在空间中的航天器残骸及其碰撞或爆炸产生的碎片[1]，主要分布于距地面400km~2000km的近地轨道(low-earth orbit, LEO)。小尺度空间碎片易对LEO轨道内的飞行器产生威胁，且难以被跟踪探测，造成了LEO区域飞行器工作的安全隐患。为了最大程度地保障近地空间环境安全，移除LEO区域小尺度空间碎片成为了亟待研究的关键技术[2]。国内外对于空间碎片主动移除方案主要包括绳系拖拽法、捕获法和激光辐照法3类。激光辐照主动移除空间碎片技术可同时实现对小尺度空间碎片的探测和跟瞄，具有操作易、时间短、重复利用、成本较低等优势，是移除小尺度空间碎片最具前景的方法，也是当前的研究重点[3]。
近年来，国际上开展了激光清除空间碎片的研究计划，如美国的猎户座计划[4]、欧盟的太空清除计划[5]等，国内也开展了地基激光辐照小尺度空间碎片的相关研究[6-8]。参考文献[9]中对地基激光辐照空间碎片产生的烧蚀反喷作用力改变其飞行轨迹避免与卫星碰撞发生的可行性与方法进行了讨论。参考文献[10]中针对地基激光清除椭圆轨道空间碎片问题，提出了单脉冲变轨和多脉冲变轨两种计算分析方法。参考文献[11]中研究了近地轨道小尺度空间碎片移除过程中轨道偏心率与近地点高度随激光脉冲数目变化的影响规律。这些研究绝大部分考虑的是绕地球平动的空间碎片，对于碎片自旋情况的分析涉及较少。在轨空间碎片绝大部分是不规则的形状，当不规则的靶材与激光烧蚀作用时极有可能在靶材的质心产生一个扭矩，从而引起靶材的自旋。统计研究表明，LEO区域中存在一部分空间碎片在绕地球平动的同时其本身在自旋[12]。在考虑靶材的自旋时，激光与靶材的相互作用会随时间不断变化，不同时刻将对应不同的冲量，靶材获得的速度增量也将随之变化，从而对空间碎片的降轨效果产生较大影响。因此有必要就空间碎片自旋对其降轨效果的影响规律进行研究分析。
本文中以LEO区域中常见的铝合金平板为例，建立了空间碎片自旋与非自旋模型，研究了高能脉冲激光与靶材作用下碎片速度的变化规律，在此基础上建立了激光辐照作用下空间碎片的变轨模型，通过仿真分析，对高能脉冲激光作用下空间碎片轨道参量的变化规律进行了数值模拟，为地基激光清除空间碎片技术的应用可提供必要的理论基础。
-
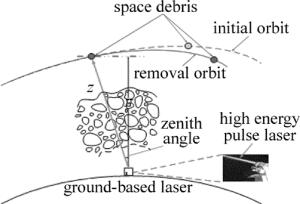
地基激光清除空间碎片的方法描述如下：地基激光器发射高能脉冲激光束，经过大气层并进入自由空间传输，空间碎片靶面被强脉冲激光辐照后，根据其所具备的条件不同而发生升温、熔融、气化、等离子体等一系列复杂变化，碎片会产生反冲冲量，使空间碎片获得一定的速度增量，反冲冲量越大，其速度增量越大，引发空间碎片的减速和变轨，并最终坠入大气层烧毁，完成碎片清除，其示意图如图 1所示。
Figure 1. Schematic of removal of orbiting space debris by using ground-based laser
目标靶与激光的冲量耦合系数Cm表示单位入射激光的能量所获得的靶冲量，可联系激光能量与靶冲量两个参量，是衡量激光清除空间碎片能力的重要参数指标，表达式为[13]：
$ {C_m} = \frac{{m\Delta v}}{E} = \frac{p}{I} $
(1) 式中，m表示靶材的质量，Δv表示靶材的速度增量，E表示单脉冲激光能量，I表示入射激光功率密度，p表示靶材表面的烧蚀压力，mΔv表示脉冲激光辐照作用下靶材获得的冲量。
由(1)式可得高能脉冲激光辐照作用下空间碎片获得的冲量为：
$ m\Delta v = {C_m}E $
(2) 将(2)式改写为动力学等式，其表达式为[14]:
$ m\frac{{{\rm{d}}\mathit{\boldsymbol{v}}}}{{{\rm{d}}t}} = - {C_m}\frac{{{\rm{d}}E}}{{{\rm{d}}t}}\mathit{\boldsymbol{n}} = {C_m}I\mathit{\boldsymbol{k}} \cdot \mathit{\boldsymbol{H}} $
(3) 式中，n表示空间碎片的曲面法向量，k表示高能脉冲激光的辐照方向，H表示碎片的二阶面积矩阵，其表达式为:
$ \mathit{\boldsymbol{H}} = \sum\limits_\alpha {{A_\alpha }{\mathit{\boldsymbol{n}}_\alpha }{\mathit{\boldsymbol{n}}_\alpha }} \to \int {{\rm{d}}A\mathit{\boldsymbol{nn}}} $
(4) 式中, A表示铝板平面的面积, α表示不同的曲面, Aα和nα表示不同曲面的面积和曲面法向量。
空间碎片呈现多种形状，本文中选取LEO区域中常见的铝板为例进行理论分析。铝板是能够体现激光辐照作用下烧蚀反冲现象最简单的例子，不论激光入射方向如何，烧蚀反冲方向始终沿着烧蚀平面的曲面法线。
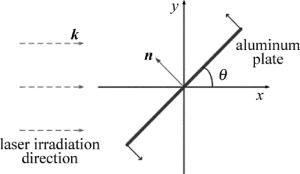
现就铝板模型作如下假设：(1)假定碎片在单脉冲高能激光烧蚀作用下的速度增量是瞬时获得的，仅考虑脉冲间隔内碎片的轨道变化；(2)假定高能脉冲激光从左边辐照铝板，辐照方向为k，以铝板的质点为原点，以x =k为x轴，过原点垂直于x轴为y轴，建立一个平面直角坐标系，θ为铝板与x轴的夹角，如图 2所示；(3)假定激光对铝板的烧蚀只作用在x-y平面内，不考虑z轴的影响，忽略铝板的边缘；(4)假定铝板平面足够平坦且较薄。该模型对靶材平面的形状没有具体要求，具有一定的适用性。本文中针对铝板自旋与否分别建立两种靶材模型。
Figure 2. Schematic of a thin aluminum plate projected onto the x-y-plane
首先分析不考虑铝板自旋的靶材模型，铝板平面的法向量可表示为:
$ \mathit{\boldsymbol{n}} = \left[ {\begin{array}{*{20}{c}} { - \sin \theta }\\ {\cos \theta } \end{array}} \right] $
(5) 由于假定的铝板模型不考虑z轴的影响，所以(5)式中铝板法向量忽略了z轴分量。由(5)式可得铝板的二阶面积矩阵(同样不考虑z轴分量)和激光烧蚀作用下的加速度分别为:
$ \mathit{\boldsymbol{H}} = A\left[ {\begin{array}{*{20}{c}} {{{\sin }^2}\theta }&{ - \sin \theta \cos \theta }\\ { - \sin \theta \cos \theta }&{{{\sin }^2}\theta } \end{array}} \right] $
(6) $ \frac{{{\rm{d}}\mathit{\boldsymbol{v}}}}{{{\rm{d}}t}} = - \frac{{{C_m}IA}}{m}\sin \theta \mathit{\boldsymbol{n}} $
(7) 对(7)式进行积分，可得激光与靶材烧蚀作用下，铝板在x轴和y轴获得的速度增量分别为:
$ \left\{ \begin{array}{l} \Delta {v_x} = \frac{{{C_m}IA}}{m}t{\sin ^2}\theta \\ \Delta {v_y} = - \frac{{{C_m}IA}}{m}t\sin \theta \cos \theta \end{array} \right. $
(8) 式中，t表示时间。
下面分析考虑铝板自旋的靶材模型，假定铝板绕其质点沿逆时针方向自旋，设其角速度为常数ω(ω=ωn)且不受激光烧蚀作用的影响，则铝板平面的法向量可表示为:
$ \mathit{\boldsymbol{n}} = \left[ {\begin{array}{*{20}{c}} { - \sin \left( {\omega t + \theta } \right)}\\ {\cos \left( {\omega t + \theta } \right)} \end{array}} \right] $
(9) 由(9)式可得自旋铝板的二阶面积矩阵和激光烧蚀作用下的加速度分别为:
$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{H}} = A \times }\\ {\left[ {\begin{array}{*{20}{c}} {{{\sin }^2}\left( {\omega t + \theta } \right)}&{ - \sin \left( {\omega t + \theta } \right)\cos \left( {\omega t + \theta } \right)}\\ { - \sin \left( {\omega t + \theta } \right)\cos \left( {\omega t + \theta } \right)}&{{{\sin }^2}\left( {\omega t + \theta } \right)} \end{array}} \right]} \end{array} $
(10) $ \frac{{{\rm{d}}\mathit{\boldsymbol{v}}}}{{{\rm{d}}t}} = - \frac{{{C_m}IA}}{m}\sin \left( {\omega t + \theta } \right)\mathit{\boldsymbol{n}} $
(11) 对(11)式进行积分，可得激光与靶材烧蚀作用下，自旋铝板在x轴和y轴获得的速度增量分别为:
$ \left\{ \begin{array}{l} \Delta {v_x} = \frac{{{C_m}IA}}{{2m\omega }}\left[ {\omega t - \sin \left( {\omega t} \right)\cos \left( {\omega t + 2\theta } \right)} \right]\\ \Delta {v_y} = - \frac{{{C_m}IA}}{{2m\omega }}\sin \left( {\omega t} \right)\sin \left( {\omega t + 2\theta } \right) \end{array} \right. $
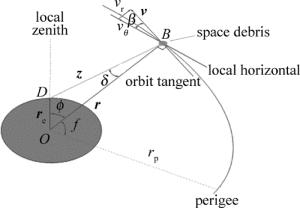
(12) 下面建立高能脉冲激光辐照作用下空间碎片的动力学变轨仿真模型。碎片轨道参量的几何变量的关系示意图如图 3所示。其中D表示地基激光器的位置，B表示空间碎片的位置，z表示高能脉冲激光的辐照方向，β表示当地的轨道倾角，ϕ表示空间碎片与当地天顶的夹角，δ表示高能脉冲激光辐照空间碎片的辐照方向与碎片运动轨道平面内的轨道半径的夹角，则:
Figure 3. Geometry of laser-target interaction
$ \beta = \arctan \left( {{v_{\rm{r}}}/{v_\theta }} \right) $
(13) $ \delta = - \arcsin \left[ {\left( {{r_{\rm{e}}}\sin \phi } \right)/z} \right] $
(14) 式中，vθ和vr分别是碎片的周向和径向初始速度分量，re表示地球半径，z表示地基激光器和空间碎片的距离，可表示为:
$ {z^2} = {r^2} + r_{\rm{e}}^2 - 2r{r_{\rm{e}}}\cos \phi $
(15) 式中，r表示碎片运动轨道平面内的轨道半径，可表示为:
$ r\left( \phi \right) = \frac{{{r_{\rm{p}}}\left( {1 + e} \right)}}{{1 + e\cos \left( {\phi + {\phi _0}} \right)}} $
(16) 式中，ϕ0表示近地点相对当地天顶的角度。
碎片的初始真近角为:
$ f = \phi + {\phi _0} $
(17) 轨道的偏心率为:
$ e = \frac{{{r_{\rm{a}}} - {r_{\rm{p}}}}}{{{r_{\rm{a}}} + {r_{\rm{p}}}}} $
(18) 式中，ra和rp分别表示轨道的远地点和近地点高度。
轨道的半长轴为:
$ a = \frac{{{r_{\rm{p}}}}}{{1 - e}} $
(19) 半通径为:
$ q = a\left( {1 - {e^2}} \right) $
(20) 碎片的周向和径向初始速度分量分别为:
$ \left\{ \begin{array}{l} {v_\theta } = \sqrt {\frac{{MG}}{q}} \left[ {1 + e\cos \left( {\phi + {\phi _0}} \right)} \right]\\ {v_{\rm{r}}} = \sqrt {\frac{{MG}}{q}} \left[ {e\cos \left( {\phi + {\phi _0}} \right)} \right] \end{array} \right. $
(21) 式中，M表示地球质量，G表示万有引力常数。
碎片总的速度为:
$ {v^2} = v_{\rm{r}}^2 + v_\theta ^2 = MG\left( {\frac{2}{r} + \frac{1}{a}} \right) $
(22) 高能脉冲激光辐照空间碎片产生反冲冲量，在反冲冲量作用下，碎片获得一个速度增量，改变其原有运行轨道，碎片的轨道参量也随之发生改变。碎片周向和径向的速度增量分别为:
$ \left\{ \begin{array}{l} \Delta {v_\theta } = - \Delta {J_\theta } = \Delta {v_x}\sin \xi - \Delta {v_y}\cos \xi \\ \Delta {v_{\rm{r}}} = - \Delta {J_{\rm{r}}} = \Delta {v_x}\cos \xi + \Delta {v_y}\sin \xi \end{array} \right. $
(23) 式中, ξ=β-δ。
变轨后，半通径的增量为:
$ \begin{array}{*{20}{c}} {\Delta q = \frac{{2r}}{v}\left\{ {\Delta {J_\theta }\left[ {1 + e\cos \left( {\phi + {\phi _0}} \right)} \right] + } \right.}\\ {\left. {\Delta {J_{\rm{r}}}e\sin \left( {\phi + {\phi _0}} \right)} \right\}} \end{array} $
(24) 式中，ΔJθ和ΔJr分别表示ΔJ的周向和径向分量。通常的观点认为，周向分量ΔJθ是碎片的变轨的决定因素，从这个公式中可以看出，径向分量ΔJr也对碎片的变轨有较大的影响。当近地点在当地天顶下(即ϕ+ϕ0=0)时，ΔJr对碎片变轨没有作用。碎片轨道高度的变化量为:
$ \Delta H = {v_{\rm{r}}}\Delta {v_{\rm{r}}} + {v_\theta }\Delta {v_\theta } $
(25) 碎片运行至近地点时，径向速度分量vr=0，从(25)式可以看出，即使径向速度增量Δvr再大，也不会对碎片降轨产生影响。激光烧蚀对碎片的推进作用效果是瞬时改变碎片的速度，从而改变碎片的运行轨道高度，最终坠入大气层烧毁，达到清除的目的。地基激光清除空间碎片的过程中，碎片轨道的近地点(或远地点)绝大部分情况下并不会直接过顶，近地点(或远地点)的高度变化是激光与靶材相互作用的结果。
变轨后半通径的增量还可以表示为:
$ \Delta q = \left( {1 - {e^2}} \right)\Delta a - 2ae\Delta e $
(26) 由(27)式可以推导出变轨后偏心率的增量为:
$ \Delta e = \frac{{\left( {1 - {e^2}} \right)\Delta a - \Delta q}}{{2ae}} $
(27) 式中，Δa表示变轨后半长轴的增量，其表达式为:
$ \Delta a = \frac{{GM}}{{2{H^2}}}\Delta H $
(28) 初始真近角在0°~360°的范围内变化，轨道近地点、远地点高度增量分别为:
$ \left\{ \begin{array}{l} \Delta {r_{\rm{p}}} = \left( {1 - e} \right)\Delta a - a\Delta e\\ \Delta {r_{\rm{a}}} = \left( {1 + e} \right)\Delta a + a\Delta e \end{array} \right. $
(29) -
铝合金材料是LEO区域空间碎片的主要成分之一。参考文献[12]中给出的关于激光器和空间碎片的相关参量，如表 1、表 2所示。以近地点、远地点高度分别为500km, 1073km的铝合金平板为例，分别建立了地基激光清除自旋空间碎片和非自旋空间碎片的动力学变轨模型。假定铝板与x轴的夹角θ=30°，地基激光站位于初始真近角f=120°的位置，为达到碎片降速变轨的目的，要求v ·z < 0，通过数值计算即可得高能脉冲激光在f为45°~225°内的辐照空间碎片。
Table 1. Laser parameters
parameter value range 1000km laser wavelength 1.06μm beam quality factor 2.0 efficiency factor 30% mirror diameter 13m laser spot radius 31cm laser pulse energy 7.3kJ fluence on target 53kJ/m2 laser repetition rate 11.2Hz Table 2. Physical parameters of space debris
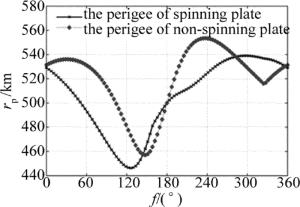
space debris description Al/plate areal mass density 10kg/m2 mass 0.75kg angular velocity 2.5rad/s impulse coupling coefficient 75μN·s/J 通过仿真得到高能脉冲激光烧蚀空间碎片的作用下考虑铝板自旋和不考虑铝板自旋的近地点高度随初始真近角的变化曲线，如图 4所示。由图 4可以看出，自旋碎片在初始真近角f=45°~126°附近与高能脉冲激光作用时，变轨后近地点高度始终减小；在初始真近角f=126°~225°附近作用时，近地点高度持续增大。非自旋碎片在初始真近角f=45°~147°附近与高能脉冲激光作用时，变轨后近地点高度始终减小；在初始真近角f=147°~225°附近作用时，近地点高度持续增大。自旋与非自旋碎片均存在高能脉冲激光最佳作用区域，即碎片降轨效果最佳区域。自旋碎片在初始真近角f=86°~151°附近降轨效果最佳，而非自旋碎片在初始真近角f=130°~162°附近降轨效果最佳。相同条件下，自旋碎片的降轨效果优于非自旋碎片，且自旋碎片的最佳作用区域更宽。
Figure 4. Perigee altitude vs. initial true anomaly
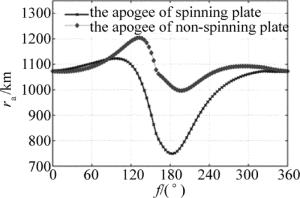
图 5中给出了自旋碎片与非自旋碎片变轨后的远地点高度随初始真近角的变化曲线。变轨后自旋碎片在初始真近角f=45°~99°或f=186°~225°附近远地点高度持续增大，在初始真近角f=99°~186°附近远地点高度始终减小；非自旋碎片在初始真近角f=45°~ 135°或f=198°~225°附近远地点高度持续增大，在初始真近角f=135°~198°附近远地点高度始终减小。在各自的高能脉冲激光最佳作用区域，自旋碎片与非自旋碎片的远地点高度均减小，且自旋碎片的减小幅度明显大于非自旋碎片。
Figure 5. Apogee altitude vs. initial true anomaly
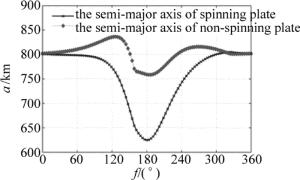
自旋碎片与非自旋碎片变轨后的半长轴随初始真近角的变化曲线如图 6所示。可以看出, 自旋碎片变轨后半长轴在初始真近角f=45°~180°附近始终减小，在初始真近角f=180°~225°附近持续增加；非自旋碎片变轨后半长轴在初始真近角f=45°~126°或f=186°~225°附近持续增大，在初始真近角f=126°~ 186°附近始终减小。自旋碎片与非自旋碎片的半长轴在最佳作用区域中均减小，同样自旋碎片半长轴的减小量明显大于非自旋碎片。
Figure 6. Semi-major axis vs. initial true anomaly
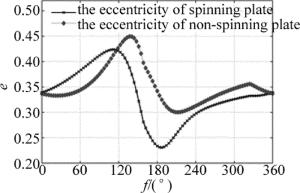
图 7是自旋碎片与非自旋碎片变轨后的偏心率随初始真近角的变化曲线。可以看出，自旋碎片变轨后偏心率在初始真近角f=45°~112°或f=187°~225°附近持续增加，在初始真近角f=112°~187°附近始终减小；非自旋碎片变轨后偏心率在初始真近角f=45°~ 137°或f=212°~225°附近持续增大，在初始真近角f=137°~212°附近始终减小。自旋碎片和非自旋碎片偏心率减小最大的区域均位于各自的最佳作用区域。
Figure 7. Eccentricity vs. initial true anomaly
-
针对LEO区域中常见的铝合金平板，分别建立了地基激光清除自旋空间碎片和非自旋空间碎片的动力学降轨模型，通过理论分析和仿真计算，对空间碎片轨道参量的变化情况进行了数值模拟，主要结论如下：地基激光清除空间碎片存在最佳作用区域，且自旋碎片的最佳作用区域更宽，自旋碎片在初始真近角86°~151°范围内降轨效果最佳，非自旋碎片在初始真近角130°~162°范围内降轨效果最佳；相同条件下，自旋空间碎片降轨效果明显优于非自旋空间碎片，更易于达到清除降轨的目的。
地基激光驱动空间碎片降轨特性研究
Research on de-orbiting mechanism of space debris driven by ground-based laser
-
摘要: 为了研究小尺度空间碎片的降轨特性，建立了空间碎片自旋与非自旋模型，理论分析了地基激光作用下碎片速度的变化规律，在此基础上研究了激光辐照作用下空间碎片的变轨模型。采用理论仿真的方法，分析了在高能脉冲激光作用下空间碎片的近地点与远地点高度、半长轴及偏心率随初始真近角的变化规律。结果表明，地基激光清除空间碎片存在最佳作用区域，自旋碎片在初始真近角86°~151°范围内降轨效果最佳，非自旋碎片在初始真近角130°~162°范围内降轨效果最佳。自旋空间碎片降轨效果明显优于非自旋空间碎片。Abstract: In order to stuy the de-orbiting mechanism of small scale space debris, the models of spinning and non-spinning space debris were established. The variation of space debris velocity ablating by ground-based laser was analyzed theoretically. Orbit maneuver mode of space debris irradiating by laser was investigated. The variations of perigee and apogee altitudes, semi-major axis and eccentricity with the change of initial true anomaly of the space debris under the irradiation of high-energy pulse laser were simulated and analyzed. The simulation results show that there is an optimal action area of removal of space debris using ground-based laser. The de-orbiting effect of spin debris is the best with initial true anomaly in the range of 86°~151°. The de-orbiting effect of non-spinning debris is the best with initial true anomaly in the range of 130°~162°. The de-orbiting effect of spinning debris is superior to non-spinning debris.
-
Key words:
- laser technique /
- space debris /
- ground-based laser /
- de-orbit /
- impulse coupling
-
Table 1. Laser parameters
parameter value range 1000km laser wavelength 1.06μm beam quality factor 2.0 efficiency factor 30% mirror diameter 13m laser spot radius 31cm laser pulse energy 7.3kJ fluence on target 53kJ/m2 laser repetition rate 11.2Hz 
下载: 导出CSV
Table 2. Physical parameters of space debris
space debris description Al/plate areal mass density 10kg/m2 mass 0.75kg angular velocity 2.5rad/s impulse coupling coefficient 75μN·s/J
下载: 导出CSV
-
[1] LI Ch L, OUYANG Z Y, DU H. Space debris and space environment[J]. Quaternary Sciences, 2002, 22(6): 540-551(in Chinese). [2] GONG Z Zh, XU K B, MU Y Q, et al. The space debris environment and the active debris removal techniques[J]. Spacecraft Environment Engineering, 2014, 31(2): 129-135(in Chinese). [3] APOLLONOV V V. High power lasers for space debris elimination[J]. Chinese Optics, 2013, 6(2): 187-195. [4] PHIPPS C, ALBRECHT U, FRIEDMAN H, et al. ORION: clearing near-earth space debris using a 20kW, 530nm, Earth-based, repetitively pulse laser[J]. Laser and Particle Beams, 1996, 14(1): 1-44. doi: 10.1017/S0263034600009733 [5] ESMILLER B, JACQUELARDB C. CLEANSPACE "small debris removal by laser illumination and complementary technologies"[C] //Beamed Energy Propulsion. AIP Conference Proceedings. New York, USA: American Institute of Physics, 2011: 347-353. [6] HONG Y J, JIN X, CHANG H. Discussion of key problems in space based laser centimeter orbital debris removal[J]. Infrared and Laser Engineering, 2016, 45(2): 0229001(in Chinese). doi: 10.3788/irla [7] CHANG H, JIN X, ZHOU W J. Experiment research on plasma plume expansion induced by nanosecond laser ablation Al[J].Infrared and Laser Engineering, 2013, 42(s1): 43-46 (in Chinese). [8] LU J Y, WANG J, MA Y G, et al. Theoretical simulations of the mechanical characteristics of laser induced plasma for monatomic target[J]. Optics and Precision Engineering, 2004, 12(5): 550-554(in Chinese). [9] CHANG H, JIN X, HONG Y J. Modeling and simulation on active space debris orbit maneuver based on laser ablation impulse coupling[J]. Acta Aeronautics et Astronautics Sinica, 2013, 34(10): 2325-2332(in Chinese). [10] JIN X, HONG Y J, CHANG H. Simulation analysis of removal of elliptic orbit space debris using ground-based laser[J]. Acta Aeronauticaet Astronautica Sinica, 2013, 34(9): 2064-2073(in Chinese). [11] FANG Y W, ZHAO Sh H, YANG L W, et al. Research on action rules of ground-based laser irradiating small scale space debris in LEO[J]. Infrared and Laser Engineering, 2016, 45(2): 229002(in Chinese). doi: 10.3788/irla [12] PHIPPS C R, BAKER K L, LIBBY S B, et al. Removing orbital debris with lasers[J]. Advances in Space Research, 2012, 49(9): 1283-1300. doi: 10.1016/j.asr.2012.02.003 [13] STEVERDING B, DUDEL H P. Laser-induced shocks and their capability to produce fracture[J]. Journal of Applied Physics, 1976, 47(5): 1940-1945. doi: 10.1063/1.322917 [14] LIEDAHL D A, RUBENCHIK A, LIBBY S B, et al. Pulsed laser interactions with space debris: Target shape effects[J]. Advances in Space Research, 2013, 52(5): 895-915. doi: 10.1016/j.asr.2013.05.019 -
点击查看大图
图(7) / 表(2)
计量
- 文章访问数: 5627
- HTML全文浏览量: 3482
- PDF下载量: 18
- 被引次数: 0
