网站地图
下载:
-
光学Tamm态(optical Tamm state, OTS)是在电子Tamm态的基础上提出的，所谓电子Tamm态是一种电子局域表面态，它是TAMM在20世纪30年代预言在截断的周期原子势边缘处会出现一种电子局域表面态，即电子Tamm态。1990年，OHNO等人在半导体超晶格中首次观测到Tamm态[1]，产生电子Tamm态的原因是由于晶格的不完整性使得周期势场在表面处中断, 造成电子波函数在晶体表面外侧和内侧均按指数形式衰减，使得电子局域在表面附近而形成电子Tamm态。近年来, 人们在光子晶体的研究中通过类比固体物理中的电子Tamm态, 提出了光学Tamm态的概念。光学Tamm态是一种电磁波的界面局域模[2-5]，远离该界面电磁场强度逐渐减弱。由于光学Tamm态特殊的物理性质，对它的研究逐渐成为光子晶体领域内的一个热点问题[6-12]。光学Tamm态高强度的电磁局域模式以及它对电磁波的完美吸收，可以在多个领域有着很好的应用前景, 如非线性效应、法拉第磁光效应增强、高灵敏光学传感器、荧光效应等。因此，对光学Tamm态的深入研究不仅具有重要的理论价值，而且具有重要的应用价值。
参考文献[13]和参考文献[14]中研究了“银-光子晶体-银”结构中的光学Tamm态特性，发现在银层与光子晶体的分界面上出现了两个光学Tamm态。在这些研究中银介电常数的色散模型对光学Tamm态计算结果有着重要的影响, 使用的银介电常数的色散模型越接近实验值，得出的光学Tamm态的性质越接近真实情况。参考文献[13]中采用的银介电常数的色散模型为εr= 1-ωep2/ω2, 其中ω和ωep分别为电磁波的角频率和金属薄膜中的等离子体频率。由于这一模型中银介电常数为实数，因此它只考虑了色散对银折射特性的影响而没有考虑色散对银吸收特性的影响，所以得出的光学Tamm态不能准确地反应真实情况。参考文献[14]中采用的银介电常数的色散模型为Drude模型，即εr=ε∞-ωep2/ω(ω+iν)2，研究了该结构的光学Tamm态特性，在这一模型中银介电常数为复数，它不仅考虑了色散对银折射特性的影响，而且也考虑了色散对银吸收特性的影响，但是该模型与银介电常数的实验值符合不够好[13]，因此得出的结论与光学Tamm态的真实情况也有差异。为了得到更接近光学Tamm态真实情况的性质，研究时应该采用与实验值符合得最好的模型。在目前常见的银介电常数的色散模型中, Drude-Lorentz色散模型与银介电常数的实验值符合最好[15]。由于Tamm态的吸收性质是一个具有重要理论意义和应用价值的问题[14]，因此本文中将采用银介电常数最好的色散模型——Drude-Lorentz模型来研究银-光子晶体-银结构中两种偏振光Tamm态的吸收特性。
-
设计一种银(M)-光子晶体(photomc crystal, PC)-银(M)结构，如图 1所示。其中1维光子晶体的结构为(aba)N，周期数N=10，每个周期的第1层与第3层是同种a介质，中间一层为b介质。a介质为氧化铝，其折射率和厚度分别为na =1.8和da=200nm; b介质为砷化钾，其折射率和厚度分别为nb=3.23和db=400nm。两边是厚度为dM的银层。
Figure 1. Structure of M-PC-M
银介电常数εr的Drude-Lorentz色散模型[15]为：
$ {\varepsilon _{\text{r}}} = {\varepsilon _\infty } - \frac{{{\omega _{\text{p}}}^2}}{{{\omega ^2} + {\text{i}}\omega \mathit{\gamma }}} - \frac{{\mathit{\Delta } \times {\mathit{\Omega }^{\text{2}}}}}{{({\omega ^2} - {\mathit{\Omega }^{\text{2}}}) + {\text{i}}\mathit{\Gamma }}} $
(1) 式中, ω为光的角频率, ε∞=2.4064, ωp=2π×2214.6×1012Hz, γ=2π× 4.8×1012Hz, Δ=1.6604, Ω=2π×1330.1×1012Hz, Γ=2π× 620.7×1012Hz。
银的复折射率${\widetilde n_{\text{M}}}$为：
$ {\widetilde n_{\text{M}}} = \sqrt {{\varepsilon _{\text{r}}}} = {n_{\text{M}}} + {\text{i}}\mathit{k} $
(2) 式中, 复折射率的实部nM描述银对光的折射特性，其虚部k称为消光系数，描述银对光的吸收特性。为了得到银复折射率的实部nM和虚部k随波长的变化特征，利用(1)式和(2)式计算出nM和k随波长λ的响应曲线，如图 2所示。由图 2可知：波长在360nm~2000nm范围内，nM由0.02逐渐增加到0.24，银的nM值很小，这是引起银对电磁波有很强反射作用的原因。波长在300nm~2000nm范围内，k由0逐渐增加到14，银的k值较大，这是引起银对电磁波有很强吸收作用的原因。银较大的消光系数也必然对银-光子晶体-银结构中TE波和TM波的Tamm态的吸收特性产生重大影响。
Figure 2. a—reflectivity nM vs. wavelength b—extinction coefficient k vs. wavelength
计算光通过银-光子晶体-银结构的反射率和透射率用特征矩阵法[16-17]，光在该结构中的特征矩阵M为：
$ \mathit{\boldsymbol{M = }}\left[ \begin{gathered} {M_{11}}\;\;\;{M_{12}} \hfill \\ {M_{21}}\;\;\;{M_{22}} \hfill \\ \end{gathered} \right] = {\mathit{\boldsymbol{m}}_{\text{M}}}{({\mathit{\boldsymbol{m}}_a}{\mathit{\boldsymbol{m}}_b}{\mathit{\boldsymbol{m}}_a})^\mathit{N}}{\mathit{\boldsymbol{m}}_{\text{M}}} $
(3) 其中,
$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{m}}_{\rm{a}}} = \left[ \begin{array}{l} \;\;\;\;\cos {\delta _{\rm{a}}}\;\;\;\;\; - {\rm{i}}{\mathit{p}_{\rm{a}}}^{ - 1}\sin {\delta _{\rm{a}}}\\ - {\rm{i}}{\mathit{p}_{\rm{a}}}\sin {\delta _{\rm{a}}}\;\;\;\;\;\;\;\cos {\delta _{\rm{a}}} \end{array} \right]\\ {\mathit{\boldsymbol{m}}_{\rm{b}}} = \left[ \begin{array}{l} \;\;\;\;\cos {\delta _{\rm{b}}}\;\;\;\;\; - {\rm{i}}{\mathit{p}_{\rm{b}}}^{ - 1}\sin {\delta _{\rm{b}}}\\ - {\rm{i}}{\mathit{p}_{\rm{b}}}\sin {\delta _{\rm{b}}}\;\;\;\;\;\;\cos {\delta _{\rm{b}}}\; \end{array} \right]\\ {\mathit{\boldsymbol{m}}_{\rm{M}}} = \left[ \begin{array}{l} \;\;\;\cos {\delta _{\rm{M}}}\;\;\;\; - {\rm{i}}{\mathit{p}_{\rm{M}}}^{ - 1}\sin {\delta _{\rm{M}}}\\ - {\rm{i}}{\mathit{p}_{\rm{M}}}\sin {\delta _{\rm{M}}}\;\;\;\;\;\;\cos {\delta _{\rm{M}}} \end{array} \right] \end{array} \right. $
(4) 式中，δi=(2π/λ)nidicosθi；对于TE波, ${p_i} = \sqrt {{\varepsilon _0}/{\mu _0}} \times {n_i}\cos {\theta _\mathit{i}}, $对于TM波, ${p_i} = \sqrt {{\varepsilon _0}/{\mu _0}} \times {n_i}/\cos {\theta _\mathit{i}}\left( {i = {\text{a}},{\text{b}},{\text{M}}} \right) $; λ为入射光的波长，θ为折射角，ε0为真空的介电常数，μ0为真空的磁导率。光的透射系数t和反射系数r分别为：
$ \left\{ \begin{gathered} t = \left| {\frac{{2{p_0}}}{{\left( {{M_{11}} + {M_{12}}{p_{\text{t}}}} \right){p_0} + \left( {{M_{21}} + {M_{22}}{p_{\text{t}}}} \right)}}} \right| \hfill \\ r = \left| {\frac{{\left( {{M_{11}} + {M_{12}}{p_{\text{t}}}} \right){p_0} - \left( {{M_{21}} + {M_{22}}{p_{\text{t}}}} \right)}}{{\left( {{M_{11}} + {M_{12}}{p_{\text{t}}}} \right){p_0} + \left( {{M_{21}} + {M_{22}}{p_{\text{t}}}} \right)}}} \right| \hfill \\ \end{gathered} \right. $
(5) 式中, 下标0表示入射空间、下标t表示透射空间，光的透射率T和反射率R分别为：
$ \left\{ \begin{array}{l} T = {p_{\rm{t}}}{t^2}/{p_0}\\ {\rm{R = }}{{\rm{r}}^{\rm{2}}} \end{array} \right. $
(6) 光通过该银-光子晶体-银结构的吸收率A为:
$ A = 1 - T - R $
(7) 利用(1)式~(7)式就可以研究该银-光子晶体-银结构中两种偏振光(TE波和TM波)Tamm态的吸收特性。
-
为了得出TE波和TM波的Tamm态，固定dM=40nm、入射角θ0=0.3rad, 利用(1)式~(6)式计算出TE波和TM波入射该银-光子晶体-银结构的透射率随波长的响应曲线，见图 3a和图 3b。在图 3a和图 3b中, 实线为该银-光子晶体-银结构的透射率随波长的响应曲线，虚线为该结构中间光子晶体的透射率随波长的响应曲线。由图 3中虚线可知, 波长在778nm~810nm范围内是光子晶体的禁带。由图 3a和图 3b中实线可知:TE波和TM波都在光子晶体的禁带内波长为784.5nm和786.1nm处出现了两个透射峰(双峰)，这两个透射峰就是由于加入银层后在前后银层与光子晶体的界面上产生的两个OTS[14-15]。将波长较小的光学Tamm态称为OTS1，将波长较大的光学Tamm态称为OTS2。从图 3中看出, TE波和TM波的Tamm态很相似，但是它们仍然存在着一定的差别，下面就研究TE波和TM波的Tamm态的吸收特性，并比较它们的异同。
Figure 3. a—TE transmissivity vs. wavelength b—TM transmissivity vs. wavelength
-
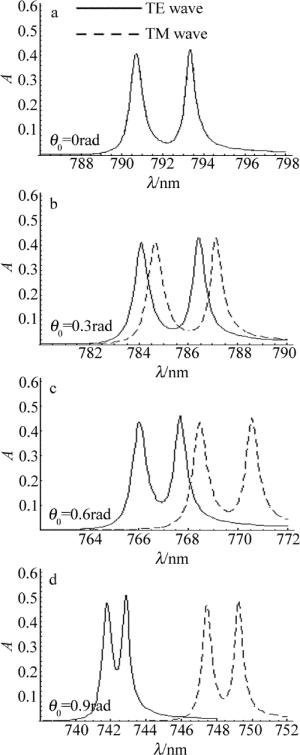
为了得到TE波和TM波Tamm态的吸收率随入射角的变化特性，固定dM=40nm，利用(1)式~(7)式计算出TE波和TM波在θ0=0rad, θ0=0.3rad, θ0=0.6rad, θ0=0.9rad 4种情况下其OTS的吸收率随波长的响应曲线，如图 4所示。由图 4可知：(1)当θ0=0rad时，TE波和TM波的OTS1和OTS2的吸收峰完全重合，随着入射角的增大, TE波和TM波OTS的中心波长都向短波方向移动，并且TE波和TM波的OTS1和OTS2的吸收峰逐渐分开; (2)当θ0=0rad时，TE波和TM波的OTS1和OTS2的吸收峰值分别为0.404和0.422, 随着入射角的增大，TE波和TM波的OTS1和OTS2的吸收峰值逐渐增大，但TM波的OTS1和OTS2的吸收峰值增加较慢; 当θ0=0.9rad时，TE波的OTS1和OTS2的吸收峰值分别增加为0.477和0.505，TM波的OTS1和OTS2的吸收峰值分别增加为0.461和0.572;(3)当θ0=0rad时，TE波和TM波的OTS1和OTS2的中心波长间距都为2.4nm, 随着入射角的增大，TE波和TM波的OTS1和OTS2的中心波长间距都减小，但TM波的OTS1和OTS2的中心波长间距减小较慢；当θ0=0.9rad时，TE波的OTS1和OTS2的中心波长间距减小为1.2nm，TM波的OTS1和OTS2的中心波长间距减小为1.9nm。
Figure 4. OTS absorptivity vs. incidence angle
-
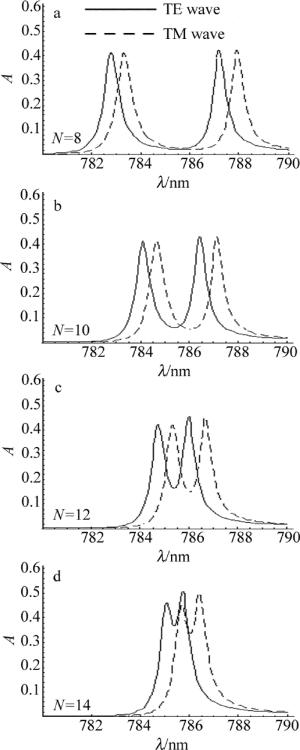
为了研究光子晶体的周期数对TE波和TM波Tamm态的吸收率的影响，固定θ0=0.3rad和dM=40nm，利用(1)式~(7)式计算出周期数N=8, N=10, N=12, N=14这4种情况下TE波和TM波OTS的吸收率随波长的响应曲线，如图 5所示。由图 5可知：(1)当N=8时，TE波和TM波的OTS1和OTS2的吸收峰值都分别为0.41和0.42, 随着周期数的增大, TE波和TM波的OTS吸收峰值都缓慢增加，TE波的OTS吸收峰值增加略快一些; 当N=14时，TE波的OTS1和OTS2吸收峰值分别增加为0.46和0.51，TM波的OTS1和OTS2吸收峰值分别增加为0.45和0.49;(2)当N=8时，TE波和TM波的OTS1和OTS2的中心波长间距都为4.4nm, 随着周期数的增大, TE波和TM波的OTS1和OTS2的中心波长间距同步减小; 当N=14时，TE波的OTS1和OTS2的中心波长间距都减小为0.7nm，TE波和TM波的OTS1和OTS2都几乎重合; (3)TE波和TM波的OTS的中心位置几乎不随周期数的增大而移动。
Figure 5. OTS absorptivity vs. number of cycles
-
为了研究银层厚度对TE波和TM波Tamm态的吸收率的影响，固定θ0=0.3rad和N=10，利用(1)式~(7)式计算出银层厚度dM=25nm, dM=35nm, dM=45nm, dM=55nm 4种情况下TE波和TM波OTS的吸收率随波长的响应曲线，如图 6所示。由图 6可知：(1)当dM=25nm时，TE波的OTS1和OTS2的吸收峰值分别为0.24和0.28，TM波的OTS1和OTS2的吸收峰值分别为0.23和0.27;随着银层厚度的增大, TE波和TM波的OTS吸收峰值明显增加；当dM=55nm时，TE波和TM波OTS1和OTS2的吸收峰值都增加为0.49;(2)当dM=25nm时，TE波的OTS1和OTS2的中心波长分别为786nm和788nm, TM波的OTS1和OTS2的中心波长分别为787nm和789nm; 随着银层厚度的增大, TE波和TM波的OTS1和OTS2的中心波长都缓慢减小；当dM=55nm时，TE波的OTS1和OTS2的中心波长分别减小为783.5nm和785.8nm, TM波的OTS1和OTS2的中心波长分别减小为784.4nm和786.8nm; (3)当dM=25nm时，OTS1和OTS2几乎重合，随着银层厚度的增大OTS1和OTS2的吸收峰变化得越来越窄，OTS1和OTS2的分离越来越明显。
Figure 6. OTS absorptivity vs. thickness of silver
-
研究了银介电常数的Drude-Lorentz色散模型中复折射率的特性，得到复折射率的实部和虚部随波长的变化规律。利用它研究了银-光子晶体-银结构中两种偏振光Tamm态的吸收率随入射角、随周期数以及随银层厚度的变化规律，得出以下结论：在银-光子晶体-银结构中两种偏振光(TE波和TM波)都会出现两个光学Tamm态，即OTS1和OTS2；两种偏振光的OTS1和OTS2吸收峰值随着入射角的增大而逐渐增大、随着周期数的增大而缓慢增大、随着银层厚度的增大而明显增大；两种偏振光OTS1和OTS2吸收峰的中心波长随入射角的增加向短波方向移动。
这些结果的获得丰富了对银-光子晶体-银结构中两种偏振光Tamm态的吸收特性的认识。并且利用光学Tamm态的这些特性可以实现对入射电磁信号的有效控制，这具有重要的应用价值。
金属-光子晶体-金属结构中偏振光Tamm态的吸收特性
Absorption properties of polarized light Tamm state in metal-photonic crystal-metal structure
-
摘要: 为了研究银-光子晶体-银结构中两种偏振光Tamm态的吸收性质，采用银介电常数的Drude-Lorentz色散模型和特征矩阵法，研究了吸收率随入射角、随周期数以及随银层厚度的变化规律。结果表明，在银-光子晶体-银结构中两种偏振光都会出现两个光学Tamm态（OTS），即OTS1和OTS2。两种偏振光的OTS1和OTS2的吸收峰值随着入射角的增大而逐渐增大，随着周期数的增大而缓慢增大，随着银层厚度的增大而明显增大。这些结论丰富了对银-光子晶体-银结构中两种偏振光Tamm态的吸收特性的认识。Abstract: In order to study absorption properties of Tamm state of two kinds of polarized light in silver-photonic crystal-silver structure, by using Drude-Lorentz dispersion model of silver dielectric constant and the characteristic matrix method, the variations of absorption rate with the change of incident angle, cycle number and silver layer thickness were studied. The results show that, two optical Tamm states would appear in two kinds of polarized lights in silver-photonic crystal-silver structure:OTS1 and OTS2. The absorption peak value would increase gradually with the increase of incidence angle, increase slowly with the increase of cycle number, and increase obviously with the increase of silver thickness. The study makes the deep understanding of absorption characteristics of Tamm state of two kinds of polarized light in silver-photonic crystal-silver structure.
-
Key words:
- materials /
- photonic crystal /
- optical Tamm state /
- Drude-Lorentz model /
- polarized light /
- absorption
-
[1] OHNO H, MENDEZ E E, BRUM J A, et al. Optical Tamm state on asymmetric DBR-metal structure[J].Physical Review Letters, 1990, 64(4):2555-2560. [2] KAVOKIN A V, SHELYKH I A, MALPUECH G. Lossless interface modes at the boundary between two periodic dielectric structures[J].Physical Review, 2005, B72(23):233102-233105. [3] GUO Y, SUN Y, ZHNAG Y. Experimental investigation of interface states in photonic crystal heterostructures[J]. Physical Review, 2008, E78(2):026607-026612. [4] KALITEEVSKI M, IORSH I, BRAND S. Tamm plasmon-polaritons:possible electromagnetic states at the interface of a metal and a dielectric bragg mirror[J]. Physical Review, 2007, B76(16):165415-165419. [5] BRAND S, KALITEEVSK M A, ABRAM R A. Optical Tamm states above the bulk plasma frequency at a bragg stack/metal interface[J].Physical Review, 2009, B79(8):085416-085419. [6] DURACH M, RUSINA A. Transforming Fabry-Pérot resonances into a tamm mode[J].Physical Review, 2012, B86(23):235312-235317. [7] CHUN Z H, GUANG Y, KAI W. Coupled optical tamm states in a planar dielectric mirror structure containing a thin metal film[J].Chinese Physics Letters, 2012, 29(6):067101-067104. doi: 10.1088/0256-307X/29/6/067101 [8] FANG Y T, YANG L X, ZHOU J. Tamm states of one-dimensional photonic crystal based on surface defect[J].Journal of Infrared and Millimeter Waves, 2013, 32(6):526-530(in Chinese). doi: 10.3724/SP.J.1010.2013.00526 [9] CHEN Z F, HAN P, CHEN Y H. Photonic band gap splitting based on optical Tamm states of photonic crystal[J].Acta Optica Sinica, 2012, 32(5):516002(in Chinese). doi: 10.3788/AOS [10] JIANG H L, LIU Q N. Field distribution of two kinds of polarized light in 1-D photonic crystal[J].Laser Technology, 2014, 38(5):718-722(in Chinese). [11] DAI H X, LIU Q N. Dispersion characteristics of defect mode in 1-D square doped photonic crystal waveguide[J].Laser Technology, 2013, 37(3):338-342(in Chinese). [12] JIANG Y Z, ZHANG G W, ZHU Y Y. Optical Tamm state theory study on asymmetric DBR-metal-DBR structure[J].Acta Physica Sinica, 2013, 62(16):167303(in Chinese). [13] CHEN L K, FANG Y T, ZHU N, et al. Implementation of tunable dual-band filter based on the coupling of tamm state of the 1-D photonic crystal[J]. Journal of Synthetic Crystals, 2013, 42(11):2406-2410(in Chinese). [14] LU S Q, CHAO X G, CHEN X F, et al. TE polarization perfect absorption with dual-band in metal-photonic crystal-metal structure[J].Acta Optica Sinica, 2015, 35(1):116003(in Chinese). doi: 10.3788/AOS [15] SU J, SUN C, WANG X Q. A metallic dispersion model for numerical simulation[J].Journal of Optoelectronics·Laser, 2013, 24(2):408-411(in Chinese). [16] LIU Q N, LIU Q. Transmission theory of photonic and phononic crystal[M].Beijing:Science Press, 2013:125-162(in Chinese). [17] LIU Q N, LIU Q. Light field dispersion effect of total reflection tunnel in 1-D photonic crystal[J].Laser Technology, 2014, 38(6):738-742(in Chinese). -
点击查看大图
图(6)
计量
- 文章访问数: 8614
- HTML全文浏览量: 6567
- PDF下载量: 422
- 被引次数: 0
