网站地图
下载:
-
冰洲石空气隙型格兰-泰勒棱镜抗光损伤能力强，长度孔径比相对小，消光比通常优于10-5，偏光性能和透射性能均佳[1]，尤其是良好的光透射性能更为棱镜在工程技术中的应用提供了保障[2-5]，它是目前国内外激光偏光技术中普遍采用的重要器件，在光纤通讯、激光调制、光信息处理、生物组织研究[6-7]以及其它许多领域[8]获得了广泛应用。偏光器件最重要的质量技术指标之一是消光比，而表征消光比这一指标的是最大透射光强和最小透射光强参量，故在测量这些参量过程中，对最大光强和最小光强取极点的精确定位测量方法以及测量值的动态范围选择就极为重要。为此有人曾对格兰-泰勒棱镜的光强透射比做了较详细研究[[9-11]。理论上光强透射比会随入射角的变化而连续变化，但发现在斜入射情况下，光强透射比曲线并不是完全按照余弦平方曲线规律变化，而是在曲线上出现了一些上下的波动状况[12]，这就导致了最大透射光强采集的不稳定性，影响了棱镜消光比的测量精度。实验表明，晶体斜入射情况对应器件的不同轴性，这在偏光器件制造和使用过程中是不可避免的，作者借此通过对棱镜入射端、出射端、胶合层反射及透射情况的分析，以不同角度入射格兰-泰勒棱镜的情况来解释其干扰发生的程度，并采用二次曲线拟合方法对透射光强最大点进行判断，消除干涉波动的影响，以此提高测量棱镜消光比的精度。
-
对于偏光镜的消光比，定义为：ρ=T2/T1。其中，T1和T2统称为主透射比，通常表述为入射光在偏光镜主截面内的振动分量的透射比；但T1是棱镜的最大透射比，T2是棱镜的最小透射比，也就是入射光中与偏光镜主截面垂直的振动方向分量的透射比。如果有一个好的线偏振光源，其消光比要高于待测棱镜至少2个数量级，则测量消光比的系统会相应简练。从高消光比起偏器透射出的光直接入射待测棱镜，待测棱镜以光线为轴慢慢旋转，透射待测棱镜的光经过放大及信噪比处理等手段，可以获得极大值T1和极小值T2，从而定出待测偏光镜的消光比ρ。
格兰-泰勒棱镜由两块方解石晶体三角棱镜组合而成，棱镜斜面间垫一个中间有孔的垫片形成空气层，这样入射光束就会经历前、后、中间4个晶面的反射及透射影响。理想情况下，当一束单色光垂直棱镜端面入射，晶体光轴的方向平行于棱镜的表面，光进入棱镜后垂直于晶体光轴方向传播，o光和e光并不分开，但其传播速度不同，对应折射率不同，到达空气隙界面，o光全反射，出射光仅为e光，由于讨论的入射角度比较小，棱镜的半视场角不大于±3°，所以把e光波的折射率做近似处理，取其主折射率值，即ne′=ne[13]，依此分析光束在棱镜各晶面上的光强透射比。
当光束以一定角度斜入射时，入射到待测棱镜上的线偏振光的电矢量振动方向与棱镜的主截面之间的夹角，即为调制角α，理论上讲满足马吕斯定律[14]，棱镜的光强透射比为：
$ T = A{T_1}{\rm{co}}{{\rm{s}}^2}\alpha $
(1) 式中, A为光束垂直入射到棱镜入射端面上、入射端面和出射端面的光强透射系数[15]:
$ A = {\left[ {\frac{{4{n_{\rm{e}}}}}{{{{(1 + {n_{\rm{e}}})}^2}}}} \right]^2} $
(2) 即A是ne的函数，ne取值为1.48518[16]，所以前后端面透射系数A近似认为是常数。
T1为胶合层斜面的光强透射系数：
$ {T_1} = \frac{1}{{1 + FN}} $
(3) 式中，F为振幅调制因子，N为周期调制因子。
$ F = \frac{{4R}}{{{{\left( {1 - R} \right)}^2}}} $
(4) 由(4)式看出，F是R的函数，R为棱镜胶合层的光强反射比。
众所周知，棱镜中e光的振动方向对应于菲涅耳公式中的p振动分量，那么光束在棱镜斜面上的光强反射比为[17]:
$ R = {\left( {\frac{{{n_{\rm{e}}}{\rm{cos}}{\theta _4} - n{\rm{cos}}{\theta _3}}}{{{n_{\rm{e}}}{\rm{cos}}{\theta _4} + n{\rm{cos}}{\theta _3}}}} \right)^2} $
(5) 式中, n为空气的折射率，θ3和θ4为两个胶合层斜面上的入射角。
$ {\rm{cos}}{\theta _3} = \frac{1}{{{n_{\rm{e}}}}}(\sqrt {{n_{\rm{e}}}^2 - {\rm{si}}{{\rm{n}}^2}{\theta _1}} {\rm{cos}}S + {\rm{sin}}S{\rm{sin}}{\theta _1}{\rm{cos}}\alpha ){\rm{ }} $
(6) $ \begin{array}{l} {\rm{cos}}{\theta _4} = \\ \frac{{\sqrt {{n^2} - {n_{\rm{e}}}^2 + {{(\sqrt {{n_{\rm{e}}}^2 - {\rm{si}}{{\rm{n}}^2}{\theta _1}} {\rm{cos}}S + {\rm{sin}}S{\rm{sin}}{\theta _1}{\rm{cos}}\alpha )}^2}} }}{n} \end{array} $
(7) 式中, θ1为棱镜入射端面的入射角, S为结构角。
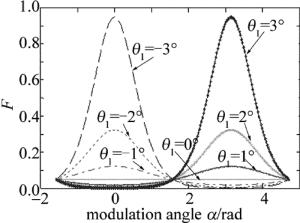
由(4)式~(7)式可以做出棱镜的F-α曲线，比较直观地反映出斜入射对振幅调制因子的影响，如图 1所示。图 1中纵坐标表示归一化的振幅调制因子, 它的变化直接影响到透射振幅，各入射角度曲线由不同线型加以区别。由图 1可以看出，F受α的影响，入射角度的绝对值越大影响越大。图中出现两个极大值点，两个极值的差(第二峰值-第一峰值)与斜入射角度成单调关系，且它的正负即是入射角方向，由此可以矫正晶体的方位使得入射角减小。
Figure 1. F-α curve
对于周期调制因子N，根据层间干涉分析得:
$ N = {\rm{si}}{{\rm{n}}^2}\left( {\frac{\delta }{2}} \right) = {\rm{si}}{{\rm{n}}^2}\left( {\frac{{2{\rm{ \mathsf{ π} }}h{\rm{cos}}{\theta _4}}}{{{\lambda _0}}}} \right) $
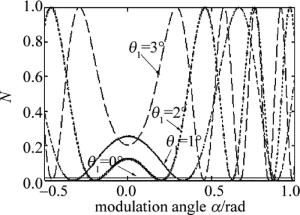
(8) 式中, δ为从空气隙中透射的两相邻光束的位相差，h为空气隙的厚度，这里以实际空气隙厚度26μm进行分析。由(7)式、(8)式可以做出N-α的曲线，如图 2所示。由图 2也可以清晰地看出周期调制因子N与调制角α的关系，周期调制因子对波动大小所起到的作用随着入射角的增大，周期逐渐减小。
Figure 2. N-α curve
令:
$ M = FN $
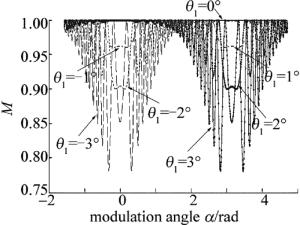
(9) 根据上述各式做出M-α曲线，如图 3所示。图 3为同一棱镜在光学系统中以不同入射角入射时，周期调制系数M对应的理论仿真曲线，纵坐标为归一化的振幅比例系数。由图可见，不同入射角入射的情况下，曲线波动幅度的大小、波动出现的位置等都不相同，但当光束在端面法线上侧以某一角度入射时，也就是正角度入射时，曲线在前面出现波动，但后面就波动很小。反之，如果负入射，前面几乎不变，但后面出现波动。此外还可以发现，入射角度越大，曲线波动越明显，这种变化的周期为2π。这种情况类似于待测棱镜在系统转动中的不同轴性，棱镜的轴线与入射光线不重合。
Figure 3. M-α curve
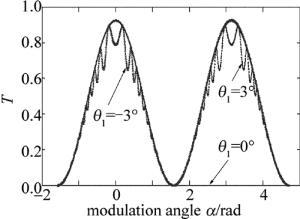
为了说明振幅调制因子F及周期调制因子N对棱镜透射比T的综合影响效果，作者由(1)式进行仿真，结果如图 4所示。这是特别选定的3条曲线，一条是垂直入射的中心曲线，即棱镜与系统完全同轴的情况，另两条是视场角边缘入射的曲线，视场角外入射已经不符合马氏定律，其它情况介乎于这3种情况之间。
Figure 4. T-α curve
图 4是入射角θ1为0°和°±3°时的光强透射比曲线。不同入射角入射的情况下，曲线波动幅度的大小、波动出现的位置等都不尽相同，垂直入射时没有波动。同时也清楚看到，当正入射时，棱镜透射曲线前半周期输出是有波动的，而后半个周期输出平稳；当光束负角度入射时，透射曲线与前述正相反，但振荡幅度是相同的。这种现象正好对应待测棱镜旋转规律的变化，在斜入射棱镜情况下，当出现光强振荡输出时，绕棱镜中心轴旋转棱镜π角度后仍将出现震荡输出，除非将棱镜轴调整到与入射光线重合或平行状态。
通过以上分析知道，当入射光束与棱镜成一定倾斜角度时，所测棱镜透射光强是不稳定的，透射光强随着棱镜旋转角改变呈波动输出状态，这样就无法精确定位最大光强的位置与大小，进而影响到消光比的精确测量。
-
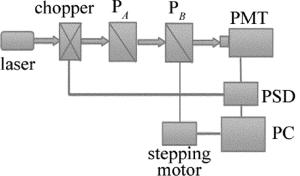
建立如图 5所示测量系统，该系统光源利用532nm激光器，一束平行的单色光束依次通过图示中各个光学器件，斩光器把连续光源发出的光信号调制成按对称方波变化的光信号，便于之后的光电变换后进行选频放大和相干检测，不仅能对被测光进行调制，还可以输出与调制频率同步的参考电压方波，作为锁相放大器的参考信号，出射光经起偏器PA后变为线偏振光，出射线偏振光入射到检偏器PB上，检偏器可随高精度步进电机旋转，从而使检偏器的透振方向与起偏器的偏振方向之间的夹角连续变化。透射的光强可由光电倍增管(photomultiplier tube, PMT)接收，经锁相放大器(phase sensitive detector, PSD)精确地测量被淹没在噪声、干扰背景中的微弱信号，采集后输入计算机(personal computer, PC)处理，进而得到检偏器的光强透射比随旋转角的变化曲线。
Figure 5. Experiment device
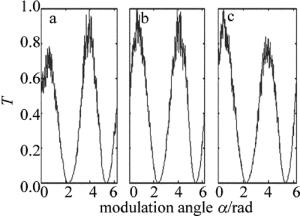
测量时由计算机控制步进电机带动检偏器旋转，使得调制角α在0°~360°连续改变，采样步长为设定角度，分别对3个样品进行光强的数据采集扫描采样，如图 6中的T-α透射曲线所示。
Figure 6. The measured data of T-α curve of three samples
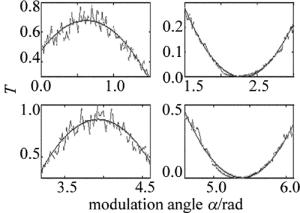
由图 6可以清楚看出，由于入射方位的偏差及棱镜装配同轴性偏差因素，透射曲线确实是振荡的，且在极大峰处起伏表现尤为明显，输出的最大数据位置并不一定是曲线的极大值位置，这也导致了前后半个周期极大值采点位置不一定是π，表面上看似违背了马氏定律。图 6a和图 6c中两个极大峰值相差较大，这一点同时也提醒人们，若调制棱镜入射方位角偏差大，需要重新调整，直到扫描曲线出现最大峰相差不大为止。对其4个极值点进行分段二次多项式拟合，以便更精确确定极值点的位置，如图 7所示。与理论对照发现，由于拟合结果只是确定了极值点的位置，其拟合极大值并不是透射的实际最大值，这个拟合极大值应该是图 4上包络线的极值，因此需要调整待测棱镜回到极值点位置，并配合入射光调整再测量光强，这个光强就是透射光强的极大值或极小值。
Figure 7. The fitting data of T-α curve
-
偏光棱镜是高消光比的器件，作为起偏器使用是非常理想的，但作为检偏器使用，输出的稳定性就需要特别关注，这一方面靠棱镜的精准装配，另一方面使用方法也非常重要。实验研究表明，棱镜检偏器中的空气隙型棱镜最易受此干扰，有胶层的棱镜干扰不明显。空气隙型棱镜主要为满足高功率激光设计的，短波长透过率相对来讲较高，是非常普遍使用的高性能器件。根据上述理论分析和实验证明，作为检偏器使用时，只要控制好入射角度就能基本发挥出它的优越性。依据理论分析知道，如果出现输出不稳定现象，这一般是在实验过程中棱镜放置不正确，根据实验曲线需要进一步调整方位。此研究另一个创新点是比较合理地解释了棱镜消光比测量过程中起偏器与检偏器旋转偏离马氏定律的问题，这在使用偏振片作为起偏器和检偏器系统中是不存在的，实验数据的二次分段拟合找准了调整角度极值点的位置，配合透射光强的二次测量，提高了消光比的测量精度。
干涉因素对偏光棱镜消光比测量的影响
Influence of interference factors on extinction ratio measurement of polarizing prism
-
摘要: 为了消除不同角度入射格兰-泰勒棱镜时透射光谱曲线波动干扰产生的影响，提高消光比测量系统的测量精度，以偏光棱镜作为检偏器，采用二次曲线拟合的方法，对透射曲线的极值点实现了精确判定。并采用二次光强测量方法，对棱镜入射端、出射端、胶合层反射及透射情况进行了理论分析，然后用不同角度入射时棱镜透射谱线的变化规律来解释其干扰发生的程度。结果表明，该方法消除了波动干扰影响，提高了测量棱镜消光比的精度。这一结果解决了空气隙型偏光棱镜消光比测量精度问题，同时对偏光棱镜的正确使用提供了参考建议。Abstract: In order to eliminate Glan-Taylor prism transmission spectra curve fluctuation and improve the measurement accuracy of extinction ratio, the quadratic curve fitting method was adopted to confirm the extreme point position of transmission curve by using polarizing prism as analyzer. The secondary light intensity was measured. And the incident end and transmission end of prism, reflection end and exit end of the cementing layer were analyzed theoretically. Then, variation law of the transmission spectrum of prism at different angles was used to explain the degree of interference. The measurement results show that this method eliminates the wave interference effect and improves the accuracy of the extinction ratio. The results solve the measurement accuracy problem of extinction ratio of air-spaced polarization prisms, and it provides the reference to use polarizing prism correctly.
-
Key words:
- physical optics /
- extinction ratio /
- curve fitting /
- polarizing prism
-
[1] TAKUBO Y, TAKEDA N, HUANG J H, et al. Precise measurement of the extinction ratio of a polarization analyzer[J]. Measurement Science & Technology, 1998, 9(1):20-23. [2] BASS M. Handbook of optics[M]. 3rd ed. New York, USA:McGraw-Hill, 1995:17-52. [3] APPEL R K, DYER C D, LOCKWOOD J N. Design of a broadband UV-visible v-barium borate polarizer[J]. Optica Applicata, 2002, 41(13):2470-2480. [4] DING P, CAO Y H, SU G Q, et al.1 kw high power diode laser with polarization coupled by Glan-Taylor prism[J]. Chinese Journal of Lasers, 2009, 36(2):290-293(in Chinese). doi: 10.3788/JCL [5] DONG L, ZHUO Zh, ZHAO Sh Zh. Analysis of factors affecting extinction ratio about double-crystal electro-optic switch[J]. Laser Technology, 2008, 32(1):15-17(in Chinese). [6] SANKARAN V, EVERETT M J, DUNCAN J, et al. Comparison of polarized light propagation in biological tissue and phantoms[J]. Optics Letters, 1999, 24(15):1044-1046. doi: 10.1364/OL.24.001044 [7] TOLGUENECE G L, DEVAUX F, LANTZ E. Two-dimensional time-resolved direct imaging though thick biological tissues:a new step toward noninvasive medical imaging[J]. Optics Letters, 1999, 24(15):1047-1049. doi: 10.1364/OL.24.001047 [8] SCHMITT J F, GANDJBAKHCHE A H, BONNER R F. Use of polarized light to discriminate short-path photons in a multiply scattering medium[J]. Applied Optics, 1992, 31(30):6535-6545. doi: 10.1364/AO.31.006535 [9] FAN J Y, LI H X, WU F Q. A study on transmitted intensity of disturbance for air-spaced Glan-type polarizing prisms[J]. Optics Communications, 2003, 223(s1/s3):11-16. [10] ZHU H F, SONG L K, WU F Q, et al. Cause of "minute fluctuation" on the transmission curve of taylor polarizing prism[J]. Chinese Journal of Lasers, 2004, 31(4):41-44(in Chinese). [11] LI H X, WU F Q, FANG J Y, et al. An analytical study on modulated intensity's perturbance for the polarizing prisms[J]. Journal of Optics, 2003, 23(12):1456-1459(in Chinese). [12] BI J. Polarizing prism transmittance incident angle effect[D]. Qufu: Qufu Normal University, 2007: 18(in Chinese). [13] LIU K Y, FANG R Y. Optics[M]. Beijing:Science and Technology of China Press, 1994:1(in Chinese). [14] LI J Zh. Handbook of optics[M]. Xi'an:Shaanxi Science and Technology Press, 1985:501(in Chinese). [15] ZHU H F. The influence of laser polarizing prism of output light intensity[D]. Qufu: Qufu Normal University, 2003: 21(in Chinese). [16] MU T K, LI G H, PENG H D. Study of the attenuator for the high extinction ratio testing system[J]. Laser Technology, 2007, 31(1):71-73(in Chinese). [17] CHENG G X, LI G H, PENG H D, et al. An automatic measurement system for extinction ratio in visible spectrum based on correlation detection principle[J]. Laser Technology, 2006, 30(2):161-164(in Chinese). -
点击查看大图
图(7)
计量
- 文章访问数: 7961
- HTML全文浏览量: 5815
- PDF下载量: 442
- 被引次数: 0
