网站地图
-
高光谱图像具有较高的光谱分辨率，能提供地物更为详尽的光谱信息，因此它能够更好地用于遥感影像的分类和目标识别[1]。与此同时，由于高光谱传感器较低的空间分辨率，混合像元在高光谱图像中普遍存在[2]。端元提取和光谱解混是混合像元线性分解的两大核心任务，而端元提取又是混合像元分解的前提[3]。典型的端元提取算法主要可分为3种类型：基于投影的方法，如纯净像元指数法[4](pure pixel index, PPI)；基于单形体体积的方法，如N-FINDR[5]、单形体体积增长算法[6](simplex growing algorithm，SGA)等；基于统计误差最小的方法，如迭代误差分析[7](iterative error analysis，IEA)。上述端元提取算法都只考虑了遥感图像中像元的光谱特征，把数据当作是光谱测量的一个无序列表而不是作为一幅图像来处理。事实上，端元在空间上的分布上应当具有一定的形状和集聚性，仅仅利用光谱特征来提取端元会忽略图像中的空间信息[8]。PLAZA等人将形态学算子引入到高光谱图像处理中，提出了自动形态学端元提取(automated morphological endmember extraction，AMEE)算法[9]，充分利用了图像的空间信息。
自动形态学端元提取算法由于将像元的光谱特征和空间特征结合在一起考虑，取得了很好的效果，然而该方法也存在一些缺陷。首先，AMEE算法在定义形态学算子时将结构元素内所有像元的平均值作为混合程度最大的像元，然而当结构元素内包含较多纯像元时，像元的均值也更加接近纯像元，那么膨胀和腐蚀运算就无法得到预期的结果。其次，原有的形态学离心率指数(morphological eccentricity index，MEI)表示结构元素内最纯像元与混合程度最大像元的光谱夹角距离，而不同结构元素内混合程度最大的像元一般是不同的，因此MEI的绝对大小无法真正代表像元的纯度。最后，算法中从每个结构元素内只选出一个像元作为候选端元，当结构元素内包含两个或两个以上不同物质的纯像元时就可能造成重要像元的遗失。
针对AMEE算法存在的局限性，通过引入参考光谱向量的概念计算得到整幅图像中混合程度最大的像元，在此基础上定义了改进的形态学算子，并给出了新的MEI计算方法。对原有的结构元素进行改进，用偶数大小结构元素取代奇数大小的结构元素，从每个结构元素内选出4个候选端元，有效避免了可能的信息遗失。最后，本文中提出了一种从上述3个方面改进的基于自动形态学的端元提取算法。将改进算法应用于高光谱数据并与仅从各自单方面进行改进的方法以及原算法对比，结果证明了从以上3个方面进行改进的必要性以及综合改进算法的有效性。
-
自动形态学端元提取算法将传统形态学理论进行了拓展定义，给出了应用于高光谱图像的膨胀和腐蚀操作，并且提出了根据像元的纯度进行排序的方法。根据凸面几何理论，纯净像元落于凸面单形体的顶面上，而混合程度较高的点则集中在凸面单形体的中心。因此，通过比较像元之间的空间距离来推断它们在凸面单形体中的相对位置，获得每一个像元的纯度信息，并以此作为依据进行排序[10]。
一般采用光谱夹角距离(spectral angel distance，SAD)来计算多维向量之间的距离。假设V1, V2, …, Vn是某个像素空间邻域内的一组多维向量，其中任意两个向量可以用Va和Vb表示，则它们的光谱夹角距离的弧度表示为：
$ {D_{{\rm{SAD}}}}\left( {{\mathit{\boldsymbol{V}}_a},{\mathit{\boldsymbol{V}}_b}} \right) = \arccos \left( {\frac{{{\mathit{\boldsymbol{V}}_a} \cdot {\mathit{\boldsymbol{V}}_b}}}{{\left\| {{\mathit{\boldsymbol{V}}_a}} \right\| \cdot \left\| {{\mathit{\boldsymbol{V}}_b}} \right\|}}} \right) $
(1) 将结构元素内每个像元与结构元素中心的光谱夹角距离作为排序准则。用cK表示结构元素K的中心，其定义如下：
$ {c_\mathit{\boldsymbol{K}}} = \frac{1}{M}\sum\limits_s {\sum\limits_t {f\left( {s,t} \right)} } ,\left( {\forall \left( {s,t} \right) \in \mathit{\boldsymbol{K}}} \right) $
(2) 式中，M为结构元素中的像元数量，(s, t)表示K中任一像元的坐标。
结构元素K内某一个像元f(x, y)到该结构元素的中心的距离为：
$ D\left( {f\left( {x,y} \right),\mathit{\boldsymbol{K}}} \right) = {D_{{\rm{SAD}}}}\left( {f\left( {x,y} \right),{c_\mathit{\boldsymbol{K}}}} \right) $
(3) 此时，相应的拓展形态学膨胀和腐蚀运算分别定义为[9]：
$ \begin{array}{*{20}{c}} {d\left( {x,y} \right) = \left( {f \otimes \mathit{\boldsymbol{K}}} \right)\left( {x,y} \right) = }\\ {\arg \_\min \left\{ {D\left( {f\left( {x + s,y + k} \right),K} \right)} \right\},\left( {\left( {s,t} \right) \in \mathit{\boldsymbol{K}}} \right)} \end{array} $
(4) $ \begin{array}{*{20}{c}} {e\left( {x,y} \right) = \left( {f \oplus \mathit{\boldsymbol{K}}} \right)\left( {x,y} \right) = }\\ {\arg \_\min \left\{ {D\left( {f\left( {x - s,y - t} \right),K} \right)} \right\},\left( {\left( {s,t} \right) \in \mathit{\boldsymbol{K}}} \right)} \end{array} $
(5) 式中，$ \otimes $和$ \oplus $分别表示膨胀和腐蚀运算。
PLAZA提出利用形态学离心率指数来表示结构元素中纯净像元的纯度。MEI为结构元素中纯度最高的像元与混合程度最高的像元之间光谱夹角距离，其计算方法如下：
$ {I_{{\rm{MEI}}}}\left( {n,m} \right) = {D_{{\rm{SAD}}}}\left( {d\left( {x,y} \right),e\left( {x,y} \right)} \right) $
(6) 得到高光谱数据的MEI图像后，利用阈值分割方法[11]选取MEI较大的像元作为图像的端元。
-
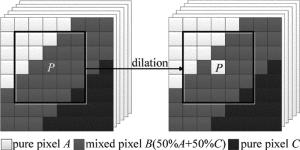
AMEE算法认为结构元素的中心一定是混合像元，通过膨胀和腐蚀运算可以获得局部邻域内最纯净和混合程度最大的像元，然而实践表明，膨胀运算得到的并不一定是纯净像元，对于腐蚀运算也是一样[12]。如果在图像的某个小范围内聚集了大量同种物质的纯净像元，那么该局部范围内像元的中心也即平均光谱更接近于纯净像元，而非混合像元，这时膨胀和腐蚀运算就不能得到预期的结果。为了保证拓展的膨胀和腐蚀运算能够得到正确的结果，需要对它们的定义进行改进。
首先定义图像的参考光谱向量Uben。参考光谱向量是最接近整幅图像中混合程度最大像元的向量，位于高光谱图像数据构成的单形体的最中心位置。Uben可以采用其它端元提取算法，如单形体体积增长算法、正交子空间投影(orthogonal subspace projection，OSP)算法[13]等提取到的图像端元的平均值，也可以用图像所有像元的平均值代替[12]。在无法确定其它端元提取算法的提取效果时，一般取图像中所有像元的平均值作为参考光谱向量。
结构元素K内某一个像元f(x, y)到参考光谱向量Uben的距离为：
$ {D_{\rm{m}}}\left( {f\left( {x,y} \right),\mathit{\boldsymbol{K}}} \right) = {D_{{\rm{SAD}}}}\left( {f\left( {x,y} \right),{\mathit{\boldsymbol{U}}_{{\rm{ben}}}}} \right) $
(7) 根据(7)式给出的新的距离公式可以定义改进的形态学算子。分别用dm(x, y)和em(x, y)表示利用改进的膨胀和腐蚀运算得到的像元，具体计算方法如下：
$ \begin{array}{*{20}{c}} {{d_{\rm{m}}}\left( {x,y} \right) = \left( {f \otimes \mathit{\boldsymbol{K}}} \right)\left( {x,y} \right) = }\\ {\arg \_\max \left\{ {{D_{\rm{m}}}\left( {f\left( {x + s,y + k} \right),\mathit{\boldsymbol{K}}} \right)} \right\},\left( {\left( {s,t} \right) \in \mathit{\boldsymbol{K}}} \right)} \end{array} $
(8) $ \begin{array}{*{20}{c}} {{e_{\rm{m}}}\left( {x,y} \right) = \left( {f \oplus \mathit{\boldsymbol{K}}} \right)\left( {x,y} \right) = }\\ {\arg \_\min \left\{ {{D_{\rm{m}}}\left( {f\left( {x - s,y - t} \right),\mathit{\boldsymbol{K}}} \right)} \right\},\left( {\left( {s,t} \right) \in \mathit{\boldsymbol{K}}} \right)} \end{array} $
(9) 改进后，膨胀和腐蚀运算分别可以得到结构元素内与参考光谱向量距离最大以及最小的像元。由于参考光谱向量代表图像中混合程度最大的像元，所以改进后的膨胀和腐蚀算子始终能够得到预期的结果。
将改进前后的膨胀算子应用于模拟高光谱图像，以便验证改进膨胀算子的效果。用光谱波段数为50的4个纯像元构建大小为200pixel×200pixel的模拟图像，其中4个纯像元区域大小为10像元×10像元，模拟高光谱数据第10波段的图像如图 1a所示。结构元素从3×3开始依次增大直至9×9，分别用改进前后的膨胀算子对模拟图像进行4次膨胀运算，图 1b表示改进前膨胀效果，图 1c表示改进后膨胀效果。可以看出，改进前的膨胀运算在某些地方并不能保证纯像元替代混合像元，所以在扩大后的纯像元区域内部出现了混合像元。而改进后的膨胀运算由于引入参考光谱向量保证了每次都能得到结构元素内最纯净的像元，因此能够得到正确的结果。
Figure 1. Comparison on dilation results of simulation image
-
AMEE算法中定义形态学离心率指数为结构元素内最纯净像元与混合程度最大的像元间的光谱夹角距离，并用它的大小来代表像元的纯净度。在不同结构元素内，根据腐蚀运算得到的混合程度最大的像元一般是不同的，那么不同结构元素内最纯净像元的形态学离心率指数代表的是它们相对于不同像元的光谱夹角距离。也就是说，不同结构元素内最纯净像元的形态学离心率指数的参照标准是不同的，不能简单地依据MEI的大小来判定两个像元纯净度的大小。为了使不同像元的形态学离心率指数之间具有可比性，作者重新定义了改进的MEI的计算方法：
$ {I_{{\rm{MEI,m}}}}\left( {n,m} \right) = {D_{{\rm{SAD}}}}\left( {d\left( {x,y} \right),{\mathit{\boldsymbol{U}}_{{\rm{ben}}}}} \right) $
(10) 上式中用结构元素内最纯净像元与参考光谱向量间的光谱夹角距离来表示不同像元的纯净度。由于对于整幅图像来说参考光谱向量是唯一的，因此, 不同结构元素内最纯净像元的形态学离心率指数就具有了可比性，改进的MEI越大，则该像元越纯净。
-
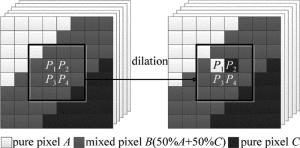
在自动形态学端元提取算法中，每次迭代结束时都对原始图像进行膨胀操作，并将膨胀结果作为下一次迭代运算的原始图像。通过不断的膨胀运算，图像中纯净的像元被保留下来，且越来越多，这有利于后续的端元提取。随着结构元素的不断增大以及纯净像元的增多，每个结构元素内可能包含两个甚至两个以上不同物质的纯净像元。然而，由于AMEE算法中结构元素的大小一般为奇数，每次膨胀操作只能将结构元素内最纯净的一个像元保留下来，这样必然导致其中一些物质的纯净像元被遗失。
图 2中给出了结构元素改进前，也即结构元素大小为奇数时的膨胀操作示意图。对于某一像元P，利用大小为5×5的结构元素对其进行膨胀操作，在该结构元素内包含A和C两种纯净像元，以及由它们混合而成的混合像元B。根据现有的膨胀运算计算公式，执行膨胀操作后像元P所在位置的混合像元B被纯净像元A所取代，而同样为纯净像元的C却被遗失。如果整幅图像中纯像元C的数量比较少，那么经过多次膨胀操作后图像中可能不再含有像元C，最后也不能正确地提取到图像的端元。
Figure 2. Diagram of dilation operation with original structure element
为了使图像的纯净像元都尽可能地被保留下来，尝试对结构元素的形状进行修正。选取大小为偶数的结构元素，并计算出结构元素内最纯净的4个像元d1, d2, d3, d4，它们的计算公式如下：
$ \begin{array}{*{20}{c}} {{d_1}\left( {{x_1},{y_1}} \right) = \left( {f \otimes \mathit{\boldsymbol{K}}} \right)\left( {{x_1},{y_1}} \right) = }\\ {\arg \_\max \left\{ {{D_{\rm{m}}}\left( {f\left( {{x_1} + s,{y_1} + t} \right),\mathit{\boldsymbol{K}}} \right)} \right\},\left( {\left( {s,t} \right) \in \mathit{\boldsymbol{K}}} \right)} \end{array} $
(11) $ \begin{array}{*{20}{c}} {{d_2}\left( {{x_2},{y_2}} \right) = \left( {f \otimes \mathit{\boldsymbol{K}}} \right)\left( {{x_2},{y_2}} \right) = }\\ {\arg \_\max \left\{ {{D_{\rm{m}}}\left( {f\left( {{x_2} + s,{y_2} + t} \right),\mathit{\boldsymbol{K}}} \right)} \right\},}\\ {\left( {\left( {s,t} \right) \in \left\{ {\mathit{\boldsymbol{K/}}\left\{ {\left( {{x_1},{y_1}} \right)} \right\}} \right\}} \right)} \end{array} $
(12) $ \begin{array}{*{20}{c}} {{d_3}\left( {{x_3},{y_3}} \right) = \left( {f \otimes \mathit{\boldsymbol{K}}} \right)\left( {{x_3},{y_3}} \right) = }\\ {\arg \_\max \left\{ {{D_{\rm{m}}}\left( {f\left( {{x_3} + s,{y_3} + t} \right),\mathit{\boldsymbol{K}}} \right)} \right\},}\\ {\left( {\left( {s,t} \right) \in \left\{ {\mathit{\boldsymbol{K/}}\left\{ {\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right)} \right\}} \right\}} \right)} \end{array} $
(13) $ \begin{array}{*{20}{c}} {{d_4}\left( {{x_4},{y_4}} \right) = \left( {f \otimes \mathit{\boldsymbol{K}}} \right)\left( {{x_4},{y_4}} \right) = }\\ {\arg \_\max \left\{ {{D_{\rm{m}}}\left( {f\left( {{x_4} + s,{y_4} + t} \right),\mathit{\boldsymbol{K}}} \right)} \right\},}\\ {\left( {\left( {s,t} \right) \in \left\{ {\mathit{\boldsymbol{K/}}\left\{ {\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right)} \right\}} \right\}} \right)} \end{array} $
(14) 式中，Dm的定义如(7)式所示，(12)式中K/{(x1, y1)}表示集合K与集合{(x1, y1)}的差集。
用改进的结构元素对高光谱图像进行膨胀操作的示意图如图 3所示。大小为4×4的结构元素内包含A和C两种纯净像元，以及由它们混合而成的混合像元B，分别根据(11)式~(14)式计算出该结构元素内纯净度最大的4个像元d1, d2, d3, d4，并用它们取代像元P1, P2, P3以及P4。可以看出，利用改进的结构元素进行膨胀操作时，纯净像元A和C都被保留了下来，有效避免了可能的信息丢失。
Figure 3. Diagram of dilation operation with the improved structure element
-
上面已经对自动形态学端元提取算法的缺陷进行了说明，并对其中一些不足之处进行了改进。分别将改进的形态学算子、改进的MEI计算方法以及改进的结构元素依次引入到自动形态学端元提取算法中，将得到的改进方法依次命名为M-AMEE1, M-AMEE2和M-AMEE3。
以上3种方法是从不同角度对AMEE算法进行改进得到的，它们相对于原始算法都有不同程度的提升，然而其中任何一个改进算法与其它两个相比都存在不足之处。为此，提出一种从以上3个方面同时改进的基于自动形态学的端元提取算法，命名为M-AMEE4。具体步骤如下：(1)输入高光谱图像数据X∈Rl×n，采用虚拟维度法(virtual dimensionality，VD)[14]估计图像中的端元数p；(2)设置结构元素Kmin, Kmax，其中Kmin和Kmax中的元素数量均为偶数，则可以求得最大迭代次数Imax，计算图像的参考光谱向量Uben；(3)初始化：假设i=1，每一个像元f(x, y)的IMEI, m(x, y)=0；(4)将结构元素K在图像中移动，按照改进的膨胀操作，得到结构元素内纯度最高的4个像元；(5)根据(10)式更新改进的MEI值；(6)i=i+1，如果i=Imax，执行步骤(7), 否则，将原始图像f用(f$ \otimes $K)代替，增大结构元素K，然后执行步骤(4), 其中(f$ \otimes $K)表示改进的膨胀操作；(7)输出MEI图像，改进的MEI值大于特定阈值的像元组成候选端元集；(8)从候选端元集中选取形态学离心率指数最大的像元作为图像的第1个端元e1，设置已获取端元数n=1；(9)当n＞1时，从候选端元集中选取与已知端元组成的单形体的体积最大的像元作为下一个端元；(10)如果n＜p，则n→n+1转到第(9)步继续迭代，否则停止迭代得到p个端元(e1, e2, …, ep)。
-
实验中用的高光谱数据来自美国内华达州Cuprite地区，由机载可见光/红外光谱成像仪(airborne visible/infrared imaging spectrometer，AVIRIS)获取。Cuprite地区地表多为裸露矿物，目前已经确定的矿物多达数十种[15]。本文中采用该数据中的短波红外部分(波长1990nm~2479nm)，图像大小为350×400个像元，包含50个波段，由ENVI软件提供。
利用AMEE和4种改进的算法对上述高光谱数据进行端元提取实验。对于AMEE，M-AMEE1和M-AMEE2算法，设置最小和最大结构元素分别为3×3, 11×11，M-AMEE3和M-AMEE4算法中最小和最大结构元素分别为4×4和12×12。用光谱夹角距离来定量比较提取到的端元与实际地物之间的相似性，其中实际端元数据从美国地质勘探局(United States Geological Survey，USGS)网站获得，结果见表 1。
Table 1. Comparison on endmember extraction result of Cuprite data
algorithm spectral angle distance in radian alunite buddingtonite calcite kaolinite muscovite average AMEE 0.0954 0.1354 0.1124 0.1219 0.1368 0.1204 M-AMEE1 0.0954 0.1268 0.1124 0.0937 0.1334 0.1123 M-AMEE2 0.0954 0.1354 0.1029 0.0886 0.1180 0.1081 M-AMEE3 0.0954 0.1268 0.0927 0.1163 0.1368 0.1136 M-AMEE4 0.0954 0.1268 0.0927 0.0752 0.1104 0.1001 由表 1可以看出，M-AMEE1, M-AMEE2和M-AMEE3这3种改进算法端元提取的精度相对于原始方法都有一定程度的提高，而M-AMEE4算法由于同时具备上述3种算法的优点，因而其端元提取的效果最好。因此，下面重点对M-AMEE4算法进行研究。
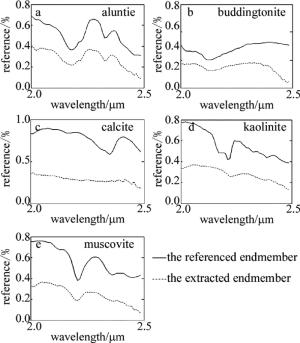
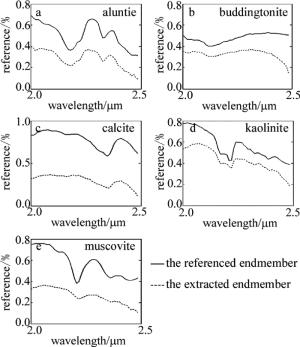
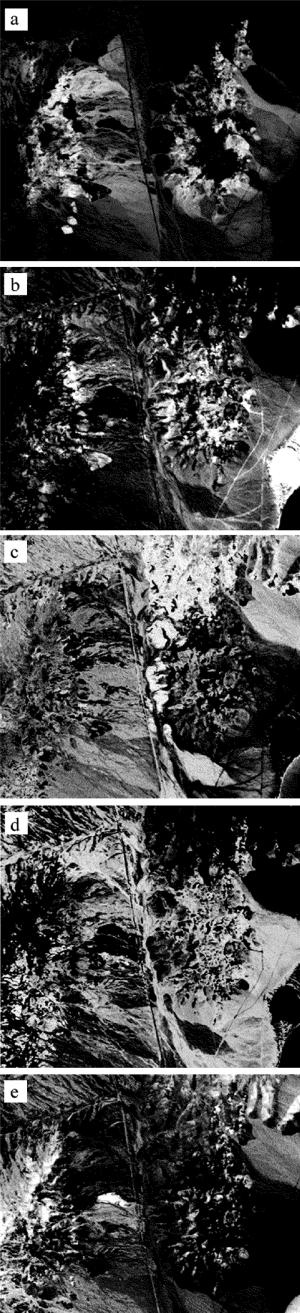
图 4和图 5分别给出了用AMEE和M-AMEE4算法提取到的该地区常见的5种矿物的光谱曲线以及参考光谱曲线的对比图。图中实线表示参考光谱曲线，上述两种算法提取的端元曲线用虚线表示。
Figure 4. Comparison between the endmembers extracted by AMEE and the referenced endmembers
Figure 5. Comparison between the endmembers extracted by M-AMEE4 and the referenced endmembers
从以上图中可以看出，用AMEE和M-AMEE4两种算法提取的矿物曲线与参考光谱曲线有不同程度的吻合。将上述两种算法提取到的像元作为图像的端元，用全约束最小二乘法进行丰度反演，得到各个地物的分布图, 如图 6和图 7所示。将得到的地物分布图与USGS公布的Cuprite地区矿物分布图进行对比，可以比较出各算法端元提取的效果。
Figure 6. Abundance maps of endmembers extracted by AMEE
Figure 7. Abundance maps of endmembers extracted by M-AMEE4
-
本文中对AMEE算法存在的一些缺陷进行了分析与研究，并提出了几种改进方法。针对AMEE算法中定义的形态学算子在纯像元集中分布的区域无法得到正确结果的问题，通过引入参考光谱向量构建了改进的形态学算子，并给出了改进的MEI计算方法。对于AMEE算法中在每个结构元素内只提取一个候选端元容易造成重要像元丢失的缺陷，通过引入偶数大小的结构元素定义了改进的结构元素。分别利用改进的形态学算子、改进的MEI计算方法以及改进的结构元素对自动形态学端元提取算法进行分析，得到3种改进的算法:M-AMEE1, M-AMEE2和M-AMEE3，而将从以上3个方面同时改进的基于自动形态学的端元提取算法命名为M-AMEE4。将改进的算法应用于实际高光谱数据，发现M-AMEE1，M-AMEE2和M-AMEE3端元提取的精度相对于原始方法都有一定程度的提高，而M-AMEE4算法由于同时具备上述3种算法的优点，端元提取的效果最好。从最终的结果来看，M-AMEE4算法端元提取的精度和像元解混的效果都要优于AMEE，证明了改进算法的有效性。
一种改进的基于自动形态学的端元提取算法
An improved endmember extraction algorithm based on automated morphology
-
摘要: 自动形态学端元提取（AMEE）算法中的形态学算子在纯像元集中分布的区域无法得到正确的结果。现有膨胀操作在每个结构元素内只能提取一个候选端元，会造成重要像元丢失。为了解决这些问题，采用改进的形态学算子和结构元素对AMEE算法进行了改进。首先引入参考光谱向量的概念构建了改进的形态学算子，并给出了形态学离心率指数新的计算方法，然后利用偶数大小、改进的结构元素，从每个结构元素内选出4个候选端元，最后对改进的基于自动形态学的端元提取算法进行了分析和实验验证。结果表明，改进的方法能从纯像元集中分布的区域获得正确的候选端元，并在一定程度上避免膨胀过程中的信息遗失，从而能够有效地提升端元提取的精度和像元解混的效果。Abstract: Morphological operators used in the automated morphological endmember extraction (AMEE) algorithm didn't acquire correct result in the area of pure pixel concentration distribution. The dilation operation only chose one candidate endmember from each structure element and would lose some important pixels. In order to solve the problem, the AMEE algorithm was modified by an improved morphological operator and new structural element. The improved morphological operator was proposed after introducing the concept of reference spectral vector, and a new calculation method of morphological eccentricity index was given. To avoid information loss, four candidate endmembers were chosen from each improved even-numbered structure element. The modified automated morphological endmember extraction algorithm was tested based on a hyperspectral data set. The experimental results show that the improved method can obtain correct candidate endmembers from the area of pure pixel concentration distribution, and information loss in the procedure of dilation is also avoided. The proposed method produces more accurate results of endmember extraction and the spectral unmixing.
-
Key words:
- remote sensing /
- hyperspectral image /
- endmember extraction /
- morphology
-
Figure 1. Comparison on dilation results of simulation image
a—original image b—dilation result c—the improved dilation result
Figure 4. Comparison between the endmembers extracted by AMEE and the referenced endmembers
Figure 5. Comparison between the endmembers extracted by M-AMEE4 and the referenced endmembers
Figure 6. Abundance maps of endmembers extracted by AMEE
a—alunite b—buddingtonite c—calcite d—kaolinite e—muscovite
Figure 7. Abundance maps of endmembers extracted by M-AMEE4
a—alunite b—buddingtonite c—calcite d—kaolinite e—muscovite
Table 1. Comparison on endmember extraction result of Cuprite data
algorithm spectral angle distance in radian alunite buddingtonite calcite kaolinite muscovite average AMEE 0.0954 0.1354 0.1124 0.1219 0.1368 0.1204 M-AMEE1 0.0954 0.1268 0.1124 0.0937 0.1334 0.1123 M-AMEE2 0.0954 0.1354 0.1029 0.0886 0.1180 0.1081 M-AMEE3 0.0954 0.1268 0.0927 0.1163 0.1368 0.1136 M-AMEE4 0.0954 0.1268 0.0927 0.0752 0.1104 0.1001 
下载: 导出CSV
-
[1] WANG K, QU H M. Anomaly detection method based on improved minimum noise fraction transformation[J]. Laser Technology, 2015, 39(3):381-385(in Chinese). [2] KONG X B, SHU N, GONG Y, et al. Integration of spatial-spectral information based endmember extraction for hyperspectral image[J]. Spectroscopy and Spectral Analysis, 2013, 33(6):1647-1652(in Chinese). [3] YANG J. Unmixing pixels in hyperspectral/multispectral image[D]. Wuhan: Huazhong University of Science & Technology, 2011: 8-10(in Chinese). [4] BOARDMAN J W, KRUSE F A, GREEN R O. Mapping target signatures via partial unmixing of AVIRIS data[C]//NASA Summaries of the Fifth Annual JPL Airborne Earth Science Workshop. Washington DC, USA: NASA, 1995: 23-26. [5] WINTER E M. N-FINDER:an algorithm for fast autonomous spectral endmember determination in hyperspectral data[J]. Proceedings of the SPIE, 1999, 3753:266-275. doi: 10.1117/12.366289 [6] CHANG Ch N, WU Ch Ch, LIU W M, et al. A new growing method for simplex-based endmember extraction algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(10):2804-2819. doi: 10.1109/TGRS.2006.881803 [7] NEVILLE R A, STAENZ K, SZEREDI T, et al. Automatic endmember extraction from hyperspectral data for mineral exploration[J]. Proceedings of the Canadian Symposium on Remote Sensing, 1999(6):21-24. [8] XU H. The new method for decomposition of mixed pixels in remote sensing images and its applications research[D]. Beijing: Capital Normal University, 2013: 28-32(in Chinese). [9] PLAZA A, MARTINEZ P, PEREZ R, et al. Spatial/spectral endmember extraction by multidimensional morphological operations[J]. IEEE Geoscience and Remote Sensing, 2002, 40(9):2025-2041. doi: 10.1109/TGRS.2002.802494 [10] WU H. The research of endmember extraction from hyperspectral image based on mathematic morphology[D]. Chengdu: Chengdu University of Technology, 2011: 32-37(in Chinese). [11] OTSU N. A threshold selection method from gray-level histogram[J]. IEEE Transactions on Systems, Man and Cybernetics, 1979, 9(1):62-66. doi: 10.1109/TSMC.1979.4310076 [12] WANG Y, LIANG N, GUO L. A hyperspectral remote sensing image endmember exraction algorithm based on modified exrended-morphological operator[J]. Acta Photonica Sinica, 2012, 41(6):672-677(in Chinese). doi: 10.3788/gzxb [13] WU B, ZHANG L P, LI P X. Unsupervised orthogonal subspace projection approach to unmix hyperspectral imagery automatically[J]. Journal of Image and Graphics, 2004, 9(11):1392-1396(in Chinese). [14] CHANG Ch N, DU Q. Estimation of number of spectrally distinct signal sources in hyperspectral imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(3):608-619. doi: 10.1109/TGRS.2003.819189 [15] WANG M Zh. Researches on several critical problems of hyperspectral remote sensing image processing and geologic application[D]. Chengdu: Chengdu University of Technology, 2014: 41-48(in Chinese). -
点击查看大图
图(7) / 表(1)
计量
- 文章访问数: 6870
- HTML全文浏览量: 4912
- PDF下载量: 244
- 被引次数: 0
