网站地图
-
椭偏仪是研究与分析薄膜材料表面特性的重要工具[1]。由于没有转动部件，斯托克斯椭偏仪[2]能够实时或快速测量薄膜等材料的光学参量[3-4]，从而可以监控薄膜生长过程、细胞的动态光学性质，以及检测材料受到外界作用时瞬时特性改变[5-7]。斯托克斯椭偏仪的核心部件是振幅分割光偏振态测量模块(division-of-amplitude photopolarimeter, DOAP)[8-9]。1982年，AZZAM设计了第1台基于振幅分割的光偏振态测量仪[10]。随后，出现了各种结构的DOAP[11-14]。研究表明：DOAP系统存在最优的仪器矩阵，它对组成系统的分光器件参量有严格的镀膜及加工要求[15-16]。这给制作满足特定要求的分光器件工艺带来困难。如果分光器件不满足特定的要求，则系统的仪器矩阵有可能是一个奇异矩阵，从而使测量精度降低，甚至使测量结果出现严重偏差。本文中在传统DOAP[10]的分光棱镜与沃拉斯顿棱镜之间的光路上插入波片，通过波片对光的偏振态调制作用[17]实现仪器矩阵的优化。作者推导出改进后系统的仪器矩阵，详细分析了波片参量及方位角对仪器矩阵条件数大小的影响，得到了两块波片的最佳方位角和最佳相位延迟量满足的关系，从而进一步提高了斯托克斯椭偏仪的测量准确度及稳定性。实验结果表明：通过调节波片的相位延迟量或方位角可以优化系统仪器矩阵。优化后的斯托克斯椭偏仪测量薄膜样品的厚度和折射率的标准差分别为0.1nm和0.001。
-
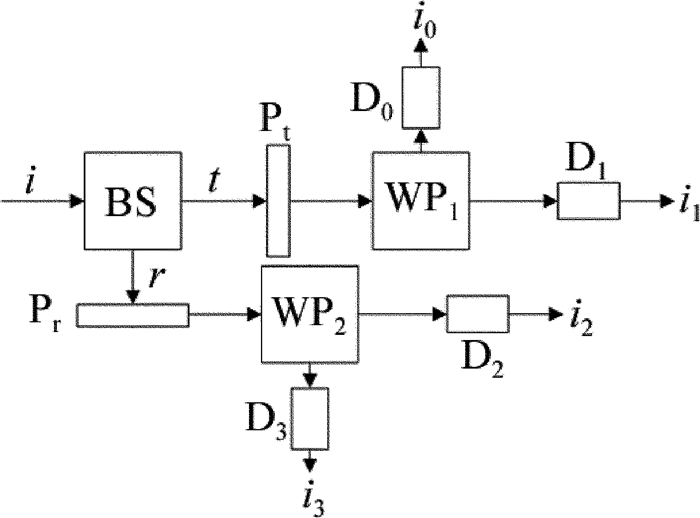
反射式斯托克斯椭偏仪采用DOAP结构作为光偏振态斯托克斯参量测量模块。其测量光偏振态的方程为：I=X·S，其中I为测量到的4路电流信号的4×1矩阵，S为待测光偏振态的4个斯托克斯参量的4×1矩阵，X为4×4的仪器矩阵，它的质量好坏直接影响光偏振态斯托克斯参量的测量精度，间接限制椭偏仪的测量精确度。为了实现仪器矩阵的优化，在传统DOAP的分光棱镜后的透射及反射光路上分别引进一块波片。改进后的DOAP光路结构如图 1所示。图 1中，i表示入射光, t和r分别表示透射光和反射光，BS为分光棱镜，Pt和Pr分别表示透射和反射光路的波片，WP1和WP2分别表示透射和反射光路的沃拉斯顿棱镜，D0, D1, D2和D3是同一种型号的光电探测器，i0, i1, i2和i3是光电探测器经过光电转换后的电信号。
Figure 1. Structure of the improved DOAP
令T和R分别表示分光棱镜透射和反射的米勒矩阵，用Mt和Mr分别表示透射和反射光路中波片的米勒矩阵，W代表沃拉斯顿棱镜米勒矩阵的第1行，α1和α2分别是透射和反射光路中沃拉斯顿棱镜方位角，则测量系统的仪器矩阵的表达式X为:
$ \mathit{\boldsymbol{X = }}\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{W}}({\alpha _1}){\mathit{\boldsymbol{M}}_{\rm{t}}}\mathit{\boldsymbol{T}}\\ \mathit{\boldsymbol{W}}({\alpha _1} + \frac{{\rm{ \mathsf{ π} }}}{2}){\mathit{\boldsymbol{M}}_{\rm{t}}}\mathit{\boldsymbol{T}}\\ \mathit{\boldsymbol{W}}({\alpha _2}){\mathit{\boldsymbol{M}}_{\rm{r}}}\mathit{\boldsymbol{R}}\\ \mathit{\boldsymbol{W}}({\alpha _2} + \frac{{\rm{ \mathsf{ π} }}}{2}){\mathit{\boldsymbol{M}}_{\rm{r}}}\mathit{\boldsymbol{R}} \end{array}} \right] $
(1) 以(1)式的第1行为例分析。设分光棱镜的透射椭偏参量为ψt和δt，则分光棱镜透射光路的米勒矩阵T为：
$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{T}} = {t_0} \times }\\ {\left[ {\begin{array}{*{20}{c}} 1&{ - \cos \left( {2{\psi _t}} \right)}&0&0\\ { - \cos \left( {2{\psi _t}} \right)}&1&0&0\\ 0&0&{\sin \left( {2{\psi _t}} \right)\cos {\delta _{\rm{t}}}}&{\sin \left( {2{\psi _t}} \right)\sin {\delta _{\rm{t}}}}\\ 0&0&{ - \sin \left( {2{\psi _t}} \right)\sin {\delta _{\rm{t}}}}&{\sin \left( {2{\psi _t}} \right)\cos {\delta _{\rm{t}}}} \end{array}} \right]} \end{array} $
(2) 式中，t0为分光棱镜的透射系数。令A1=-cos(2ψt), B1=sin(2ψt)cosδt, C1=sin(2ψt)sinδt，则T可以简化为：
$ \mathit{\boldsymbol{T}} = {t_0}\left[ {\begin{array}{*{20}{c}} 1&{{A_1}}&0&0\\ {{A_1}}&1&0&0\\ 0&0&{{B_1}}&{{C_1}}\\ 0&0&{ - {C_1}}&{{B_1}} \end{array}} \right] $
(3) 令βt和Φt分别为透射光路波片的偏振方位角和相位延迟量，则透射光路上的波片的传输矩阵Mt为：
$ \begin{array}{l} {\mathit{\boldsymbol{M}}_{\rm{t}}} = \\ \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&{{{\cos }^2}\left( {2{\beta _t}} \right) + {{\sin }^2}\left( {2{\beta _t}} \right)\cos {\mathit{\Phi }_{\rm{t}}}}&{\left( {1 - \cos {\mathit{\Phi }_{\rm{t}}}} \right)\sin \left( {2{\beta _t}} \right)\cos \left( {2{\beta _t}} \right)}&{ - \sin \left( {2{\beta _t}} \right)\sin {\mathit{\Phi }_{\rm{t}}}}\\ 0&{\left( {1 - \cos {\mathit{\Phi }_{\rm{t}}}} \right)\sin \left( {2{\beta _t}} \right)\cos \left( {2{\beta _t}} \right)}&{{{\sin }^2}\left( {2{\beta _t}} \right) + {{\cos }^2}\left( {2{\beta _t}} \right)\cos {\mathit{\Phi }_{\rm{t}}}}&{\cos \left( {2{\beta _t}} \right)\sin {\mathit{\Phi }_{\rm{t}}}}\\ 0&{\sin \left( {2{\beta _t}} \right)\sin {\mathit{\Phi }_{\rm{t}}}}&{ - \cos \left( {2{\beta _t}} \right)\sin {\mathit{\Phi }_{\rm{t}}}}&{\cos {\mathit{\Phi }_{\rm{t}}}} \end{array}} \right] \end{array} $
(4) 为了方便分析，设α1与α2为45°，此时沃拉斯顿棱镜的米勒矩阵第1行为：
$ \mathit{\boldsymbol{W}}\left( {45{\rm{^\circ }}} \right) = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} 1&0&1&0 \end{array}} \right] $
(5) 把(3)式、(4)式和(5)式代入(1)式, 可算得(1)式第1行的结果为：
$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_1} = \frac{1}{2} \times }\\ {{{\left[ {\begin{array}{*{20}{c}} {{t_0}\left[ {1 + {A_1}\left( {1 - \cos {\mathit{\Phi }_{\rm{t}}}} \right)\sin \left( {2{\beta _t}} \right)\cos \left( {2{\beta _t}} \right)} \right]}\\ {{t_0}\left[ {{A_1}\left( {1 - \cos {\mathit{\Phi }_{\rm{t}}}} \right)\sin \left( {2{\beta _t}} \right)\cos \left( {2{\beta _t}} \right)} \right]}\\ {{t_0}{B_1}\left[ {{{\sin }^2}\left( {2{\beta _t}} \right) + {{\cos }^2}\left( {2{\beta _t}} \right)\cos {\mathit{\Phi }_{\rm{t}}}} \right] - {t_0}{C_1}\cos \left( {2{\beta _t}} \right)\sin {\mathit{\Phi }_{\rm{t}}}}\\ {{t_0}{C_1}\left[ {{{\sin }^2}\left( {2{\beta _t}} \right) + {{\cos }^2}\left( {2{\beta _t}} \right)\cos {\mathit{\Phi }_{\rm{t}}}} \right] + {t_0}{B_1}\cos \left( {2{\beta _t}} \right)\sin {\mathit{\Phi }_{\rm{t}}}} \end{array}} \right]}^{\rm{T}}}} \end{array} $
(6) 式中，T是矩阵的转置。同理可算出系统的仪器矩阵X的其它行。计算得到优化后DOAP的仪器矩阵X为：
$ \begin{array}{l} \mathit{\boldsymbol{X = }}\frac{1}{2}\\ \left[ {\begin{array}{*{20}{c}} {{t_0}\left[ {1 + {A_1}{D_1}\left( {1 - \cos {\mathit{\Phi }_{\rm{t}}}} \right)} \right]}&{{t_0}\left[ {{A_1} + {D_1}\left( {1 - \cos {\mathit{\Phi }_{\rm{t}}}} \right)} \right]}&{{t_0}\left( {{B_1}{E_1} - {C_1}{F_1}} \right)}&{{t_0}\left( {{C_1}{E_1} + {B_1}{F_1}} \right)}\\ {{t_0}\left[ {1 - {A_1}{D_1}\left( {1 - \cos {\mathit{\Phi }_{\rm{t}}}} \right)} \right]}&{{t_0}\left[ {{A_1} - {D_1}\left( {1 - \cos {\mathit{\Phi }_{\rm{t}}}} \right)} \right]}&{{t_0}\left( {{C_1}{F_1} - {B_1}{E_1}} \right)}&{ - {t_0}\left( {{C_1}{E_1} + {B_1}{F_1}} \right)}\\ {{r_0}\left[ {1 + {A_2}{D_2}\left( {1 - \cos {\mathit{\Phi }_{\rm{r}}}} \right)} \right]}&{{r_0}\left[ {{A_2} + {D_2}\left( {1 - \cos {\mathit{\Phi }_{\rm{r}}}} \right)} \right]}&{{r_0}\left( {{B_2}{E_2} - {C_2}{F_2}} \right)}&{{r_0}\left( {{C_2}{E_2} + {B_2}{F_2}} \right)}\\ {{r_0}\left[ {1 + {A_2}{D_2}\left( {1 - \cos {\mathit{\Phi }_{\rm{r}}}} \right)} \right]}&{{r_0}\left[ {{A_2} - {D_2}\left( {1 - \cos {\mathit{\Phi }_{\rm{r}}}} \right)} \right]}&{{r_0}\left( {{C_2}{F_2} - {B_2}{E_2}} \right)}&{ - {r_0}\left( {{C_2}{E_2} + {B_2}{F_2}} \right)} \end{array}} \right] \end{array} $
(7) 式中，r0是分光棱镜的反射系数，A2=-cos(2ψr), B2=sin(2ψr)cosδr, C2=sin(2ψr)sinδr, D1=sin(2βt)×cos(2βt), D2=sin(2βr)cos(2βr), E1=sin2(2βt)+cos2(2βt)cosΦt, E2=sin2(2βr)+cos2(2βr)cosΦr, F1=cos(2βt)sinΦt, F2=cos(2βr)sinΦr。其中，ψr和δr分别是分光棱镜的反射椭偏参量，βr和Φr分别为反射光路上波片的偏振方位角和相位延迟量。当Φt=Φr=0°时，(7)式对应于参考文献[15]中未加波片时的仪器矩阵，是一种特例。
由(7)式可知，仪器矩阵与波片的方位角和相位延迟量有关，这为利用波片优化系统仪器矩阵提供了依据。
-
矩阵条件数是判断矩阵病态与否的一种度量，条件数越大则矩阵越病态。对于椭偏测量系统，仪器矩阵的条件数反映了测量误差及系统抵抗噪声的能力。条件数越小，则测量系统越稳定，测量结果越可靠。由(7)式可知，通过调整DOAP中波片的方位角(βt, βr)和相位延迟量(Φt, Φr)，可以实现系统仪器矩阵的优化，提高椭偏仪的测量稳定性。可以讨论两种情况下仪器矩阵条件数与波片参量的关系：(1)固定波片的方位角，分析相位延迟量与仪器矩阵条件数的关系；(2)固定波片的相位延迟量，分析方位角与仪器矩阵条件数的关系。
显然，后一种思路更具有实用意义。而从理论分析可知，这两种情况得到的最佳波片参量应该相一致，因此下面仅分析第2种情况。给定波片的相位延迟量，此时在仪器矩阵中的变量只有波片的方位角。以常见的波片λ/2波片和λ/4波片为例，在透射和反射光路中各插入一块波片，共有4种情形。以某型号的普通分光棱镜为例，其透射系数t0与反射系数r0均为0.5；用椭偏仪实测其透射椭偏参量为ψt=66.27°和δt=6.825°; 反射椭偏参量为ψr=21.04°和δr=188.19°。这时，波片方位角(βt, βr)与仪器矩阵条件数的关系如图 2所示，色条值表示条件数的大小。
Figure 2. Relationships between condition number and azimuthal angle of waveplates
由图 2a、图 2b和图 2c可知，当波片的方位角(βt, βr)取0°，45°，90°和135°的离散组合时，系统仪器矩阵的条件数最小，此时的波片的方位角(βt, βr)为最佳方位角组合，具有周期性。由图 2a可知，最佳方位角组合满足线性方程关系βt=βr±45°或βt=βr±135°；由图 2b可知，最佳方位角组合满足线性方程关系βt=0°, βt=90°；由图 2c可知，最佳方位角组合满足线性方程关系βr=0°, βr=90°。值得注意的是，由图 2d可知，当反射与透射光路均插入λ/2波片时，仪器矩阵的条件数最小值都大于100，很难实现仪器矩阵的优化。
-
为了更方便及实用地实现仪器矩阵的优化，使DOAP系统更加简单。下面将探讨仅在透射光路或者反射光路放置波片对仪器矩阵条件数的影响。
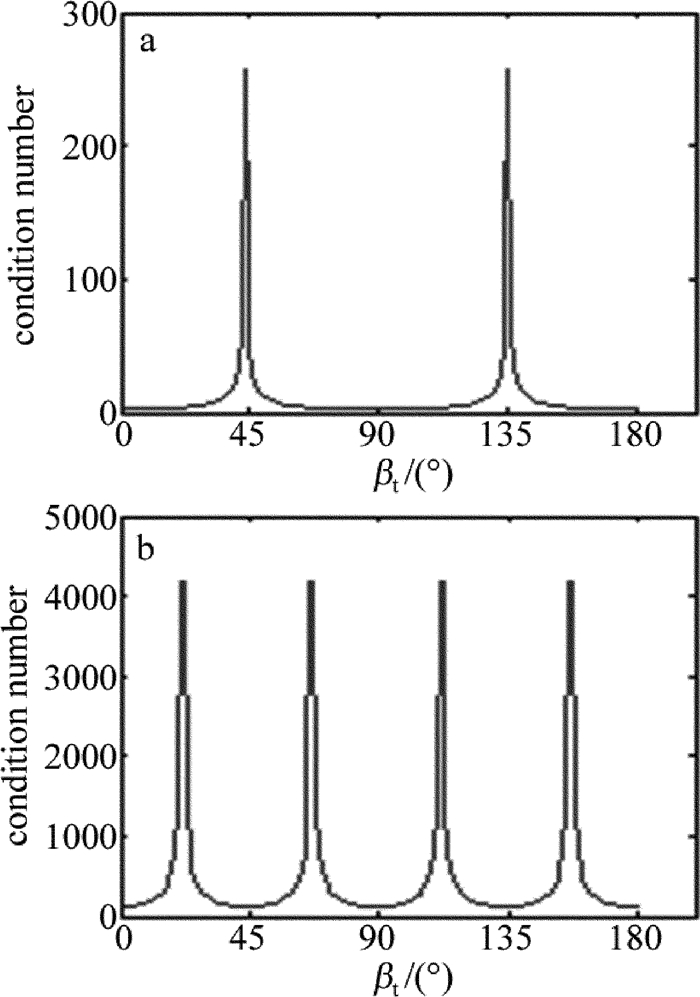
仅在透射光路中插入一块相位延迟量为Φt的波片，而反射光路中没有波片，相应于相位延迟量Φr=0°。此时，仪器矩阵的条件数大小取决于透射光路波片的相位延迟量Φt和方位角βt。图 3为固定相位延迟量为Φt=90°和Φt=180°时仪器矩阵条件数与波片方位角的关系。
Figure 3. Relationships between condition number and azimuthal angle of waveplates when one waveplate was inserted in transmition light path
由图 3可知，仅透射光路放入波片时，仪器矩阵条件数大小与波片方位角满足一定的周期关系。仅放入λ/4波片时，条件数的最小值可接近于0，这时对应的波片方位角在0°，90°及180°附近，可以实现仪器矩阵的最优化，避免波片方位角处于45°及135°；仅放入λ/2波片，条件数的最小值也大于100，不适合于优化仪器矩阵。因此，放入λ/4波片效果最佳。仅在反射光路放入波片时，可得到与图 3相似的结果。
-
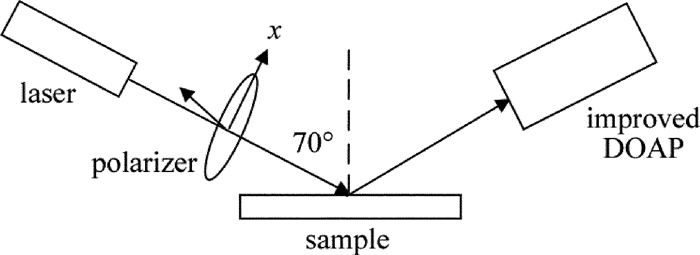
为了验证优化DOAP系统后的测量准确度及重复性精度，组建了相应的斯托克斯椭偏仪测量系统，如图 4所示，选择仅在DOAP的透射光路插进一块λ/4波片。从He-Ne激光器出射的632.0nm激光束通过方位角为45°或135°的偏振片后以70°入射角入射到薄膜样品，反射后的偏振光进入优化后的DOAP。4路输出电流信号被放大后由计算机采样。选择4块标准薄膜样品，采用在位四区定标方法测量系统的仪器矩阵[18-19]并计算其条件数。表 1是插入一块λ/4波片前后测量3块不同条件镀制的硅衬底表面SiO2薄膜的实验结果。采用定标过的美国L116S300型STOKES椭偏仪测量结果作为参考值或标准值。分析表 1可知：(1)条件数越小，测量薄膜厚度及折射率的精确度越高；(2)系统插入波片，调节其方位角为90°时，测量系统处于最佳状态，测量薄膜厚度及折射率的重复性精度分别达到0.1nm和0.001。通过插入波片，可以实现椭偏测量系统的优化。这些结论与理论分析完全一致(见图 3a)。
Figure 4. Stokes ellipsometer with the optimized DOAP
Table 1. Measurement results of Stokes ellipsometer before and after the insert of wave-plate
no wave-plate quarter wave-plate at 45° quarter wave-plate at 90° reference value condition number 156.53 171.08 32.63 — sample 1 thickness/nm 95.3±0.9 95.1±0.9 102.1±0.1 101.84±0.04 refractive index 1.550±0.006 1.528±0.009 1.454±0.001 1.460±0.001 sample 2 thickness/nm 144.7±0.9 142.8±0.9 162.9±0.1 162.03±0.05 refractive index 1.565±0.007 1.571±0.011 1.460±0.001 1.463±0.001 sample 3 thickness/nm 109.0±1.1 113.2±1.2 184.9±0.1 185.19±0.04 refractive index 1.931±0.009 1.775±0.014 1.455±0.001 1.454±0.001 -
通过选择合适的波片，改进了传统的DOAP系统，保证了斯托克斯光偏振态分振幅测量模块的测量稳定性及准确度。分析与实验表明：以条件数为判据，仪器矩阵存在最佳的波片参量，通过选择波片的最佳方位角或位相延迟量可以实现仪器矩阵的优化，从而提高斯托克斯椭偏仪的测量精确度。特别地，如选择λ/4波片，测量系统的优化更有效、方便及简单，在光偏振态测量领域具有较大的实用价值。
斯托克斯光偏振态测量系统的优化
Optimization of Stokes optical polarization measurement system
-
摘要: 为了满足光偏振态分振幅测量模块（DOAP）对分光棱镜复杂且严格的加工要求，采用在经典DOAP透射光路及反射光路各引入一块波片的方法，组成改进后的光偏振态测量模块。推导了新的仪器矩阵表达式，通过分析波片参量对仪器矩阵条件数的影响，得到了最佳波片的参量及其关系。结果表明，优化后的斯托克斯椭偏仪测量薄膜样品的厚度和折射率的标准差分别为0.1nm和0.001。通过选择波片的最佳方位角或相位延迟量可以实现斯托克斯椭偏仪仪器矩阵的优化，从而提高系统的测量稳定性及可靠性。Abstract: Division-of-amplitude photopolarimeter(DOAP) was the key part of Stokes ellipsometer. To reach the complex and strict processing demands of beam splitter in DOAP, two waveplates are inserted respectively in the reflection light path and transmittion light path of classic DOAP to form an improved DOAP. The instrument matrix of new DOAP was derived and influence of waveplate parameters on the condition number of instrument matrix was also analyzed. From theoretical analysis and experimental verification, the optimal parameters and their relationships of waveplates were gotten. The results show that, measurement standard errors of film thickness and refractive index of the optimized Stokes ellipsometer are 0.1nm and 0.001 respectively. By choosing the optimal azimuthal angles or phase retardations of waveplates, the instrument matrix can be optimized to improve the accuracy and stability of measurement.
-
Figure 2. Relationships between condition number and azimuthal angle of waveplates
a—Φt=90°, Φr=90° b—Φt=90°, Φr=180° c—Φt=180°, Φr=90° d—Φt=180°, Φr=180°
Figure 3. Relationships between condition number and azimuthal angle of waveplates when one waveplate was inserted in transmition light path
a—Φt=90° b—Φt=180°
Table 1. Measurement results of Stokes ellipsometer before and after the insert of wave-plate
no wave-plate quarter wave-plate at 45° quarter wave-plate at 90° reference value condition number 156.53 171.08 32.63 — sample 1 thickness/nm 95.3±0.9 95.1±0.9 102.1±0.1 101.84±0.04 refractive index 1.550±0.006 1.528±0.009 1.454±0.001 1.460±0.001 sample 2 thickness/nm 144.7±0.9 142.8±0.9 162.9±0.1 162.03±0.05 refractive index 1.565±0.007 1.571±0.011 1.460±0.001 1.463±0.001 sample 3 thickness/nm 109.0±1.1 113.2±1.2 184.9±0.1 185.19±0.04 refractive index 1.931±0.009 1.775±0.014 1.455±0.001 1.454±0.001 
下载: 导出CSV
-
[1] XIAO G H, HUANG Z H, LIU Ch N, et al. Analysis of ellipsometric data processing about transparent film on the transparent substrate[J]. Laser Technology, 2010, 34(2):247-249(in Chinese). [2] CHENG M X, HE Zh J, HUANG Z H. A method of ellipsometry based on Stokes parameters with a division-of-amplitude polarimeter(DOAP) system[J]. Opto-Electronic Engineering, 2009, 36(7):100-106(in Chinese). [3] LÜ X, JIANG Zh Q, LI Y Ch. Study on the measurement of SOP with high-speed and real-time[J]. Optical Technique, 2010, 36(6):866-870(in Chinese). [4] QIN Z Y, CHENG Z G, ZHANG Z P, et al. High-speed and real-time measurement of Stokes parameters[J]. Acta Optica Sinica, 2007, 27(4):659-662(in Chinese). [5] LIN H H, PHAN Q H, LO Y L. Characterization of voltage-driven twisted nematic liquid crystal cell by dynamic polarization scanning ellipsometry[J]. Optics Express, 2015, 23(8):10213-10223. doi: 10.1364/OE.23.010213 [6] HALL S A, COVERT P A, BLINN B R, et al. Rapid and sensitive polarization measurement for characterizing protein adsorption at the solid-liquid interface[J]. Journal of Physical Chemistry, 2013, C117(4):1796-1803. [7] LO Y L, HSIEH W H, CHUNG Y F, et al. An approach for measuring the ellipsometric parameters of isotropic and anisotropic thin films using the stokes parameter method[J]. Journal of Lightwave Technology, 2012, 30(14):2299-2306. doi: 10.1109/JLT.2012.2196977 [8] CHENG M X, HE Z J, HUANG Z H. Measurement and application of stokes parameters of polarized light[J]. Infrared and Laser Engineering, 2006, 35(s2):109-115(in Chinese). [9] XU X S. The design of an experimental study of polarimeter system of Stokes parameters based on division-of-amplitude[D]. Hangzhou: Zhejiang University, 2011: 44-52(in Chinese). [10] AZZAM R M A. Division-of-amplitude photopolarimeter (DOAP) for the simultaneous measurement of all four Stokes parameters of light[J]. Optica Acta, 1982, 29(5):685-689. doi: 10.1080/713820903 [11] AZZAM R M A. Division-of-amplitude photopolarimeter based on conical diffraction from a metallic grating[J]. Applied Optics, 1992, 31(19):3574-3576. doi: 10.1364/AO.31.003574 [12] AZZAM R M A, SUDRADJAT F F. Single-layer-coated beam splitters for the division-of-amplitude photopolarimeter[J]. Applied Optics, 2005, 44(2):190-196. doi: 10.1364/AO.44.000190 [13] TAYA S A, EI-AGEZ T M, ALKANOO A A. Ellipsometric configurations using a phase retarder and a rotating polarizer and analyzer at any speed ratio[J]. Chinese Physics, 2012, B21(11):110701. [14] YUAN W J, SHEN W D, ZHANG Y G, et al. Dielectric multilayer beam splitter with differential phase shift on transmission and reflection for division-of-amplitude photopolarimeter[J]. Optics Express, 2014, 22(9):11011-11020. doi: 10.1364/OE.22.011011 [15] AZZAM R M A. Beam splitters for the division-of-amplitude photopolarimeter[J]. Optica Acta, 1985, 32(11):1407-1412. doi: 10.1080/713821665 [16] AZZAM R M A. Optimal beam splitters for the division-of-amplitude photopolarimeter[J]. Journal of the Optical Society of America, 2003, A20(5):955-958. [17] REN Sh F, WANG X X. Polarization states of linearly polarized light transmitting through several wave-plates with arbitrary thickness[J]. Laser Technology, 2014, 38(3):394-397(in Chinese). [18] ZHANG Y, HUANG Z H, ZHAO Z T, et al. In-place calibration of Stokes ellipsometer's instrument matrix[J]. Acta Optica Sinica, 2013, 33(2):0212002(in Chinese). doi: 10.3788/AOS [19] WANG Y H, ZHENG C L, ZHAO Z T. Muti-point calibration method based on Stokes ellipsometry system[J]. Chinses Journal of Lasers, 2012, 39(11):1108013(in Chinese). doi: 10.3788/CJL -
点击查看大图
图(4) / 表(1)
计量
- 文章访问数: 8055
- HTML全文浏览量: 6077
- PDF下载量: 286
- 被引次数: 0
