Two-step phase unwrapping based on swin-UNet-denoise and least square method
-
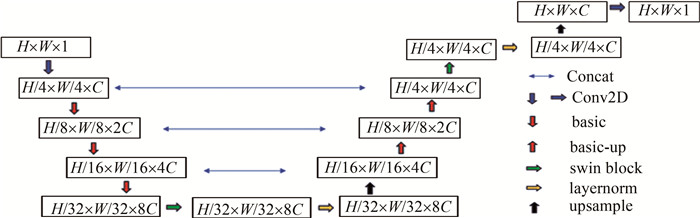
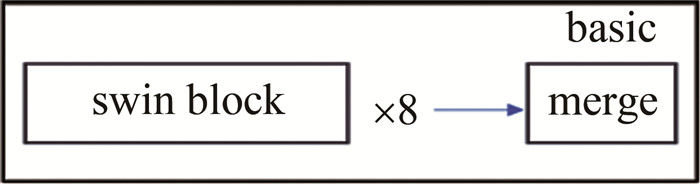
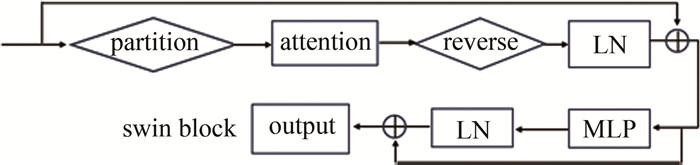
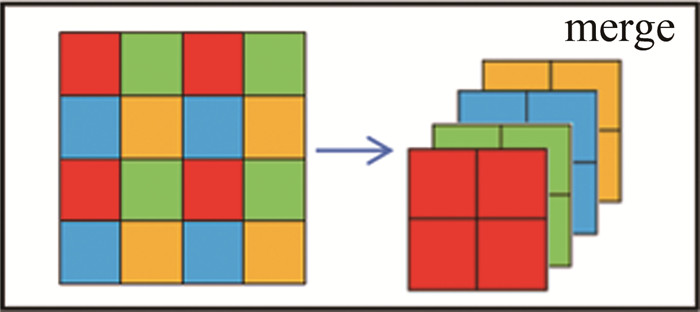
摘要: 相位解包裹在众多领域应用中都占有重要地位，但总会受到噪声的影响，尤其是散斑噪声。为了去除散斑噪声对包裹相位图的影响，并从中恢复出实际的相位值，采用两步法进行了理论分析和实验论证，从不同程度散斑噪声包裹的相位中恢复出绝对相位。以swin-UNet-denoise网络为基础，将swin block中的归一化层后置，并用余弦相似度计算注意力值，然后将相对位移偏移替换为对数位置偏移，并在上采样模块融合反卷积层以此提升网络的去噪能力；将去噪结果通过最小二乘法解包裹，再通过中值滤波获得绝对相位。结果表明，结构相似度为99.77%，峰值信噪比为39.98，均方根误差为0.4864，平均绝对误差为0.4302。所有网络只在300组仿真数据集上进行训练验证，证明即使在小样本的条件下，该研究也能为更快速、更高效、更准确地实现带有散斑噪声的相位解包裹提供参考。Abstract: Phase unwrapping plays an important role in many applications, but it is always affected by noise, especially speckle noise. In order to remove the effect of speckle noise on the wrapping phase diagram, the actual phase value was recovered from it. The two-step method was used to make theoretical analysis and experimental demonstration, and the absolute phase was recovered from the phase covered by speckle noise in different degrees. In the first step, based on the swin-UNet-denoise network, the normalized layer in swin block was set back, and the attention value was calculated by cosine similarity. Then, the relative displacement offset was replaced by logarithmic position offset, and the deconvolution layer was fused in the upsampling module to improve the denoising ability of the network. In the second step, the denoising result was unwrapped by least square method, and then the absolute phase was obtained by median filtering. The results show that the structural similarity is 99.77%, the peak signal-to-noise ratio is 39.98, the root-mean-square error is 0.4864, and the average absolute error is 0.4302, respectively. In addition, all the networks are only trained and verified on 300 simulation data sets, which proves that the research can provide a reference for faster, more efficient and accurate phase unwrapping with speckle noise even under the condition of small samples.
-
Keywords:
- holography /
- phase unwrapping /
- deep learning /
- least square method
-
-
![]()
图 8 训练过程中3种网络对验证集的峰值信噪比的变化
Figure 8. Change of the peak signal-to-noise ratio of three kinds of networks to the verification set during training
![]()
图 9 训练过程中3种网络对验证集的结构相似度的变化
Figure 9. Change of structural similarity of three kinds of networks to verification set during training
![]()
图 10 3种网络对于3种不同散斑程度相位图的去噪结果
Figure 10. Denoising results of three kinds of networks for three different speckle degree phase graphs
![]()
图 11 3种网络在不同散斑噪声下的均方根误差
Figure 11. Root mean square error of three kinds of networks under different speckle noise
![]()
图 12 3种网络在不同散斑噪声下的平均绝对误差
Figure 12. Average absolute error of three kinds of networks under different speckle noise
![]()
图 13 不同方法对不同噪声程度的解包裹结果
Figure 13. Unwrapping results of different methods with different noise levels
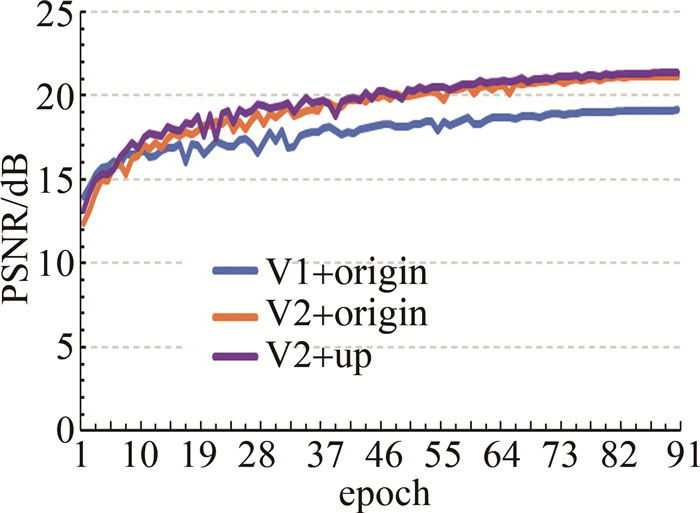
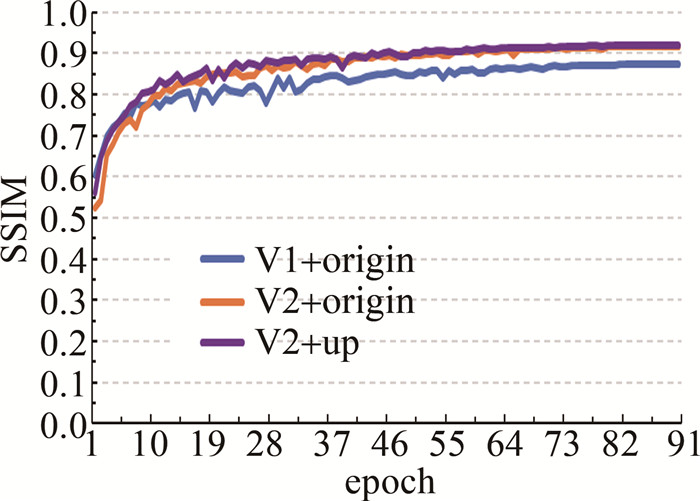
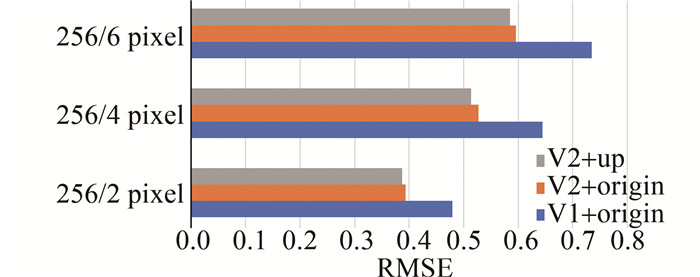
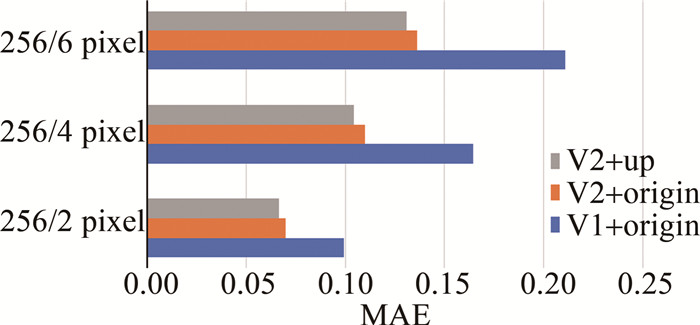
表 1 3种网络对测试集的评价指标的平均值
Table 1 Average value of the evaluation indexes of the three networks on the test set
mean SSIM PSNR RMSE MAE V1+origin 0.8803 20.4403 0.6196 0.1582 V2+origin 0.9211 22.2151 0.5053 0.1054 V2+up 0.9241 22.3827 0.4951 0.1005 
下载: 导出CSV
表 2 不同方法得到的解包裹结果的评价指标
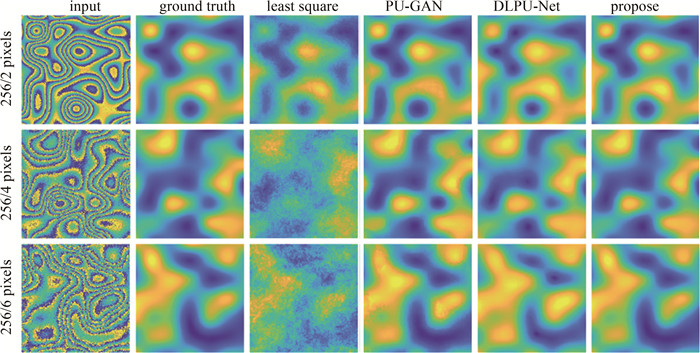
Table 2 Evaluation indexes of unwrapping results obtained by different methods
SSIM PSNR RMSE MAE least square 0.5344 9.6771 13.5715 12.0839 PU-GAN 0.9309 23.7721 3.0579 2.1431 DLPU-Net 0.9504 23.6297 3.0464 2.5411 propose 0.9977 39.9847 0.4864 0.4302
下载: 导出CSV
-
[1] GHIGLIA D C, PRITT M D. Two-dimensional phase unwrapping: Theory, algorithms, and software[M]. New York: Wiley, 1998: 1-59.
[2] YU H, LAN Y, YUAN Z, et al. Phase unwrapping in InSAR: A review[J]. IEEE Geoscience and Remote Sensing Magazine, 2019, 7(1): 40-58. DOI: 10.1109/MGRS.2018.2873644
[3] SONG S M, NAPEL S, PELC N J, et al. Phase unwrapping of MR phase images using Poisson equation[J]. IEEE Transactions on Image Processing: A publication of the IEEE Signal Processing Society, 1995, 4(5): 667-676. DOI: 10.1109/83.382500
[4] WYANT J C. Interferogram analysis: Digital fringe pattern measurement techniques[J]. Optical Engineering, 1993, 32(11): 2987-2988. DOI: 10.1117/1.OE.32.11.bookreviews
[5] GOLDSTEIN R M, ZEBKER H A, WERNER C L. Satellite radar interferometry: Two-dimensional phase unwrapping[J]. Radio Science, 1988, 23(4): 713-720. DOI: 10.1029/RS023i004p00713
[6] XU W, CUMMING I. A region-growing algorithm for InSAR phase unwrapping[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(1): 124-134. DOI: 10.1109/36.739143
[7] FLYNN T J. Consistent 2-D phase unwrapping guided by a quality map[C] //1996 International Geoscience and Remote Sensing Symposium. Lincoln, USA: IEEE Press, 1996: 2057-2059.
[8] FLYNN T J. Two-dimensional phase unwrapping with minimum weighted discontinuity[J]. Journal of the Optical Society of America, 1997, A14(10): 2692-2701.
[9] BONE D J. Fourier fringe analysis: The two-dimensional phase unwrapping problem[J]. Applied Optics, 1991, 30(25): 3627-3632. DOI: 10.1364/AO.30.003627
[10] GHIGLIA D C, ROMERO L A. Minimum LP-norm two-dimensional phase unwrapping[J]. Journal of the Optical Society of America, 1996, A13(10): 1999-2013.
[11] HYUN J S, ZHANG S. Enhanced two-frequency phase-shifting method[J]. Applied Optics, 2016, 55(16): 4395-4401. DOI: 10.1364/AO.55.004395
[12] ZHANG S. Digital multiple wavelength phase shifting algorithm[J]. Proceedings of the SPIE, 2009, 7432: 74320N. DOI: 10.1117/12.823903
[13] WANG K Q, LI Y, QIAN K M, et al. One-step robust deep learning phase unwrapping[J]. Optics Express, 2019, 27(10): 15100-15115. DOI: 10.1364/OE.27.015100
[14] ZHOU L, YU H, PASCAZIO V, et al. PU-GAN: A one-step 2-D InSAR phase unwrapping based on conditional generative adversarial network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-10.
[15] FANG Q, XIA H T, SONG Q H, et al. Speckle denoising based on a deep learning via conditional generative adversarial network in digital holographic interferometry[J]. Optics Express, 2022, 30(12): 20666-20683. DOI: 10.1364/OE.459213
[16] SPOORTHI G E, GORTHI S, GORTHI R K S S. PhaseNet: A deep convolutional neural network for two-dimensional phase unwrapping[J]. IEEE Signal Processing Letters, 2018, 26(1): 54-58.
[17] SPOORTHI G E, GORTHI R K S S, GORTHI S. PhaseNet 2.0: Phase unwrapping of noisy data based on deep learning approach[J]. IEEE Transactions on Image Processing, 2020, 29: 4862-4872. DOI: 10.1109/TIP.2020.2977213
[18] 陈翠茹, 王华英, 赵宝群, 等. 基于UMnet的数字全息相位解包裹[J]. 激光技术, 2023, 47(1): 73-79. DOI: 10.7510/jgjs.issn.1001-3806.2023.01.011 CHEN C R, WANG H Y, ZHAO B Q, et al. Digital holographic phase unwrapping based on UMnet[J]. Laser Technology, 2023, 47(1): 73-79(in Chinese). DOI: 10.7510/jgjs.issn.1001-3806.2023.01.011
[19] WANG K Q, KEMAO Q, DI J L, et al. Deep learning spatial phase unwrapping: A comparative review[J]. Advanced Photonics Nexus, 2022, 1(1): 014001.
[20] SILVIO M, PASCAL P. Quantitative appraisal for noise reduction in digital holographic phase imaging[J]. Optics Express, 2016, 24(13): 14322-14343. DOI: 10.1364/OE.24.014322
[21] FAN Ch M, LIU T J, LIU K H. SUNet: Swin transformer UNet for image denoising[C] //2022 IEEE International Symposium on Circuits and Systems (ISCAS). Austin, USA: IEEE, 2022: 2333-2337.
[22] LIU Z, HU H, LIN Y, et al. Swin transformer V2: Scaling up capacity and resolution[C]//2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orlean(LA), USA, IEEE Press, 2022: 11999-12009.
[23] HE K M, ZHANG X Y, REN S Q, et al. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification[C] //2015 IEEE International Conference on Computer Vision(ICCV). New Yorks, USA: IEEE Press, 2015: 1026-1034.
[24] QIAO X F. Information optics digital laboratory: Matlab edition[M]. Beijing: Science Press, 2015: 177-178(in Chinese).
计量
- 文章访问数: 877
- HTML全文浏览量: 5
- PDF下载量: 23