Improved iterative smoothing for correcting baseline in atomic emission spectra fitting algorithm
-
摘要: 为了解决光谱信号后续处理中基线影响的问题,提出了一种光谱信号区域基线拟合算法。从原始光谱中提取一定数量的较小数据点,并通过线性插值方法获得初始基线;在光谱存在重叠峰的情况下,选取的较小数据点可能包含非基线的异常点;引入了平滑迭代,提出用斜率变化率对基线进行判定的方法,将该算法与不同基线拟合方法在模拟光谱和实际光谱上进行了对比。结果表明,同其它方法相比,该算法在拟合模拟基线时,相对标准偏差最小,为8.25%;并且基于该算法获得的真实光谱定标曲线相关性最高,为99.85%;预测均方根误差最小,为0.5912。所提出的基线拟合算法在不同类型的原子发射光谱中均表现出高度准确性和稳定性,可以很好地估计原子发射光谱的连续背景。Abstract: To address the issue of baseline interference in the subsequent processing of spectral signals, a spectral signal region baseline fitting algorithm was proposed in this study. A certain number of smaller data points were extracted from the original spectrum, and an initial baseline was obtained through linear interpolation. In cases where there were overlapping peaks in the spectrum, the selected smaller data points may contain non-baseline outliers. Smoothing iterations were introduced, and a method for baseline determination based on the rate of change of the slope was proposed. This algorithm was compared with different baseline fitting methods on simulated and actual spectra. The results show that, in the process of fitting simulated baselines, a relative standard deviation of 8.25% is obtained with this algorithm, which is the lowest compared to that obtained with other methods. The correlation of the calibration curve based on this algorithm is the highest at 99.85%, and the smallest root mean square error in prediction is 0.5912. The baseline fitting algorithm proposed in this study demonstrates high accuracy and stability in various types of atomic emission spectra and can effectively estimate the continuous background of atomic emission spectra.
-
0. 引言
原子发射光谱是一种在元素分析领域广泛应用的光谱技术。它基于原子在受激条件下从激发态返回基态时发射特定频率的光谱现象,通过测量和分析这些发射谱线来确定样品中的元素种类及其相对含量。每种元素会在特定频率上拥有发射谱线。原子发射光谱技术同时具备多项优势,如分析速度快、检测限低、高灵敏度以及低成本,因此在冶金[1]、矿物学[2]、地质学[3]等众多领域广泛应用。然而,用光谱仪器获得的光谱信号存在各种干扰因素,其中包括样品中基体元素对有效光谱信号的干扰以及杂散光和暗电流干扰[4]。光谱基线的增大不仅会降低信背比,还可能影响元素后续定量分析的准确性,这会严重削弱原子发射光谱的分析能力。因此,进行基线校正是提取真实的原子发射光谱信号和实现背景消除的关键步骤。
常用的基线校正方法有迭代多项式拟合[5-6]、小波变换[7-9]、惩罚最小二乘[10-12]、非对称最小二乘[13-15]、连续背景极小点筛选分段拟合[16]等方法。非对称最小二乘算法方法虽然简单,但容易出现欠拟合现象。多项式拟合法[4]是通过最小二乘法确定多项式系数,来拟合光谱背景基线,但存在拟合基线高估的情况。小波变换[8]是进行光谱信号拆解,有助于分离低频和高频信号成分,但计算量和难度较大。加权惩罚最小二乘[10]是通过给谱峰设置小的权重,将峰值区域降低到基线,但谱峰会为基线估计带来干扰。由于原子发射光谱的数据量庞大且复杂,应用其它光谱背景校正方法时,会存在基线抬升、过拟合、欠拟合、稳定性差、不平滑等现象。
针对上述方法存在的问题,本文中提出了一种平滑迭代模型的原子发射光谱基线校正方法,通过窗口划分原始光谱区间,选取每个区间中一定数量的较小点,将较小点进行线性插值补全点数,通过平滑迭代滤波对插值后的数据处理,对比迭代前后各点斜率变化率,最终拟合出相应的光谱基线。该方法不仅能削弱因窗口宽度问题选取较小点出现异常点的问题,也能够利用平滑滤波实现异常点的优化,能获得很好的基线校正效果。
1. 基本原理
1.1 Savitzky-Golay平滑原理
基于最小二乘原理的Stavitzky-Golay(SG)滤波[17]是一种在移动窗口内进行加权多项式平滑。在原始光谱数据序列xi处左右各取M个数据,利用多项式拟合所获得的点预估出xi的数据。公式如下:
p(xi)=K∑k=0(akxki) (1) ε=argmin−M∑M[p(xi)−p0(xi)]2 (2) 式中:αk为滤波的多项式系数;ε为拟合曲线与原始光谱的残差;i为序列号;p0为原始光谱数据;k为多项式的阶次;p(xi)为平滑后的预估值。设置ε取最小值作为边界条件,求解可得多项式最佳系数。ε越小,则原数据拟合程度越好。平滑窗口在光谱中移动,每次移动步长为1。考虑到本文中是现实原子发射光谱的基线拟合,由于SG滤波的特点首尾端点处窗口长度不足,在用SG滤波的方法计算首尾两端处要具有光滑性,所以在首尾处要设定窗口一端长度不足时,将另一端的数据对称来补全窗口缺失部分的数据。
用SG滤波平滑迭代拟合光谱基线时,通过窗口取的较小点中会存在远高于基线的异常值点,异常点相对于基线是高频信号,则可视其为突变信号,当进行平滑时,异常点位置就会逐渐下降,但同时紧邻的光谱会逐渐升高。
1.2 改进的平滑迭代算法
SG滤波具有谱线平滑的特点,使用其拟合原子发射光谱基线的同时,又能对基线实现一定的平滑作用。故此,本文作者提出了改进的平滑迭代并用斜率变化率判定的拟合基线校正算法。
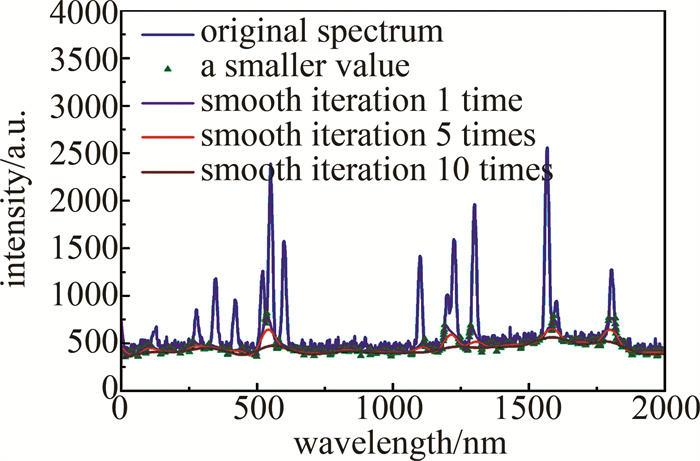
采用区间选取较小点,能够一定程度上预估出光谱基线的大致位置,但对于谱峰重叠较多的光谱来讲,区间选取较小点时,极有可能选取到重叠峰上的较小点,故对较小点要进行一定的处理,确保偏离基线的点能够被处理。通过SG滤波平滑迭代可以将偏离基线的异常点校正到基线位置,如图 1所示。图中点表示初始窗口选取的较小点,包括远离基线的异常点,通过对较小点形成的初始基线进行平滑,随着滤波次数增加异常点逐渐逼近基线。
由于异常点相对基线来讲是突变信号,在多次迭代后会逐渐逼近基线,可以通过对比迭代前后对应点斜率变化率来判断确定基线受异常点的影响情况,定义:
Kj(xi)=pj(xi)−pj(xi−1)xi−xi−1 (3) ΔK=Kj(xi)−Kj−1(xi)Kj−1(xi) (4) 式中:Kj(xi)为第j次滤波后点xi处的斜率;j代表迭代次数;ΔK为滤波前后斜率的变化率。
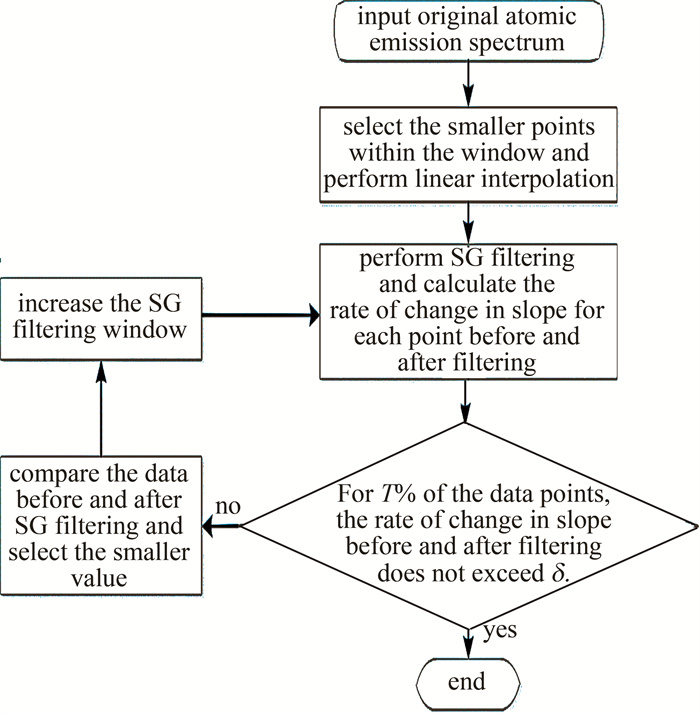
因此,本文中探讨了一种选取区间内较小值点的确定基线点、对异常点进行迭代平滑,并利用迭代前后各点处斜率变化率来判断拟合校正基线的方法,其流程图如图 2所示。通过采用SG滤波平滑算法,连续扩大SG滤波窗口,进行多轮迭代,逐渐趋向于光谱的基线。在原始光谱经过基线校正处理后,可获得校正后的光谱。光谱基线校正信号处理的步骤如下所述:(a)定义窗口。定义一个长度为N的窗口,窗口在原始光谱R中滑动,选取窗口中b个较小点,窗口滑动时不重叠,所有较小点进行线性插值,以生成平滑数据B;(b)进行SG滤波。对基线数据集合B进行SG滤波,用F表示滤波后的数据集合;(c)计算斜率变化率。使用1阶差分法计算数据集合F中各数据点的斜率变化率;(d)概率统计。对斜率变化率进行概率统计,以确定何时终止滤波。用差分法计算滤波前后各点的斜率和滤波前后各点的斜率变化率,设定一个阈值δ,如果超过T%的数据点的斜率变化率不超过阈值δ,则滤波结束国;(e)迭代。如果不满足概率统计条件,选择数据集合F和原始数据集合B中相应位置的较小值,生成新的数据集合R′,并增加SG滤波的窗口长度;(f)得到最优基线估计结果。重复步骤(b)~步骤(e),在斜率达到步骤(d)中的条件时,迭代结束。
在上述基线校正算法中引入N,b,δ,T4个调节参数。通过大量实验获取各类型合金样品的原子发射光谱,互补金属氧化物半导体(complementary metal oxide semiconductor, CMOS)的像素点个数为2048时,光谱谱峰信号点的个数在15~25个左右,窗口的取值N应大于谱峰信号点的个数,范围为30~40。b的取值不宜过大或过小,过大会在异常点会增多,增加后续平滑迭代次数,计算量增大;过小会在丢失部分有用的基线信息,后续拟合基线会存在偏差,故b的取值应为窗口长度的1/3~1/2之间。δ取决于迭代滤波逐渐增大的窗口宽度,窗口每次迭代增加的宽度越大,δ相对应也要增大,δ的取值范围为:0.0001~0.0004。D的取值需和δ配合。
这一方法的核心思想是通过SG平滑迭代滤波来逐步降低噪声和异常点的影响,以获得准确的光谱基线估计。同时,通过线性插值和斜率比较来处理光谱数据中的峰重叠和异常点,以确保最终光谱基线的估计结果准确可靠,这种方法适用于处理复杂的光谱数据。
2. 分析与讨论
2.1 基于模拟光谱验证算法性能
模拟光谱包含有15个高斯特征峰和信噪比为40 dB的噪声基线构成,包含2000个数据点。高斯特征峰计算公式[18]如:
f(λ)=Aexp[−(λ−μ)22σ2] (5) 式中:A为高斯函数峰值强度;μ为峰值位置的横坐标;λ为波长;σ是标准差表征控制峰的宽度。
综合考虑简便程度以及算法效果,较小点选取的窗口大小为32,每个窗口中选择较小的12个点,SG滤波初始窗口长度为20,每次迭代窗口加15,设定一个斜率变化率的阈值δ=0.2%,如果超过90%的数据点的斜率变化率不超过阈值0.2%,迭代终止输出最佳基线。
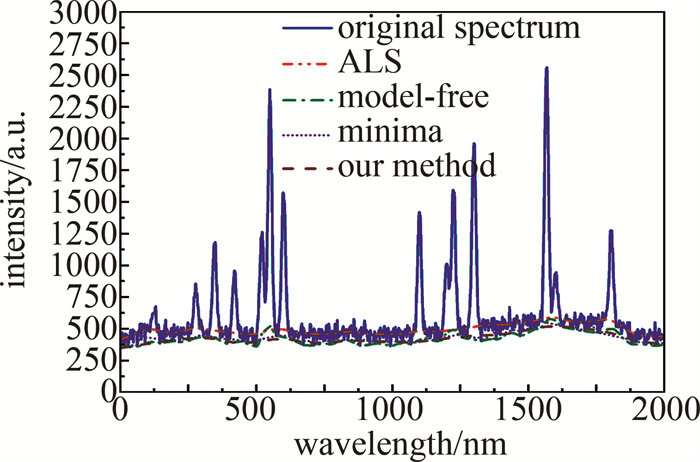
仿真光谱以及采用的非对称最小二乘[19](asymmetric least squares,ALS)、model-free方法[20]、minima方法[21]和本文中的方法得到的拟合基线如图 3所示。
由图 3可以看出,在拟合无峰处基线时,图中方法都对基线有较好的拟合效果,ALS方法出现了一定的基线高估情况;在拟合谱峰处基线时,model-free方法会在重叠峰处存在凸起,拟合准确度不高;在拟合小峰处基线时,minima方法偶尔会取到小峰处的点,导致基线稳定性降低。在3种不同类型的光谱中,本文中算法均获得了拟合准确的基线,具有较好的准确性、稳定性及平滑性。
为了更具体地比较不同方法对模拟光谱信号拟合的效果,采用不同方法预估出的基线,然后求取基线相对标准偏差(relative standard deviation, RSD)[22]。为了更详细地评估不同方法在拟合模拟光谱方面的性能,首先使用各方法拟合出的模拟光谱的基线,然后计算基线的相对标准偏差。较小的相对标准偏差表明经校正后的基线更加平稳,拟合效果更为优越,各方法拟合基线信号的相对标准偏差如表 1所示。由表中可以看出,与其它3种方法相比,本文中算法在模拟光谱数据中得到的RSD最小为8.25%,相对于minima拟合降低了25.14%,其在拟合基线时波动最小,拟合效果最好。
表 1 各方法拟合模拟光谱基线信号的RSDTable 1. RSD for spectral baseline signal fitting with various methodsmethod RSD/% ALS 9.61 model-free 11.68 minima 33.39 our method 8.25 根据表 1所示数据,本研究方法相对于其它3种基线拟合方法,在模拟光谱中获得了最小RSD。该结果表明,本文中所提出的算法有效地实现了光谱基线的平滑,降低了波动,同时获得了最佳的拟合效果。因此,该方法可有效拟合原子发射光谱的基线状况,从而提高后续定量分析的准确性。
2.2 实验及光谱校正
实验中采用自搭的光电激发光谱平台(激发光源电压为24 V,光源放电频率为400 Hz)以及自搭的激光诱导击穿光谱(laser-induced breakdown spectroscopy, LIBS)平台(激光器为Nd ∶ YAG脉冲激光器,波长为1064 nm,能量为50 mJ,频率为1 Hz)选取圆柱型低碳钢、镁合金、锌合金的标准样品。预处理利用车床将样品表面氧化层去除,避免影响后续定量分析结果。完成样品测试,获得原始原子发射光谱数据R。
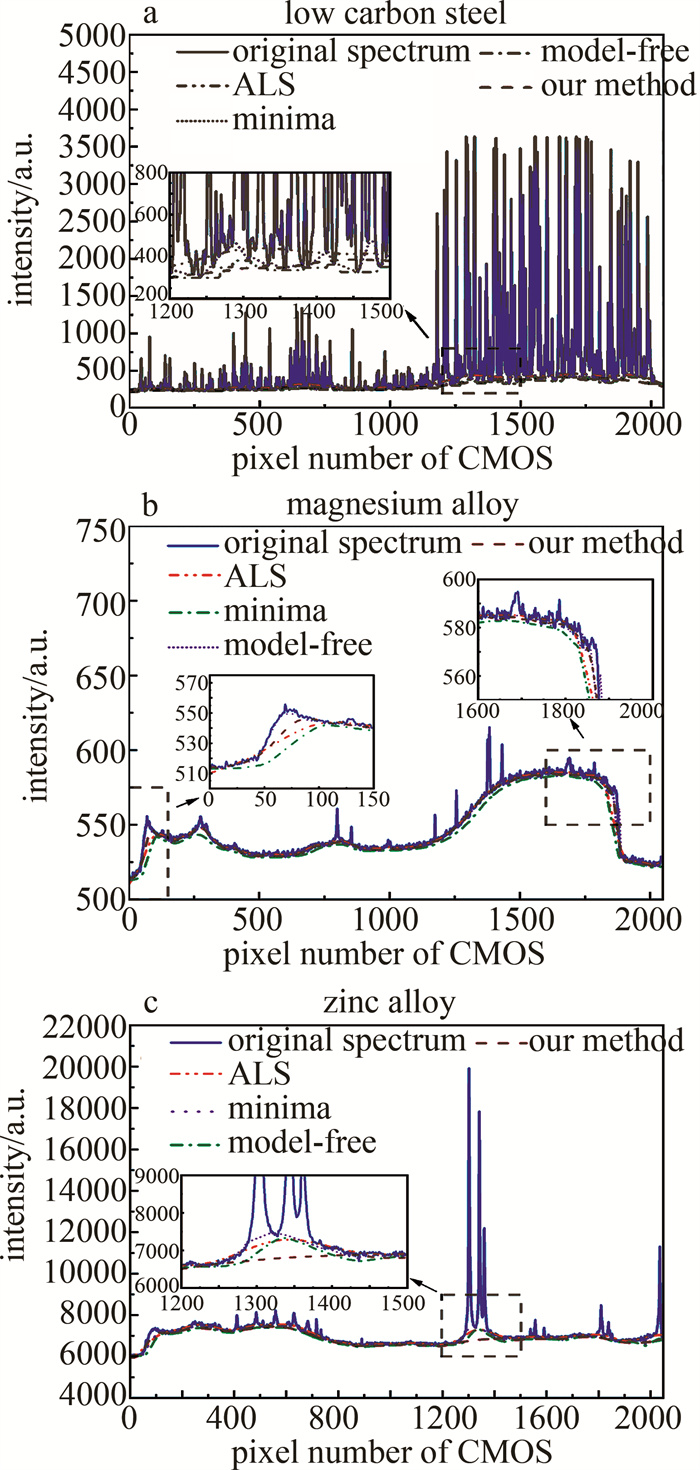
对3种方法与本文中的算法进行了比较。选择不同特征的原子发射光谱进行拟合基线对比验证算法,分别为光电激发的低碳钢标样光谱、光电激发的镁合金标样光谱、激光激发锌合金标样光谱,结果如图 4所示。
图 4a中minima方法对基线的拟合效果较好,但在谱峰附近拟合了周围的小峰;图 4b中信号区域基线曲率突变或者出现阶跃时,model-free方法基线拟合过低,拟合后的信号仍存在基线部分;图 4c中ALS方法得到的基线,在谱峰出存在凸起,基线拟合过高。当光谱区域基线曲率变化不大时,每种方法的的拟合结果很相近,当基线附近出现跃迁或小峰时,本文中算法较其它算法都更稳定、准确。综上所述,本文中算法在谱峰密度大的光谱中拟合基线,相比与其它方法不会存在基线高估的情况,同时也能保持较好的平滑性;在光谱信号区域曲率突变时,本文中算法较其它算法不会出现欠拟合的情况,能更准确、稳定得到拟合基线;在光谱较为稳定的区域,本文中算法表现出更小的波动性。
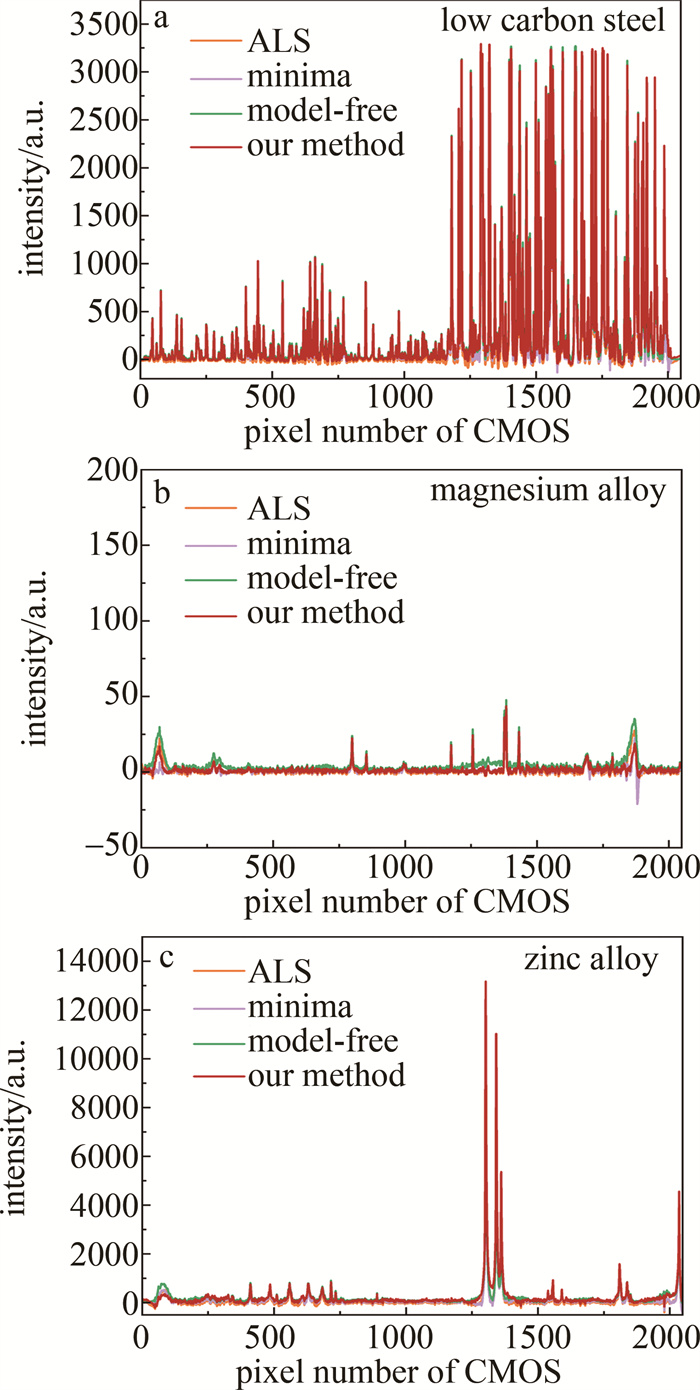
分别使用上述4种方法对3种原始光谱进行基线校正,校正后的光谱如图 5所示。通过比较本文中算法处理后的光谱底部较为平稳,保留各谱峰的强度较高;minima方法的整体光谱波动最大。
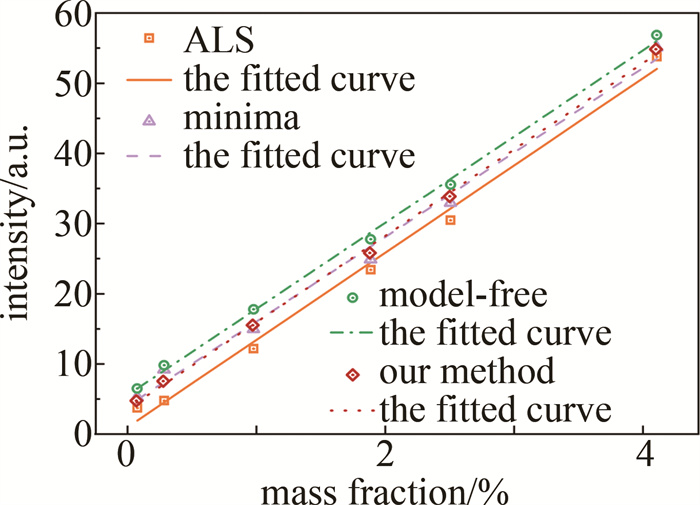
为了验证不同算法对元素定量分析的影响,将MgAlZn系镁合金标样中的锌元素作为定量分析对象,先用汞灯对光谱进行波长定标,再分别使用ALS、minima、model-free和本文中算法对镁合金标样光谱进行基线校正。图 6为对整体光谱数据进行基线校正后获取的有效光谱。选取255.794 nm特征谱线作为分析对象绘制的定量曲线,可以看出,4种去基线方法下的定量曲线模型都有良好的定量分析能力。
表 2为统计的各算法的锌元素定标曲线模型的相关系数R2和预测均方根误差(root mean square error prediction, RMSEP),可用来评价定量分析的准确度。相关系数越高证明定量分析模型越精准,本文中算法获得最大的相关性为99.85%,大于其它3种去基线方法,即本文中的算法基线校正方法处理后的样本数据的定标曲线更精准。预测均方根误差越小,说明定量分析的误差越小,由表 2可清晰看出,本文中算法的RMSEP仅为0.5912,相比minima方法预测均方根误差降低了80.96%。
表 2 定标曲线模型的相关系数和RMSEPTable 2. Correlation coefficients and RMSEP of calibration curve modelapproach R2/% RMSEP ALS 99.23 1.3563 minima 99.14 1.3924 model-free 99.78 0.7032 our method 99.85 0.5912 3. 结论
针对原子发射光谱存在的背景干扰强的问题,提出了一种改进的平滑迭代的光谱信号基线拟合方法。该方法通过窗口选取区间中较小点,进行插值计算出初始基线,通过SG迭代逐渐降低初始基线中异常值点对基线的影响,对比平滑迭代前后各点斜率变化率,判断基线中异常点的影响,直到迭代到异常点对基线的影响基本忽略不计,获得到最终的基线。本文中的算法不仅避免了拟合方法在谱峰区间出现的过拟合现象,相对于其它3种方法相比,还拥有较高的稳定性和平滑性。模拟光谱基线中得到基线的RSD最小为8.25%,相对标准偏差仅为minima拟合的24.7%,为model-free拟合的70.6%,为ALS拟合的85.8%。在实际光谱中,用4种方法拟合MgAlZn系镁合金标样光谱基线,将锌元素建立定量分析模型,本文中的算法获得最大的相关性为99.85%,大于其它3种去基线方法,且预测均方根误差最小为0.5912,比minima降低了80.96%。因此,本文中提出的算法能较好拟合原子发射光谱的基线,并能为光谱信号的定量分析提供更准确的信息,可以作为一种光谱基线拟合的有效手段。
-
表 1 各方法拟合模拟光谱基线信号的RSD
Table 1 RSD for spectral baseline signal fitting with various methods
method RSD/% ALS 9.61 model-free 11.68 minima 33.39 our method 8.25 表 2 定标曲线模型的相关系数和RMSEP
Table 2 Correlation coefficients and RMSEP of calibration curve model
approach R2/% RMSEP ALS 99.23 1.3563 minima 99.14 1.3924 model-free 99.78 0.7032 our method 99.85 0.5912 -
[1] 陆科呈, 卢祥丰, 顾沛沛, 等. 两种原子发射光谱法测定铝合金中高含量银的方法比较[J]. 理化检验, 2021, B57(5): 417- 419. LU K Ch, LU X F, GU P P, et al. Comparison on determination of high-content silver in aluminum alloy by two atomic emission spectrometric methods[J]. Physical Testing and Chemical Analysis, 2021, B57(5): 417- 419(in Chinese).
[2] 肖细炼, 朱园园, 陈燕波, 等. 交流电弧-光电直读发射光谱法测定岩石矿物样品中高含量锡[J]. 理化检验, 2021, B57(3): 241-246. XIAO X L, ZHU Y Y, CHEN Y B, et al. Determination of high content of tin in rock and mineral samples by alternating current arc-optoelectronic direct reading emission spectrometry[J]. Physical Testing and Chemical Analysis Part, 2021, B57(3): 241-246(in Chinese).
[3] 肖细炼, 王亚夫, 陈燕波, 等. 交流电弧光电直读发射光谱法测定地球化学样品中银硼锡[J]. 冶金分析, 2018, 38(7): 27-32. XIAO X L, WANG Y F, CHEN Y B, et al. Determination of silver, boron and tin in geochemical samples by alternating current arc opto-electronic direct reading emission spectrometry[J]. Metallurgical Ana-lysis, 2018, 38(7): 27-32(in Chinese).
[4] 夏果, 吴骕, 黄禅, 等. 交叉非对称型Czerny-Turner光谱仪光学系统设计[J]. 光子学报, 2017, 46(4): 0422003. XIA G, WU X, HUANG Ch, et al. Design of crossed-asymmetric Czerny-Turner spectrometer optical system[J]. Acta Photonica Sinica, 2017, 46(4): 0422003(in Chinese).
[5] HU H, BAI J, XIA G, et al. Improved baseline correction method based on polynomial fitting for raman spectroscopy[J]. Photonic Sensors, 2018, 8(4): 332-340. DOI: 10.1007/s13320-018-0512-y
[6] FENG X, ZHU Z, SHEN M, et al. The method of baseline drift co-rrection of Raman spectrum based on polynomial fitting[J]. Computers & Applied Chemistry, 2009, 26(6): 759-762. DOI: 10.3969/j.issn.1001-4160.2009.06.014
[7] 赵奉奎, 徐晓美, 吕立亚. 基于迭代小波变换的光谱信号本底扣除方法研究[J]. 分析测试学报, 2019, 38(10): 1275-1279. DOI: 10.3969/j.issn.1004-4957.2019.10.019 ZHAO F G, XU X M, LV L Y. A background removing method for spectrum signal based on iterative wavelet transform[J]. Journal of Instrumental Analysis, 2019, 38(10): 1275-1279(in Chinese). DOI: 10.3969/j.issn.1004-4957.2019.10.019
[8] LIU J, LIU S L, MEDHAT M E. Wavelet transform theory: The mathematical principles of wavelet transform in gamma spectroscopy[J]. Radiation Physics and Chemistry, 2023, 203: 110592. DOI: 10.1016/j.radphyschem.2022.110592
[9] BERTINETTO C G, VUORINEN T. Automatic baseline recognition for the correction of large sets of spectra using continuous wavelet transform and iterative fitting[J]. Applied Spectroscopy, 2014, 68(2): 155-164. DOI: 10.1366/13-07018
[10] ZHANG F, TANG X, TONG A, et al. An automatic baseline co-rrection method based on the penalized least squares method[J]. Sensors, 2020, 20(7): 2015-2026. DOI: 10.3390/s20072015
[11] YANG G, DAI J, LIU X, et al. Multiple constrained reweighted penalized least squares for spectral baseline correction[J]. Applied Spectroscopy, 2020, 74(12): 1443-1451. DOI: 10.1177/0003702819885002
[12] SHUANG B S, ZI Q Y, JIA X Z, et al. An improved dual asymmetric penalized least squares baseline correction method for high-noise spectral data analysis[J]. Nuclear Science and Engineering, 2023, 197(4): 589-600. DOI: 10.1080/00295639.2022.2132101
[13] 姜安, 彭江涛, 谢启伟, 等. 一种改进的非对称最小二乘基线校正算法[J]. 计算机与应用化学, 2012, 29(5): 537-540. DOI: 10.3969/j.issn.1001-4160.2012.05.006 JIANG A, PENG J T, XIE Q W, et al. An improved asymmetric least squares baseline correction algorithm[J]. Computers and Applied Chemistry, 2012, 29(5): 537-540(in Chinese). DOI: 10.3969/j.issn.1001-4160.2012.05.006
[14] ZHANG Q, LI H, XIAO H, et al. An improved PD-AsLS method for baseline estimation in EDXRF analysis[J]. Analytical Methods, 2021, 13(17): 2037-2043. DOI: 10.1039/D1AY00122A
[15] HE Sh X, ZHANG W, LIU L J, et al. Baseline correction for Raman spectra using an improved asymmetric least squares method[J]. Analytical Methods, 2014, 6(12): 4402- 4407. DOI: 10.1039/C4AY00068D
[16] SUN L, YU H. Automatic estimation of varying continuum background emission in laser-induced breakdown spectroscopy[J]. Spectrochimica Acta Part, 2009, B64(3): 278-287.
[17] 赵曼, 郭一新, 何玉青, 等. 改进的紫外拉曼光谱分段线性拟合基线校正方法[J]. 光谱学与光谱分析, 2020, 40(6): 1862-1868. ZHAO M, GUO Y X, HE Y Q, et al. Baseline correction of UV Raman spectrum based on improved piecewise linear fitting[J]. Spectroscopy and Spectral Analysis, 2020, 40(6): 1862-1868(in Chinese).
[18] 宁志强, 刘家祥, 吴越, 等. 基于改进迭代多项式拟合的红外光谱基线校正方法[J]. 激光与光电子学进展, 2020, 57(3): 033001. NING Zh Q, LIU J X, WU Y, et al. Infrared spectrum baseline correction method based on improved iterative polynomial fitting[J]. Laser & Optoelectronics Progress, 2020, 57(3): 033001 (in Chinese).
[19] EILERS P H C. Parametric time warping[J]. Analytical Chemistry, 2004, 76(2): 404- 411. DOI: 10.1021/ac034800e
[20] FRIEDRICHS M S. A model-free algorithm for the removal of baseline artifacts[J]. Journal of Biomolecular NMR, 1995, 5: 147-153.
[21] TAN B, HUANG M, ZHU Q, et al. Detection and correction of laser induced breakdown spectroscopy spectral background based on spline interpolation method[J]. Spectrochimica Acta Part, 2017, B138: 64-71.
[22] HU L, ZHAO N J, LIU W Q, et al. Study on removing method of continuous background spectrum in LIBS of multi-element heavy me-tals in water[J]. Chinese Journal of Lasers, 2014, 41(7): 0715003 (in Chinese). DOI: 10.3788/CJL201441.0715003



 下载:
下载: