1992年，DUNCAN等人提出了用光学扫描全息术(optical scanning holography, OSH)来记录全息信息，并随后得到了OSH的第1个实验结果^[1]。由于光学扫描全息术是通过2维的光学扫描快速获取样品的3维信息，并能够完整地重建物体图像，因此得到了越来越多研究人员的关注。近年来，这项技术在许多领域显示出广泛的应用潜力，比如扫描全息显微镜、3维图像识别、3维光学遥感、3维电视和显示器以及光学扫描加密等^[2-7]。在传统的光学扫描全息系统中，存在着重建图像由于丢失了高频信息成分而导致图像效果不佳的问题，许多学者因而提出了相应的提高成像分辨率方法，如双波长光源法、基于离轴全息图的超分辨率方法以及基于合成孔径的超分辨率成像等^[8-10]。由衍射理论可知，如果光瞳函数的空间分布发生改变，衍射斑点的强度分布也会随之改变，即所谓的切趾法^[11]。因此，通过设计合适的光瞳滤波器以提高分辨率效果，成为在超分辨率研究中的一种重要方法。

2010年，ZHOU等人首次提出了将随机相位编码技术应用于光学扫描全息术中的方案, 该方案需要在数据编码阶段将其中一个光瞳函数设计成随机分布的函数，而在重建解码阶段则使光瞳函数满足一定条件，从而将离焦层图像变成散斑噪声，然后通过设计合适的滤波器来滤除噪声，使聚焦层图像清晰地再现^[12]。2014年，WANG等人对基于随机相位编码的光学扫描全息(optical scanning holography based on random phase encoding, RPE-OSH)系统在衍射受限光瞳函数条件下的横向分辨率进行了分析，证明了双光瞳合成扫描系统的光学传递函数是光瞳函数的互相关，可以获得双极性的点扩散函数；并且通过MATLAB仿真比较了半月桥弯藻在RPE-OSH和OSH系统重建图像的效果，得到RPE-OSH系统重建图像和原图像之间的相关系数更高、重建图像频谱分布更接近于原图像、重建效果更好的结论^[13]。

本文中的主要目的是通过原理性的物理实验，验证WANG等人的理论模拟结果。通过比较同等实验条件下的RPE-OSH和OSH系统重建图像主观观看效果以及信噪比(signal-to-noise ratio, SNR)、相关系数(correlation coefficient, CC)和频谱曲线等客观指标，从实际物理实验的角度证实采用随机位相编码方法以改善光学扫描全息系统成像效果的可行性。

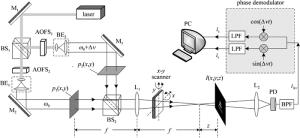
光学扫描全息是一种独特的实时全息技术，它通过一次2维光学扫描就可以获得3维物体的全息信息。OSH系统的原理图如图 1所示。由激光器发射频率为的光波，经过分光镜后分成两路光波。通过声光移频器(acousto-optic frequency shifter, AOFS)的调制作用，使两路光波产生Δν的频率差。然后这两束光波分别经过扩束镜BE₁和BE₂进行扩束，扩束后的光束分别被位于透镜L₁前焦面上的光瞳p₁(x, y)和p₂(x, y)所调制。随后，两路被调制的光波合束后再通过透镜L₁，把形成的汇聚波投射到x-y型两轴旋转台上的反射镜，通过运动控制器来控制光束，对位于透镜L₁后的物体进行逐点扫描。从物体透射出来的光被收集到光电探测器上，响应输出为携带有物体3维信息的电信号i(x, y)。i(x, y)由一个直流项和一个频率为Δν的交流电流项组成，经过中心频率设定在Δν的带通滤波器(band pass filter, BPF)后，得到外差交流信号i_Δν(x, y)，最后通过混频解调出物体的相位信息。图 1中，M为反射镜；BS(beam splitter)为分光镜；BE(beam expander)为扩束镜；t为时间；L为透镜；z为物体距离透镜L₁后焦面的距离；PD(photoelectric detector)为光电探测器；LPF(low pass filter)为低通滤波器；⊗为乘法器；p₁(x, y)和p₂(x, y)为光瞳函数；I(x, y; z)为物体透过率函数；i_c和i_s为外差电流的两路锁相输出电流。

Figure 1.  Schematic of OSH system

图 1所示的光学扫描全息系统中，若待测物体位于z=z_c处，则系统所记录的物体全息信号可表示为：

式中, 和^-1分别代表傅里叶变换和逆傅里叶变换，k_x和k_y代表空间频率，I(x, y; z_c)是物体的透过率函数，z_c表示编码阶段物体距离透镜L₁后焦面的距离, f_{OTF, Ω}表示该系统工作在差频为Ω下的光学传递函数，它与两个光瞳函数p₁(x, y)和p₂(x, y)有关：

式中, *表示复共轭，k₀表示波数，f是透镜L₁的焦距，P_1z和P_2z分别与p₁(x, y)和p₂(x, y)的傅里叶变换有关。

为了能够重建3维待测物体，还需要获得并记录位于不同位置z=z_d的点元物体(针孔)的全息信息, z_d为解码阶段针孔距离透镜L₁后焦面的距离。此时，相当于将(1)式中的待测物体更换为一个点元物体(针孔)，即I(x, y; z_d)=δ(x, y; z_d)。相应地，系统所记录的全息信号则表示为：

因此，对于光学扫描全息系统，其完整工作过程由(1)式和(3)式所代表的两个阶段组成，分别称为编码和解码阶段，最终重建结果是将上述两阶段所记录的全息信号进行卷积运算，从而得到^[14]：

对于3维的待测物体，处在z_d=z_c层的重建图像称为聚焦层，而处在z_d≠z_c的图像则称为离焦层。

无论是OSH还是RPE-OSH系统，其工作原理及过程都是如上所述，区别只是在光瞳函数的选取。在传统的OSH系统中，选取编码阶段的光瞳函数分别为:p_{1, c}(x, y)=δ(x, y)和p_{2, c}(x, y)=1，解码阶段函数则分别为p_{1, d}(x, y)=1和p_{2, d}(x, y)=δ(x, y)，此时(4)式可表示为^[15]：

从(5)式中可以看出，如果物体是由多层图像构成的，对于z_d=z_c的聚焦层，图像可以完全地重建出来，然而对于z_d≠z_c的离焦层，噪声则会表现为一个个模糊的图像出现在聚焦层图像上，这是不想看到的结果。

而在RPE-OSH系统中，编码阶段的光瞳函数为p_{1, c}(x, y)=exp [j2πs(x, y)]和p_{2, c}(x, y)=1，这里s(x, y)是以均匀概率分布在[0, 1]之间的独立随机变量；其解码阶段的光瞳函数为p_{1, d}(x, y)=1和p_{2, d}(x, y)，并且需满足条件：

式中, p_1，c^*(－x, －y)为p_{1, c}(－x, －y)的复共轭，此时可以得到^[12]：

通过利用相位恢复算法，可以反复地迭代运算p_{1, c}(x, y)和p_{2, d}(x, y)，使它们同时满足(6)式和下式^[12]:

这样，当z_d≠z_c时, 离焦层的图像则会以一个个随机信号出现在聚焦层上。随着距离|z_d-z_c|的增加，离焦层图像可以离散成均匀的背景噪声，距离越长，离焦层的图像更容易滤掉，从而对聚焦层图像的影响也越小。

由(6)式和(7)式来看，OSH系统与RPE-OSH系统重建的聚焦层图像似乎应当是一样的，但由于实际光学系统都受到光阑大小的限制，因此在聚焦层成像情况下，这两种系统的光学传递函数分别为^[13]:

式中, k₀D/f为与系统光阑尺度有关的参量(D为有效光瞳大小)，f_WOTF表示整个系统的光学传递函数，下标OSH和RPE-OSH分别对应OSH和RPE-OSH系统，rect代表矩形函数，T(k_x, k_y; z)由光瞳函数p_{1, c}^*(-fk_x/ k₀, -fk_y/k₀), p_{2, d}(fk_x/k₀, fk_y/k₀)和系统脉冲响应函数H(k_x, k_y; z)决定。因此，衍射受限的光学成像系统相当于一个低通滤波器。

光学传递函数是一个相对客观有效的评价光学系统图像质量的参量，它可以清楚地反映图像的不同频率成分的传递情况。光学传递函数的高频成分反映了保留细节信息的能力，而低频部分则反映了图像的轮廓信息^[16]。通过对比(9)式和(10)式可以发现，RPE-OSH系统的光学传递函数的截止频率更高。

图 2为所搭建的光学扫描全息系统原理性实验平台。实验中所用的主要参量如下:激光光源的波长λ=532nm；声光移频器采用PbMoO₄晶体，中心工作频率80MHz，在同步驱动电源的控制下，两个声光移频器使经分光镜出射的两路光波产生了1kHz的频率差，因此锁相放大器以及带通滤波器的工作频率也设定在1kHz；透镜L₁的焦距f=20cm，光学系统的有效光瞳大小D=5mm×5mm。与图 1不同的是，作者没有采用转镜偏折光束对物体扫描的方式，而是使用电动平移台在2维方向上移动物体。

Figure 2.  Test platform of OSH system

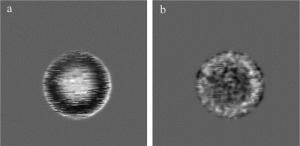
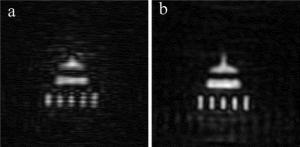
本文中的目的是比较OSH及RPE-OSH系统对聚焦层图像的重建效果，因此选用一张如图 3所示的泰姬陵图片作为被测物体，尺寸为1cm×1cm；点元物体则选用直径d=50μm的针孔；它们先后放置在距透镜L₁后焦面z=10cm处，扫描点数均为256pixel×256pixel。采用分辨率为1920×1080的空间光调制器来实现RPE-OSH方法中的随机位相编码光瞳分布函数；光电探测器则使用的是高灵敏度的硅光电池。按照前面所描述的方法，作者分别用OSH及RPE-OSH方法记录了被测物体以及针孔的全息图。图 4和图 5分别展示了所记录全息图的实部。

Figure 3.  Original image of object

Figure 4.  Real part of object hologram

Figure 5.  Real part of pinhole hologram

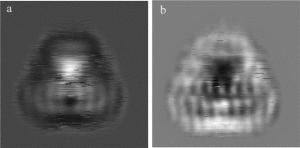
然后按照(4)式所述方法，对所记录的物体及针孔全息图进行图像重建运算, 得到两种方法下重建的物体图像，示于图 6a和图 6b中。显然，由于物体和针孔是在相同的位置上，所得到的是聚焦层重建图像。

Figure 6.  Reconstructed image of object

从图 6可以明显看出，在实验条件完全相同的情况下，RPE-OSH系统所重建的图像(见图 6b)比OSH的(见图 6a)主观感受要好。虽然由于实验设备等因素的局限，两幅重建图像的质量都不完美，但相比较而言，RPE-OSH系统重建的图像更为清晰一些。可以看到, 图 6b中的图像边缘信息保留得更加完整，图 6a中的图像则由于丢失了高频信息而更为模糊，且其背景噪声主要集中在图像附近, 也就是说，RPE-OSH系统保留了高频细节信息，重建图像具有更高的分辨率。

为了更客观地比较两种方法下重建图像的质量，计算了两幅图像相对于原始图像的信噪比和相关系数。信噪比的计算公式为：

式中, E_s和E_n分别为重建图像的信号能量及噪声能量; f (i, j)和n (i, j)均为M×N的矩阵; c′为最佳匹配系数，在实际计算中，c′可以通过计算原图像与重建图像的最小误差的平方和来求得。

相关系数的计算公式为：

式中, cov为协方差函数，F和G表示的是原图像和重建图像的频谱，D(F)和D(G)分别为F和G的方差，F和G表示的是F和G的均值，ρ_{F, G}的取值范围为[-1, 1]。

表 1是图 6中两种方法所重建的聚焦层图像和原图像之间信噪比和相关系数计算的结果。由表 1可知，RPE-OSH系统重建的图像具有更高的信噪比，而且重建图像和原图像之间有着更高的相关系数，这表明基于RPE-OSH系统重建的图像更加接近实际物体图像，保留了更多的细节信息。

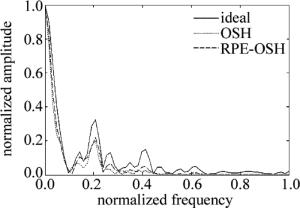
图 7为泰姬陵原图像、OSH及RPE-OSH重建图像的频谱情况。图像的频谱表征了图像含有的高低频率成分，因此重建图像的效果也可以用重建后的频谱与原图像频谱的接近程度来表示。显然，频谱与原图像越接近，说明重建的结果越接近真实还原。为了方便对比，将频谱的振幅和频率范围都做了归一化处理。从图中可以看出，在较低频区域，OSH和RPE-OSH重建图像的频谱几乎完全重合，说明它们对图像轮廓的还原能力相当；而在较高频区域，OSH重建图像的频谱与原图像频谱差异性明显，但RPE-OSH的频谱则与原图像频谱保持较好的变化趋势的一致性，这说明RPE-OSH重建的图像在图像细节还原上的失真没有OSH的那么严重。

Figure 7.  Relationship between amplitude and frequency of the original image and the reconstructed image

主要通过实验对比了RPE-OSH和OSH系统聚焦层图像的重建效果，从主观评价及信噪比、相关系数等客观参量的分析可以知道，正如理论模拟分析的那样，采用基于随机相位编码的光瞳函数能够改善OSH系统聚焦层图像的重建效果。在实验条件完全相同的情况下，RPE-OSH系统较传统OSH系统重建的图像更为清晰，具有更高的信噪比，同时与原图像之间相关系数更大，因而更接近真实物体。