Research process of data processing technology of full-waveform airborne laser radars
-
摘要: 全波形机载激光雷达可以直接快速获取地面特征点的3维空间位置,相比于其它测绘方法,全波形机载激光雷达在一定程度上性能更优。首先介绍了全波形机载激光雷达激光测距的工作原理,随后讨论了全波形机载激光雷达数据处理的一般性方法,并总结了其数据处理技术国内外研究现状的主要进展,最后归纳了全波形激光雷达数据处理研究中的关键问题,在此基础上对其数据处理的研究前景进行了展望。Abstract: 3-D space position of ground feature points can be quickly obtained by full-waveform airborne laser radars. Compared to other surveying and mapping methods, a full-waveform airborne laser radar has better performance to a certain extent. Firstly, the laser ranging principle of a full-waveform airborne laser radar is introduced. Then the general method of data processing for full-waveform airborne lidar is discussed. The main progress and the research status of data processing technology at home and abroad are summarized. Finally, the key problems in the research of full-waveform lidar data processing are summarized. On this basis, the research prospect of data processing is prospected.
-
Keywords:
- laser technique /
- laser range finder /
- data processing /
- deconvolution /
- waveform decomposition
-
引言
作为一种新兴的空间对地遥感观测手段,激光雷达(light detection and ranging, LiDAR)是在传统雷达和光电辐射探测的基础上发展起来一种主动探测技术。它将激光技术与测绘技术集于一身,集成了全球定位系统、高精度扫描仪、3维激光测距仪和惯性导航系统,通过发射激光束测量雷达系统与地物目标之间的距离和位置等特征信息,进而获取高精度的地物3维空间信息。相对于微波雷达而言,激光雷达在测量精度、分辨率和抗干扰能力等方面具有一定的优势,所以成为获取地球空间信息的重要技术手段之一。目前,激光雷达测量技术的发展已日趋成熟,并已在城市3维建模、数字水利工程和灾害监测等应用领域得到了广泛的推广[1]。然而,由于激光雷达获取的回波数据为不规则的离散点数据,在后续数据处理时,需要采用准确有效的数据处理方法才可反演得到原始的特征信息。
1. 全波形机载激光雷达
2004年,奥地利RIEGL公司研制生产了第1套商用型小光斑全波形机载激光雷达测量系统LMS-Q560。系统发射的激光脉冲在与地物目标作用之后,所形成的后向散射脉冲回波信号由测量系统以较高的采样率进行采样,并对脉冲信号强度进行数字量化和记录。全波形机载激光雷达系统的后向散射脉冲回波信号是发射激光脉冲与其光斑照射范围内所有地物目标相互作用后的回波信号能量及背景噪声的叠加。与传统的激光雷达相比,用户可以根据需要对回波波形进行分解以得到多个感兴趣的信息。系统一经问世,立刻引起了众多学者的关注,开启了对全波形激光雷达数据处理研究与应用的新时代[2]。
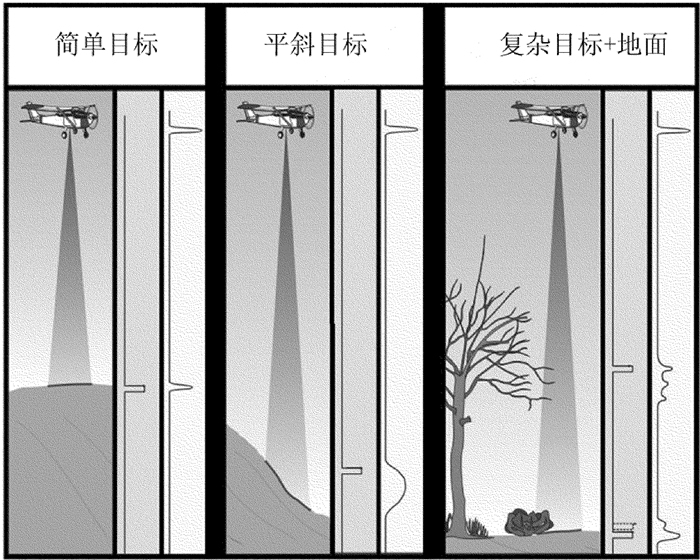
图 1中展示了传统/全波形机载激光雷达在扫描不同对象时得到的离散回波信号及全波形结果。对于离散回波信号,传统激光雷达仅仅记录了有限次的离散回波信号(通常是第1次和最后一次)[3];而对于全波形机载激光雷达,系统发射端发出的激光束在与其光斑照射范围内的多个地物目标相互作用之后,系统接收端则以较高的采样频率对回波进行采样并数字化,从而得到与地物目标作用的先后顺序相同的回波信号。不同的地物目标得到的回波信号差距很大,当系统发射的激光脉冲遇到较高的地物面时回波信号变窄,遇到倾斜的地物面时回波信号波形展宽且波形强度也会有不同程度的变化。若不同高度的地物目标间距很近,则系统接收的回波信号往往是多个小波叠加的结果,加之各种噪声的影响,因此必须对回波数据进行有效分解和处理,以将每个地物目标的回波从接收到的波形数据中一一分离,用以准确获取每个地物目标的相关信息[4]。
2. 全波形机载激光雷达数据处理方法及其研究现状
目前,全波形机载激光雷达的数据处理方法主要有两种:反卷积法和波形分解法。这两种方法均可以得到较为理想的结果,但在原理和处理过程上有所不同。本文中将对这两种方法的实现原理和研究现状进行介绍和归纳,并对波形分解法做重点介绍。
2.1 反卷积法
假设全波形激光雷达的发射脉冲和地物目标的作用过程等效于一个卷积的过程,回波信号的波形则是发射波形与地物目标的卷积响应,在发射波形和回波波形已知的情况下,所需了解的地物目标的特征就是求解反卷积的过程,可表示为:
p(t)=s(t)∗h(t)+n(t) (1) 式中,p(t)表示回波信号,“*”表示卷积,s(t)表示发射激光脉冲,n(t)为回波信号中所含的噪声成分,h(t)为所求的地物目标的特征波形函数[5]。
2006年,JUTZI等人[6]首次提出对全波形数据使用反卷积法,先去除回波信号中的噪声,接着基于傅里叶变换的方法实现发射脉冲和回波信号的反卷积变换,然后采用维纳滤波还原地物目标表面的响应函数,最后使用列文伯格-马夸尔特(Levenburg-Marquardt,L-M)算法迭代优化了目标表面响应函数的参量;实验结果表明,该算法可以有效提取高差大于15cm的目标物。2011年,ANDREAS[7]针对波形处理时反卷积法的固有病态问题,采用B样条辅助的反卷积法对波形进行了重新拟合,并得到了不同待测目标的后向散射截面;但是经B样条处理后的运算复杂度却大大增加,波形的特征也容易丢失。2016年,为了更加有效地复原待测目标的横截面,AZADBAKHT[8]通过具有稀疏约束特性的正则化方法首次实现了反卷积运算,并通过L曲线法优化了正则化参量;实验表明,该方法中的反卷积信号没有出现其它卷积实现方法中的振荡和负幅值,因而在消除系统参量对波形的影响和重建目标横截面等方面性能更为优越。2017年,SHEN等人[9]基于B样条建模技术,提出了一种新型波形分解算法;针对不具有先验形状的雷达波形,以RIEGL公司的回波波形为例进行分解,采用B样条建模并将回波波形视为发射激光脉冲的有限次平移和缩放的混合;该方法较以高斯波形分解而言,拟合残差减少了6.4%,由于B样条的灵活性,该方法更适用于对各种全波形激光雷达数据进行建模。随后,ZHOU[10]全面比较了直接分解法、理查德森-路西(Richardson-Lucy,R-L)反卷积法和戈德反卷积法3种方法;实验结果表明,当空间差异在0.5m~1m范围时,直接分解法的性能优于其它两种, 在植被分布稀疏的区域,R-L反卷积法表现较好,而戈德反卷积法在植被分布密集的区域具有较好的表现,且能够获得的有效回波数量更多。
虽然反卷积法受雷达系统参量和自然环境特征的影响较小,但由于反卷积法实现复杂,所以反卷积法在数据分解处理方面的研究与应用还有待进一步完善。
2.2 波形分解法
波形分解法中,回波信号的波形看作为光斑照射范围内不同地物目标对发射激光脉冲散射后的综合作用结果。波形分解方法是将回波波形分解成为一系列的分量和噪声和的形式,其中,每个分量代表光斑内不同地物目标的相应的回波信号,通过提取每个分量即可达到提取相应地物目标结构特征信息的目的,因此回波信号波形可以表示为:
f(x)=b+n∑i=1fi(x) (2) 式中,f(x)表示雷达回波信号波形,b表示噪声,n为照射光斑内有效的反射面数量,fi(x)表示第i个地物目标的回波波形[5]。由于不同地物目标与发射激光脉冲作用之后的回波波形不同,且不同雷达系统发射的激光脉冲形状也不尽相同,因此,在对回波波形进行拟合的时候,就需要根据不同的情况,选择合适的核函数进行拟合[11]。
2006年,针对第1个全波形小光斑激光雷达RIGEL-LMS-Q560,WAGNER等人[12]通过雷达方程证明了以高斯函数为核函数并采用最大期望算法分解回波波形的有效性,成功获取了各组分的距离、振幅、回波宽度等分量信息,较好地实现了系统回波数据的拟合且拟合率高达98%,为波形数据的分解提供了科学的理论依据;但是对于某些非平面目标及回波波形非对称的情况,以高斯函数作为核函数则会产生较大的误差。2007年,CHAUVE等人[13]针对波形非对称的回波信号分别以高斯函数、广义高斯函数和对数正态分布函数作为核函数对波形进行分解;实验结果表明,对数正态分布函数的拟合效果最差,广义高斯函数取得的效果普遍好于高斯函数和对数正态分布函数。2017年,BRUGGISSER等人[14]针对森林地区的独特的回波数据,提出使用偏正态分布函数(skew normal distribution,SND)作为核函数实现波形分解;与传统的高斯核函数相比,使用SND可以同时对对称和非对称的回波进行建模,不仅可以获取距离、振幅和回波宽度信息,还可以获得回波的偏斜度和回波峰度信息,为后续植被物种分类应用中获得高分类正确率提供了有力保障。
波形分解法主要有3个步骤:(1)回波波形去噪;(2)参量初值估计;(3)优化参量拟合回波波形。
2.2.1 回波波形去噪
由于受到环境、雷达系统参量等因素的影响,回波波形不可避免地包含着大量的噪声,因此非常有必要对回波波形进行预处理,以去除系统中振铃效应所形成的噪声和后向散射噪声。目前,全波形激光雷达回波波形去噪的方法主要有阈值法、低通滤波、经验模态分解、小波去噪等[15]。
2013年,AZADBAKHT等人[16]使用基于奇异值分解的塞瓦德金-戈利(Savitzky-Golay,S-G)低通滤波器对波形进行去噪,并基于多项式和局部最小二乘法拟合和平滑波形,取得了较好的去噪效果。2015年,HE[4]比较了阈值法、频域低通滤波和小波去噪3种方法的去噪效果;其中,阈值法实现过程简单,但是存在噪声估计过小和高频噪声难以去除的问题,频域低通滤波法则无法兼顾去噪效果和波形特征保留的问题,小波去噪法虽然可以有效保留波形特征并取得良好的去噪效果,但是不同的去噪参量(如分解和重构尺度、阈值参量和小波基函数等)对去噪效果影响较大,在选择合适的去噪参量时需要反复考量。2016年,DAI[17]提出采用经验模态分解和分数阶傅里叶变化相结合的方法实现回波信号去噪; 其中,经验模态分解可以从数据中自适应的得到基函数,克服小波去噪中去噪参量可能引入的不确定性,但是简单地舍弃高频分量又会造成信号的损失或者去噪效果不好;通过引入分数阶傅里叶变换,可以选取特定的分量进行进一步处理,进而在一定程度上降低了舍弃高频分量所带来的影响。2017年,LIANG等人[18]采用高斯滤波法对回波数据进行去噪处理,通过设置高斯函数的宽度和滤波模板长度研究获得了不同的去噪效果;实验结果表明,将发射脉冲半宽作为高斯函数宽度且滤波模板为时,滤波后的数据既能达到噪声抑制和平滑的目的,又能最大程度保留回波波形的原始特征。
2.2.2 参量初值估计
在波形分解中,初始参量估计是非常重要的环节,其目的是为了确定地物目标有效的回波数量并准确拟合每个地物目标函数所需要的初值。由于测量环境地形复杂,且回波信号及噪声在地物目标间可能存在多次漫反射,致使回波中包含了很多难以识别的弱波和叠加波,因此如何确定波形的分解数和初值存在一定的难度。目前已有的参量估计方法包括峰值法、重心法、赤池信息准则、拐点法等。
2005年,SODERMAN等人[19]借助赤池信息量准则对波形中的每个分组进行了估计,通过计算最大期望值成功实现了每个数据点的分类,但是当回波信号波形复杂且信号的去噪效果不佳时,算法的分解精度则较低。2009年,武汉大学的MA等人[20]采用改进的最大期望算法对波形分解中的参量进行了估计和优化;与传统的非线性优化算法相比,该算法不需要执行最小二乘拟合,但是若仅使用1阶导数进行波形检测,则难以识别出不明显的叠加波。2010年,LIN[21]提出了一种严格脉冲监测算法;该算法基于高斯分解,通过计算波形的2阶导数和明显峰值点两侧的样本数目发现重叠波,迭代拟合过程中在高残差的情况下寻找弱波,从而确定波形分量个数;该算法提高了叠加波与弱波的识别率,在双目标的回波样本测试中,表现要优于重心法和高斯脉冲拟合法,但是算法过程太过复杂,实用性有限。2013年,LAI等人[22]提出一种新型的波形分解方法,通过层层剥离的策略实现了波形分量特征参量初值的估计,即每次通过波形中的最大值作为波峰值,从而确定1个高斯分量和3个预估特征参量,并将其从波形数据中分离出来,然后在剩下的波形中继续寻找波峰值,确定下一个高斯分量和预估特征参量,直到剩下的波形中没有值大于所设定的阈值,此时剥离结束; 另外,还引入有限内存的布洛伊登-弗莱彻-戈德法布-香农(limited-memory Broyden-Fletcher-Goldfarb-Shanno,L-BFGS)算法对波形分量特征参量的预估值进行了优化,进而有效检测出了复杂的重叠波和弱波。2014年,DUAN[23]提出一种高斯拐点匹配法,将平面曲线离散点/拐点查找算法检测到的拐点与右边第1个点连成直线,若直线斜率大于零则为左拐点,反之为右拐点,通过左右拐点的匹配确定高斯分量的个数,进而减少伪拐点的影响。2015年,ZHAO[24]提出可变分量高斯混合模型及可逆蒙特卡洛-马尔科夫链(reversible jump Markov chain Monte Carlo,RJMCMC)算法,借助高斯混合模型对实际波形数据进行了拟合,依据能量函数定义得到了吉布斯分布并表征了数据的或然率、描述了其拟合程度,然后用贝叶斯定理刻画出波形分解的后验概率模型,通过RJMCMC算法模拟后验概率模型得到了波形分解个数及各高斯分量参量,有效实现了波形分解; 对于大部分波形而言,该方法拟合程度较高,但是对于一些非对称、倾斜或者具有拖尾特征的波形而言,拟合精度有限。
2.2.3 优化参量拟合回波波形
参量初值估计确定了待拟合函数的初值,而通过最小化回波波形和拟合波形之间的误差则可以达到参量优化的目的。两者之间的误差函数可以用多个指标表达,最常用的是借助均方根误差表达,如下式所示:
yRMSE=√1n∑[y−f(x)]2 (3) 式中,yRMSE是均方根误差(root mean square error, RMSE)的值,y是原始回波数据,f(x)是拟合之后的数据。经优化算法优化之后计算均方根误差,均方根误差越小,回波拟合的程度则越高。目前最常用的优化算法包括基于非线性最小二乘法的L-M算法、最大期望算法、拟牛顿法、可逆蒙特卡洛-马尔科夫链算法等。
2016年,WANG[25]提出了一种基于分组L-M算法的高斯分解方法,并对全波形机载激光雷达数据进行了分解处理,首先根据定义域将待优化的参量进行分组,然后对各组参量按照定义域的限制依次进行了优化; 分组L-M算法在一定程度上有效避免了算法中初值雅克比矩阵引入的非数值问题,但是在优化速度方面,该方法明显低于传统的L-M算法。随后,为了防止L-M算法依赖初值陷入局部最优解,DAI等人[26]将随机搜索的粒子群算法与L-M算法相结合,将粒子群算法得到的解作为L-M算法的初值,进而将雷达回波信号分解为一系列的单个波形的叠加; 经验证,该方法能够将波形的拟合精度提高至98.9%,有效地提高了回波分解的精度,但是,在面对多峰或者重叠波较多的情况,粒子群算法的收敛性则较弱。2017年,LIANG等人[27]提出了一种优化的L-M方法; 该方法在传统L-M方法上通过在迭代的过程中根据定义的误差内积值的变化判断是否更新雅可比矩阵以及调整阻尼系数,有效提高了计算速度,得到的残差值也有所降低。
针对全波形机载激光雷达中的回波信号处理技术,各国学者一直在开展着相关算法和应用研究,努力挖掘雷达系统所获得的深度及广度信息。由于可以提取获得回波波形中的额外信息,波形分解法已成为目前使用最多的方法。但是,受到复杂地形及地物目标特征多样等因素的影响,雷达系统的回波信号多种多样,无法用单一波形进行准确拟合,因此,在未来的信号处理技术研究中应当选择更为合适有效的拟合函数。而在回波波形去噪环节中,寻找一种既能较好地抑制噪声又能最大限度地保留波形特征的滤波方法也是十分必要的。另外,在波形分解中,回波分量的数目和初值至关重要,由于这一过程是不可逆的,一旦出现错误,将会给后续参量优化及波形拟合带来严重影响,因此,寻找一种更加有效的检测方法至关重要。目前,各国学者所提出的参量优化方法大多都是围绕如何避免L-M算法出现奇异雅可比矩阵、如何缩减算法的运算时间、如何跳出局部最优解和提高拟合精度等问题提出的,除此之外,还可以寻找一些收敛效果明显且运算速度更好的算法,或者采用随机搜索、智能仿生算法与传统算法相结合的思路,以进一步提高算法的全局收敛能力及运算速度。
3. 结论
全波形机载激光雷达技术的发展,为获取高时空分辨率的地球空间信息提供了全新的技术手段,数据的获取从人工测量变为自动获取,并朝着智能获取的方向发展,提高了地物目标的观测精度和速度,同时可以快速地获取地面特征点的3维空间位置和地表的形态特征,因而在遥感测绘等领域具有明确的应用前景,并已得到了广泛的关注和快速的发展。其中,回波信号的提取及处理技术尤为重要,特别是面对地物结构复杂等现实情况,并且信号滤波算法的判断条件也无法一一适应各种地物地貌特征且各种数据处理算法也有各自的不足之处。因此,有关全波形激光雷达的数据后处理技术研究仍有待进一步完善,其依旧是激光雷达测量技术研究领域的研究热点和难点。未来,在全波形机载激光雷达数据处理方面,仍有很大的发展潜力和空间,特别是在智能滤波和地物目标分类等方面。
-
[1] ZHANG X H. Theory and method of airborne lidar measurement technology[M]. Wuhan:Wuhan University Press, 2007:9-17(in Chinese).
[2] WANG J H, LI Ch R, ZHOU M. Airborne full-waveform lidar data processing and application[J]. Foreign Electronic Measurement Techonolgy, 2012, 31(6):71-75(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/chtb201301003
[3] WANG J H. Research on the key techniques of the airbornelidar data processing[D]. Wuhan: Huazhong University of Science and Technology, 2012: 5-8(in Chinese).
[4] HE L. Research on small-footprint als full-waveform data processing technology[D]. Chengdu: University of Electronic Science and Technology of China, 2015: 1-34(in Chinese).
[5] XU G C. Research on airborne lidar waveform data processing and classifying[D]. Nanjing: Nanjing Forestry University, 2010: 13-17(in Chinese).
[6] JUTZI B, STILLA U. Range determination with waveform recording laser systems using a wiener filter[J]. ISPRS Journal Photogrammetry and Remote Sensing, 2006, 61(2):95-107. DOI: 10.1016/j.isprsjprs.2006.09.001
[7] ANDREAS R, GUNTHER B, NORBERT P. B-spline deconvolution for differential target cross-section determination in full-waveform laser scanning data[J]. ISPRS Journal Photogrammetry and Remote Sen-sing, 2011, 66(4):418-428. DOI: 10.1016/j.isprsjprs.2011.02.002
[8] AZADBAKHT M, FRASER C, KHOSHELHAM K. A sparsity-based regularization approach for deconvolution of full-waveform airborne lidar data[J]. Remote Sensing, 2016, 8(8):648-674. DOI: 10.3390/rs8080648
[9] SHEN X, LI Q Q, WU G, ZHU J. Decomposition of lidar waveforms by b-spline-based modeling[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 128(6):182-191. http://www.sciencedirect.com/science/article/pii/S0924271616303306
[10] ZHOU T, POPESCU SC, KRAUSE K, et al. Gold-a novel deconvolution algorithm with optimization for waveform lidar processing[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 129(7):131-150. http://www.sciencedirect.com/science/article/pii/S0924271616304968
[11] JIAO Y T, XING Y Q, HUO D, et al. A review on full-waveform airborne lidar data processing and it application to forestry[J]. World Forestry Research, 2015, 28(3):42-46(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/sjlyyj201503008
[12] WAGNER W, ULLRICH A, MELZER T, et al. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(2):100-112. DOI: 10.1016/j.isprsjprs.2005.12.001
[13] CHAUVE A, MALLET C, BRETAR F, et al. Processing full waveform lidar data:modeling raw signals[J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2007, 36(52):102-107.
[14] BRUGGISSER M, RONCAT A, SCHAEPMAN M E, et al. Retrie-val of higher order statistical moments from full-waveform lidar data for tree species classification.Remote Sensing of Environment, 2017, 129(7):28-41. http://www.sciencedirect.com/science/article/pii/S0034425717301840
[15] XU F. Research and implementation of en/decoding and signal processing technologies for array-modulated 3-D imaging lidar[D]. Nanjing: Nanjing University, 2016: 71-87(in Chinese).
[16] AZADBAKHT M, FRASER C S, ZHANG C, et al. A signal denoising method for full-waveform lidar data[C]//ISPRS Workshop Laser Scanning 2013. Germany: Copernicus GmbH, 2013: 31-36.
[17] DAI C. Lidar echo signal enhancement and waveform decomposition[D]. Nanjing: Nanjing University, 2016: 21-31(in Chinese).
[18] LIANG M, MA K. Study on the method of echo signal denoising based on gauss filter[J]. Geomatics and Spatial Information Technology, 2017, 40(1):40-42(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dbch201701011
[19] SODERMAN U, PERSSON A, TOPEL J, et al. On analysis and visualization of full-waveform airborne laser scanner data[C]//Conference on Laser Radar Technology and Applications Ⅹ. Orlando, USA: International Society for Optics and Photonics, 2005: 184-192.
[20] MA H Ch, LI Q. Modified em algorithm and its application to the decomposition of laser scanning waveform data[J]. Journal of Remote Sensing, 2009, 13(1):35-41. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ygxb200901004
[21] LIN Y C, MILLS J P, SMITHVOYSEY S, et al. Rigorouspulse detection from full-waveform airborne laser scanning data[J]. International Journal of Remote Sensing, 2010, 31(5):1303-1324. DOI: 10.1080/01431160903380599
[22] LAI X D, QIN N N, HAN X Sh, et al. Iterative decomposition method for foot-print lidar waveform[J]. Journal of Infrared and Mi-llimeter Waves, 2013, 32(4):319-324(in Chinese). DOI: 10.3724/SP.J.1010.2013.00319
[23] DUAN Y H, ZHANG A W, LIU Zh, et al. A gaussian inflexion points matching method for gaussian decomposition of airborne lidar waveform data[J]. Laser and Optoelectronics Progress, 2014, 51(10):102801(in Chinese). DOI: 10.3788/LOP
[24] ZHAO Q H, LI H Y, LI Y. Gaussian mixture model with variable components for full waveform lidar data decomposition and RJMCMC algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12):1367-1377(in Chinese).
[25] WANG S Y, MA H Ch, WANG J D, et al. Gaussian decomposition of full-waveform lidar based on grouping LM algorithm[J]. Geoma-tics and Spatial Information Technology, 2016, 39(7):144-147(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-DBCH201607046.htm
[26] DAI C, WANG Y Q, XU F. 3-D lidar echo decomposition based on partical swarm optimization[J]. Laser Technology, 2016, 40(2):284-287(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-JGJS201602028.htm
[27] LIANG M, WANG R L, LI G X. Study of decomposition based on full-waveform lidar data[J]. Geomatics World, 2016, 23(5):51-54(in Chinese).
-
期刊类型引用(17)
1. 查冰婷,徐光博,秦建新,张合. 多发多收周视激光引信时刻鉴别方法. 兵工学报. 2024(11): 4145-4154 .  百度学术
百度学术
2. 熊丽丽,冯丽佳,苑柳青. 基于深度卷积神经网络的激光雷达图像轮廓线提取方法. 激光杂志. 2023(10): 94-99 .  百度学术
百度学术
3. 赵毅强,张琦,刘长龙,武唯康,李尧. 结合物理与几何特性的机载LiDAR数据分类方法. 红外与激光工程. 2023(11): 9-20 .  百度学术
百度学术
4. 贾权,郭计云,盛彬. 激光雷达硬件故障数据的模式识别研究. 激光杂志. 2022(04): 195-199 .  百度学术
百度学术
5. 唐春兰. 基于卷积神经网络的近红外光谱文本数据匹配检测方法. 激光杂志. 2022(10): 106-110 .  百度学术
百度学术
6. 赵炳炎,陈宗华,赵刘英. 基于Matlab的量子激光雷达稳频通信模拟系统设计. 激光杂志. 2021(02): 161-165 .  百度学术
百度学术
7. 韦复国,邱世平. 激光雷达技术在森林资源监测中的研究进展. 林业调查规划. 2021(01): 18-22+95 .  百度学术
百度学术
8. 翟宇,韩绍坤,李孟瑶,孟宪童,李俊. 基于全波形采样的APD阵列激光雷达系统研究. 光学技术. 2021(02): 149-154 .  百度学术
百度学术
9. 宫海晓,贺杰,杨秋慧. 机载激光雷达扫描三维地形的渲染研究. 激光杂志. 2021(04): 179-182 .  百度学术
百度学术
10. 富帅,倪建军,闫静纯,于双江,刘涛. 基于时钟网络的高速数据采集与处理系统设计. 太赫兹科学与电子信息学报. 2021(02): 228-234 .  百度学术
百度学术
11. 蒋心学,唐飞笼,杨迪. 机载三维激光点云数据分类数学模型. 激光杂志. 2021(07): 142-146 .  百度学术
百度学术
12. 闫晶,连婷,林海霞. 合成孔径激光雷达的目标重构方法. 激光杂志. 2021(07): 176-179 .  百度学术
百度学术
13. 王欣,翟羽婷,史春燕. 基于光纤耦合的RDF数据差异性检测系统设计. 激光杂志. 2021(11): 139-143 .  百度学术
百度学术
14. 奚东升,郭建勋,薛飞. 基于激光雷达扫描的输电空间三维数据协同方法. 电子设计工程. 2020(24): 57-60+65 .  百度学术
百度学术
15. 崔健. 基于机载激光雷达的树木倒伏隐患分析. 环境技术. 2020(06): 191-195 .  百度学术
百度学术
16. 苑宁萍,宁鹏飞. 海量激光传感器数据的自适应无损压缩研究. 激光杂志. 2019(10): 143-146 .  百度学术
百度学术
17. 丁征凯. 机载激光雷达数据在输电线路终勘选线中的运用分析. 通讯世界. 2018(09): 193-194 .  百度学术
百度学术
其他类型引用(6)



 下载:
下载: