网站地图
下载:
-
近年来，移频反馈激光器(frequency shifted feedback, FSF)以其独特的时频特性，被研究应用在锁模激光、激光线宽测量[3]、泰伯效应[4]、实时光域傅里叶变换[5]、啁啾[6]等诸多方向。移频反馈激光通常是在常规F-P腔[7-9]或者环形腔[10-12]内加入移频器(如声光调制器)，激光每次通过其都会发生频率的改变。通过控制反馈环路的增益，该激光可以输出多次移频后的拍频信号，其频率间隔由移频器的调制频率决定。当移频器的调制频率与反馈腔长满足一定关系时可以产生类似锁模体制的超短脉冲[13-20]。
作者通过在光纤环路中插入光纤放大器与声光调制器，设计出一种基于声光移频和光纤放大的频移反馈激光。通过注入1064nm波长的单频激光，在环路中实现了基频的拓展，通过控制光纤放大器(或增益)，研究了增益对各阶次谐波相对强度的影响。同时，建立了激光外差相干理论模型，通过耦合器传输效率矩阵对实验进行理论分析，推导出受放大增益系数影响的输出电场公式。最后，实验验证了放大增益系数对频谱中各阶次谐波相对强度的影响。
-
采用声光调制-光纤放大的光纤环路移频反馈激光器实验装置如图 1所示。该装置由连续激光器、声光调制器(acousto-optic modulation，AOM)、光纤放大器(ytterbium-doped fiber amplifier，YDFA)、光探测器、2×2光纤耦合器组成。波长为1064nm连续激光由输入端1注入2×2光纤耦合器，经由输出端口2输入声光调制器，声光调制器调制频率fAO，入射的激光经由声光调制器发生+1级衍射，衍射光由光纤放大器放大后，再经由输入端口2进入耦合器，部分光由输出端口2输出，端口2接探测器进行探测。输出端口1与输入端口2间形成环路，激光不断在环路中发生频移调制，由端口2输出频率间隔一致(fAO)的移频反馈激光，即实现了光学频率梳。
Figure 1. Experiment device of fiber loop frequency-shifted feedback lasers of acousto-optic modulate and fiber amplification(CW laser—continuous wave laser; AOFS—acousto-optic shifter)
-
设矩阵[tij]是耦合器的分光比，tij为其矩阵元，Ein是输入的电场，Eout是输出的电场，则输入的电场Ein与输出的电场Eout之间满足公式：
$ \left[ \begin{array}{l} {E_{{\rm{out, }}1}}\\ {E_{{\rm{out, 2}}}} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{t_{11}}}&{{t_{12}}}\\ {{t_{21}}}&{{t_{22}}} \end{array}} \right]\left[ \begin{array}{l} {E_{{\rm{in, 1}}}}\\ {E_{{\rm{in, }}2}} \end{array} \right] $
(1) 因为光纤组成一个闭合环路，则环路入射到耦合器的光场满足公式:
$ {E_{{\rm{in, 2}}}}(t) = \gamma {E_{{\rm{out, 2}}}}(t - \tau ){\rm{exp}}\left[ {{\rm{i2 \mathsf{ π} }}{f_{{\rm{AO}}}}\left( {t - \tau } \right)} \right] $
(2) 式中，t为时间变量，τ为光在环路中循环一次的时间，γ为表示频移、放大、相位偏置因素共同影响的复数。若设η为声光移频器的衍射系数，G为放大器的强度增益参量，φ为相位参量，则$ \gamma = \sqrt {\eta G} {{\rm{e}}^{{\rm{i}}\varphi }}$。其中φ为常量，通过调整初始的时间值，φ值可调为0。
由(1)式可以得到：
$ {E_{{\rm{out, 2}}}}\left( t \right) = {t_{12}}{E_{{\rm{in, 1}}}}(t) + {t_{22}}{E_{{\rm{in, }}2}}(t) $
(3) 将(2)式代入(3)式，则可得：
$ \begin{array}{l} {E_{{\rm{out, 2}}}}(t) = {t_{21}}{E_{{\rm{in, 1}}}}(t) + \\ {t_{22}}\gamma {E_{{\rm{out, 2}}}}(t - \tau ){\rm{exp}}\left[ {{\rm{i2 \mathsf{ π} }}{f_{{\rm{AO}}}}\left( {t - \tau } \right)} \right] \end{array} $
(4) 公式展开如下：
$ \left\{ \begin{array}{l} {E_{{\rm{out, 2}}}}\left( {t - \tau } \right) = {t_{21}}{E_{{\rm{in, 1}}}}(t - \tau ) + {t_{22}}\gamma {E_{{\rm{out, 2}}}}\left( {t-2\tau } \right) \times \\ {\rm{exp}}\left[ {{\rm{i2 \mathsf{ π} }}{f_{{\rm{AO}}}}\left( {t - 2\tau } \right)} \right]\\ {E_{{\rm{out, 2}}}}(t - 2\tau ) = {t_{21}}{E_{{\rm{in, 1}}}}\left( {t - 2\tau } \right) + {t_{22}}\gamma {E_{{\rm{out, 2}}}}(t - 3\tau ) \times \\ {\rm{exp}}\left[ {{\rm{i2 \mathsf{ π} }}{f_{{\rm{AO}}}}\left( {t - 3\tau } \right)} \right] \end{array} \right. $
(5) 将(5)式代入(4)式，可得:
$ \begin{array}{l} {E_{{\rm{out, 2}}}}\left( t \right) = {t_{21}}{E_{{\rm{in, 1}}}}(t) + \\ {t_{21}}{t_{22}}\gamma {E_{{\rm{in, 1}}}}(t - \tau ){\rm{exp}}\left[ {{\rm{i2 \mathsf{ π} }}{f_{{\rm{AO}}}}\left( {t - \tau } \right)} \right] + \\ {t_{21}}{({t_{22}}\gamma )^2}{E_{{\rm{in, 1}}}}(t - 2\tau ){\rm{exp}}\left[ {{\rm{i2 \mathsf{ π} }}{f_{{\rm{AO}}}}\left( {t - 2\tau } \right)} \right] + \\ {t_{21}}{({t_{22}}\gamma )^3}{E_{{\rm{in, 1}}}}(t - 3\tau ){\rm{exp}}\left[ {{\rm{i2 \mathsf{ π} }}{f_{{\rm{AO}}}}\left( {t - 3\tau } \right)} \right] + \\ \ldots \end{array} $
(6) (6) 式整理可得：
$ \begin{array}{l} {E_{{\rm{out, 2}}}}\left( t \right) = {t_{21}}\sum\limits_{p = 0}^\infty {} {\left( {{t_{22}}\gamma } \right)^p}{E_{{\rm{in, 1}}}}(t - p\tau ) \times \\ {\rm{exp}}\left[ {{\rm{i2 \mathsf{ π} }}{f_{{\rm{AO}}}}p\left( {t - \tau } \right)} \right]{\rm{exp}}\left[ {{\rm{i2 \mathsf{ π} }}{f_{{\rm{AO}}}}{p^2}t} \right] \end{array} $
(7) 实验中需要对输出端1的输出电场进行探测，即Eout, 1，且由于输入端1的输入电场Ein, 1易于测量。根据(2)式和(7)式，Eout, 1(t)可写为：
$ \begin{array}{l} {E_{{\rm{out, }}1}}\left( t \right) = {t_{11}}{E_{{\rm{in, 1}}}}(t) + {t_{12}}{E_{{\rm{in, 2}}}}\left( t \right) = {t_{11}}{E_{{\rm{in, 1}}}}\left( t \right) + \\ {t_{12}}\gamma {E_{{\rm{out, 2}}}}(t - \tau ){\rm{exp}}\left[ {{\rm{i2 \mathsf{ π} }}{f_{{\rm{AO}}}}\left( {t - \tau } \right)} \right] \end{array} $
(8) 如果入射电场Ein, 1为连续波，其能量为Pin，则满足:
$ \begin{array}{l} {E_{{\rm{out, }}1}}(t) = \left\{ {} \right.{\rm{ }}{t_{11}} + {t_{12}}\gamma {t_{21}}\sum\limits_{p = 0}^\infty {} {\left( {{t_{22}}\gamma } \right)^p} \times \\ {\rm{exp}}\left[ {{\rm{i2 \mathsf{ π} }}{f_{{\rm{AO}}}}\left( {p + 1} \right)\left( {t - \tau } \right)} \right] \times \\ {\rm{exp}}\left[ {{\rm{-i2 \mathsf{ π} }}{f_{{\rm{AO}}}}{p^2}t} \right]\left. {} \right\}\sqrt {{\rm{ }}{P_{{\rm{in}}}}} \end{array} $
(9) 式中, tij满足关系Tij=|tij|2，Tij为耦合器的光强传输系数，实验测得。
-
当入射激光器功率为40mW、声光调制器调制频率为200MHz、光纤环路光程约为27.90m、光纤放大器的输出功率为30mW时，移频反馈激光的拍频功率谱分别如图 2a所示，其频谱由一串频率间隔相同的谐波组成，相邻谐波的频率间隔为200MHz, 最高阶谐波频率为2.4GHz。
Figure 2. Relationship between power spectral density and frequency under different powers
为了研究不同增益系数(即参量G)对频谱中各谐波强度和最高阶谐波的影响，调节光纤放大器的输出功率分别为50mW，70mW，80mW, 其功率谱如图 2b~图 2d所示。随着输出功率的增大，最高阶谐波的频率也随着提高。同时可以发现，部分谐波存在着明显的抑制现象，即均低于左右两边的谐波，这是由于反馈腔内激光干涉时的相互抵消导致。
-
由于实验中采用光纤放大器的输出功率为控制参量，为了更加深入的研究频移反馈激光的相关特性，理论中采用更为普遍的增益系数G作为控制变量，数值仿真增益系数G对拍频频谱的影响。当G分别取值G=1.6，G=2.4，G=2.6，G=2.8时，功率频谱密度如图 3a~图 3d所示。通过对比可以发现，实验与仿真结果相吻合，具有较高一致性。同时由图 3a~图 3d对比可以观察，随着G的不断增大，各阶次谐波的强度也发生了较大的变化; 增益系数越大，最高阶的谐波阶次也越高。因此，光纤放大器的引入有效地实现了基频的拓展，为实现信号的频谱上变换提供了一种有效的方法。除此之外，各阶次频率的相对强度也具有一定规律。以1GHz拍频为例，从图中可以明显发现其强度明显低于左右两边谐波的高度，这是由于激光在反馈腔内外差干涉时的相互抵消作用，尤其表现在当G=4时，1GHz整数倍的谐波明显低于左右两边。同时，受探测器的最大带宽3.5GHz的限制，实验中无法观察到更高阶次的谐波。
Figure 3. Relationship between power spectral density and frequency under different power gain G
-
通过声光调制-光纤放大的光纤环路，得到了一个不断移频放大的频率梳式激光器，并对其理论进行了研究。吻合较好的实验及仿真结果说明，光纤放大器的增益对频谱图的波形具有一定的影响。后续的实验若能通过选择性能更优越的探测器或在实验装置中添加衰减元件来解决探测器峰值功率及其增益带宽的问题，对移频反馈激光器的选频问题则具有一定的意义。
光纤环路移频反馈激光器及放大器增益的研究
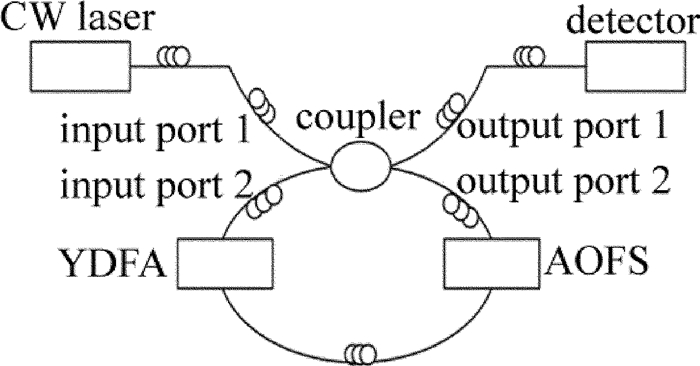
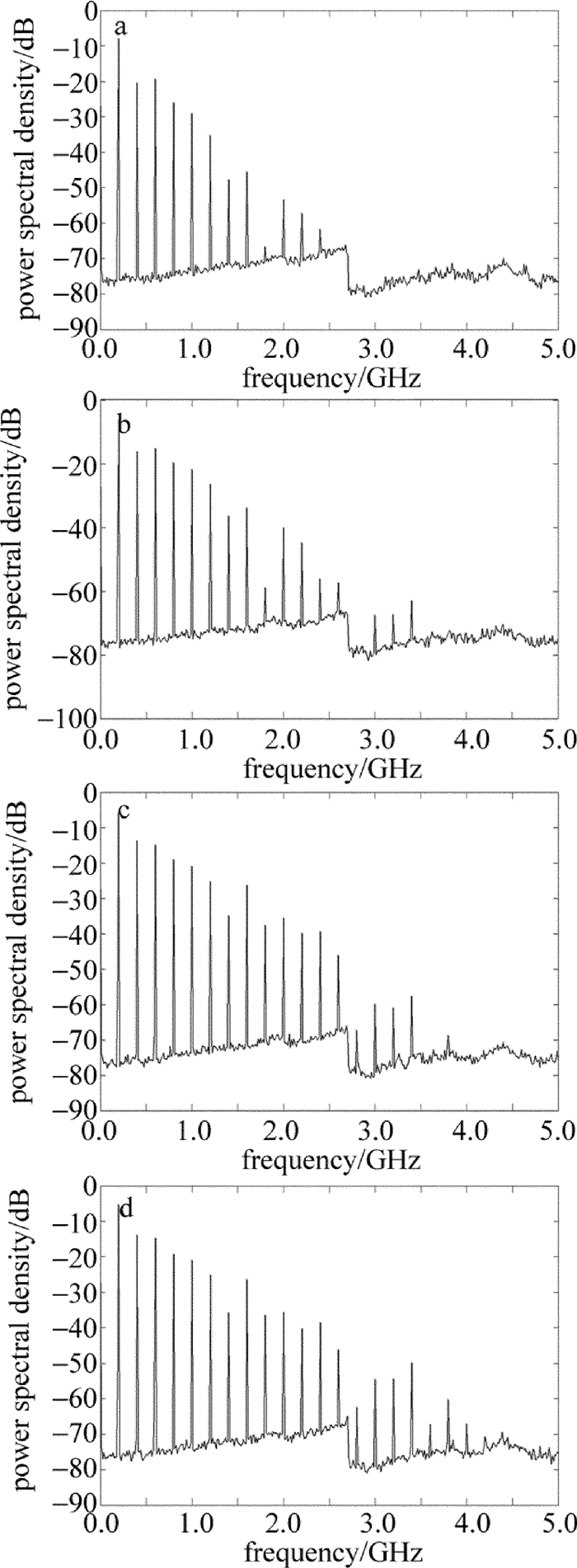
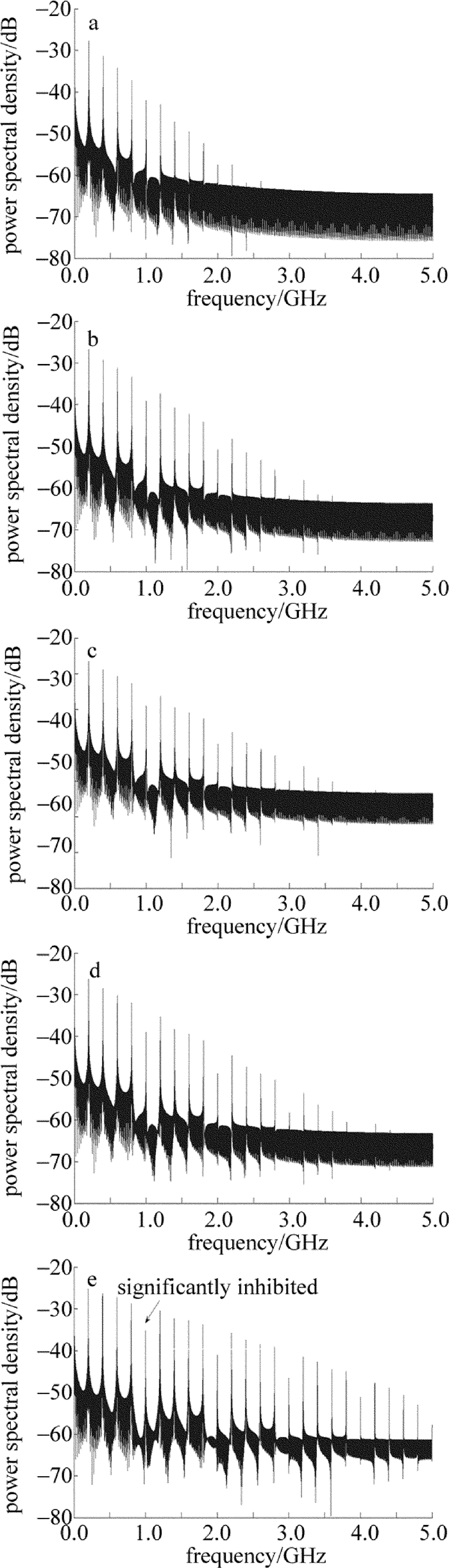
Research of frequency-shifted feedback laser based on fiber loop and amplifier gain
-
摘要: 基于声光调制的频移反馈激光器是目前研究的热点，它可以生成一串频率间隔相同的谐波。为了生成多频激光，采用移频反馈激光器的方法，设计了一种全光纤式移频-放大反馈环路，建立了基于频移反馈腔的激光外差相关理论模型，并进行了数值仿真。同时，在环路中引入光纤放大器，研究了增益系数对各阶次谐波相应强度的影响，验证了不同增益系数对各阶次频率的选择作用。结果表明，利用频移反馈回路，实现了数倍于基频的高频调制，最高调制频率可达4GHz。这为新体制高频调制激光的研究奠定了理论及实验基础。Abstract: Frequency-shifted feedback laser based on acousto-optic modulation was one research hotspot in the current, and it can produce a string of harmonic wave with same interval frequency. In order to generate multi-frequency laser, the frequency-shifted feedback laser method was adopted to design an all-fiber frequency-shifted amplified feedback loop. A theoretical model of laser heterodyne correlation was established and the numerical simulation was carried out. At the same time, a fiber amplifier was introduced into the loop, and the influence of gain coefficient on the corresponding intensity of each harmonic was studied. The selection of different gain parameters for each order frequency was verified. The results show that, frequency-shifted feedback loop could be used to achieve the high-frequency modulation, several times of the fundamental frequency modulation. The highest modulation frequency is up to 4GHz. The study lays the theoretical and experimental foundation for the research of the new system of high-frequency modulation laser.
-
Key words:
- lasers /
- frequency shifted feedback laser /
- acousto-optic modulate /
- fiber amplifier
-
Figure 1. Experiment device of fiber loop frequency-shifted feedback lasers of acousto-optic modulate and fiber amplification(CW laser—continuous wave laser; AOFS—acousto-optic shifter)
Figure 2. Relationship between power spectral density and frequency under different powers
a—30mW b—50mW c—70mW d—80mW
-
[1] RYU H Y, MOON H S, SUH H S. Optical frequency comb generator based on actively mode-locked fiber ring laser using an acousto-optic modulator with injection-seeding[J]. Optics Express, 2007, 15(18):11396-11401. doi: 10.1364/OE.15.011396 [2] YOSHIDA M, FUJIMOTO M, NAKAZAWA M, et al. A mode-locked frequency-shifted feedback fiber lasers[C]//Coference on Lasers and Electro-Optics, 2001. New York, USA: IEEE, 2001: 299-300. [3] HALE P D, KOWALSKI F V. Output characterization of a frequency shifted laser:Theory and experiment[J]. Journal of Quantum Electronics, 1990, 10(10):1845-1851. [4] BERRY M V, KLEIN S. Integer, fractional and fractal Talbot effects[J]. Journal of Modern Optics, 1996, 43(10):2139-2164. doi: 10.1080/09500349608232876 [5] de CHATELLUS H G, PIQUE J P. Statistical properties of frequency shifted feedback lasers[J]. Optics Communications, 2010, 283(1):71-77. doi: 10.1016/j.optcom.2009.09.027 [6] YATSENKO L P, SHORE B W, BERGMANN K. Theory of a frequency-shifted feedback laser[J]. Optics Communications, 2004, 236(1/3):183-202 [7] ZHANG H Y, BRUNEL M, ROMANELLI M, et al. Green pulsed lidar-radar emitter based on a multipass frequency-shifting external cavity[J]. Applied Optics, 2016, 55(10):2467-2473. doi: 10.1364/AO.55.002467 [8] VALLET M, BARREAUX J, ROMANELLI M, et al. Lidar-radar velocimetry using a pulse-to-pulse coherent RF-modulated Q-switched laser[J]. Applied Optics, 2013, 52(22):5402-5410. doi: 10.1364/AO.52.005402 [9] HEIDT V, BURGER J P, MARAN J N.High power and high energy ultrashort pulse generation with a frequency shifted feedback fiber laser[J]. Optics Express, 2007, 15(24):15892-15897. doi: 10.1364/OE.15.015892 [10] SABERT H, BRINKMEYER E. Pulse generation in fiber lasers with frequency shifted feedback[J]. Journal of Lightwave Technology, 1994, 12(8):1360-1368. doi: 10.1109/50.317522 [11] NIKODEM M P, KLUZNIAK E, ABRAMASKI K. Wavelength tenability and pulse duration control in frequency shifted feedback re-doped fiber lasers[J]. Optics Express, 2009, 17(5):3299-3304. doi: 10.1364/OE.17.003299 [12] NAKAMURA K, HARA T, YOSHIDA M, et al. Optical frequency domain ranging by a frequencyshifted feedback laser[J]. IEEE Journal of Quantum Electronics, 2000, 36(3):305-316. doi: 10.1109/3.825877 [13] KOWALSKI F V, NDIAYE C, NAKAMURA K. Noise waveforms with repetitive phase and nonrepetitive amplitude[J]. Optics Letters, 2002, 27(22):1965-1967. doi: 10.1364/OL.27.001965 [14] YATSENKO L P, SHORE B W, BERGMANN K. Coherence in the output spectrum of frequency shifted feedback lasers[J]. Optics Communications, 2009, 282(2):300-309. doi: 10.1016/j.optcom.2008.10.002 [15] KOWALSKI F V, SQUIER J A, PINCKNEY J T. Pulse generation with an acousto-optic frequency shifter in a passive cavity[J]. Applied Physics Letters, 1987, 50(12):711-713. doi: 10.1063/1.98075 [16] de CHATELLUS H G, JACQUIN O, HUGON O, et al. Generation of ultrahigh and tunable repetition rates in CW injection-seeded frequency-shifted feedback lasers[J]. Optics Express, 2003, 21(13):15065-15074. [17] KOWALSKI F V, NDIAYE C, NAKAMURA K. Noise waveforms generated by frequency shifted feedback lasers:application to multiple access communications[J]. Optics Communications, 2016, 231(1/6):149-164. [18] NIKODEM M, ABRAMSKI K. Controlling the frequency of the frequency shifted feedback fiber laser using injection-seeding technique[J]. Optics Communications, 2010, 283(10):2202-2205. doi: 10.1016/j.optcom.2010.01.030 [19] PHILLIPS M W, LIANG G Y, BARR J R M. Frequency comb generation and pulsed operation in a Nd:YAG laser with frequency-shifted feedback[J]. Optics Communications, 1993, 100(5/6):473-478. [20] COPPIN P, HODGKINSON T G. Novel optical frequency comb synthesis using optical feedback[J]. Electronics Letters, 1990, 26(1):28-30. -
点击查看大图
图(3)
计量
- 文章访问数: 9299
- HTML全文浏览量: 6947
- PDF下载量: 252
- 被引次数: 0
