网站地图
-
随着工业和能源技术不断发展，太阳能逐渐被人类所利用。相较于传统Si太阳电池，GaAs太阳电池具有光电转换效率高、抗辐射性能强等优点，在航空航天方面有广阔的潜在价值和应用背景[1-5]。激光辐照下三结GaAs太阳电池由于材料热吸收引起电池热效应，从而影响其输出性能降低[6]，因此仿真计算出连续激光辐照三结GaAs太阳电池温度场极具科学意义，可以为激光辐照太阳电池致损伤现象提供理论依据。近些年，国内外学者对于连续激光辐照太阳电池研究极其关注，国外研究方向主要为激光无线传输。2002年，德国STEINSIEK[7]等人利用532nm激光成功驱动了小车。2005年，美国马歇尔空间飞行中心利用500W强激光辐照15m以外微型飞行器表面的GaInP2光伏电池，成功让飞行器飞行。2006年，日本近畿大学采用激光辐照装备GaAs光伏电池的风筝和微型直升机，实现了激光供能试验[9]。而国内侧重于连续激光辐照太阳电池损伤机理。2013年，QIU[10]等人采用1064nm连续激光辐照单晶Si太阳电池，通过对比辐照前后输出特性变化，分析了连续激光损伤单晶Si太阳电池机理。2017年，YANG[11]等人采用波长为1070nm连续激光，在真空环境下实验测量了不同功率密度激光作用三结GaAs太阳电池温度和负载电压的实时变化，得到了其太阳电池损伤阈值为11.7W/cm2。但是目前对于连续激光辐照GaAs太阳电池只有相关实验，很少有在考虑材料热物性参量随温度变化情况下，通过同时构建光电转换和光热转换理论模型来求解太阳电池温度场。
本文中利用COMSOL仿真软件构建了1070nm连续激光辐照三结GaAs太阳电池的物理模型，通过有限元法求解了其热传导方程，得到了与实验结果基本相符的数值结果，进行了数值解与实验值的误差分析，并讨论了入射激光功率密度、光斑半径、减反膜和热辐射热对流对温度场的影响。
-
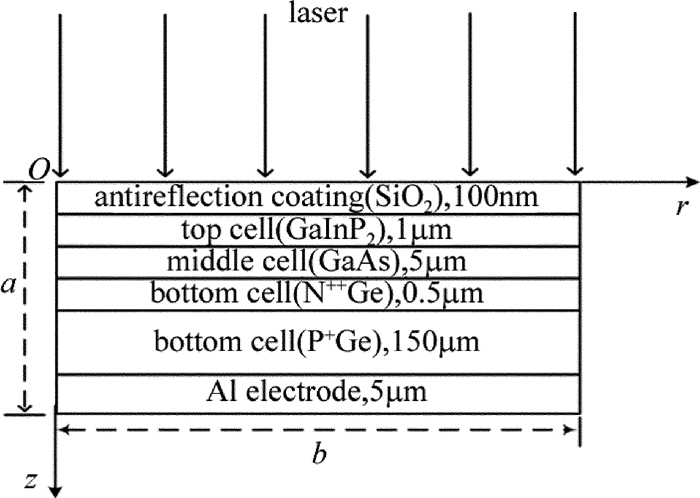
1070nm连续激光辐照三结GaInP2/GaAs/Ge太阳电池物理模型和各层尺寸如图 1所示。图中O为坐标原点，r方向表示太阳电池径向方向，z方向表示太阳电池轴向方向，a为太阳电池厚度，b为太阳电池半径。
Figure 1. 2-D axisymmetric model of solar cell at 1070nm continuous wave laser irradiation
当激光辐照到太阳电池时，经电池表面反射，透射到底电池的激光能量一部分传给光生载流子，通过电池内建场作用在底电池P-N结薄层之间产生光生伏打电动势，剩余部分则以声子形式传递给晶格转换为热能积聚在电池内部。因此通过求解光电转换模型中太阳电池转换效率，其剩余激光能量全部转换为热量作为光热转换模型中电池热源项。
-
基于P-N结整流方程，太阳电池理想模型中各电学参量方程式[12]为：
$ {V_{{\rm{OC}}}} = \frac{{A{k_{\rm{B}}}T}}{q}\ln \left( {\frac{{{I_{{\rm{ph}}}}}}{{{I_{\rm{s}}}}} + 1} \right) $
(1) $ {I_{{\rm{SC}}}} = {I_{{\rm{ph}}}} $
(2) $ \eta = \frac{{{I_{{\rm{SC}}}}{V_{{\rm{OC}}}}{F_{\rm{f}}}}}{{{P_{{\rm{in}}}}}} $
(3) $ {F_{\rm{f}}} = \frac{{{V_{{\rm{OC,n}}}} - \ln \left( {{V_{{\rm{OC,n}}}} + 0.72} \right)}}{{{V_{{\rm{OC,n}}}} + 1}} $
(4) $ {V_{{\rm{OC,n}}}} = \frac{{{V_{{\rm{OC}}}}}}{{{k_{\rm{B}}}T/q}} $
(5) 式中, ISC和VOC分别为太阳电池短路电流和开路电压；Iph为光生电流，Is为反向饱和电流；Pin为入射激光功率；η为光电转换效率；A为二极管理想因子；kB为玻尔兹曼常数；q为电子电量；Ff为填充因子；VOC,n为归一化开路电压。
$ {I_{\rm{s}}} \approx Sq\left[ {{D_{\rm{n}}}n_{\rm{i}}^2/\left( {{L_{\rm{n}}}{N_{\rm{a}}}} \right) + {D_{\rm{p}}}n_{\rm{i}}^2/\left( {{L_{\rm{p}}}{N_{\rm{d}}}} \right)} \right] $
(6) $ \left\{ \begin{array}{l} {D_{\rm{n}}} = {k_{\rm{B}}}T{\mu _{\rm{n}}}/q\\ {D_{\rm{p}}} = {k_{\rm{B}}}T{\mu _{\rm{p}}}/q \end{array} \right. $
(7) $ {I_{{\rm{SC}}}} = \left( {1 - R} \right){P_{{\rm{in}}}}{Q_{\rm{e}}}\left( T \right)\frac{\lambda }{{1240}} $
(8) $ {Q_{\rm{e}}}\left( T \right) = {Q_{\rm{e}}}\left( {{T_0}} \right)\left[ {1 + {k_1}\left( {T - {T_0}} \right)} \right] $
(9) 式中, S为光斑面积；Dn和Dp分布为电子和空穴扩散系数；Ln和Lp分别为电子和空穴扩散长度；ni为Ge本征载流子浓度；Na和Nd分别为底电池P-N结两侧受主掺杂浓度和施主掺杂浓度；μn和μp分别为电子和空穴迁移率；R为电池表面反射率；λ为入射激光波长；Qe(T)为内量子效率；Qe(T0)为室温T0下内量子效率；kt为内量子效率温度系数。表 1中给出了光电转换模型中各种参量[15-16]。
Table 1. Parameters of photoelectric conversion model
parameter value the Boltzmann constant kB/(J·K－1) 1.381×10－23 unit charge q/C 1.6×10－19 diode ideal factory A 2 intrinsic carrier concentration ni/cm-3 9.15×1019 (T/300)1.5×exp[－15.2/(T/300)] internal quantum efficiency at T0 Qe(T0) 0.95 internal quantum temperature coefficient kt 8×10－4 reflectivity R 0.1 laser wavelength λ/nm 1070 electron mobility μn/(cm2·V-1·s-1) 4000×(T/300)－2.5 hole mobility μp/(cm2·V-1·s-1) 2090×(T/300)－2.33 electron diffusion length Ln/μm 1.5 hole diffusion length Lp/μm 3 acceptor doping concentration Na/cm-3 1×1017 donor doping concentration Nd/cm-3 1×1018 -
柱坐标系下热传导方程为：
$ \begin{array}{*{20}{c}} {{\rho _m}{c_m}\frac{{\partial {T_m}\left( {r,z,t} \right)}}{{\partial t}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left[ {r{\kappa _m}\frac{{\partial {T_m}\left( {r,z,t} \right)}}{{\partial r}}} \right] + }\\ {\frac{\partial }{{\partial z}}\left[ {{\kappa _m}\frac{{\partial {T_m}\left( {r,z,t} \right)}}{{\partial z}}} \right] + {Q_m}\left( {T,r,z,t} \right)} \end{array} $
(10) 式中, m=1, 2, 3, …；Tm(r, z, t)，ρm，cm和κm表示在t时刻的第m层温度场分布、材料密度、比热容和热导率；Qm(T, r, z, t)为在第m层材料中的激光功率体密度。
由于减反膜层、顶电池层GaInP2和中电池层GaAs对波长1070nm激光吸收系数非常小，可假设其不吸收此波长光能。在300K~400K时，Ge对1070nm波长激光吸收系数约为13600cm-1~15100cm-1[16]，其穿透深度为几个微米，因此太阳电池热源可设为底电池层吸收热源Q(T, r, z, t)：
$ \begin{array}{*{20}{c}} {Q\left( {T,r,z,t} \right) = {I_0}\left( {1 - R - \eta } \right)\alpha \left( T \right)f\left( r \right)g\left( t \right) \times }\\ {\exp \left[ { - \alpha \left( T \right)z} \right],\left( {0{\rm{ \mathsf{ μ} m}} < z \le 4.5{\rm{ \mathsf{ μ} m}}} \right)} \end{array} $
(11) $ \left\{ \begin{array}{l} f\left( r \right) = \left\{ \begin{array}{l} \exp \left( { - 2{r^2}/a_0^2} \right),\left( {0 < r \le {a_0}} \right)\\ 0,\left( {r > {a_0}} \right) \end{array} \right.\\ g\left( t \right) = 1,\left( {0 < t \le \infty } \right) \end{array} \right. $
(12) 式中, I0为激光功率密度；f(r)和g(t)分别是入射激光能量空间分布和时间分布；a0为入射激光光斑半径；α(T)为Ge对入射激光吸收系数。
由于实验[11]中使用的真空泵能够达到最低真空度为10-4Pa，不能使太阳电池处于绝对真空环境，因此对该物理模型加入热对流修正，则初始条件和边界条件为：
$ T\left( {r,z,t} \right)\left| {_{t = 0}} \right. = {T_0} = 300{\rm{K}} $
(13) $ - \kappa \frac{{\partial T{{\left( {r,z,t} \right)}_{t = 0}}}}{{\partial z}}\left| {_{z = a}} \right. = - \kappa \frac{{\partial T\left( {r,z,t} \right)}}{{\partial r}}\left| {_{r = b}} \right. = 0 $
(14) $ \begin{array}{*{20}{c}} { - \kappa \frac{{\partial T\left( {r,z,t} \right)}}{{\partial z}}\left| {_{z = 0}} \right. = - h\left[ {T\left( {r,z,t} \right) - {T_0}} \right] - }\\ {\sigma \varepsilon \left[ {{T^4}\left( {r,z,t} \right) - T_0^4} \right]} \end{array} $
(15) 式中, T0为环境温度；κ为Ge的热导率；σ为斯特藩常量；h为热对流系数；ε为电池上表面发射率；T(r, z, t)为电池表面温度。表 2中给出了Ge材料热学参量[16]。
Table 2. Thermal parameters of Ge
parameter value density ρ /(kg·m-3) 5323.4 thermal conductivity κ /(W·cm-1·K-1) 0.6×(T /300)－1 specific heat capacity c /(J·kg-1·K-1) 303+6.13×10－2T energy gap Eg/eV 0.803－3.9×10－4T coefficient of heat transfer h /(W·m-2·K) 10 the Stefan constant σ /(W·m-2·K-4) 5.67×10－8 thermal radiation rate ε 0.1 laser radius a0/cm 1.5 cell radius b /cm 1.5 absorption coefficient α(T)/cm-1 1.4×104exp[2.81×(1.16+0.67－Eg－1.17)] -
基于三结GaAs太阳电池理想模型，利用COMSOL软件根据上述物理模型数值计算5W/cm2激光功率密度辐照下，1070nm连续激光辐照三结GaAs太阳电池温度场分布，且与实验值[11]进行对比，激光与太阳电池作用时间为20s。
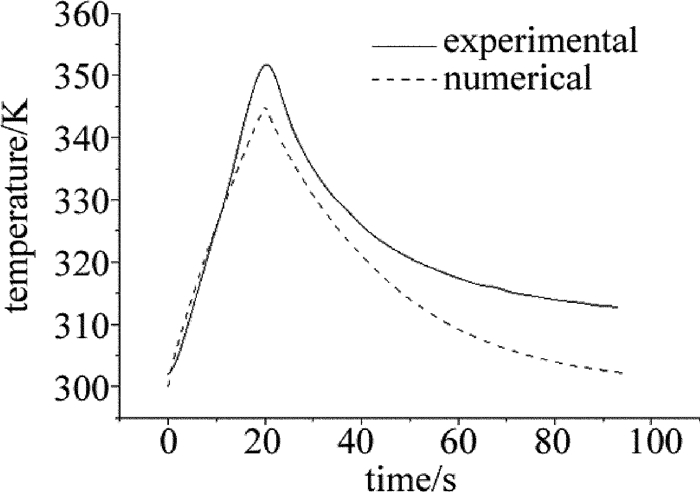
图 2中是5W/cm2功率密度辐照下，电池中心温度实验值[11]和数值解对比曲线。从图 2可见, 数值解曲线变化趋势大致和实验值相同，在激光作用的时间(小于20s)内，电池中心温度随时间上升，且在激光作用结束时刻(20s)出现温度最大值，随后温度开始下降。但在激光作用电池结束，即20s时刻，太阳电池最高温度且其后的温降曲线数值解比实验值略高，其主要原因有两个：(1)(15)式中设电池周围环境温度是室温恒定，但电池处于狭小封闭的真空腔中，其周围热量较难散去，降低了电池对外热辐射热对流能力，因此加剧了温度的升高；(2)所构建模型未考虑实验中使用的模拟太阳光源卤钨灯对电池温升的贡献。实验[11]中当入射激光功率为11.7W/cm2时，电池中心温度达到了662K，而数值解只有426.74K，从而验证了误差分析的合理性。
Figure 2. Relationship between cell center temperature and time at power density of 5W/cm2
-
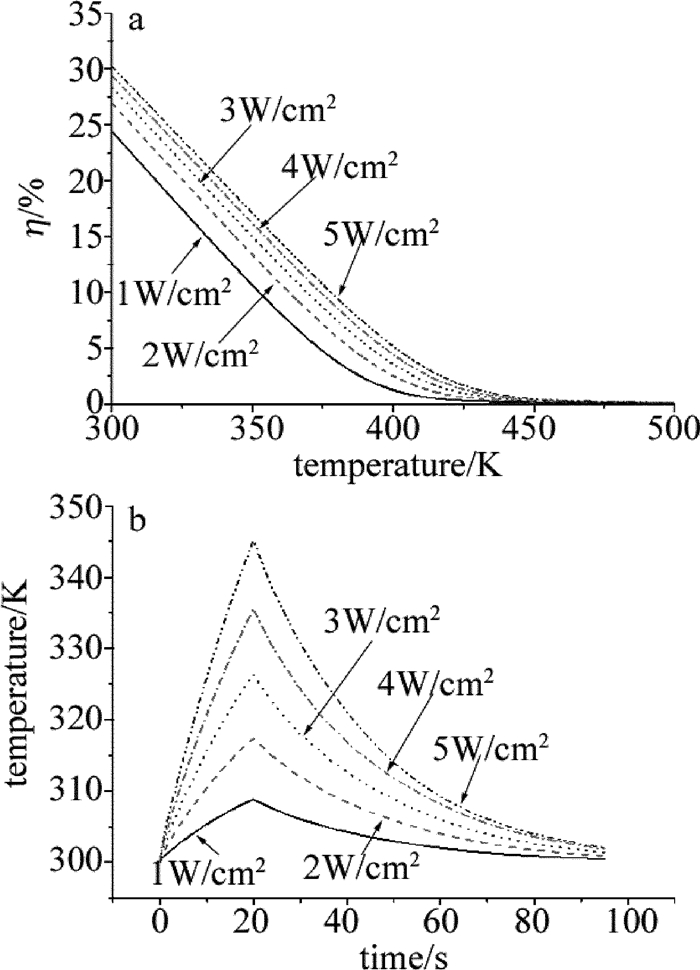
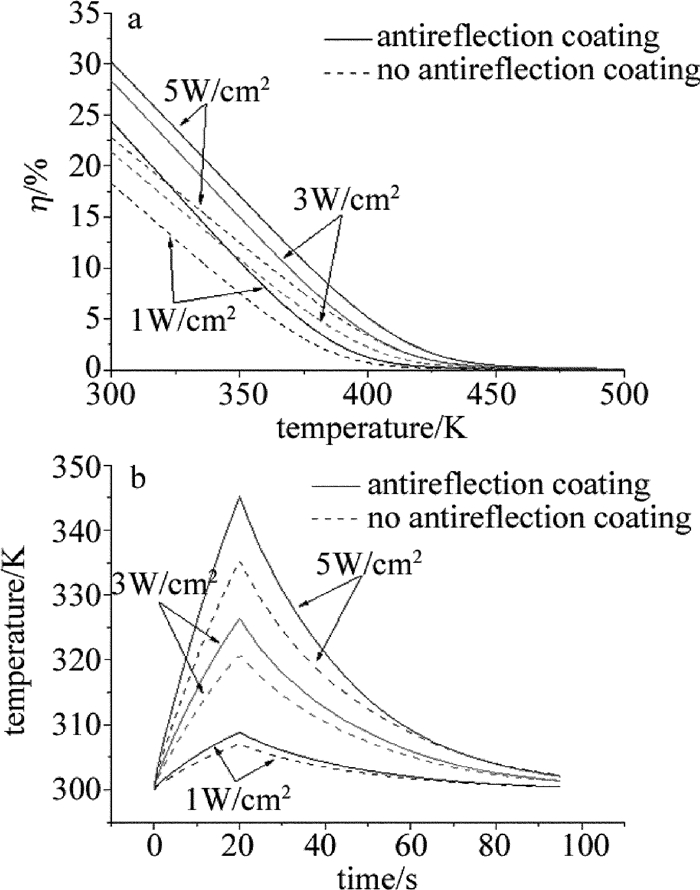
不同激光功率密度辐照下，光电转换效率和电池中心温度变化曲线如图 3所示。从图 3a可见, 光电转换效率会随功率密度的增加而增加，且其都随温升而降低，都在500K时光电转换效率下降为0，即对应三结GaAs太阳电池发生光伏效应的温度阈值。
Figure 3. a—relationship between photoelectric conversion efficiency and temperature at various power densities b—relationship between temperature change of cell center and time at various power densities
当激光功率密度增加，光电转换效率的提高减少了电池热量的积累，但由图 3b可见，功率密度增加导致电池吸收总能量的增加对电池温升起主要影响。因此不同功率密度对应的温升曲线其斜率会随功率密度的增加而增加，且在20s时刻会出现一个尖峰，达到温度最大值，随着时间延长，电池中心温度会不断降低。
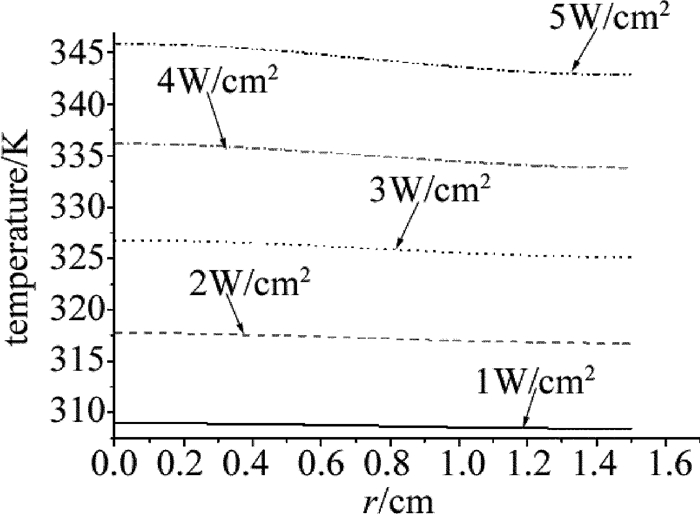
图 4表示不同激光功率密度辐照下，电池20s时刻径向温度分布曲线。由图 4可见, 随着功率密度增大，电池径向温度会减小，且径向温差绝对值随功率密度增大而增大。原因主要有两个：(1)GaAs和Ge材料吸收系数随着温度增加而不断增加，因此更多的激光能量被电池中心区域吸收，即激光能量越来越积聚在电池中心；(2)GaAs和Ge材料热传导系数随温度升高而不断减小，导致电池中心区域能量密度大，热量更难向径向扩散。
Figure 4. Relationship between radial temperature and radial length at 20s under various power densities
图 5表示16.7W/cm2激光功率密度辐照下，电池20s时刻轴向温度变化曲线。由图 5可看出，电池中心温度达到501.521K，此时已超过光电转换阈值温度，导致电池不能正常工作，而温度沿深度方向变化很小，即电池上下表面温差较小。主要物理原因是连续激光与材料作用过程中，电子吸收光能通过发射声子将能量传递给晶格，而晶格弛豫时间为飞秒量级(10-12s)，因此, 电子有足够的时间将能量向材料内部晶格传递形成有效的热传导。若用飞秒脉冲激光作用材料可知, 电子吸收能量至冷却这过程结束时间量级为10-12s，此时电子几乎没有时间将能量传递给晶格，即上下表面温度差将很大。
Figure 5. Relationship between axial temperature and axial length at 20s under power density of 16.7W/cm2
-
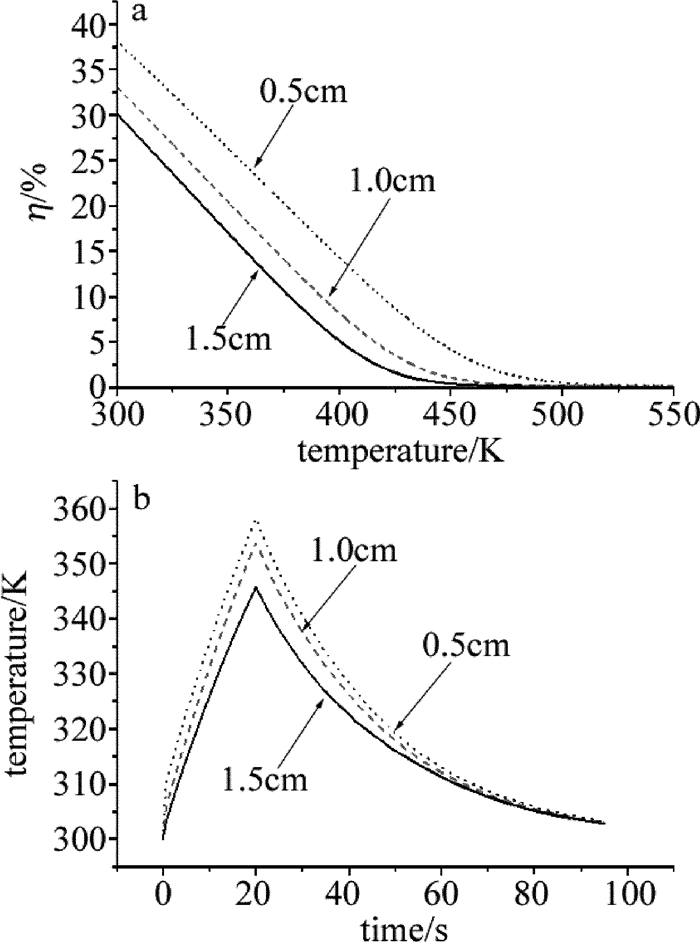
当入射激光功率为35W时，不同光斑半径辐照下光电转换效率和电池中心温度变化曲线如图 6所示。从图 6a可见，一方面随着入射光斑半径减小，光电转换效率明显提高，这是由于电池反向饱和电流会随光斑面积减小而减小，使得开路电压加大，导致效率升高，进而减少了热量在电池内部的积累。而另一方面, 辐照区域内功率密度随光斑半径减小而增大，引起电池温升较大。从图 6b可见, 后者所引起的温升效应占主导作用，电池中心温度随光斑半径减小而增加。
Figure 6. a—relationship between photoelectric conversion efficiency and temperature under various laser spot radius of input laser power 35W b—relationship between temperature change of cell center and time under various laser spot radius of input laser power 35W
由图 7可知，随着入射光斑半径越小，电池径向温差会越大。当入射光斑半径为0.5cm时，激光作用20s时刻，电池中心和边缘温差为15.14K，且其边缘温度小于1.0cm光斑半径辐照下温度。其主要原因是辐照区域温度随光斑半径减小而增加，进一步导致材料热传导系数变小和吸收系数变大，使得辐照区域热量更难向未辐照区域扩散。当电池表面温度差较大时, 可能使得太阳电池内部P-N结构发生热应力损伤，减小电池使用寿命，因此减小连续激光作用光斑半径可有效地损伤太阳电池。
Figure 7. Relationship between radial temperature and radial length at 20s under various laser spot radius of input laser power 35W
-
当激光入射到太阳电池表面时会产生反射，减少了太阳电池对激光能量的吸收。因此为提高激光能量利用率，在电池表面镀上一层减反射膜。该减反射膜可使1070nm激光的反射系数R从0.3减到0.1。
图 8为有无减反射膜时，光电转换效率和电池中心温度变化曲线。从图 8a可见，无减反膜时反射率的增大导致转换效率有明显降低。由(1)式、(2)式、(3)式可知，光电转换效率的降低是短路电流和开路电压共同减小的体现。而图 8b可以得到：有减反膜和无减反膜时, 连续激光辐照太阳电池引起温度变化趋势类似，但在相同入射功率密度作用下, 无减反膜时电池中心温度低于有减反膜时，这是因为无减反膜使得转换效率降低和电池表面反射率增加，一方面转换效率的降低导致电池将激光能量更多转换为热量，而另一方面表面反射率的增加却是导致相反的结果，由(11)式可看出, 表面反射率的增加引起激光能量损失占主导作用。而温升过程中材料吸收系数不断增大和热导率不断减小，有无减反膜所致温度差会随入射激光功率密度的增大而增大。因此, 在太阳电池表面镀上减反膜虽对光电转换效率的提升极其重要，但同时会使得太阳电池温度较高。
Figure 8. a—relationship between photoelectric conversion efficiency and temperature with and without antireflection coating b—relationship between temperature change of cell center and time with and without antireflection coating
-
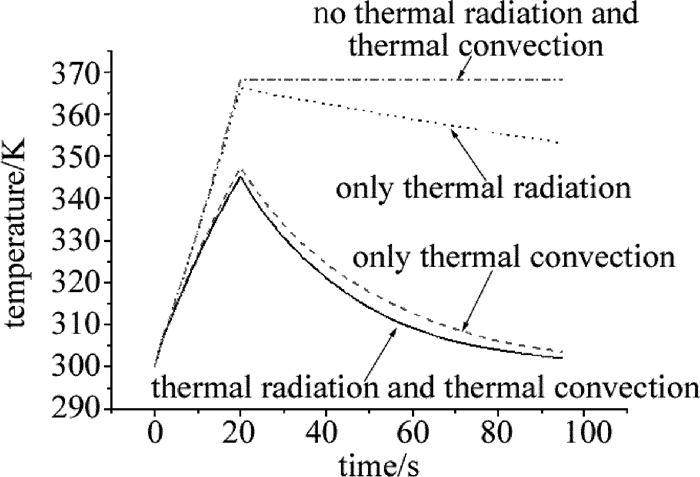
图 9中展示了热辐射热对流对太阳电池温度场分布的影响。其中4条曲线分别为:考虑热辐射热对流条件下电池中心温升曲线；只考虑热对流条件下电池中心温升曲线；只考虑热辐射条件下电池中心温升曲线；以及未考虑热辐射热对流条件下电池中心温升曲线。由图 9可见, 4种条件下温升变化趋势大致相同，但在温降过程中，由热对流项－h[T(r,z,t)－T0]和热辐射项－σε[T4(r,z,t)－T04]对比计算可知，在电池温度较低(300K~400K)情况下，热对流对于激光辐照电池过程中对外散热占据主导作用。因此，若在绝对真空环境下，由于不存在热对流散热，激光辐照下电池热量积累较快，温度会大幅上升，进而降低电池光电转换效率。
Figure 9. Relationship between temperature and time at power density of 5W/cm2
-
利用COMSOL软件、通过有限元法构建1070nm连续激光辐照三结GaAs太阳电池的物理模型，计算出5W/cm2入射激光功率密度辐照下电池的温度场分布，并对实验值和数值解进行对比，分析出误差存在的机理原因。此外讨论了入射激光功率密度、光斑半径、减反膜和热辐射热对流对温度场的影响：温升幅度随着激光功率密度的增大而增大；太阳电池表面温差会随着激光入射光斑半径减小而不断增大；拥有减反膜结构可有效地提高太阳电池转换效率，但也会升高电池温度；在电池温度较低(300K~400K)情况下，热对流对外散热占据主导作用。当入射功率密度为16.7W/cm2，光斑半径与电池半径相同时，经20s后，电池中心温度达到501.521K，导致光电转换效率为0。该数值解与实验值基本一致，可为激光损伤太阳电池机理研究提供一定的理论依据。
连续激光辐照三结GaAs太阳电池温度场仿真
Simulation of three-junction GaAs solar cell temperature field by continuous wave laser irradiation
-
摘要: 为了研究真空环境下1070nm连续激光辐照对三结GaAs太阳电池输出性能的影响，利用COMSOL软件构建了相应物理模型，通过数值仿真研究了激光功率密度、光斑半径、减反膜和热辐射热对流对温度场的影响。结果表明，吸收系数、热导率和光电转换效率是温度演变的3个主要因素；温升幅度随激光功率密度增大而增大；光斑半径越小使得电池表面温差越大；拥有减反膜结构可有效地提高太阳电池转换效率，但也使电池温度较高；热对流散热在电池较低温度（300K~400K）情况下占据主导作用；当入射功率密度为16.7W/cm2、光斑半径与电池半径相同时，经20s后，电池中心温度达到501.521K，导致光电转换效率为0。该数值模拟结果与实验结果基本相符，对激光损伤太阳电池机理研究提供一定的理论依据。Abstract: In order to study the effects of 1070nm continuous wave laser irradiation on output performance of three-junction GaAs solar cell, a physical model was established by software COMSOL. The influence of laser power density, spot radius, anti reflection film, thermal radiation and thermal convection on temperature field were studied by numerical simulation. The results show that, absorption coefficient, thermal conductivity and photoelectric conversion efficiency are three main factors of temperature evolution. The magnitude of temperature increases with the increasing of laser power density. The smaller the spot radius is, the greater the temperature difference of cell surface. The conversion efficiency of solar cells can be effectively improved by anti reflection film structure, but it also makes battery temperature higher. Thermal convection dominates under the lower temperature (300K~400K) of the battery. When the incident power density is 16.7W/cm2 and spot radius is the same as the cell radius, after 20s, the central temperature of battery can reach 501.521K and lead to photoelectric conversion efficiency of 0. The numerical simulation results are in good agreement with the experimental results. The study provides a theoretical basis for the research of the mechanism of laser damage solar cells.
-
Key words:
- laser technique /
- continuous wave laser /
- numerical simulation /
- temperature field
-
Figure 1. 2-D axisymmetric model of solar cell at 1070nm continuous wave laser irradiation
Figure 2. Relationship between cell center temperature and time at power density of 5W/cm2
Figure 3. a—relationship between photoelectric conversion efficiency and temperature at various power densities b—relationship between temperature change of cell center and time at various power densities
Figure 4. Relationship between radial temperature and radial length at 20s under various power densities
Figure 5. Relationship between axial temperature and axial length at 20s under power density of 16.7W/cm2
Figure 6. a—relationship between photoelectric conversion efficiency and temperature under various laser spot radius of input laser power 35W b—relationship between temperature change of cell center and time under various laser spot radius of input laser power 35W
Figure 7. Relationship between radial temperature and radial length at 20s under various laser spot radius of input laser power 35W
Figure 8. a—relationship between photoelectric conversion efficiency and temperature with and without antireflection coating b—relationship between temperature change of cell center and time with and without antireflection coating
Table 1. Parameters of photoelectric conversion model
parameter value the Boltzmann constant kB/(J·K－1) 1.381×10－23 unit charge q/C 1.6×10－19 diode ideal factory A 2 intrinsic carrier concentration ni/cm-3 9.15×1019 (T/300)1.5×exp[－15.2/(T/300)] internal quantum efficiency at T0 Qe(T0) 0.95 internal quantum temperature coefficient kt 8×10－4 reflectivity R 0.1 laser wavelength λ/nm 1070 electron mobility μn/(cm2·V-1·s-1) 4000×(T/300)－2.5 hole mobility μp/(cm2·V-1·s-1) 2090×(T/300)－2.33 electron diffusion length Ln/μm 1.5 hole diffusion length Lp/μm 3 acceptor doping concentration Na/cm-3 1×1017 donor doping concentration Nd/cm-3 1×1018 
下载: 导出CSV
Table 2. Thermal parameters of Ge
parameter value density ρ /(kg·m-3) 5323.4 thermal conductivity κ /(W·cm-1·K-1) 0.6×(T /300)－1 specific heat capacity c /(J·kg-1·K-1) 303+6.13×10－2T energy gap Eg/eV 0.803－3.9×10－4T coefficient of heat transfer h /(W·m-2·K) 10 the Stefan constant σ /(W·m-2·K-4) 5.67×10－8 thermal radiation rate ε 0.1 laser radius a0/cm 1.5 cell radius b /cm 1.5 absorption coefficient α(T)/cm-1 1.4×104exp[2.81×(1.16+0.67－Eg－1.17)]
下载: 导出CSV
-
[1] XIANG X B, DU W H, CHANG X L, et al. The study on high effi-cient GaAs/Ge solar cells[J]. Solar Energy Materials & Solar Cells, 2001, 68(1):97-103. [2] TYAGI R, SINGH M, THIRUMAVALAVAN M, et al. The influence of As and Ga prelayers on the metal-organic chemical vapor deposition of GaAs/Ge[J]. Journal of Electronic Materials, 2002, 31(3):234-237. doi: 10.1007/s11664-002-0212-6 [3] GARG A, KAPOOR A, TRIPATH K N. Laser-induced damaged studies in GaAs[J]. Optics & Laser Technology, 2003, 35(1):21-24. [4] XUE Q, WU W H, YE Y X, et al. Property degradation of GaAs/Ge solar cells after femtosecond laser irradiation[J]. Laser & Optoelectronics Progress, 2015, 52(4):041405(in Chinese). [5] ZHU R Zh, WANG R, JIANG T, et al. Research of laser irradiation effect on monocrystalline silicon solar cells and single junction GaAs solar cells[J].Journal of Infrared and Millimeter Waves, 2015, 34(4):479-485(in Chinese). [6] SHANGHAI INSTITUTE OF SPACE POWER-SOURCES. Physical power technology[M].Beijing:Science Press, 2015:64-65(in Chinese). [7] STEINSIEK F, WEBER K H, FOTH W P, et al. Wireless power transmission experiment as an early contribution to planetary exploration missions[C]//International Astronautical Congress of the International Astronautical Federation. Bremen, Germany: International Academy of Astronautics, and International Institute of Space Law, 2003: 169-176. [8] BLACKWELL T. Recent demonstration of laser power beaming at DFRC and MSFC[C]//AIP Conference Proceeding Beamed Energy Propulsion. New York, USA: American Institute of Physics, 2005: 73-85. [9] KAWASHIMA N, TAKEDA K, TABE K. Application of the laser energy transmission technology to drive a small airplane[J]. Chinese Optics Letters, 2007, 5(s1):109-110. [10] QIU D D, JIN H S, SUN Y J. Damage effects research of solar cells under the irradiation of 1064nm CW laser[J]. Laser Journal, 2013, 34(2):23-24(in Chinese). [11] YANG H, LU J, ZHOU D Y, et al. Experimental study of 1070nm continuous wave fiber laser irradiation effect on three-junction GaAs solar cell[J]. Laser Technology, 2017, 41(3):318-321(in Chinese). [12] SHANGHAI INSTITUTE OF SPACE POWER-SOURCES. Physical power technology[M].Beijing:Science Press, 2015:45-47(in Chinese). [13] SHI J Q, OU H Y, MA Z Y, et al. A study of saturated current density of solar cells with pn junction[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2001, 29(4):24-26(in Chinese). [14] LANDIS G A. Photovoltaic receivers for laser beamed power in space[J]. Journal of Propulsion & Power, 1993, 9(1):1494-1502. [15] LI B B, LI X J. Numerical simulation of photovoltaic cell temperature field of laser power beaming[J]. Laser Technology, 2017, 41(4):537-537(in Chinese). [16] MEYER J R, KRUER M R, BARTOLI F J. Optical heating in semiconductors:laser damage in Ge, Si, InSb, and GaAs[J]. Journal of Applied Physics, 1980, 51(10):5513-5522. doi: 10.1063/1.327469 -
点击查看大图
计量
- 文章访问数: 10174
- HTML全文浏览量: 7747
- PDF下载量: 233
- 被引次数: 0
