激光熔覆过程中，相同的工艺参量下，不同扫描路径可以影响熔覆质量^[1]。国内外诸多学者针对扫描路径的生成算法进行了大量研究。SON等人^[2]提出了一种复杂模型的多重扫描方法，并成功研制出复杂零件表面扫描路径生成系统。BIAN等人^[3-4]提出了分组平行扫描路径的生成方法以及基于温度分区的扫描路径生成方法，解决了激光熔覆成形中出现的“过熔覆”、“欠熔覆”问题，较好地改善了熔覆层质量。DENG等人^[5]基于激光选区熔化提出了一种分区扫描方法，改善了成形零件残余应力的分布状态，提高了成形零件的力学性能，对于激光熔覆的扫描路径选择具有指导意义。在各种扫描路径生成方法中，由于平行扫描路径生成简单，而常被采用^[3]。然而实验中发现，若采用常用的同侧平行扫描路径，成形零件边界极易产生过烧和塌陷等缺陷。目前通常采用附加材料、添加等待时间或改变边界熔覆工艺参量来避免上述缺陷^[6]，但是上述方法会造成材料浪费、加工效率变低或工艺参量不合理。如果从扫描路径出发，研究扫描路径对温度场的影响规律以及影响程度，研究基体不同位置的散热规律，并选择能够避免边界热量过度累积的平行扫描路径，就可以在保证材料利用率、加工效率和工艺参量合理的同时更好地解决边界过烧和塌陷问题。

本文中从热传导的角度，分析了基体位置影响散热的规律，利用数值计算“生死单元”的方法研究了扫描路径对温度场的影响，发现不同扫描路径下的边界熔池温度相差很大。对反向熔覆和同侧熔覆的过烧和塌陷区域进行预测并实验验证，得出同向熔覆和异侧熔覆能够避免边界热量过度累积, 保证边界熔覆层质量，相比其它方法具有优越性。

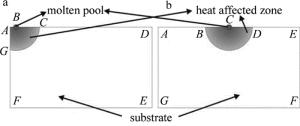
不同扫描路径下热累积、传导、辐射条件不同，温度场分布不同，熔覆层质量也不同，数值计算是一种计算激光熔覆温度场的重要方法^[7]。激光熔覆过程可以概括为激光由激光器发射，通过光缆传输至激光头并照射在基体表面，基体表面吸收激光能量迅速升温，形成熔池，金属粉末由送粉器通过送粉管道喷射到基体表面，落入熔池区域的金属粉末迅速熔化，并成为熔池部分。随着激光和基体的相对运动，离开激光束照射的熔池迅速冷却、凝固，形成熔覆层，如图 1所示。

Figure 1.  Laser cladding

本文中使用的基体与粉末材料均为316L不锈钢，其材料参量根据文献^[8-9]查得。采用ANSYS软件对多道激光熔覆温度场进行有限元数值计算。在数值计算前，通过单道单层激光熔覆实验，选择激光功率、扫描速率、送粉量等工艺参量，最终确定激光功率为1000W、扫描速率为5mm/s、送粉量为9.15g/min。通过测量单道单层熔覆层形貌，计算理论上的扫描间距^[10-11]为:

式中，C为扫描间距，S为熔覆层截面面积，H为熔覆高度。结合试错法最终确定扫描间距为1.5mm，在此工艺参量下形成的熔覆层如图 2所示。熔覆层厚度均匀，质量较好。

Figure 2.  Multitrack cladding layer

激光熔覆过程的热传导遵循傅里叶定律，可表示为:

式中, q为导热速率，λ为导热系数，s为导热面积，T为温度，n为传热面法线方向。进一步考虑基体温度和热传导的关系可以得到导热控制方程，表示为^[12]:

式中, c_p和ρ分别为316L不锈钢的比热容和密度，t为时间。假设激光能量服从均匀分布，熔覆过程中的热源模型为表面热源，热源模型可表示为:

式中, P_r′为理论激光功率密度，P为激光输出功率，R为光斑半径。由于激光束在穿过粉末流时，粉末对于激光有遮挡和散射的效果，考虑粉末的遮挡和散射效果后，实际激光功率密度可表示为^[13]:

式中, α为材料衰减因子，其值和材料本身有关; v为粉末颗粒的质量流动速率; R_p为粉末颗粒的平均半径; ρ_p为粉末密度; v_z为粉末颗粒在激光束方向的运动速率; Δz为激光头到基板间的垂直距离; η为激光吸收系数。粉末在下落过程中温度会不断升高，将(5)式带入粉末温升的数学模型^[14]可得:

式中，T_p为粉末颗粒的温度，Nu为努塞尔数，h_p和D_p分别为粉末的传热系数和平均直径。散热边界条件为第2类边界条件，遵循牛顿冷却公式，可表示为:

式中, q₁为热流密度，h为对流换热系数，T₀为外界温度。

由于激光熔覆过程涉及因素众多，为了简化熔覆过程温度场的求解，故做以下基本假设：(1)激光能量服从均匀分布；(2)金属粉末进入熔池后立即熔化并成为熔池一部分，不考虑熔池内部金属的流动，不考虑熔池自由表面的形成过程；(3)金属材料为各向同性，金属密度不随温度变化而变化，熔化潜热以焓的形式进行处理^[15]，不考虑金属材料的蒸发现象。

采用有限元计算软件ANSYS的APDL编程语言对激光熔覆过程进行建模。由于激光熔覆过程涉及粉末的添加，所以采用ANSYS“生死单元法”实现质量添加过程。激光扫描路径的差异体现在单元“重生”顺序的不同和激光光斑移动路径的不同。所建立的模型如图 3所示。模型尺寸为40mm×30mm×8mm，其中基体尺寸为40mm×30mm×7mm，模型上表面为熔覆层，熔覆层高度根据实验获得为1mm，熔覆层的长度和宽度即为基体的长度和宽度，将熔覆起点设置为原点，长边为激光连续扫描方向，短边为熔覆层搭接方向。为了尽可能地提高计算速度，温度变化剧烈区域的网格比较密集，而温度变化缓慢区域的网格比较稀疏，最终用ANSYS的SOLID70单元对模型进行网格划分。

Figure 3.  Schematic model and the meshed geometry

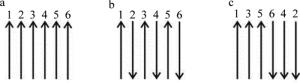
选择3种具有代表性的平行扫描路径进行温度场计算，研究扫描路径对于热量累积和温度场分布的影响规律。各种扫描路径及其命名方式如图 4所示。其中竖直线为单道扫描路径，数字为多道熔覆时熔覆层搭接顺序。

Figure 4.  Three kinds of parallel scanning paths

本文中计算温度场的时间步为0.2s，单道熔覆时间为8s，即40个时间步，共有19道，熔覆过程假设没有停歇，整体熔覆时间为152s，共760个时间步。熔覆过程中，熔覆层单元按照图 4所示的既定扫描路径依次“重生”，“重生”单元的初始温度通过(6)式计算得到。激光作为表面热源处理，在每一时间步开始时添加到对应熔覆层单元的上表面，在每一时间步计算结束后删除，激光热源模型通过(5)式计算得到。基体和熔覆层表面除激光照射以外的区域均添加散热边界条件，在每一时间步被“重生”单元格覆盖的边界，对其散热边界条件进行删除。

图 5为不同扫描路径下最后时间步的温度场分布。观察发现，在热量累积时间相同的情况下，不同扫描路径最后时间步的温度场分布不同，异侧熔覆熔池温度低于同侧熔覆熔池温度约500℃，而异侧熔覆基体最低温度比同侧熔覆基体最低温度高100℃左右，这说明相比同侧熔覆，异侧熔覆的熔池热量更多地传导到基体中，基体受热更加均匀。

Figure 5.  Temperature field distribution in the final time step of different scanning paths

比较同向和反向熔覆中同一道熔池最高温度的变化情况。熔覆道数为19，选择第10道熔覆层作为研究对象，分别做出该熔覆层上的熔池最高温度随时间的变化曲线，并将该道熔覆的起始时间记为0s，结果如图 6所示。观察图 6发现, 两者两端熔池最高温度差异较大。同侧同向熔覆时，熔池最高温度的初始值很低，在0.6s内迅速上升，在0.6s后熔池最高温度逐渐稳定在2100℃左右，并一直持续到最后。而反向熔覆初期熔池最高温度也呈现急速上升趋势，其初始值约为2100℃，最高值约为2500℃，然后熔池最高温度随时间逐渐降低，大约3s左右熔池最高温度趋于稳定。

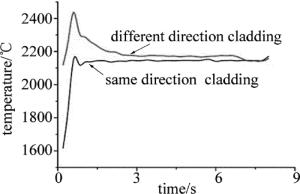
Figure 6.  Relatoinship between the maximum temperature of the molten pool in the tenth cladding process and time

多道熔覆时，取每道熔覆中间时刻的熔池最高温度代表该道熔覆时熔池平均最高温度，做出同侧和异侧熔覆每道熔池平均最高温度随熔覆道数的变化曲线，如图 7所示。观察图可发现：同侧熔覆熔池平均最高温度在边界处剧烈增加。异侧熔覆的熔池平均最高温度较为稳定，并且在边界层上低于同侧熔覆熔池平均最高温度约500℃。

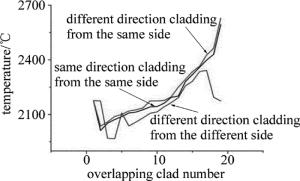
Figure 7.  Relatoinship between the average maximum temperature of the molten pool and the cladding number

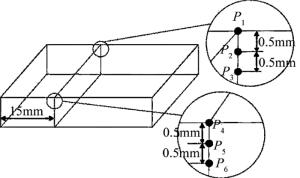
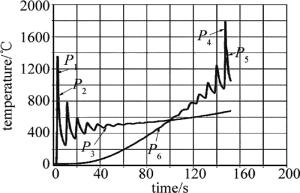
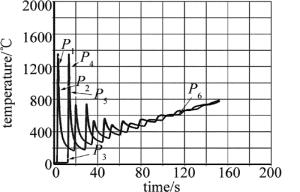
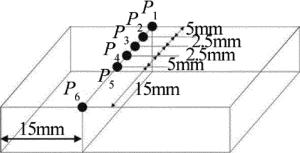
取边界上的6个点，位置如图 8所示。观察它们的温度随时间的变化情况，如图 9和图 10所示。观察两组曲线可以发现，同侧熔覆时，P₄, P₅, P₆这3点的最高温度分别约为1900℃, 1600℃, 1400℃，P₄, P₅两点最高温度超过316L熔点，316L熔化并发生塌陷。异侧熔覆时，P₄, P₅, P₆这3点最高温度分别约为1400℃, 1125℃, 800℃。

Figure 8.  Schematic diagram of test point position

Figure 9.  Relationship between the temperature of different test points in the same side cladding and time

Figure 10.  Relationship between the temperature of different test points in different side cladding and the time

本文中采用的实验装置为半导体激光熔覆系统，包括Laserline半导体激光器、KUKA六轴机器人、Precitec的YC52同轴激光熔覆头以及载气式同轴送粉器，如图 11所示。实验中使用的基体和粉末材料均为316L不锈钢，粉末粒度为45μm~180μm，粉末质量分数为：0.00006C, 0.026Mo, 0.128Ni, 0.015Mn, 0.17Cr, 0.007Si，其余为Fe。载粉气体和保护气体皆为高纯度氩气。

Figure 11.  Laser cladding system

在实验前用粗砂纸将基体进行打磨，去除基体表面的油污及氧化层。保证总体熔覆时间相同的情况下分别按照图 4中的3种扫描路径进行激光熔覆，得到3种熔覆结果, 如图 12所示。观察图 12可知，同侧同向熔覆和同侧反向熔覆的熔覆层形貌基本相同，但是在前表面，同侧反向熔覆基体出现一系列半圆形的过烧区域，这主要是由于在反向熔覆过程中，边缘部分的熔池温度超过激光熔覆的正常温度，因此形成了深色的过烧区域，其形状与熔池形状大致相同。而同侧同向熔覆基体前表面温度大大低于激光熔覆熔池所允许的正常温度，所以没有形成深色的过烧区。

Figure 12.  Surface profile under different scannning paths

如图 13所示，观察不同扫描路径下边界处的熔覆质量。虽然异侧熔覆边界处也产生了过烧区域，但是该区域厚度极小，在边界处没有发现熔覆层的过度氧化。同侧熔覆无论是同向还是反向，边界熔覆层呈黑色，均有不同程度的氧化。侧面观察发现，同侧熔覆边界处出现了过烧和塌陷，而且在边角处过烧情况更加严重，异侧熔覆边界质量很好，没有出现过烧及塌陷的现象。

Figure 13.  Boundary cladding quality under different scanning paths

激光照射为一个热量剧烈累积的过程，在激光熔覆过程中，热量随着激光光斑的移动在基体的不同位置迅速累积。熔覆初期，激光逐渐照射在基体表面，热量迅速累积，因此每道熔覆初期，熔池温度迅速增加。随着激光和基体的相对运动，温度较低的基体不断进入熔池区域，熔池传热量、导热量、辐射热量、热力学能增量与吸收热量相平衡，熔池温度逐渐稳定。多道熔覆时，热量在熔池附近的基体上不断累积，导致下一道熔覆时基体初始温度升高，熔池平均最高温度随熔覆道数的增加而增加。

在激光功率为1000W、扫描速率为5mm/s、送粉量为9.15g/min、扫描间距为1.5mm、基体尺寸为40mm×30mm×7mm时，由数值计算和实验结果可得，同向熔覆的熔池温度比反向熔覆更快达到稳定，反向熔覆初期熔池最高温度比同侧熔覆高约300℃，可能会引起过烧、氧化等问题，因此可以预测相邻两道熔覆层反向熔覆时，每道起始端和终端容易产生过烧和氧化等缺陷，将反向熔覆改为同向熔覆就可以很好地解决这一问题。相同边界位置处同侧熔覆熔池温度比异侧熔覆熔池温度高500℃以上，相同熔覆时间下同侧熔覆的熔池温度高于异侧熔覆熔池温度，最后时刻的温差约为500℃。同侧熔覆的边界易产生过烧和塌陷等缺陷。对于基体温度场，同侧熔覆基体最高温度和最低温度相差约为2000℃，异侧熔覆基体最高温度和最低温度相差约为1400℃，异侧熔覆基体最低温度比同侧熔覆基体最低温度高约100℃，这说明异侧熔覆时，熔池热量更多地传导至基体中，能够使熔池温度降低、基体温度分布更加均匀。

基体不同位置的散热方式和散热面积不同。在基体内部，温度传导遵循傅里叶定律，而在边界处温度的传导则遵循牛顿冷却公式，比较基体内部和边界处散热情况，为简化计算仅考虑其2维截面上的散热情况，如图 14所示。

Figure 14.  Schematic diagram of heat dissipation in the different regions of substrate

考虑以熔池为圆心，半径为R₁区域的温度传导情况，对于边界区域来说，散热可表示为:

式中，εv为辐射率，σ₀为热辐射常数。内部区域散热可表示为:

式中，Q₁和Q₂为单位时间散热量，L_GA，L_AC和L_BD表示直线段，S_CG和S_DB表示曲线段。激光直径为3mm，设图 14a中AB=1.5mm。如果考虑一种最简单情况：熔池为1个点，温度梯度值在圆弧线上处处相等，按照圆弧区域内部平均温度梯度计算，温度在边界上均匀变化，比较散热量的区别。假设熔池温度为2500℃，R₁=5mm，圆弧线上温度为1000℃，其余材料参量均参照参考文献[8]和参考文献[9]，计算可得基体内部散热速率约为边界处的1.65倍。

综上所述，对于激光熔覆而言边界为基体的“薄弱”区域，同向熔覆保证了单道熔池温度的稳定，异侧熔覆先熔覆基体“薄弱”的边界区域，再熔覆基体内部，一方面保证了边界质量，另一方面提高了熔覆后期熔池散热能力，使整体温度场分布更加均匀，能够避免边界过烧、塌陷，与添加等待时间、改变工艺参量、使用附加材料等方法相比具有优越性。

熔池冷却速度和温度梯度影响熔覆层微观组织，将同侧熔覆和异侧熔覆试样沿图 15所示截面进行线切割、研磨、抛光，抛光后用饱和草酸溶液在5V直流电压下进行电解腐蚀，利用金相显微镜观察同侧熔覆P₁，P₅，P₆点，异侧熔覆P₁，P₂，P₃，P₄，P₅，P₆点的显微组织，如图 16、图 17所示。同侧熔覆过程中，热量的不断累积和边界不断减小的散热速率使得熔池的冷却速率随着熔覆时间的增加而减小，熔覆层晶粒尺寸及生长方式均在不断变化，熔覆层各部分微观组织相差较大。异侧熔覆时，边界处P₆点的晶粒细化程度明显优于同侧熔覆，基体内部晶粒尺寸及生长方式相差不大，基体内部热量的不断累积和散热速率达到了较好的平衡关系。因此，采用异侧扫描路径熔覆的零件表面质量好、内部性能一致，具有更加优良的性能。

Figure 15.  Schematic diagram of test points position

Figure 16.  Microstructure of cladding layer at different locations in same side cladding

Figure 17.  Microstructure of cladding layer at different locations in different side cladding

(1) 单道熔覆时，熔池最高温度在波动后趋于稳定；多道熔覆时，熔池最高温度基本上随熔覆道数的增加而增加。

(2) 边界处基体散热条件差，同向熔覆和异侧熔覆能避免边界熔覆前的热量累积，在保证高加工效率、材料利用率以及合理工艺参量的同时大幅度降低了边界熔覆温度，保证边界熔覆质量。在激光功率为1000W、扫描速率为5mm/s、送粉量为9.15g/min、扫描间距为1.5mm、基体尺寸为40mm×30mm×8mm条件下，同向熔覆边界处熔池最高温度比反向熔覆低约300℃，异侧熔覆边界处熔池最高温度比同侧熔覆低约500℃。反向熔覆和同侧熔覆边界更易产生过烧、塌陷等缺陷。

(3) 同侧熔覆时，热量的不断累积和边界散热速率的不断减小使得熔池的冷却速率随着熔覆时间的增加而减小，熔覆层组织分布不均。异侧熔覆可以使热量累积与散热速率间的关系更加平衡，整体温度场分布更为均匀，熔覆层边界晶粒细密、内部组织分布均匀，具有更加优良的性能。