-
在光通信系统中,随着通信速率的增加,偏振效应产生的损害对通信系统性能的影响也会越来越显著。两个光束在相干光传输系统中进行叠加就需要严格控制光束的偏振状态[1-4];而在密集波分复用光通信中存在极化模式色散的问题,偏振控制器可以补偿极化模式色散, 从而提高通信链路的质量[5-9]。因此,偏振控制是光通信链路中必不可少的一个环节。同时偏振控制在光纤光栅特性分析中也有重要应用[10]。
偏振控制器可以通过改变波片结构的光轴方向或者相位延时量改变入射光束偏振方向,从而达到控制输出光束偏振态的目的。在参考文献[11]中,用双折射晶体实现波片结构,通过改变晶体的折射率,使输出光束偏振态发生改变。波片结构的功能也可以用移相器代替实现[12]。当然也可以用全光的方法或者其它方法实现不同的偏振控制[13-14]。总的来说,偏振控制器可以通过两种方式对输入光束进行偏振控制。对于相位固定-方向可调的偏振控制器,输入光经过该偏振控制器的相移一定,通过改变偏振控制器件的光轴方向实现输出偏振态的改变[11, 15-17]。λ/4波片-λ/2波片-λ/4波片(quarter-half-quarter wave-plate, QHQ)型偏振控制器就是一种典型的相位固定-方向可调的偏振控制器[18]。在QHQ型偏振控制器中,改变输入光偏振态的主要方法是改变3个波片光轴的相对角度。通过改变光轴角度,第2个λ/2波片将第1个λ/4波片输出的线偏振光旋转到目标偏振方向,最后再利用第3个λ/4波片输出目标偏振态。而另一种常用的偏振控制器则是方向固定-相位可调型的偏振控制器。这类偏振控制器一般由光轴互成45°的多个波片组成。波片则由具有电光效应的材料制成,如液晶、电光陶瓷等。在偏振控制的过程中,该类偏振控制器内各波片的光轴方向是固定的,通过改变加载在波片上的电压改变由各波片引入的相移,从而达到偏振控制的目的[18-19]。在本文中,作者采用方向固定-相位可调型的偏振控制器,通过设计一种新型的偏振控制算法,对输入光的偏振态进行快速控制。
而在偏振控制的过程中,由两个波片级联构成的偏振控制器存在偏振“盲区”问题[11-12, 20]。如果输入光束为一些特殊的偏振态,输出光束不能为某些偏振态,则存在“盲区”。“盲区”问题严重影响了偏振控制器的性能。在作者所在课题组之前的工作[21-22]中,设计了一种基于模拟退火算法的偏振控制器。用全局收敛性较好的模拟退火算法代替在多驻点情况下全局收敛不敏感的梯度法进行偏振控制,保证了偏振控制过程的稳定性。但是在该偏振控制器中,实际使用的波片只有两片,另外两片波片是用来保证复位过程相位变化的稳定性的,并没有解决偏振“盲区”问题,而且响应速度较慢,在100ms量级上。在本文中,通过三波片级联的方式,利用增加的首级波片,将输入光束的偏振态变化到中间偏振态,使得原处于输入光束偏振态对应“盲区”的输出光束偏振态处于中间偏振态的可控区域内。同时,在从中间偏振态变化到目标偏振态的过程中,将粗调和细调相结合,在粗调中采用精确度不高的分布逼近算法,降低控制算法整体的复杂度,提高控制速度,而仅在细调中采用精确度较高的比例-微分(proportional-differential, PD)算法,从而在保证提高偏振控制速度的同时确保输出偏振态的精度。同时整个偏振控制系统采用了反馈结构,能够较好地消除由于旋转主轴偏移以及铁电陶瓷自身的回滞特性所引起的系统的不稳定。
-
用邦加球来表示光束的偏振态。邦加球球面上的点都唯一对应了一种完全偏振态,而该点的坐标值对应一组归一化斯托克斯参量。
用A0, A1, A2, A3表示斯托克斯参量,各个斯托克斯参量可定义为[23]:
$ \left\{ \begin{array}{l} {A_0} = |{E_x}{|^2} + |{E_y}{|^2}\\ {A_1} = |{E_x}{|^2} - |{E_y}{|^2}\\ {A_2} = 2{E_x}{E_y}{\rm{cos}}\delta \\ {A_3} = 2{E_x}{E_y}{\rm{sin}}\delta \end{array} \right. $
(1) 式中, Ex为x方向的电场,Ey为y方向的电场,δ表示Ex和Ey之间的相位差; A0表示总光强,A1表示x,y方向上的光强差,A2表示-45°和45°方向上的光强差,A3表示右旋偏振与左旋偏振的光强差; 归一化斯托克斯参量S1, S2, S3则分别是A1, A2, A3对A0总光强的归一。归一化斯托克斯参量组成的矢量可以表示为邦加球上的点。因此,可以从邦加球上直观地看出光的偏振态。邦加球赤道面S1OS2上的点表示线偏振光,赤道面与S1轴正向的交点表示水平线偏振光,而对称点则表示垂直线偏振光;越靠近两极,表示光偏振的椭圆率越小,S3轴正向与邦加球球表面的交点表示右旋偏振光,其对称点表示左旋偏振量光。
而偏振波片对输入光的偏振变化情况通常用穆勒矩阵表示。在本文中用到的光轴方向角为0°,45°的旋转波片的穆勒矩阵可以表示为:
$ {\mathit{\boldsymbol{M}}_{0^\circ }}({\varphi _1}) = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&1&0&0\\ 0&0&{{\rm{cos}}{\varphi _1}}&{{\rm{sin}}{\varphi _1}}\\ 0&0&{ - {\rm{sin}}{\varphi _1}}&{{\rm{cos}}{\varphi _1}} \end{array}} \right] $
(2) $ {\mathit{\boldsymbol{M}}_{45^\circ }}({\varphi _2}) = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&{{\rm{cos}}{\varphi _2}}&0&{ - {\rm{sin}}{\varphi _2}}\\ 0&0&1&0\\ 0&{{\rm{sin}}{\varphi _2}}&0&{{\rm{cos}}{\varphi _2}} \end{array}} \right] $
(3) 其中的自变量则为各波片引入的相移。因此光轴方向与水平方向分别成45°,0°和45°的旋转波片组成的系统的输出偏振态可以分别表示为:
$ {\mathit{\boldsymbol{S}}_{{\rm{out}}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&{{\rm{cos}}{\varphi _1}{\rm{cos}}{\varphi _3} - {\rm{sin}}{\varphi _1}{\rm{cos}}{\varphi _2}{\rm{sin}}{\varphi _3}}&{{\rm{sin}}{\varphi _2}{\rm{sin}}{\varphi _3}}&{ - {\rm{sin}}{\varphi _1}{\rm{cos}}{\varphi _3} - {\rm{cos}}{\varphi _1}{\rm{cos}}{\varphi _2}sin{\varphi _3}}\\ 0&{{\rm{sin}}{\varphi _1}{\rm{sin}}{\varphi _2}}&{{\rm{cos}}{\varphi _2}}&{{\rm{cos}}{\varphi _1}{\rm{sin}}{\varphi _2}}\\ 0&{{\rm{cos}}{\varphi _1}{\rm{sin}}{\varphi _3} + {\rm{sin}}{\varphi _1}{\rm{cos}}{\varphi _2}{\rm{cos}}{\varphi _3}}&{ - {\rm{sin}}{\varphi _2}{\rm{cos}}{\varphi _3}}&{ - {\rm{sin}}{\varphi _3}{\rm{sin}}{\varphi _1} + {\rm{cos}}{\varphi _1}{\rm{cos}}{\varphi _2}{\rm{cos}}{\varphi _3}} \end{array}} \right]{\mathit{\boldsymbol{S}}_{{\rm{in}}}} $
(4) 式中, φ1, φ2, φ3分别为在第一波片、第二波片、第三波片上引入的相移。
-
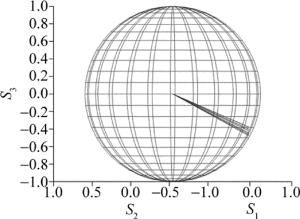
本文中所用的偏振控制器由4片锆钛酸铅镧电光陶瓷PLZT波片和一个高压驱动模块组成。若仅使用其中的两片晶体波片进行偏振控制,即当加在第二波片上的电压改变的同时,对第三波片所加的电压进行遍历,输出光的偏振态如图 1所示。从图 1中可以看出,双波片偏振控系统存在控制盲区,不能输出邦加球两极附近区域所对应的偏振态。在双波片系统中,盲区在邦加球中的位置满足不等式:
$ |{S_{{\rm{2, out}}}}| > \sqrt {{S_{{\rm{1, in}}}}^2 + {S_{{\rm{3, in}}}}^2} $
(5) 式中, S2, out是输出光束在S2轴上的分量值,S1, in和S3, in则分别是输入光束在S1,S3轴上的分量值。因此,图 1中也给出了对于特定输入偏振态的输出光偏振态的可控区域范围。
从盲区范围不等式可以看出,只要输入光的偏振态处于S2=0平面内,则可实现双波片系统的全偏振态控制。因而在本文中,解决盲区问题的方法是在双波片系统之前增加一个波片,利用新增的波片将输入偏振态变换到处于S2=0平面内的中间偏振态,然后再将中间偏振态通过双波片系统控制到任意偏振态输出。
-
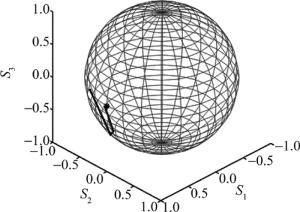
在三波片偏振控制系统中,在理想情况下,当第二波片的控制电压改变时,第三波片的旋转主轴应该维持不变。但实际上,第二波片上电压的改变也会导致第三波片的旋转主轴方向发生偏转。如图 2所示,当第二波片上的控制电压以0.1V步长变化时,第三波片的主轴方向发生的最大偏转角度约为5°。主轴方向偏转现象会使误差累加,是在偏振控制系统中存在的不稳定因素。
而在该偏振控制系统中,制成波片的材料PLZT是一种铁电陶瓷。铁电陶瓷自身具有电滞回特性,会导致偏振控制器在高速连续控制中会产生误差。由于PLZT的电滞回特性,在波片上先增加一定电压再减少相同电压,最后的输出偏振态和初始偏振态并不在邦加球上的同一点上。这一点限制了整个偏振控制系统的精度,并容易造成一般的控制算法在目标点附近产生振荡,也是在偏振控制系统的一个不稳定因素。
由于偏振系统存在上述可能引入误差的不稳定因素,因此,本文中设计的偏振控制系统是一个带反馈的闭环系统,在偏振控制的过程中通过不断地将一部分输出信号反馈到控制电压产生部分,实时调整输入到波片上的控制电压,保证系统的稳定性。而对于带反馈的偏振控制系统,为了实现对偏振态的实时控制,则需要设计一个快速偏振控制算法。
-
在双波片控制系统中,一般采用PD算法进行偏振控制。但是PD算法是一种精确度较高的算法,因此算法的复杂度较高,降低了算法的运行速度,不利于进行实时的偏振控制。因此本文中,在从中间偏振态变换到目标偏振态的过程中,将粗调和细调相结合,仅在细调过程中采用较复杂高精度的PD控制算法,在粗调的过程中则采用较简单精度不高的分布逼近算法。分步逼近算法虽然也要考虑控制范围的问题,但是没有PD算法那么严格,对波片线性度的要求也不高,只要所加电压在波片工作区域内即可,并且该算法的平均步长在4步左右,从而较大程度地降低了控制算法的复杂度,提高了算法的运算速度,进一步地保证了偏振控制的实时性。图 3则为本文中所设计算法的框图结构。
同时,该算法的初始化过程对整个系统的稳定性具有重要的作用。在初始化过程中,对波片的控制电压进行扫描遍历,将对应的控制参量存入表格备用。为了消除由于PLZT自身的电滞回特性引起的系统不稳定性,采用S型扫描,即将增加控制电压和减少控制电压的结果进行分别存储。表 1中给出了部分实际控制参量。
Table 1. Control parameter in the initial process
control voltage of the 1st wave-plate/V control voltage of the 2nd wave-plat/V control parameter 1.600 2.000 9.4933 1.600 2.250 11.8780 1.700 2.000 12.2870 1.700 2.250 11.6160 2.400 2.000 5.4672 2.400 2.250 9.7153 -
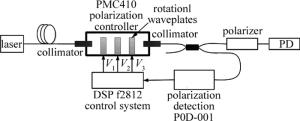
该偏振控制器由3片波片级联组成,3片波片的快轴互成45°,第一波片、第二波片、第三波片与水平方向分别成45°,0°和45°。系统的硬件结构如图 4所示。该系统具有一个反馈结构,从偏振控制器中出来的输出光束经过5/95光路分束器之后,一路作为输出光束输出,另一路则作为偏振控制算法的输入参量得到偏振现态点。通过偏振控制算法,得到所需要的控制电压,再将控制电压加到PLZT晶体波片上,从而将任意偏振态的输入光束控制到目标偏振态输出。
在如图 4所示的实验系统中,作者采用保偏光纤连接各个实验模块,从而保证系统的精度和稳定性。
-
基于本文中所提出的实时快速偏振控制算法,在上述硬件系统中对该偏振算法的性能进行测量。如果想要得到水平线偏振的输出光束,并将该系统输出的光束输入到POD-001水平偏振检测其中进行检测。实验结果如表 2所示。从结果中可以看出,对于任意输入偏振态,该系统输出光束的偏振态均被控制在目标偏振态(1, 0, 0)附近。采用不同的输入偏振态,在实验中的输入偏振态既有左旋偏振态(0.44206260,0.70274700,-0.55742900),也有右旋偏振态(0.78678050,-0.04899382,0.61528530),经过该快速偏振控制算法,得到合适的偏振电压之后,加载在相应的偏振波片上,得到的输出偏振态均在水平线偏振态附近。
Table 2. The control voltage of the polarization controller and the polarization state of the output beam
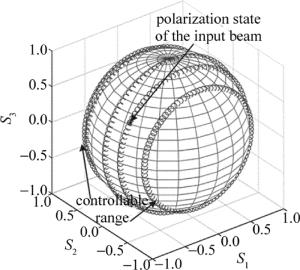
the input polarization state control voltage/V the output polarization state (-0.50249240, 0.86316150, -0.04953419) (2.225, 2.600, 2.250) (0.99913450, -0.03485601, -0.02269625) (0.78678050, -0.04899382, 0.61528530) (2.975, 1.800, 2.250) (0.99539230, 0.06506954, 0.07042807) (0.44206260, 0.70274700, -0.55742900) (2.475, 2.400, 2.250) (0.91107190, 0.03284634, -0.41093690) 表 3中给出了第三波片的主要振态(principle state of polarization, PSP)所对应的归一化斯托克斯参量在x, y, z方向上的分量值。其中PSPx表示x方向的归一化斯托克斯参量,PSPy表示y方向的归一化斯托克斯参量,而PSPz表示z方向的归一化斯托克斯参量。如表 3所示,在实际测量中,当第二波片的电压发生改变,第三波片的旋转主轴则发生偏转,影响了偏振控制系统的稳定性。因此引入了反馈结果,当输出偏振态发生漂移时,快速将输入偏振态控制到目标偏振态附近。如图 5所示,*处表示目标偏振态在邦加球上的位置,用线条将反馈系统调整过程中的输出偏振态在邦加球上的点相连, 则该线条表示当偏振态发生漂移之后,通过反馈系统恢复到目标偏振态附近的整个过程。
Table 3. Deflection of the rotational axis of the 3th wave-plate
the control voltage of the 2nd wave-plate/V PSPx PSPy PSPz 1.600 0.6517 -0.6318 -0.4196 1.800 0.6011 -0.6624 -0.4472 2.000 0.7050 -0.6003 -0.3777 2.200 0.5784 -0.6724 -0.4619 2.400 0.6709 -0.6230 -0.4022 2.500 0.5685 -0.6726 -0.4737 -
基于波士顿应用科技公司的偏振控制器PCM410和通用光电在线高速检偏器POD-001搭建的偏振实时控制系统,可在误差允许的范围内实现实时偏振控制。提出了通过前波片模糊控制,主要应用后两级双波片系统完成精确控制的控制算法。目前响应速度为10ms量级。进一步工作可集中在提高偏振控制器线性度、减小测量及控制误差和提升模糊控制准确性方面。
实时快速偏振控制算法设计
Design of real-time fast polarization control algorithm
-
摘要: 为了有效地解决方向固定-相位可调型偏振控制器偏振盲区问题,同时实现对该偏振控制器输出光束偏振态的快速实时控制,采用三波片级联的偏振控制器,设计了新的偏振控制算法,通过分步逼近算法粗调以及比例-微分算法细调相结合的方法,降低了偏振控制算法的复杂度,提高了偏振控制的速度。结果表明,该偏振算法有效地控制了输出光束的偏振态,使其始终在目标偏振态附近,且该偏振控制器的响应速度在10ms量级。在增加反馈系统的基础上,该偏振控制器达到了实时快速稳定地控制输出偏振态的目的。Abstract: In order to solve the "blind area" problem and control the polarization state of the output optical beam of the polarization controller in real-time, a new polarization control algorithm was proposed by using three cascading waveplates. The complexity of the algorithm was reduced and the speed of the polarization control was improved by combining the coarse control (the step-by-step approach algorithm) and the fine control (the proportional-differential algorithm). Through theoretical analysis and experimental test, the results show that the algorithm does well so that the polarization state of the device's output optical beam is always near the objective state. And the response time of the polarization controller is about 10ms. The polarization controller proposed in the paper has achieved the aim of real-time controlling the output polarization state fast and steadily by adding the feedback structure into the polarization control system.
-
Table 1. Control parameter in the initial process
control voltage of the 1st wave-plate/V control voltage of the 2nd wave-plat/V control parameter 1.600 2.000 9.4933 1.600 2.250 11.8780 1.700 2.000 12.2870 1.700 2.250 11.6160 2.400 2.000 5.4672 2.400 2.250 9.7153 Table 2. The control voltage of the polarization controller and the polarization state of the output beam
the input polarization state control voltage/V the output polarization state (-0.50249240, 0.86316150, -0.04953419) (2.225, 2.600, 2.250) (0.99913450, -0.03485601, -0.02269625) (0.78678050, -0.04899382, 0.61528530) (2.975, 1.800, 2.250) (0.99539230, 0.06506954, 0.07042807) (0.44206260, 0.70274700, -0.55742900) (2.475, 2.400, 2.250) (0.91107190, 0.03284634, -0.41093690) Table 3. Deflection of the rotational axis of the 3th wave-plate
the control voltage of the 2nd wave-plate/V PSPx PSPy PSPz 1.600 0.6517 -0.6318 -0.4196 1.800 0.6011 -0.6624 -0.4472 2.000 0.7050 -0.6003 -0.3777 2.200 0.5784 -0.6724 -0.4619 2.400 0.6709 -0.6230 -0.4022 2.500 0.5685 -0.6726 -0.4737 -
[1] NOE R, HEIDRICH H, HOFFMAN D. Automatic endless polarization control with integrated-optical Ti:LiNbO3 polarization transformers[J]. Optics Letters, 1988, 13(6):527-529. doi: 10.1364/OL.13.000527 [2] ZHANG X G. Progress of polarization control technologies in high speed optical fiber communications[J]. Journal of Beijing University of Posts and Telecommunications, 2011, 34(1):1-10(in Chinese). [3] GONG Y D, CHEN Sh Q, JIAN Sh Sh. Polarization problem in coherent optical communication[J]. Optical Communication Technology, 1995, 19(2):21-29(in Chinese). [4] NOE R, KOCH B, MIRVODA V, et al. 38-krad/s 3.8-Grad broadband endless optical polarization tracking using LiNbO3 device[J]. IEEE Photonics Technology Letters, 2009, 21(17):1220-1222. doi: 10.1109/LPT.2009.2024549 [5] NOE R, SANDEL D, MIRVODA V. PMD in high-bit-rate transmission and means for its mitigation[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2004, 10(2):341-355. doi: 10.1109/JSTQE.2004.827842 [6] NOE R, SANDEL D, YOSHIDA-DIEROLF M, et al. Polarization mode dispersion compensation at 10, 20, and 40Gb/s with various optical equalizers[J]. Journal of Lightwave Technology, 1999, 17(9):1602-1616. doi: 10.1109/50.788566 [7] KHOSRAVANI R, HAVSTAD S A, SONG Y W, et al. Polarization-mode dispersion compensation in WDM systems[J]. IEEE Photonics Technology Letters, 2001, 13(12):1370-1372. doi: 10.1109/68.969911 [8] BOZINOVIC N, YUE Y, REN Y X, et al. Terabit-scale orbital angular momentum mode division multiplexing in fibers[J]. Science, 2013, 340(6140):1545-1548. doi: 10.1126/science.1237861 [9] ZHANG X G, YU L, ZHEND Y, et al. Two-stage adaptive PMD compensation in a 10Gbit/s optical communication system using particle swarm optimization algorithm[J]. Optical Communication, 2004, 231(1):233-242. [10] RAO M H, HE Zh J, YANG G L, et al. The advance of polarization control method to ultraviolet-written Bragg gratings[J]. Laser Technology, 2004, 28(1):61-64(in Chinese). [11] RONG W F, DUPONT L. A feedback algorithm for polarization control using two rotatable wave plates with variable birefringence[J]. Optics Communications, 2006, 259(2):603-611. doi: 10.1016/j.optcom.2005.09.032 [12] MADSEN C K, OSWALD P, CAPPUZZO M, et al. Reset-free integrated polarization controller using phase shifters[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2005, 11(2):431-438. doi: 10.1109/JSTQE.2005.846538 [13] YU Zh H, XIAO P P. Controllable laser polarizer based on twice attenuation total reflection structures[J]. Laser Technology, 2013, 37(1):82-84(in Chinese). [14] YUAN M, QIN Z J, YANG K. Research of polarization control based on bi-propagating dual-order Raman pump[J]. Laser Technology, 2016, 40(6):860-865(in Chinese). [15] LIAO Y N, ZHANG W, YIN Y F, et al. Research on and analysis of polarization controllers using rotatable retarders[J]. Study on Optical Communications, 2010, 157(1):51-54(in Chinese). [16] HIRABAYASHI K, AMANO C. Feed-forward continuous and complete polarization control with a PLZT rotatable-variable waveplate and inline polarimeter[J]. Journal of Lightwave Technology, 2003, 21(9):1920-1932. doi: 10.1109/JLT.2003.816891 [17] WANG J L, FANG Q, WANG Y Ch, et al. Two novel methods for polarization transformer using rotatable waveplates[J]. Acta Optica Sinica, 2005, 25(1):21-26(in Chinese). [18] ZHAO N, LI X Y, LIU J H. The development of polarization controller[J]. Journal of Xi'an University of Post and Telecommunications, 2008, 13(3):13-16(in Chinese). [19] ZHUANG Zh Zh, SUH S W, PATEL J S. Polarization controller using nematic liquid crystals[J]. Optics Letters, 1999, 24(10):694-696. doi: 10.1364/OL.24.000694 [20] WANG J L, LI J. Error analysis on two-waveplate polarization state transformers by geometry method[J]. Optik-International Journal for Light and Electron Optics, 2010, 121(8):711-714. doi: 10.1016/j.ijleo.2008.11.006 [21] LI W W, ZHANG X M, CHEN K Sh, et al. A study for phase shift characteristics of polarization controller based on simulated annealing algorithm[J]. Acta Optica Sinica, 2005, 25(4):449-453(in Chinease). [22] LI W W, ZHANG X M, CHEN K Sh, et al. Application of simulated annealing algorithm on endless polarization controller[J]. Acta Photonica Sinica, 2005, 34(6):820-824(in Chinese). [23] LIU Y. Research on polarization controller and its control algorithm[D]. Hangzhou: Zhejiang University, 2008: 31-41(in Chinese). -


 网站地图
网站地图

 下载:
下载: