Sensitization design of liquid dual parameter sensor based on fiber grating
-
摘要: 为了解决现有光纤布喇格光栅(FBG)传感器温度与压力灵敏度低的问题, 设计了一种基于FBG的薄壁圆筒式液体温度与压力传感器。选用具有耐腐蚀、弹性性能好以及热膨胀系数大的不锈钢304和铍青铜C17200分别对传感器进行封装, 采用有限元分析法对传感器进行压力和温度特性仿真分析, 研究了敏感元件材料及尺寸大小对灵敏度的影响, 并分析了反射波长随压力和温度的变化关系。结果表明, 使用铍青铜C17200封装的传感器压力和温度灵敏度更高, 在0MPa~12MPa、-5℃~40℃工作范围内压力灵敏度可达153.5pm/MPa、温度灵敏度可达31.7pm/℃, 相较于裸光栅分别提升了51.2倍和2.8倍。此研究结果可为液体的高灵敏度温压测量提供参考。Abstract: In order to solve the problem of low temperature and pressure sensitivity of the existing fiber Bragg grating (FBG) sensors, a thin-walled cylindrical liquid temperature and pressure sensor based on FBG was designed. Both the stainless steel 304 and beryllium bronze C17200 with corrosion resistance, good elasticity, and high coefficient of thermal expansion were used to package the sensor. The finite element analysis method was used to simulate the pressure and temperature characteristics of the sensor. The influence of the material and size of the sensitive element on the sensitivity was studied, and the relationship between the reflection wavelength and the pressure and temperature was analyzed. The results show that the sensor encapsulated with beryllium bronze C17200 has higher pressure and temperature sensitivity, which can respectively reach 153.5pm/MPa and 31.7pm/℃ in the operating range of 0MPa~12MPa and -5℃~40℃, which are increased by 51.2 times and 2.8 times respectively on the basis of the bare grating, respectively. It is expected to be applied to high sensitivity measurement of liquid temperature and pressure. The results can provide reference for high sensitivity temperature and pressure measurement of liquid.
-
引言
传统的液体温度与压力检测，以较高精度、连续检测的电子传感器居多，其检测信号都是基于电信号[1]，因此该类传感器极易受电磁干扰(electromagnetic interference, EMI)影响，且将其长期置于液体环境中测量会出现参量不稳定等现象[2]。而基于光纤光栅的液体传感器具有抗电磁干扰、耐腐蚀、准分布式测量、实现稳定和准确测量等优点，受到了国内外学者的广泛关注和研究[3-4]。光纤布喇格光栅(fiber Bragg grating, FBG)对应变和温度变化敏感，由于裸光栅易折断，需有效地保护封装后方可应用于工程项目中[5]，但封装在一定程度上阻碍了光栅对外界参量的感知，从而影响传感器的使用场合、测量范围以及测量精度等。因此, 设计实用化且灵敏度高的液体温度与压力双参量传感器成为近年来的研究热点[6-10]。2017年，LIANG等人[11]提出了一种以膜片和悬臂梁为传感单元的光纤光栅压力传感器，该传感器的两个光纤光栅分别粘贴在悬臂梁的上表面和下表面，利用两个光纤光栅的中心波长偏移差作为测量信号，虽然提高了压力测量灵敏度，但该传感器封装不够稳定、易引入应力，且结构复杂不易加工。2020年，VENKATA等人[12]设计并制作了一种膜片式FBG传感器，利用膜片的变形来感知液体的压力，获得液位的变化，然而当被测压力超过一定限度时，膜片就会出现明显的弯曲，光栅粘贴部分的变形较为复杂，测量精度难以保证。2020年，LIU等人[13]将两个光纤光栅以不同的形式封装在聚合物中，根据聚合物在特殊约束条件下浸入液体中的变形原理，可以得到液体中的压力信息，灵敏度得到了较大的提升，但聚合物封装的传感器易老化，且容易出现啁啾现象。
针对上述传感器存在的不足，本文中提出了一种基于光纤光栅的薄壁圆筒式高灵敏度温度与压力传感器，该传感器保留了薄壁圆筒式传感器测量范围大、精度高等优点，克服了灵敏度较低的缺点。通过仿真实验测得，此传感器的压力灵敏度可达153.5pm/MPa，温度灵敏度达31.7pm/℃。该传感器具有低成本、耐腐蚀、可重复性好以及寿命长等特点，在压力和温度测量方面具有应用价值。
1. FBG传感原理
由光源发出的一束光进入光栅后，满足布喇格反射条件的光被反射，该反射光的中心波长为λB，其余光透射过光栅，其作用实质是在光纤中形成一个窄带滤波器[14]。
由耦合模理论可知，满足光纤布喇格条件的光栅反射中心波长为[15]：
λB=2neffΛ (1) 式中，λB为布喇格光栅反射波中心波长，neff为纤芯的有效折射率，Λ为光栅周期。
由(1)式可知，有效折射率和光栅周期是影响反射波中心波长的主要因素。当温度和压力等外界因素发生变化时，导致有效折射率和光栅周期发生变化，从而引起反射波中心波长偏移[16]。温度和应变的变化对FBG中心波长偏移的影响可以表示为[17]：
ΔλBλB=(1−Pe)Δε+(α+ξ)ΔT (2) 式中，ΔλB为反射波中心波长偏移量，Δε为应变变化量，ΔT为外界温度变化量，Pe为有效弹光系数，α和ξ分别为光纤热膨胀系数和热光系数。本文中使用的光纤参量取自普通低损耗单模光纤，其参量初始值如表 1所示。
表 1 Initial values of optical fiber parametersparametric elastic-optic coefficient Pe thermal expansivity α/ (10-6℃-1) thermal coefficient ξ/ (10-6℃-1) wavelength λ/nm 0.22 0.5 6.7 1550 1.1 FBG反射波长与温度的关系
由(2)式可知，在不受到外界应力的影响时，温度变化导致反射波长变化可以表示为：
ΔλBλB=(α+ξ)ΔT (3) 由(3)式和表 1中的参量，可以得到裸光栅的温度系数(即温度灵敏度)为11.2pm/℃。
在工程测量中，该温度灵敏度过低，为了提高灵敏度，可以将裸光栅粘贴在热膨胀系数较大的基底材料上。FBG粘贴在基底材料上，当温度发生变化ΔT时，传感光栅产生的应变为[18]：
εT=(αg−α)ΔT (4) 式中，αg为基底材料的热膨胀系数。此时传感器的波长偏移量为[19]：
ΔλB=λB[(1−Pe)(αg−α)+(α+ξ)]ΔT (5) 由(5)式可知，温度变化时，FBG的波长偏移量不仅与自身热膨胀系数和热光效应有关，而且还与基底材料的热膨胀系数有关[20]。除金属材料作为基底之外，也可以通过聚合物封装FBG来提升传感器温度灵敏度，参考文献[21]和参考文献[22]中分别用环氧树脂和苯偶酰二甲基缩酮(benzil dimethyl ketal, BDK)涂覆封装FBG，实验测得温度灵敏度分别为48pm/℃和149pm/℃，相对于裸光栅而言，两种FBG的灵敏度分别提升了4.3倍和13.3倍。因此, 将光栅粘贴在膨胀系数较大的金属材料或通过聚合物封装后，可以有效提高光栅的温度灵敏度。
1.2 FBG反射波长与压力的关系
当光纤光栅处于稳定的温度场时，如果光栅发生了应变，光栅周期和折射率也会发生变化，从而引起中心波长的偏移可以表示为：
ΔλBλB=(1−Pe)Δε (6) 根据(6)式和表 1中的参量，可得到裸光栅的应变系数为1.2pm/με。
在工程测量时，光栅因其易折断，不能直接用于外界压力的测量，而是需要通过将外界压力转化为封装形变进而引起光栅产生应变来实现对外界压力的实时测量。对于薄壁圆筒封装结构的传感器来说，液体通过进水口进入内筒，筒壁内外两侧形成压差，使粘贴在薄壁上的光栅产生应变，导致光栅的反射波中心波长发生偏移，由广义胡克定律推导得到薄壁圆筒的径向应变ε可表示为[23]：
ε=r2Eh(2−μ)p (7) 式中，E为材料的杨氏模量，μ为材料泊松比，r为内筒半径，h为内筒壁厚度，p为液体压力。由(7)式得出结论：传感器内筒径向应变与内筒半径呈正相关，与内筒壁厚度成反比关系。将(7)式代入(6)式得：
ΔλB=λB(1−Pe)r2Eh(2−μ)p (8) 由(8)式可得出波长偏移量与液体压力的关系：传感器半径越大、内筒厚度越小，材料的杨氏模量越小、泊松比越小，中心波长偏移量就越大，即传感器的压力灵敏度越大。
2. 传感器设计与仿真分析
2.1 传感器设计
为了有效感应液体的温度和压力，需要设计合理的传感器结构，从而将液体的温度和压力转化为光栅的温度和应变，本文中提出了一种薄壁圆筒式传感器，如图 1所示。利用Solidworks软件进行建模，传感器由外壳和内筒两部分构成，传感器外壳长80mm，直径30mm，壁厚1mm；类似“哑铃”形状的内筒由一个薄壁圆筒和位于其两端的柱体组成，液体通过进水孔导入内筒腔，使其发生形变，从而使缠绕并粘贴在内筒壁上的光栅产生应变。同时，液体的温度通过外壳传导至粘贴在导温台的光栅上，实现压力与温度双参量传感。其中，两个光栅串联熔接，根据粘贴于薄壁圆筒的位置不同，分为测压光栅和温补光栅。将光纤从传感结构的右侧尾纤保护套接入，经过通道1后，沿着内筒的外壁紧密缠绕并将测压光栅粘贴于内筒的外壁，光纤再穿过通道2，将温补光栅粘贴在左侧隔绝应力且具有高膨胀系数的导温台上，此处光栅只受温度影响。
2.2 仿真与分析
针对于本传感器的工作环境，传感器的有限元分析主要集中在静态力学分析、结构动力分析、静态热分析等，主要涉及通用的运动方程可以表示为[24]：
\mathit{\boldsymbol{M}} \cdot \mathit{\boldsymbol{x}} + \mathit{\boldsymbol{C}} \cdot \mathit{\boldsymbol{x}} + \mathit{\boldsymbol{K}} \cdot \mathit{\boldsymbol{x}} = \mathit{\boldsymbol{F}}(t) (9) 式中，M是质量矩阵，C是阻尼矩阵，K是刚度系数矩阵，x是位移矢量，F是力矢量。热分析主要研究温度场，通过热分析可以得到不同温度下模型的温度场，进而转变为模型的形变和应变。通用热方程可以表示为：
\mathit{\boldsymbol{c}}\left( \mathit{\boldsymbol{T}} \right) \cdot \mathit{\boldsymbol{T}} + \mathit{\boldsymbol{\kappa }}\left( \mathit{\boldsymbol{T}} \right) \cdot \mathit{\boldsymbol{T}} = \mathit{\boldsymbol{Q}}\left( {t, \mathit{\boldsymbol{T}}} \right) (10) 式中，t是时间，T是温度矩阵，c是比热容矩阵，κ是导热系数矩阵，Q是热流率载荷向量。经过有限元分析可以求得传感器的形变和应变等结果，进而得到传感器的输出特性以及传感器的应变分布，能够为本传感器的灵敏度分析提供数据支撑。
设置内筒的材料、半径、厚度、腔长以及环境温度为变量，在ANSYS Workbench仿真软件中使用静态力学分析等模块对传感器结构进行仿真分析，研究上述变量对传感器压力和温度灵敏度的影响，从而确定传感器结构的各个参量。
仿真过程为：(1)利用Solidworks软件设计该传感器3-D模型；(2)将传感器模型导入到ANSYS Workbench软件；(3)选择静态力学分析模块，设置模型材料，本仿真的材料分别为304不锈钢与铍青铜C17200；(4)设置网格精度进行有限元网格划分；(5)施加载荷并进行求解；(6)通过MATLAB软件对所有仿真结果进行图像绘制并分析。
2.2.1 传感器内筒材料的选择
考虑到传感器需在液体中长期工作，初步选择耐腐蚀性良好的304不锈钢和铍青铜C17200作为传感器材料，相关参数如表 2所示。
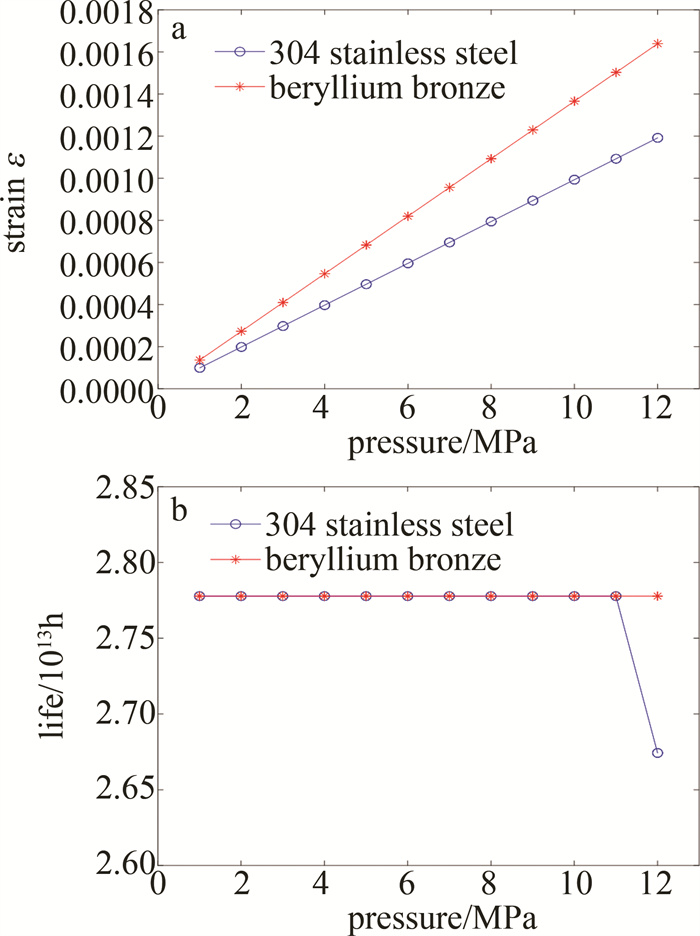
表 2 The related parameters of materialmaterials elasticity modulus E/GPa Poisson’s ratio μ thermal expansivity α/(10-6℃-1) 304 stainless steel 190 0.3 16 beryllium bronze 134 0.275 17.6 为了研究两种不同材质内筒的应变的变化量，对传感器内筒进行应变仿真。将环境温度设置为40℃，选用厚度均为0.5mm的304不锈钢与铍青铜C17200材质的传感器内筒，在其内壁施加1MPa~12MPa的压力载荷，对数据进行线性拟合，得到径向应变与压力的关系如图 2a所示。由图 2a可知，在厚度一定的情况下，随着压力的增大，内筒壁径向应变呈现线性增大趋势，经拟合后得到304不锈钢材质的传感器应变的变化量为99.3με/MPa，铍青铜C17200材质的传感器应变的变化量为136.6με/MPa，故铍青铜C17200材质的内筒径向应变更灵敏。
![图 2 Relationship between sensor performance and pressure]()
图 2 Relationship between sensor performance and pressurea—relationship between strain and pressure variation b—relationship between life and pressure variation为了检验本传感器在不同压强下的最长工作时间，对传感器内筒进行寿命仿真。寿命含义为该结构在低于静态极限强度载荷的重复载荷作用下，出现断裂破坏现象的时间。该传感器的寿命是通过ANSYS Workbench软件中静态力学分析模块的疲劳工具仿真得到，以美国机械工程师协会(American Society of Mechanical Engineers, ASME)锅炉和压力容器规范(ASME boiler and pressure vessel code)作为计算依据。由于传感器内筒疲劳损伤具有随机性和不可逆的特点，总损伤量是若干次损伤量的线性累加，采用Miner累积疲劳准则，最终完成内筒寿命的预测。在累计疲劳准则中，材料失效的临界疲劳损伤D=1，当不同载荷施加到传感器内筒壁上时其疲劳寿命会发生变化，随着使用时间的增加，疲劳累计损伤可以表示为：
D = \sum\limits_{i = 1}^I {\frac{{{n_i}}}{{{N_i}}}} = \frac{{\sum\limits_{i = 1}^I {{W_i}} }}{W} (11) 式中，I为疲劳损伤次数，ni为不同负载的循环次数，Ni为不同负载下应力循环次数，Wi为不同负载下吸收的能量值，W为失效总能量。
在疲劳工具模块中应选择应力疲劳的分析方式，选用厚度均为0.5mm的304不锈钢与铍青铜C17200材质的薄壁圆筒，在其内壁施加1MPa~12MPa的压力载荷，分析两种材质内筒结构在不同压强下最长工作时间。对寿命仿真数据进行拟合，得到图 2b所示的寿命与压力的变化关系。由图 2b可知，当压力载荷施加大于11MPa(等效于水下1100m)时，304不锈钢材质的内筒寿命突减，说明此时传感结构已受到破坏，不能正常工作，但当304不锈钢材质的内筒壁厚改为0.6mm时，传感器寿命在大于11MPa不再发生突变。因此，改变传感器的内筒材料和壁厚度便可以改变灵敏度和测量范围，以适应不同的测量环境和要求。
2.2.2 传感器内筒半径的选择
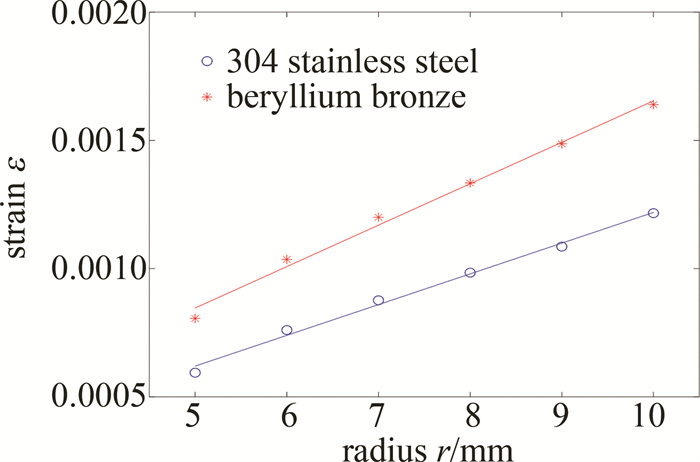
将环境温度设置为40℃、内筒材料分别设置为304不锈钢和铍青铜C17200，固定内筒壁厚度和内筒腔长不变，对内筒半径取不同值进行仿真，探究内筒半径对径向应变的影响。考虑到传感器的尺寸不宜过大，故半径范围从5mm以1mm为步长增加到10mm，对内筒壁施加12MPa的压力载荷。对数据进行线性拟合，得到径向应变与内筒半径的关系如图 3所示。
由图 3可知，在内筒壁厚度和内筒腔长固定不变的情况下，随着内筒半径的增大，应变呈线性增大，仿真数据拟合结果与(7)式的结论一致，且铍青铜C17200材质的内筒应变更灵敏。在筒壁弹性形变可恢复范围内，为了寻求更高灵敏度, 可以将内筒半径设置得更大一些，但是传感器外壳的尺寸又直接限制了内筒半径不可能过大。综合考虑，传感器内筒半径选取为10mm。
2.2.3 传感器内筒壁厚的选择
内筒壁厚度会影响传感器的灵敏度，厚度太大会导致灵敏度过低，厚度太小会导致传感器在高压状态下不能长期工作，所以厚度直接关系到灵敏度大小与传感器工作寿命长短。为了寻找内筒壁厚的最优值，内筒材料分别设置为304不锈钢和铍青铜C17200，在内筒半径和内筒腔长不变的情况下，环境温度设置为40℃，对内筒厚度进行调整，范围从0.5mm~1.0mm，步进为0.1mm，对内筒壁施加12MPa的压力载荷，分析内筒壁厚对径向应变的影响。通过对数据进行二次拟合，得到径向应变与内筒壁厚的关系如图 4所示。
由图 4可知，在内筒半径和内筒腔长固定不变的情况下，随着厚度不断增大，两种材质的内筒应变与厚度均呈现负相关，且逐渐趋于平缓，仿真数据拟合结果与(7)式的结论相符，但铍青铜C17200材质的内筒应变更灵敏。根据图 2b可知，厚度为0.5mm时，304不锈钢材质的内筒长期工作在12MPa下，寿命明显小于铍青铜C17200材质的传感器。由此可见，当内筒材料为304不锈钢时，壁厚应选择0.6mm；当内筒材料为铍青铜C17200时，壁厚应选择0.5mm。
2.2.4 传感器内筒腔长度的选择
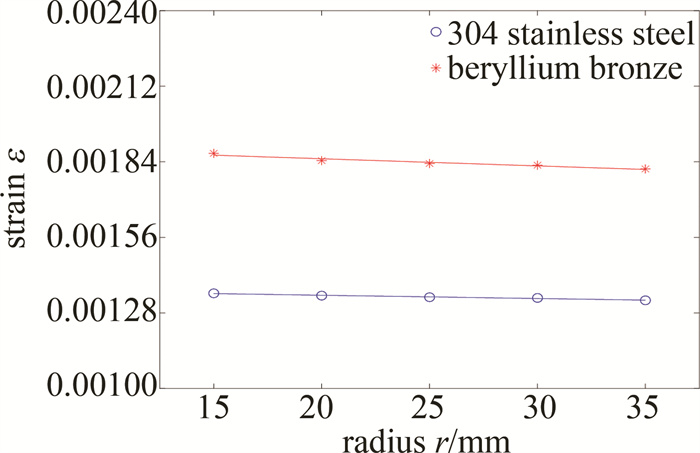
在内筒壁厚度和内筒半径不变的情况下，改变内筒腔长度取值，长度范围由15mm以5mm为步长增加到35mm。内筒材料分别设置为304不锈钢和铍青铜C17200，环境温度设置为40 ℃，对内筒壁施加12MPa的压力载荷。对数据进行拟合，得到径向应变与内筒腔长度的关系如图 5所示。
由图 5可知，在内筒半径和内筒壁厚固定不变的情况下，随着腔长不断增大，两种材质的内筒应变变化不明显，故内筒腔长的变化不会对应变造成影响，仿真数据拟合结果与(7)式所得结论一致。在应变相同的情况下，选择较长腔长的内筒，便于光纤缠绕与光栅的粘贴，但传感器整体结构又限制了内筒腔长不宜过长。因此，传感器内筒腔长应为30mm。
2.3 仿真结果与误差分析
2.3.1 仿真结果
结合以上仿真结果，当传感器内筒半径为10mm、长度为30mm、内筒材料选择304不锈钢时，内筒壁厚度为0.6mm; 当材料选择铍青铜C17200时，内筒壁厚度为0.5mm。若传感器采用0.6mm的304不锈钢内筒时，由表 2可知，杨氏模量E=190GPa，泊松比μ=0.3，代入(8)式可得测压光栅的理论压力灵敏度为108pm/MPa；若传感器采用0.5mm的铍青铜C17200内筒时，由表 2可知，E=134GPa，泊松比μ=0.275，代入(8)式可得测压光栅理论压力灵敏度为155pm/MPa。
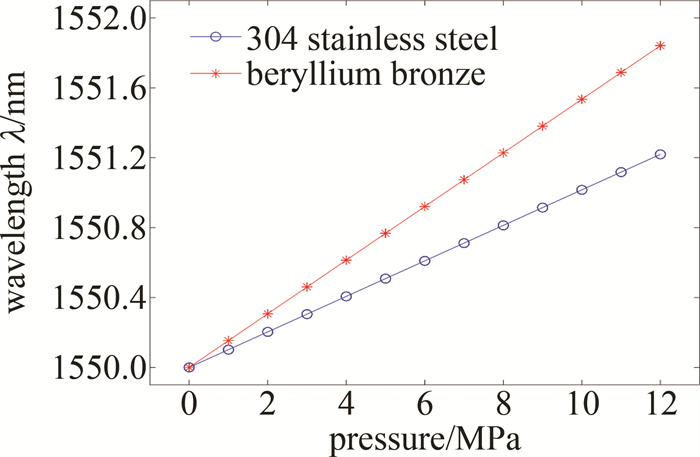
图 6所示为光栅的反射波长随压力变化曲线。由图 6可知，反射波长与压力呈现良好的线性关系。当内筒材料选择304不锈钢时，仿真压力灵敏度为101.6pm/MPa；当内筒材料选择铍青铜C17200时，仿真压力灵敏度为153.5pm/MPa，相较于裸光栅的压力灵敏度3pm/MPa[25]分别提升33.9倍和51.2倍。
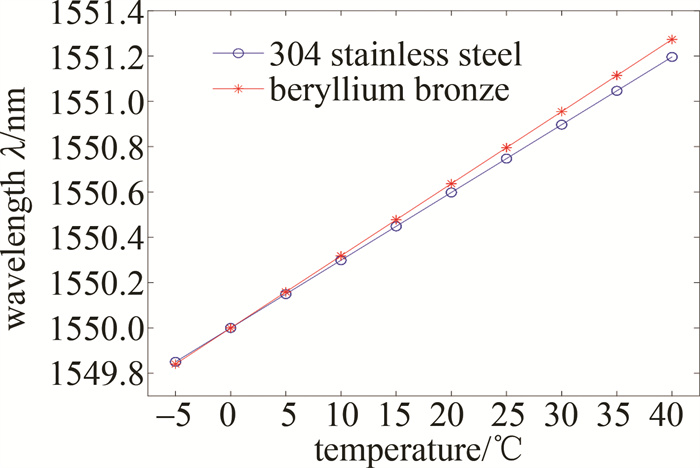
由表 2可知，304不锈钢和铍青铜C17200的热膨胀系数分别为16×10-6/℃和17.6×10-6/℃，根据(5)式可以得到两种材质的传感器温度灵敏度分别为29.9pm/℃和31.8pm/℃。对两种材质传感器进行温度灵敏度分析，温补光栅在不受任何应变的情况下，对外界温度进行调整，范围-5℃~40℃，步进为5℃，温补光栅区域反射波长随温度的变化如图 7所示。
由图 7可知，测温光栅反射波长随温度变化呈现良好的线性关系，当传感器材料采用304不锈钢时，温度灵敏度可达30pm/℃，约为裸光栅的2.6倍；当传感器材料采用铍青铜时，温度灵敏度可达31.7pm/℃，约为裸光栅的2.8倍。
2.3.2 误差分析
本传感器的压力和温度仿真灵敏度与(5)式和(8)式计算得到的压力和温度理论灵敏度对比可知，当传感器内筒材料为304不锈钢时，压力灵敏度的相对误差为5.92%，温度灵敏度的相对误差为0.33%；当传感器内筒材料为铍青铜C17200时，压力灵敏度的相对误差为0.96%，温度灵敏度的相对误差为0.31%。针对304不锈钢材质的传感器压力灵敏度误差较大的问题，经过反复验证得出结论：在有限元分析时，对同一个模型进行不同大小网格划分以及不同形状网格划分时，会对仿真结果产生一定影响，将网格缩小至1.8mm时，压力灵敏度的相对误差能够从5.92%降至0.04%；对于温度灵敏度的误差是由于随着温度的变化，金属材料会产生微小形变，进而对波长造成微小影响。
3. 结论
为了解决现有光纤光栅液体双参数传感器灵敏度低等问题，结合光栅传感原理，利用Solidworks软件对传感器建模，使用仿真软件系统地分析了传感器内筒各个参量对传感特性的影响，为传感器的制备提供了理论基础。结果表明，使用304不锈钢材料封装的传感器压力灵敏度可以达到101.64pm/MPa，温度灵敏度可以达到30pm/℃；使用铍青铜C17200材料封装的传感器压力灵敏度可以达到153.5pm/MPa，温度灵敏度可以达到31.7pm/℃，并对结果存在的误差进行了评估。更重要的是，改变该传感器的内筒材料和尺寸便可以改变灵敏度和测量范围，以适应不同的测量环境和要求。这种双参量传感器在石油开采和海洋勘探等复杂环境领域有许多潜在的准分布测量应用，在液体压力和温度测量方面具有应用价值。
-
![]()
图 2 Relationship between sensor performance and pressure
a—relationship between strain and pressure variation b—relationship between life and pressure variation
表 1 Initial values of optical fiber parameters
parametric elastic-optic coefficient Pe thermal expansivity α/ (10-6℃-1) thermal coefficient ξ/ (10-6℃-1) wavelength λ/nm 0.22 0.5 6.7 1550 
下载: 导出CSV
表 2 The related parameters of material
materials elasticity modulus E/GPa Poisson’s ratio μ thermal expansivity α/(10-6℃-1) 304 stainless steel 190 0.3 16 beryllium bronze 134 0.275 17.6
下载: 导出CSV
-
[1] PALASAGARAM J N, RAMADOSS R. Liquid crystal polymer-based MEMS capacitive pressure sensor[J]. Proceedings of the SPIE, 2005, 5798: 190-197. DOI: 10.1117/12.606642
[2] LI Ch, ZHANG Ch, LI J, et al. Liquid level and temperature sensor based on an asymmetrical fiber Mach-Zehnder interferometer combined with a fiber Bragg grating[J]. Optics Communications, 2016, 372: 196-200. DOI: 10.1016/j.optcom.2016.04.025
[3] MAJUNDER M, GANGOPADHYAY T K, CHAKRABORTY A K, et al. Fiber Bragg gratings in structural health monitoring—Present status and applications[J]. Sensors and Actuators, 2008, A147(1): 150-164.
[4] MIHALOVS J. Fiber Bragg grating sensors for harsh environments[J]. Sensors, 2012, 12(12): 1898-1918.
[5] JASJOT K S, NEENA G, DIVYA D, et al. Fiber Bragg grating sensors for monitoring of physical parameters: A comprehensive review[J]. Optical Engineering, 2020, 59(6): 060901.
[6] WOYESSA G, PEDERSEN JKM, NIELSEN K, et al. Enhanced pre-ssure and thermal sensitivity of polymer optical fiber Bragg grating sensors[J]. Optics & Laser Technology, 2020, 130: 106357.
[7] LIANG M F, FANG X Q, NING Y S. Temperature compensation fiber Bragg grating pressure sensor based on plane diaphragm[J]. Photonic Sensors, 2018, 8(2): 157-167. DOI: 10.1007/s13320-018-0417-9
[8] FAN Q G, ZHEN A J, FENG D Q, et al. Highly sensitive FBG pressure sensor based on square diaphragm[J]. Optik—International Journal for Light and Electron Optics, 2021, 225: 165559. DOI: 10.1016/j.ijleo.2020.165559
[9] VORATHIN E, HAFIZI Z M, AIZZUDDIN A M, et al. A natural rubber diaphragm-based transducer for simultaneous pressure and temperature measurement by using a single FBG[J]. Optical Fiber Technology, 2018, 45: 8-13. DOI: 10.1016/j.yofte.2018.05.011
[10] ZHAO L J, ZHAO H Y, XU Zh N. Design of high-sensitivity hydrostatic pressure sensor based on Brillouin dynamic grating[J]. Acta Photonica Sinica, 2021, 50(2): 206001(in Chinese).
[11] LIANG M F, FANG X Q, WANG G, et al. A fiber Bragg grating pressure sensor with temperature compensation based on diaphragm-cantilever structure[J]. Optik—International Journal for Light and Electron Optics, 2017, 145: 503-512. DOI: 10.1016/j.ijleo.2017.08.014
[12] VENKATA S C S V, SAIDI R P, SANJEEV A, et al. Design and development of pressure sensor based on fiber Bragg grating (FBG) for ocean applications[J]. The European Physical Journal-Applied Physics, 2020, 90: 30501. DOI: 10.1051/epjap/2020200036
[13] LIU M Y, WU Y B, DU C R, et al. FBG based liquid pressure sensor for distributed measurement with a single channel in liquid environment[J]. IEEE Sensors Journal, 2020, 20(16): 9155-9161. DOI: 10.1109/JSEN.2020.2986550
[14] UMA K C R, DHANALAKSHMI S, KUMAR R, et al. Development and experimental validation of a nuttall apodized fiber Bragg grating sensor with a hydrophobic polymer coating suitable for monitoring sea surface temperature[J]. Optical Fiber Technology, 2020, 56: 102176. DOI: 10.1016/j.yofte.2020.102176
[15] GAO X K, NING T G, ZHANG CH B, et al. A dual-parameter fiber sensor based on few-mode fiber and fiber Bragg grating for strain and temperature sensing[J]. Optics Communications, 2020, 454: 124441. DOI: 10.1016/j.optcom.2019.124441
[16] ZHU L Q, YANG R T, ZHANG Y M, et al. Metallic-packaging fiber Bragg grating sensor based on ultrasonic welding for strain-insensitive temperature measurement[J]. The Review of Scientific Instruments, 2018, 89(4): 045005. DOI: 10.1063/1.5002745
[17] LIU W L, GUO Y X, XIONG L, et al. Fiber Bragg grating based displacement sensors: State of the art and trends[J]. Sensor Review, 2019, 39(1): 89-98.
[18] WU H, LIN Q J, JIANG Zh D, et al. A temperature and strain sensor based on a cascade of double fiber Bragg grating[J]. Measurement Science and Technology, 2019, 30(6): 065104. DOI: 10.1088/1361-6501/ab093e
[19] ZHANG D P, WANG J, WANG Y J. Experimental study on fiber Bragg grating temperature sensor and its pressure sensitivity[J]. International Journal of Information and Communication Technology, 2018, 13(4): 509-517. DOI: 10.1504/IJICT.2018.095034
[20] KUANG Y, GUO Y X, XIONG L, et al. Packaging and temperature compensation of fiber bragg grating for strain sensing: A survey[J]. Photonic Sensors, 2018, 8(4): 320-331. DOI: 10.1007/s13320-018-0504-y
[21] UMESH S, DAEGIL K, HYUNJIN K, et al. Polymer-coated FBG sensor for simultaneous temperature and strain monitoring in composite materials under cryogenic conditions[J]. Applied Optics, 2018, 57(3) : 492-497. DOI: 10.1364/AO.57.000492
[22] CHENG X Sh, QIU W W, WU W X, et al. High-sensitivity temperature sensor based on Bragg grating in BDK-doped photosensitive polymer optical fiber[J]. Chinese Optics Letters, 2011, 9(2) : 020602. DOI: 10.3788/COL201109.020602
[23] HUANG H Y. Fabrication and evaluation of hybrid silica/polymer optical fiber sensors for large strain measurement[J]. Transactions of the Institute of Measurement and Control, 2009, 31(3/4): 247-257.
[24] ZHAO G F. Theory of structural reliability[M]. Beijing: China Architecture and Building Press, 2000: 5-6 (in Chinese).
[25] LI Y Q, GUO W, XIE Y. Temperature and strain characteristics of fiber Bragg grating packaged by brass slice[C]//2010 International Conference on Measuring Technology and Mechatronics Automation. New York, USA: IEEE, 2010: 734-737.
-
期刊类型引用(4)
1. 吕子尚，胡劲华，任丹萍，赵继军. 平顶型CLPG-CFBG级联结构中温度应力传感特性的研究. 激光技术. 2024(01): 65-70 . 
本站查看
2. 张白莉，高震森，郭红英. 基于FBG的高温压力传感器设计与校准. 半导体光电. 2024(04): 561-567 . 百度学术
3. 郭煜恩，谭跃刚，吕文强. 双F-P型高温/应变复合光纤传感器. 传感技术学报. 2023(02): 198-203 . 百度学术
4. 龚文慧，张雄星，康家雯. 级联FPI-MZI复合干涉光纤传感器双参数特性研究. 激光技术. 2022(05): 618-623 . 本站查看
其他类型引用(1)
计量
- 文章访问数: 7
- HTML全文浏览量: 1
- PDF下载量: 7
- 被引次数: 5