Advances of rare earth ions doped solid-state quantum memory at telecom band
-
摘要: 量子互联网是实现多方量子通信、分布式量子计算等量子信息技术的重要基础,量子存储器作为实现互联网的重要部件,对量子信息技术的发展、应用具有举足轻重的作用。如今遍布全球的光纤网络已经是信息传输的有力载体,通信波段的量子存储器因容易嵌入到当前的光纤网络中而备受重视。聚焦于稀土离子掺杂固态体系的通信波段光量子存储,首先介绍稀土离子掺杂固态量子存储的基本原理,包括稀土掺杂材料特性以及存储协议等,然后介绍目前的研究现状,最后简要分析其未来的发展趋势,并对量子互联网的构建做出展望。Abstract: Quantum internet is an important basis for realizing multi-party quantum communication, distributed quantum computing, and other quantum information technologies. Quantum memory, as a significant part for realizing Internet, plays a pivotal role in the development and application of quantum information technology. Nowadays, the global optical fiber network has become a powerful carrier of information transmission, and quantum memory in communication band is highly valued because it is easy to be embedded in the current optical fiber network. Focus on telecom band optical quantum memory with rare earth ions doped solid-state system, the basic principle of rare earth ions doped solid-state quantum memory was firstly introduced, including rare earth doped material properties and memory protocol. the current state of the art was then introduced. Finally, a brief analysis on its future development trend was given, and the prospect for the construction of quantum Internet was made.
-
Keywords:
- quantum optics /
- telecom band /
- solid-state quantum memory /
- rare earth ions
-
引言
光声成像是过去20年来新兴的一种生物医学成像模态[1-6],它是一种光激发的混合成像模式,将光学成像和超声成像的优点结合了起来。一方面,在光声成像中用来重建图像的信号是超声信号,生物组织对超声信号的散射要比光学信号低2~3个数量级,因此相比纯光学成像,光声成像具有更深的成像深度和更高的空间分辨率;另一方面,光声成像根据不同组织对可见光、近红外光的选择性吸收,利用特定波长的激光脉冲对组织进行照射,成像的是在生物组织内被吸收的激光脉冲能量的分布,其一定程度上反映组织的吸收系数分布,这在纯超声成像中是无法做到的,因此相比纯超声成像,光声成像具有更高的光学对比度。
目前光声成像系统逐步向实时[7-9]、多维度[10-11]方向发展,因此采用单通道、单超声换能器系统由于存在系统鲁棒性差,需进行多次调整,单切面扫描时间过长等问题已不能够适应最新的发展趋势,所以必须研发能够高速多通道采集光声信号的高鲁棒性光声成像系统。而国际上已有很多开展在体光声断层成像方面的研究[12-21], 这些研究中成像系统的实现方式和目的各有不同,有的采用线性阵列[12, 15-17],有的主要开展离体的成像实验[13-14]; 参考文献[18]中主要针对光声显微成像方面; 参考文献[19]中采用的是一个垂直放置的弧形的换能器阵列,需要旋转成像对象才能获得3维的图像; 参考文献[20]和参考文献中采用弧形换能器阵列开展实时在体实验,但是由于其激光是垂直激发成像对象即正交模式,所以只适合小动物脑部成像,不适合断层成像;参考文献[7]和参考文献[8]中专门设计用于开展临床实验。因此本文中采用背向传输模式, 即超声换能器阵列与脉冲激光在同一侧, 这样就保证了在成像不同断层时不会对成像对象带来影响, 同时利用美国国家仪器公司(Naticmal Instruments, NI)的数据采集模块和多通道弧形聚焦换能器来构建多通道采集模块以实现光声断层成像数据的高速采集, 最后利用正则化优化的基于模型的重建算法对原始数据进行高质量的图像重建。
1. 理论分析
1.1 光声成像前向模型
光声信号的产生是由于短时脉冲激光照射生物组织,组织中的吸收体吸收一部分能量使得局部温度升高,导致发生热弹性膨胀,从而产生超声波。在满足热力限制和应力限制的条件下,声压p(r, t)满足的关系[22]:
\begin{array}{l} \frac{{{\partial ^2}p(\mathit{\boldsymbol{r}}, t)}}{{\partial {t^2}}} - {c^2}\left( \mathit{\boldsymbol{r}} \right)\rho \left( \mathit{\boldsymbol{r}} \right)\nabla \cdot \\ \left[ {\frac{1}{{\rho \left( \mathit{\boldsymbol{r}} \right)}}\nabla p(\mathit{\boldsymbol{r}}, t)} \right] = \mathit{\Gamma }\frac{{\partial H(\mathit{\boldsymbol{r}}, t)}}{{\partial t}} \end{array} (1) 式中,r为3维空间内的位置坐标; t表示时间; c(r)和ρ(r)分别为组织的声速和密度; Γ为无量纲格鲁内森参量; H(r, t)是热源函数,代表单位时间、单位体积内的热量。假设生物组织的密度是均匀的,即在成像区域内ρ(r)是常数,并假设声速是均匀的,即c(r)为常数c,另外热源函数还可以表示为H(r, t)=H(r)×H(t),其中H(r)表示单位体积内沉积的热能量,H(t)表示脉冲激光光强随时间的分布函数。在实际成像过程中脉冲激光脉宽很短,理论上光强函数可假设为一个脉冲函数,即H(t)=δ(t),因此(1)式可表示为:
\frac{{{\partial ^2}p(\mathit{\boldsymbol{r}}, t)}}{{\partial {t^2}}} - {c^2}{\nabla ^2}p(\mathit{\boldsymbol{r}}, t) = \mathit{\Gamma }H\left( \mathit{\boldsymbol{r}} \right)\frac{{\partial \delta \left( t \right)}}{{\partial t}} (2) (2) 式可以等价地表示为一个初始值问题:
\frac{{{\partial ^2}p(\mathit{\boldsymbol{r}}, t)}}{{\partial {t^2}}} - {c^2}{\nabla ^2}p(\mathit{\boldsymbol{r}}, t) = 0 (3) 初始条件为:
\left\{ \begin{array}{l} p(\mathit{\boldsymbol{r}}, t)\left| {_{t = 0} = \mathit{\Gamma }H\left( \mathit{\boldsymbol{r}} \right)} \right.\\ \frac{{\partial p(\mathit{\boldsymbol{r}}, t)}}{{\partial t}}\left| {_{t = 0} = 0} \right. \end{array} \right. (4) 上述初始值问题可以通过求解一个泊松类型的积分[23]而得到一个解析解:
p(\mathit{\boldsymbol{r}}, t) = \frac{\mathit{\Gamma }}{{4{\rm{ \mathit{ π} }}c}}\;\frac{\partial }{{\partial t}}\int_{S'\left( {\mathit{\boldsymbol{r}}, t} \right)} {\frac{{H\left( {\mathit{\boldsymbol{r'}}} \right)}}{{\left| {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{r'}}} \right|}}} {\rm{d}}S'(\mathit{\boldsymbol{r}}, t) (5) 式中,积分的对象是一个半径为|r-r′|=ct的球形表面S′(r, t),在2维平面即断层平面,所有的光声信号源和测量点位于同一平面,此时积分是沿着半径为|r-r′|=ct的圆周L′(t)开展,忽略(5)式中的常数,光声断层成像的前向模型可表示为:
p(\mathit{\boldsymbol{r}}, t) = \frac{\partial }{{\partial t}}\int_{L'\left( t \right)} {\frac{{H\left( {\mathit{\boldsymbol{r'}}} \right)}}{{\left| {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{r'}}} \right|}}} {\rm{d}}L'(t) (6) 1.2 基于模型的逆向重建
光声断层重建算法主要分为3种:第1种是基于雷登变换的滤波反投影重建算法; 第2种是基于时间反转方法的重建算法; 第3种是基于模型的重建算法。滤波反投影算法虽然实现容易且重建速度很快,但是其重建图像含有条状伪影而影响图像质量。时间反转方法虽然通过反向模拟超声波传播来得到更好质量的重建图像,但是这个过程需要复杂的数值仿真,不适合实时成像的要求。而基于模型的重建算法是在采集的声压信号数据和组织的吸收分布之间建立一种线性映射关系,继而通过最优化方法去最小化采集的声压信号与利用模型计算的声压信号之间的误差。因而具有很强的灵活性,且模型矩阵只与所使用的图像网格和信号采集系统的参量有关,而与实际的成像对象无关。
在基于模型的光声断层重建算法中,第1步是计算模型矩阵,需要用到导数的数值近似表示,因此(6)式可近似表示为:
p(\mathit{\boldsymbol{r}}, t) \approx \frac{{I\left( {\mathit{\boldsymbol{r}}, t\Delta t} \right) - I\left( {\mathit{\boldsymbol{r}}, t - \Delta t} \right)}}{{2\Delta t}} (7) 式中, 采用的是导数的中间差分近似。I(r, t)为:
I\left( {\mathit{\boldsymbol{r}}, t\Delta t} \right) = \int_{L'\left( t \right)} {\frac{{H\left( {\mathit{\boldsymbol{r'}}} \right)}}{{\left| {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{r'}}} \right|}}} {\rm{d}}L'(t) (8) 第2步就是计算(8)式,方法有很多[24-25]。最后(8)式和(9)式可以表示为:
\mathit{\boldsymbol{p}} = \mathit{\boldsymbol{Ax}} (9) 式中,p∈Rm为向量化表示的超声换能器阵元采集到的声压信号, x∈Rn为向量化表示的吸收分布,也即初始声压分布,A∈Rm×n是模型矩阵或系统矩阵,表示一个线性算子描述组织的光学吸收分布与换能器探测的声压信号数据之间的关系。
基于模型的重建算法可以分为两类,第1类是通过求解(10)式最小二乘问题的算法,成为朴素算法,其解称为朴素解:
{\mathit{\boldsymbol{x}}_{{\rm{native}}}} = \mathop {{\rm{argmin}}}\limits_x \left\| {\mathit{\boldsymbol{p}} - \mathit{\boldsymbol{Ax}}} \right\|_2^2 (10) 式中,xnaive为最终求解的朴素解。
第2类算法为基于正则化的算法,由于基于模型的光声断层图像重建问题通常是病态的,因此朴素解与精确解之间通常有较大的偏离,为了获得更好的近似解,需要使用各种正则化项,比如Tikhonov正则化、稀疏正则化、全变分正则化等。
2. 系统实现
2.1 硬件系统
整个系统的硬件组成示意图如图 1所示。光声断层成像系统的激发脉冲激光器采用的是德国INNOLAS公司生产的掺钕钇铝石榴石(Nd: YAG)激光器,该激光器分成两部分:前部分为抽运源,抽运波长为532nm,输出能量为400mJ,重复频率为10Hz,脉冲宽度为4ns~8ns; 后部分为光学参量振荡器(optical parametric oscillator, OPO)可调谐激光器,波长调谐范围为680nm~960nm的红光及近红光波段,在750nm时,输出能量超过80mJ。其余还有耦合透镜、耦合光纤和10根光线束。
超声换能器采集硬件局部放大图如图 2a所示。超声换能器采用的是法国IMASONIC公司的定制中心频率是5MHz,带宽为80%,覆盖角度为270°的128阵元弧形聚焦换能器,结构图如图 2b所示,每个阵元的结构图如图 3a所示。聚焦的半径为40mm,阵元的高度为15mm,相邻阵元之间的间隔为0.1mm。在成像水箱中,通过一个具有四肢的夹具把换能器夹住,使之水平放置。而换能器夹具的上下面各有5个可以放置耦合光纤端头的楔形槽,上面5个楔形槽均匀分割整个圆周,下面的5个楔形槽与上面相应位置的楔形槽堆成,且每个楔形槽与水平放置的换能器成一定角度,而每一个耦合光纤端头把耦合进来的激光整形为线光源,这样就把线光源均匀地照射到换能器的聚焦平面内。
如图 2a所示,成像小鼠通过悬挂臂支撑系统垂直固定,在实际在体的成像试验中,小鼠先涂上超声耦合胶,之后体表面覆盖一层薄膜与水隔离,最后在小鼠嘴部通过麻醉系统设置好麻醉。竖直的悬挂臂被固定在水平横梁上,而水平横梁与机械垂直升降台融为一体通过直线电机如图 1所示。这里采用直线电机是为了减少电磁干扰对采集系统的噪声影响。之后机械垂直升降台通过直线电机的上下运动来达到控制成像小鼠采集不同的断层切片。图 3b中描绘了此超声换能器仿真的声场图。可以看到, 成像平面是一个直径近似为20mm、厚度为0.7mm的圆盘,此圆盘切片保证了系统在进行断层成像时的特异性。
超声换能器采集的128通道超声信号通过基于NI的采集模块进行处理。具体是工控机机箱采用的是NI的配有8个插槽和高带宽背板的PXIe-1082,每个插槽都可以插入PXI Express模块,且含有一个系统定时同步插槽。主机采用的是NI的基于Intel core i7-3610QE处理器的高性能嵌入式控制器PXIe-8135, 负责协调整个采集过程,这样就不用在需要额外的计算机。定时和同步模块采用的是NI的PXIe-6674T, 用于同步脉冲激光器触发信号和多通道采集模块。采集处理模块采用的是NI FlexRIO硬件,其为NI LabVIEW现场可编程门阵列(field-programmable gate array, FPGA)提供灵活且可定制的I/O。此硬件包含两部分,分别是4个FPGA模块PXIe-7965R和4个提供高性能模拟和数字I/O的适配器模块NI 5752。NI 5752为32通道数字化适配器模块,分辨率为12位,采样频率为50MS/s,另外还含有抗混叠滤波器和可编程时变增益控制,这样就可以在模数转换过程中对微弱的光声信号进行高频滤波和增益放大,以增大信号的信噪比。这两部硬件共同构成一个可重新配置的子系统,通过LabVIEW FPGA软件进行编程。
2.2 软件系统
整个采集系统的软件流程图如图 4所示。
首先, 脉冲激光器的同步触发信号给到PXIe-6674T,之后同步FlexRIO硬件采集数据,每个通道采集的数据会以一个一个64位的先进先出(first-in and first-out, FIFO)的数据结构通过直接内存访问(direct memory access, DMA)传输到内存,不需要经过控制器干预,然后再对数据进行处理,处理的数据可以一边进行实时显示,一边存储到硬盘进行后期重建。采集系统的前面板界面如图 5所示。
3. 成像实验
为了对整个光声断层成像系统进行验证,首先进行了系统的空间分辨率验证实验。利用水笔芯进行成像,水笔芯的内壁厚度为90mm,图 6a为成像结果图中通过水笔芯圆心的整个水平像素点特性曲线,图 6b为第2个峰值信号的局部放大图。在该峰值的一半处宽度测量为200μm,根据参考文献[26]中所述方法,一般来说,成像对象的大小近似为该物体真实大小和系统空间分辨率大小的平方和的平方根,即2002=902+r2,其中r为空间分辨率,所以该系统的空间分辨率约为180μm。
之后进行了离体成像实验。离体的实验对象是一个柱状模拟样品,用5%的琼脂粉和80%的去离子水经过搅拌均匀加热到透明状的液体后,再冷却到常温后加入15%的脂肪乳搅拌均匀,之后取一柱状容器,容器内固定两个六边形柱体模具,间隔为5mm,最后把混合液倒入容器内凝固形成一含有两个六边形柱体模具空腔的模拟样品仿体,再在空腔内注射黑色墨水,进行断层成像。激发波长为750nm,每次断层采集平均20次用于对原始数据进行去噪,一次采集长度为2600个点,图 7a为超声换能器第1个阵元采集的原始光声信号曲线。可以看到, 除有效信号外,噪声的幅值很小,这也说明了该光声断层成像采集系统具有很好的噪音抑制能力。重建算法采用的是正则化优化的基于模型的光声重建算法,结果图如图 7b所示。图像像素个数为256×256,每个像素的大小为0.1mm。可以看出, 重建结果中断层截面上两个六边形非常清楚。
![Figure 6. a—characteristic curve of horizontal pixel point in the reconstruction result of pen core b—partial enlargement of the second peak signals of Fig. 6a]() Figure 6. a—characteristic curve of horizontal pixel point in the reconstruction result of pen core b—partial enlargement of the second peak signals of Fig. 6a
Figure 6. a—characteristic curve of horizontal pixel point in the reconstruction result of pen core b—partial enlargement of the second peak signals of Fig. 6a最终成像系统是为了能够开展小动物在体实验,所以又进行了在体小动物成像实验。实验对象为6周的BALB/c雄性裸鼠,在裸鼠体表涂上超声耦合胶用来保证声速的匹配,之后通过薄膜包裹保证实验中与水隔离。再把裸鼠嘴部接入异氟烷和氧气混合的麻醉气体,最后固定在小鼠固定支架上,激发波长为750nm,采集点数和采集平均次数分别为20和2600。通过控制直线电机的运动来采集裸鼠不同的断层数据。重建算法采用的是正则化优化的基于模型的光声重建算法,结果图如图 8b所示。可以看到,小鼠的肝部和脊柱都非常清晰,且重建图像内部非常均匀,伪影很少,另外裸鼠的皮肤与内脏的边界也很清晰,图 8a是裸鼠在该成像位置对应的组织切片图。重建图像的结果与组织切片图很吻合。图像像素个数为256×256,每个像素的大小为0.1mm。该试验很好地验证了该断层成像系统可以用来开展在体的小动物光声断层成像研究。
4. 结论
模拟样品和小鼠在体的成像实验结果均表明, 该断层成像系统可以用于开展小动物光声断层成像实验研究。另外该断层成像系统在采集一个断层数据且采集平均次数为20次时所耗费的时间为1.04ms,正则化优化的基于模型的光声重建算法在重建一个断层的数据且重建图像像素个数为256×256时所消耗的时间为40s左右,其中30s为系统矩阵的计算,剩余10s为重建图像的迭代计算。所以该断层成像系统可以高速采集断层数据,近实时地进行高质量的图像重建。后期计划对算法进行图形处理器加速以进一步缩短重建时间,使之达到实时。另外由于脉冲激光器为可调谐激光器,波长在红光和近红外波段连续可变,所以还可以进行多光谱成像,进而对组织中的血红蛋白和光声造影剂进行光谱分离,以提升该系统的科研应用价值。
-
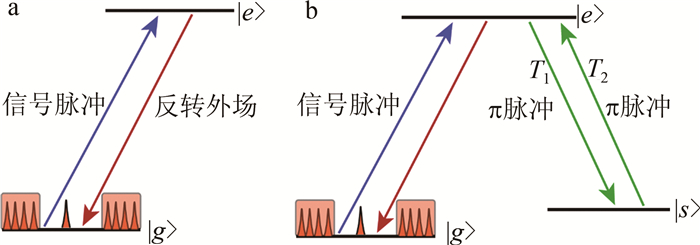
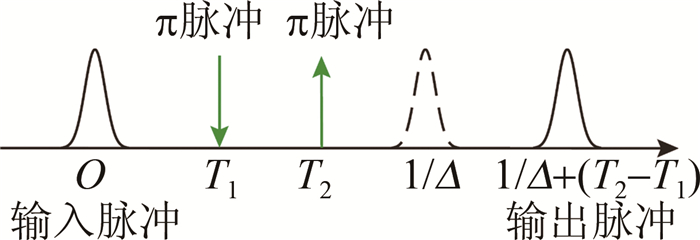
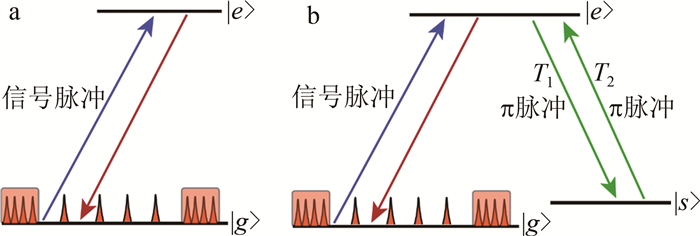
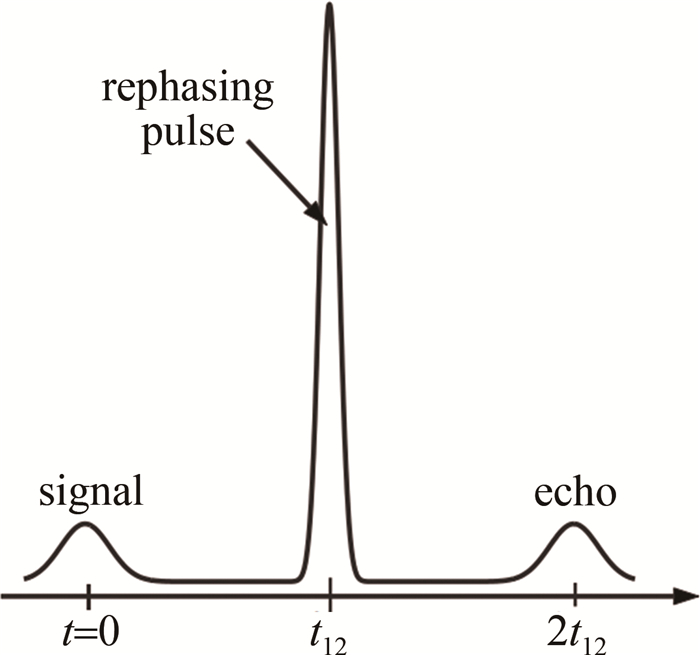
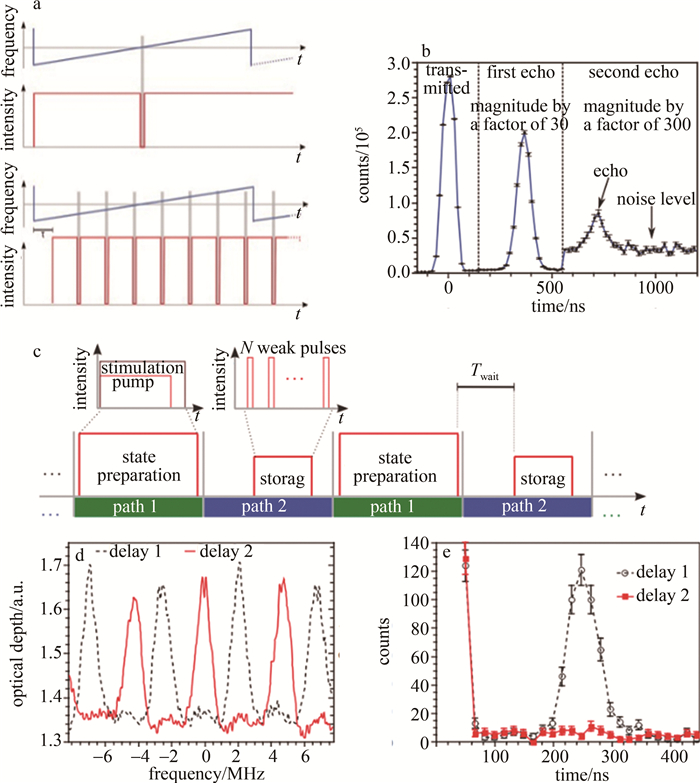
图 6 双脉冲回波示意图[24]
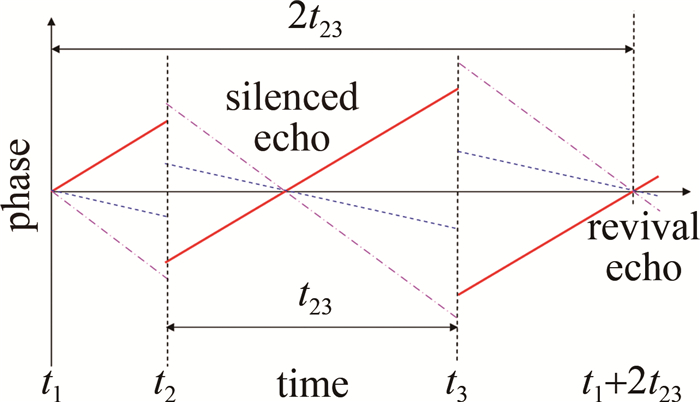
图 7 ROSE协议示意图[27]
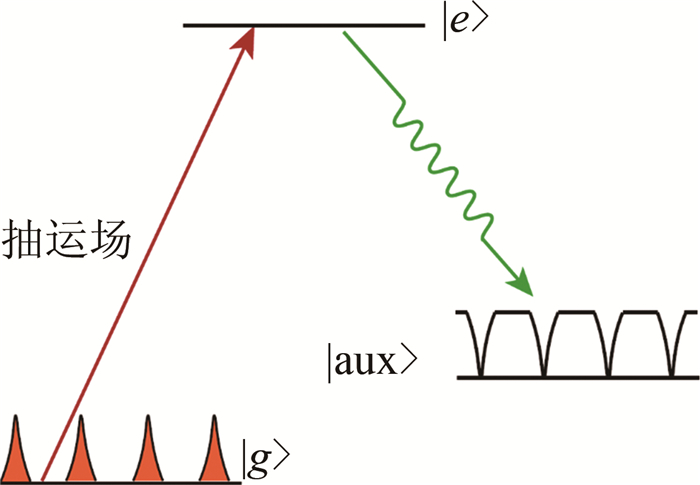
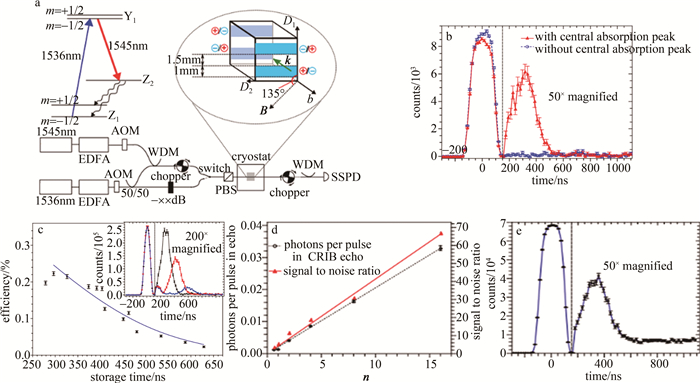
图 8 CRIB协议存储实验图[33]
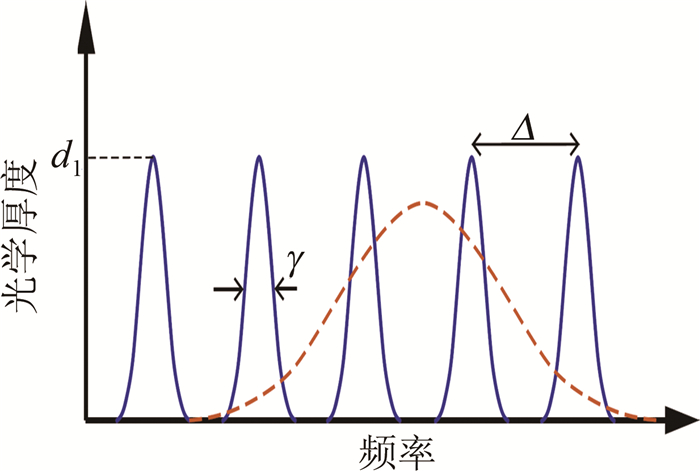
图 9 AFC存储实验图[35]
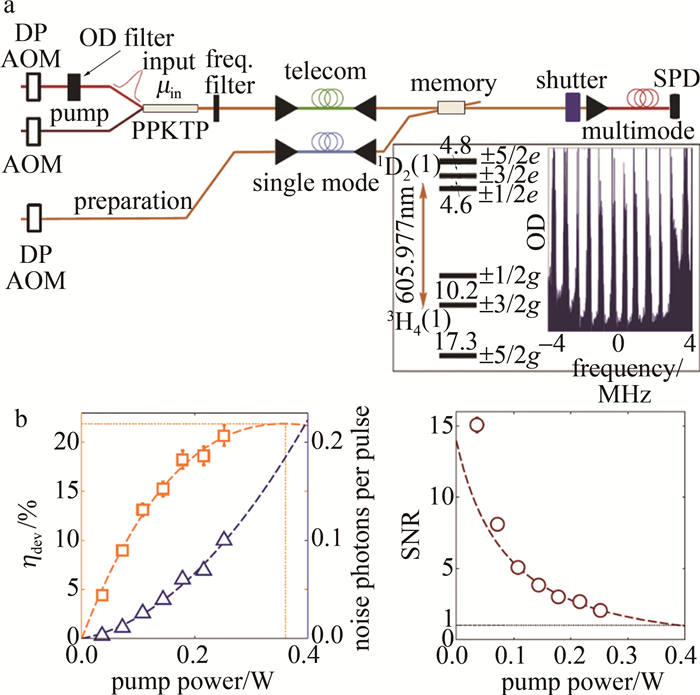
图 10 频率上转换存储实验装置及特性图[36]
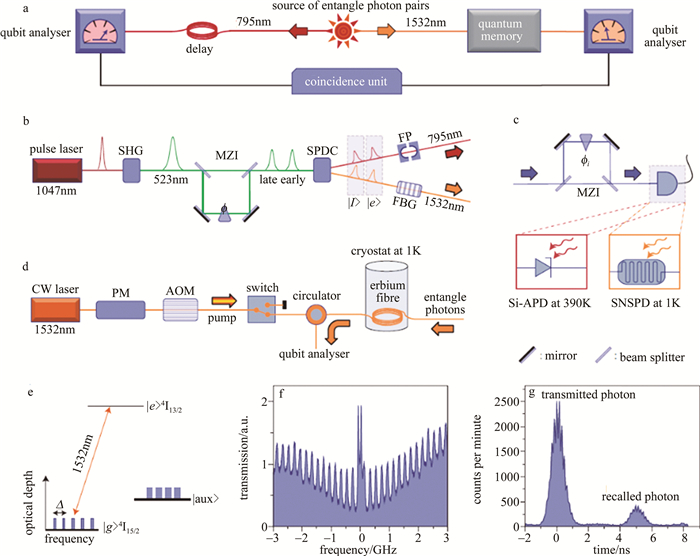
图 11 掺铒光纤存储实验装置及测量结果图[37]
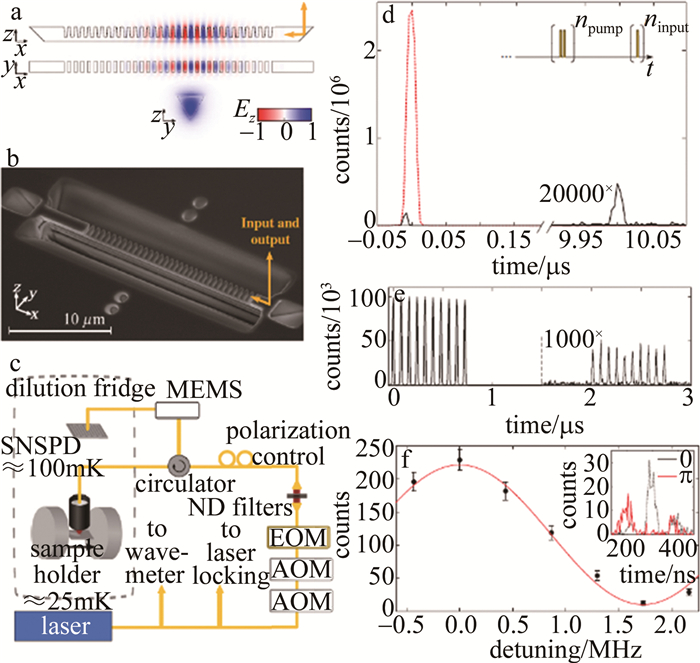
图 12 片上存储实验装置及测量结果图[41]
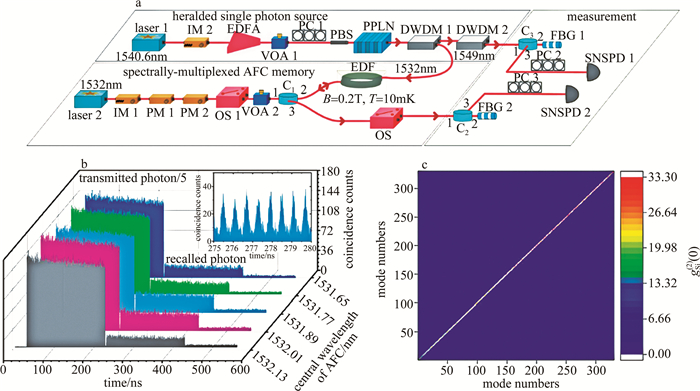
图 13 通信波段多路复用的宽带单光子存储实验装置及测量结果图[44]
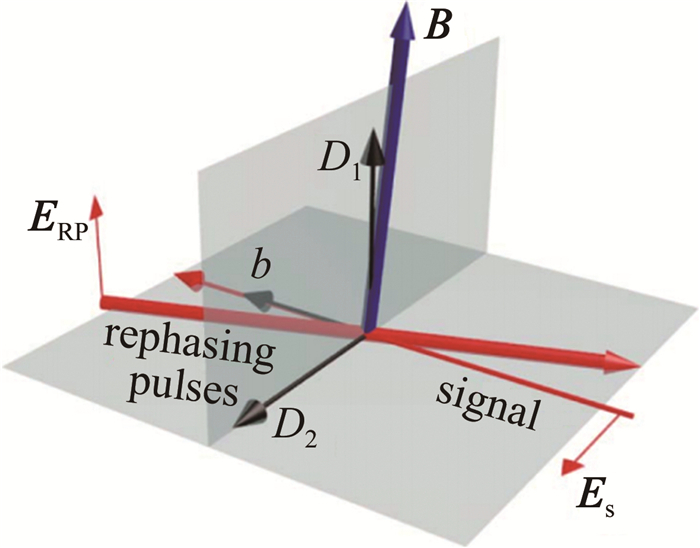
图 14 ROSE实验中磁场、光束及其偏振方向[46]
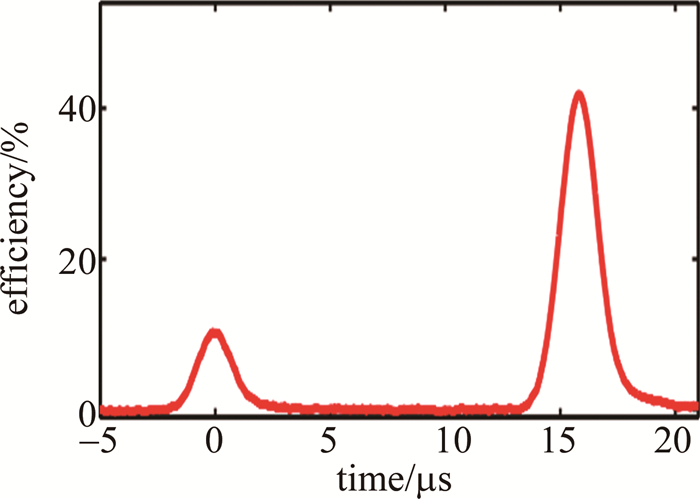
图 15 ROSE回波及其效率[46]
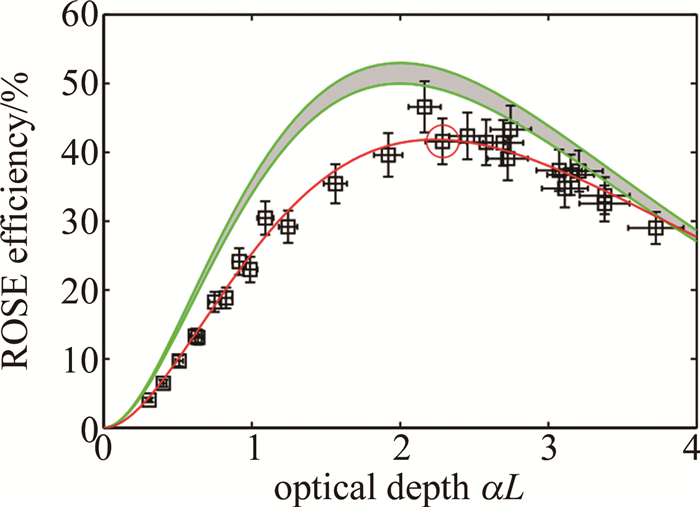
图 16 ROSE效率与光学厚度的函数曲线[46]
-
[1] ZHONG H S, WANG H, DENG Y HAO, et al. Quantum computational advantage using photons[J]. Science, 2020, 370(6523): 1460-1463. DOI: 10.1126/science.abe8770
[2] BRIEGEL H J, DVR W, CIRAC J I, et al. Quantum repeaters: The role of imperfect local operations in quantum communication[J]. Physical Review Letters, 1998, 81(26): 5932-5935. DOI: 10.1103/PhysRevLett.81.5932
[3] SPECHT H P, NÖLLEKE C, REISERER A, et al. A single-atom quantum memory[J]. Nature, 2011, 473(7346): 190-193. DOI: 10.1038/nature09997
[4] BLATT R, WINELAND D. Entangled states of trapped atomic ions[J]. Nature, 2008, 453(7198): 1008-1015. DOI: 10.1038/nature07125
[5] GREZES C, JULSGAARD B, KUBO Y, et al. Multimode storage and retrieval of microwave fields in a spin ensemble[J]. Physical Review, 2014, X4(2): 021049. http://hal.upmc.fr/hal-01340124/document
[6] BHASKAR M K, RIEDINGER R, MACHIELSE B, et al. Experimental demonstration of memory enhanced quantum communication[J]. Nature, 2020, 580(7801): 60-64. DOI: 10.1038/s41586-020-2103-5
[7] CHANELIèRE T, MATSUKEVICH D N, JENKINS S D, et al. Sto-rage and retrieval of single photons transmitted between remote quantum memories[J]. Nature, 2005, 438(7069): 833-836. DOI: 10.1038/nature04315
[8] CHOU C W, de RIEDMATTEN H, FELINTO D, et al. Measurement-induced entanglement for excitation stored in remote atomic ensembles[J]. Nature, 2005, 438(7069): 828-832. DOI: 10.1038/nature04353
[9] RADNAEV A G, DUDIN Y O, ZHAO R, et al. A quantum memory with telecom-wavelength conversion[J]. Nature Physics, 2010, 6(11): 894-899. DOI: 10.1038/nphys1773
[10] BAO X H, REINGRUBER A, DIETRICH P, et al. Efficient and long-lived quantum memory with cold atoms inside a ring cavity[J]. Nature Physics, 2012, 8(7): 517-521. DOI: 10.1038/nphys2324
[11] BUSTARD P J, LAUSTEN R, ENGLAND D G, et al. Toward quantum processing in molecules: A THz-bandwidth coherent memory for light[J]. Physical Review Letters, 2013, 111(8): 083901. DOI: 10.1103/PhysRevLett.111.083901
[12] THIEL C W, BÖTTGER T, CONE R L. Rare-earth-doped materials for applications in quantum information storage and signal processing[J]. Journal of Luminescence, 2011, 131(3): 353-361. DOI: 10.1016/j.jlumin.2010.12.015
[13] LIU G, JACQUIER B. Spectroscopic properties of rare earths in optical materials[M]. Beijing: Tsinghua University Press and Springer-Verlag Berlin Heidelberg, 2005: 23-59.
[14] ZHONG M, HEDGES M P, AHLEFELDT R L, et al. Optically addressable nuclear spins in a solid with a six-hour coherence time[J]. Nature, 2015, 517(7533): 177-180. DOI: 10.1038/nature14025
[15] STONEHAM A M. Shapes of inhomogeneously broadened resonance line in solids[J]. Reviews of Modern physics, 1969, 41(1): 82-108. DOI: 10.1103/RevModPhys.41.82
[16] ZHANG X Y, YUAN Ch Zh, WEI Sh H, et al. Rare earth doped solid state quantum memory[J]. Low Temperature Physical Letters, 2019, 41(5): 315-334 (in Chinese).
[17] LONGDELL J J, FRAVAL E, SELLARS M J, et al. Stopped light with storage times greater than one second using electromagnetically induced transparency in a solid[J]. Physical Review Letters, 2005, 95(6): 063601. DOI: 10.1103/PhysRevLett.95.063601
[18] NILSSON M, KRÖLL S. Solid state quantum memory using complete absorption and re-emission of photons by tailored and externally controlled inhomogeneous absorption profiles[J]. Optics Communications, 2005, 247(4/6): 393-403. http://www.sciencedirect.com/science/article/pii/S0030401804012325
[19] TITTEL W, AFZELIUS M, CHANELIéRE T, et al. Photon-echo quantum memory in solid state systems[J]. Laser & Photonics Reviews, 2009, 4(2): 244-267. http://disser.spbu.ru/disser/info_oponenta_{disser___id}_/Sved_opp_Moiseev1.pdf
[20] SANGOUARD N, SIMON C, AFZELIUS M, et al. Analysis of a quantum memory for photons based on controlled reversible inhomogeneous broadening[J]. Physical Review, 2007, A75(3): 032327. http://www.unige.ch/gap/quantum/_media/publications:bib:qmemosangouard.pdf
[21] SAGLAMYUREK E. Broadband waveguide quantum memory for quantum communication[D]. Calgary, Canada: University of Calgary, 2013: 35.
[22] AFZELIUS M, SIMON C, de RIEDMATTEN H, et al. Multimode quantum memory based on atomic frequency combs[J]. Physical Review, 2009, A79(5): 052329. http://cms.unige.ch/gap/optics/wiki/_media/publications:bib:afc.pdf
[23] HEDGES M P, LONGDELL J J, LI Y, et al. Efficient quantum memory for light[J]. Nature, 2010, 465(7301): 1052-1056. DOI: 10.1038/nature09081
[24] RUGGIERO J, LE GOUËT J L, SIMON C, et al. Why the two-pulse photon echo is not a good quantum memory protocol[J]. Physical Review, 2009, A79(5): 053851. http://www.onacademic.com/detail/journal_1000037059941010_8ef0.html
[25] SANGOUARD N, SIMON C, MINÁŘ J, et al. Impossibility of faithfully storing single photons with the three-pulse photon echo[J]. Physical Review, 2010, A81(6): 062333. http://www.arxiv.org/pdf/1002.5022.pdf
[26] LEDINGHAM P M, NAYLOR W R, LONGDELL J J, et al. Nonclassical photon streams using rephased amplified spontaneous emission[J]. Physical Review, 2010, A81(1): 012301. http://www.researchgate.net/profile/Patrick_Ledingham/publication/45858520_Non-classical_photon_streams_using_rephased_amplified_spontaneous_emission/links/00b7d52ebaef6e523e000000
[27] DAMON V, BONAROTA M, LOUCHET-CHAUVET A, et al. Revival of silenced echo and quantum memory for light[J]. New Journal of Physics, 2011, 13(9): 093031. DOI: 10.1088/1367-2630/13/9/093031
[28] MEIXNER A J, JEFFERSON C M, MAcFARLANE R M. Measurement of the Stark effect with subhomogeneous linewidth resolution in Eu3+∶YAlO3 with the use of photon-echo modulation[J]. Physical Review, 1992, B46(10): 5912-5916. http://www.ncbi.nlm.nih.gov/pubmed/10002273
[29] CHANELIÈRE T, RUGGIERO J, GOUËT J L L, et al. Tm3+∶Y2O3 investigated for a quantum light storage application[J]. Physical Review, 2008, B77(24): 245127.
[30] MOISEEV S A, KRÖLL S. Complete reconstruction of the quantum state of a single-photon wave packet absorbed by a doppler-broadened transition[J]. Physical Review Letters, 2001, 87(17): 173601. DOI: 10.1103/PhysRevLett.87.173601
[31] KRAUS B, TITTEL W, GISIN N, et al. Quantum memory for nonstationary light fields based on controlled reversible inhomogeneous broadening[J]. Physical Review, 2006, A73(2): 020302. http://core.ac.uk/download/pdf/2660191.pdf
[32] ALEXANDER A L, LONGDELL J J, SELLARS M J, et al. Photon echoes produced by switching electric fields[J]. Physical Review Letters, 2006, 96(4): 043602. DOI: 10.1103/PhysRevLett.96.043602
[33] LAURITZEN B, MINÁŘ J, de RIEDMATTEN H, et al. Telecommunication-wavelength solid-state memory at the single photon level[J]. Physical Review Letters, 2010, 104(8): 080502. DOI: 10.1103/PhysRevLett.104.080502
[34] LAURITZEN B, HASTINGS-SIMON S R, DE RIEDMATTEN H, et al. State preparation by optical pumping in erbium-doped solids using stimulated emission and spin mixing[J]. Physical Review, 2008, A78(4): 043402. http://www.gap-optique.unige.ch/wiki/_media/publications:bib:physreva_78_043402.pdf
[35] LAURITZEN B, MINÁŘ J, DE RIEDMATTEN, et al. Approaches for a quantum memory at telecommunication wavelengths[J]. Physical Review, 2011, A83(1): 012318. http://www.unige.ch/gap/quantum/_media/publications:bib:lauritzen2011pra.pdf
[36] MARING N, KUTLUER K, COHEN J, et al. Storage of up-converted telecom photons in a doped crystal[J]. New Journal of Physics, 2014, 16(11): 113021. DOI: 10.1088/1367-2630/16/11/113021
[37] SAGLAMYUREK E, JIN J, VERMA V B, et al. Quantum storage of entangled telecom-wavelength photons in an erbium-doped optical fibre[J]. Nature Photonics, 2015, 9(2): 83-87. DOI: 10.1038/nphoton.2014.311
[38] JIN J, SAGLAMYUREK E, PUIGIBERT M, et al. Telecom-wavelength atomic quantum memory in optical fiber for heralded polarization qubits[J]. Physical Review Letters, 2015, 115(14): 140501. DOI: 10.1103/PhysRevLett.115.140501
[39] SAGLAMYUREK E, PUIGIBERT M L G, ZHOU Q, et al. A multiplexed light-matter interface for fibre-based quantum networks[J]. Nature Communications, 2016, 7: 11202. DOI: 10.1038/ncomms11202
[40] ASKARANI M F, PUIGIBERT M L G, LUTZ T, et al. Storage and reemission of heralded telecommunication-wavelength photons using a crystal waveguide[J]. Physical Review Applied, 2019, 11(5): 054056. DOI: 10.1103/PhysRevApplied.11.054056
[41] CRAICIU I, LEI M, ROCHMAN J, et al. Nanophotonic quantum storage at telecommunication wavelength[J]. Physical Review Applied, 2019, 12(2): 024062. DOI: 10.1103/PhysRevApplied.12.024062
[42] PUIGIBERT M L G, ASKARANI M F, DAVIDSON J H, et al. Entanglement and nonlocality between disparate solid-state quantum memories mediated by photons[J]. Physical Review Research, 2020, 2(1): 013039. DOI: 10.1103/PhysRevResearch.2.013039
[43] CRAICIU I, LEI M, ROCHMAN J, et al. Multifunctional on-chip storage at telecommunication wavelength for quantum networks[J]. Optica, 2021, 8(1): 114-121. DOI: 10.1364/OPTICA.412211
[44] WEI Sh H, JING B, ZHANG X Y, et al. Multiplexed and broadband quantum storage of single-photons at telecom C-band[C]//CLEO-QELS Fundamental Science. Washington DC, USA: Optical Society of America, 2021: FM4M. 2.
[45] XI Q, WEI Sh H, YUAN C Z, et al. Experimental observation of coherent interaction between laser and erbium ions ensemble doped in fiber at sub 10mK[J]. Science China Information Sciences, 2020, 63(8): 180505. DOI: 10.1007/s11432-020-2954-5
[46] DAJCZGEWAND J, LE GOUËT J L, LOUCHET-CHAUVET A, et al. Large efficiency at telecom wavelength for optical quantum memories[J]. Optics Letters, 2014, 39(9): 2711-2714. DOI: 10.1364/OL.39.002711
[47] MAcFARLANE R M, HARRIS T L, SAN Y, et al. Measurement of photon echoes at 1.5μm in Er3+∶Y2SiO5 using a diode laser and amplifier[C]//Quantum Electronics and Laser Science Conference. New York, USA: IEEE, 1997: QTuE24.
[48] BÖTTGER T, THIEL C W, CONE R L, et al. Effects of magnetic field orientation on optical decoherence in Er3+∶Y2SiO5[J]. Physical Review, 2009, B79(11): 115104. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=VIRT04000009000003000103000001&idtype=cvips&gifs=Yes
[49] BÖTTGER T, SUN Y, THIEL C W, et al. Spectroscopy and dynamics of Er3+∶Y2SiO5 at 1.5μm[J]. Physical Review, 2006, B74(7): 075107. http://www.zhangqiaokeyan.com/academic-journal-foreign_other_thesis/0204112079447.html
[50] SUN Y, BÖTTGER T, THIEL C W, et al. Magnetic g tensors for the 4I15/2 and 4I13/2 states of Er3+∶Y2SiO5[J]. Physical Review, 2008, B77(8): 085124. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=PRBMDO000077000008085124000001&idtype=cvips&gifs=Yes
[51] BÖTTGER T, THIEL C W, SUN Y, et al. Optical decoherence and spectral diffusion at 1.5μm in Er3+∶Y2SiO5 versus magnetic field, temperature, and Er3+ concentration[J]. Physical Review, 2006, B73(7): 075101. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=PRBMDO000073000007075101000001&idtype=cvips&gifs=Yes
[52] DUAN L M, LUKIN M D, CIRAC J I, et al. Long-distance quantum communication with atomic ensembles and linear optics[J]. Nature, 2001, 414(6862): 413-418. DOI: 10.1038/35106500
[53] WALLUCKS A, MARINKOVIĆ I, HENSEN B, et al. A quantum memory at telecom wavelengths[J]. Nature Physics, 2020, 16(7): 772-777. DOI: 10.1038/s41567-020-0891-z
[54] MANENTI R, KOCKUM A F, PATTERSON A, et al. Circuit quantum acoustodynamics with surface acoustic waves[J]. Nature Communications, 2017, 8(1): 975. DOI: 10.1038/s41467-017-01063-9
[55] BIENFAIT A, SATZINGER K J, ZHONG Y P, et al. Phonon-mediated quantum state transfer and remote qubit entanglement[J]. Science, 2019, 364: 368-371. DOI: 10.1126/science.aaw8415
[56] SIMON C. Towards a global quantum network[J]. Nature Photonics, 2017, 11(11): 678-680. DOI: 10.1038/s41566-017-0032-0
[57] YIN H L, CHEN T Y, YU Z W, et al. Measurement-device-independent quantum key distribution over a 404km optical fiber[J]. Physical Review Letters, 2016, 117(19): 190501. DOI: 10.1103/PhysRevLett.117.190501
[58] URSIN R, JENNEWEIN T, KOFLER J, et al. Space-quest, experiments with quantum entanglement in space[J]. Europhysics News, 2009, 40(3): 26-29. DOI: 10.1051/epn/2009503




 下载:
下载: